黑马《数据结构与算法2023版》正式发布
有人的地方就有江湖。
在“程序开发”的江湖之中,各种技术流派风起云涌,变幻莫测,每一位IT侠客,对“技术秘籍”的追求和探索也从未停止过。
要论开发技术哪家强,可谓众说纷纭。但长久以来,确有一技,堪称技术江湖的“易筋经”,略知一二的人很多,出类拔萃、登峰造极的人很少...... 江湖人称——数据结构与算法。
曾有人说,这个东西,如果你不去学,可能一辈子都感受不到它的好。但一旦掌握,就会被它的强大威力所折服。
它是程序员内功体现的重要标准之一;
它是大厂必考的内容,
面试的敲门砖、职场晋升的加速器;
它是许多计算机新行业的重要基石;
它能帮我们解决日常开发中的性能问题;
它能帮助我们理解源码背后的设计思想;
它是底层开发的重要一环,
保证底层系统的稳定性和高效性;
......
总结来说,从功利角度,它是大厂必考,你不可避免,从长远角度,它将决定你的技术上限。
一旦拿下了数据结构与算法,就如同站在巨人的肩膀上,在开发江湖占有一席之地。所以你说,数据结构与算法重不重要?该不该学?
黑马2023年重磅巨作 新版《数据结构与算法》正式发布 3大篇章,超90小时,全部免费

秘籍虽香,但修炼甚难。很多同学都曾被枯燥的数学定义、复杂的理论、难懂的公式劝退过。其实,学不会主要是因为方法不对、教材不对。
针对这些痛点,黑马替你出手了!
经过详细的前期调研,潜心研发,本套教程讲练结合,帮助大家把原本分散的知识融会贯通,另外还将算法理论与实践并重,帮助大家加固对高级算法知识的理解和掌握。
更重要的是,跟着黑马老师的步骤,学到的不仅仅是知识和技术,还能沉浸式领略满老师从更高的算法维度,思考、解决开发问题的方式,思维认知得到巨大提升,达到青出于蓝的效果。
适用人群
· 想入门数据结构与算法的同学;
· 已经工作,想晋升涨薪的同学;
· 金三银四,想跳槽突破的同学;
· 挑战自我,想进阶高级开发的同学。





△ 评论来源B站(如侵删)
独门亮点
1. 内容全面
涉及数据结构与算法的各个方面,包括数组、链表、递归、队列、栈、堆、二叉树、查找算法、排序算法、回溯、贪心、分治、动态规划等等。
2. 深入浅出
重点内容,加长篇幅讲解;难点内容,独创动画辅助理解;强化算法思维等深度内容。
3. 顺序合理
正课与题目交替讲解,更为科学;精心设计讲解顺序,重点知识都有前置铺垫。
详情目录
第一章
001-二分查找-算法描述
002-算法实现
003-问题1-循环条件
004-问题2-中间索引
005-问题3-比较符号
006-改动版
007-如何衡量算法好坏-1
008-如何衡量算法好坏-2
009-时间复杂度-大O表示法-1
010-时间复杂度-大O表示法-2
011-如何衡量算法好坏-3
012-二分查找-平衡版
013-Java版
014-LeftRightmost
015-LeftRightmost-返回值
016-LeftRightmost-应用
017-e01-二分查找
017-e02-搜索插入位置
017-e03-搜索开始结束位置
018-数组-概述
019-动态数组-介绍
020-插入
021-遍历
022-删除
023-扩容
024-二维数组
025-数组-缓存与局部性原理
026-链表-概述
027-单向链表-addFirst
028-遍历
029-addLast
030-get
031-insert
032-removeFirst
033-remove
034-带哨兵-1
035-带哨兵-2
036-双向链表-带哨兵-1
037-带哨兵-2
038-双向环形链表-带哨兵-1
039-带哨兵-2
040-链表-递归遍历
041-递归-定义
042-阶乘
043-反向打印字符串
044-e03-二分查找
044-e04-冒泡排序1
044-e04-冒泡排序2
044-e05-插入排序1
044-e05-插入排序2
045-多路递归-斐波那契
046-时间复杂度
047-兔子问题
048-青蛙跳台阶
049-递归-优化-记忆法
050-爆栈问题
051-尾调用与尾递归
052-尾递归避免爆栈
053-主定理求时间复杂度-1
054-主定理求时间复杂度-2
055-展开求时间复杂度-1
056-展开求时间复杂度-2
057-多路递归-e02-汉诺塔1
057-e02-汉诺塔2
057-e03-杨辉三角1
057-e03-杨辉三角2
057-e03-杨辉三角3
058-链表-e01-反转单向链表1
058-e01-反转单向链表2
058-e01-反转单向链表3-递归
058-e01-反转单向链表4
058-e01-反转单向链表5
058-e02-根据值删除节点1
058-e02-根据值删除节点2-递归
058-e03-删除倒数节点1-递归
058-e03-删除倒数节点2
058-e04-有序链表去重1
058-e04-有序链表去重2-递归
058-e05-有序链表去重1-递归
058-e05-有序链表去重2
058-e06-合并有序链表1
058-e06-合并有序链表2
058-e07-合并多个有序链表
058-e08-查找链表中间节点
058-e09-判断回文链表1
058-e09-判断回文链表2
058-e10-判环算法1
058-链表-e10-判环算法2
059-数组-e01-合并有序数组1
059-数组-e01-合并有序数组2
060-队列-链表实现-1
061-队列-链表实现-2
062-队列-环形数组实现-方法1-1
063-方法1-2
064-方法2
065-方法3-1
066-方法3-2
067-方法3-3
068-方法3-4
069-队列-e01-二叉树层序遍历1
069-队列-e01-二叉树层序遍历2
070-栈-链表实现
071-栈-数组实现
072-栈-e01-有效的括号
072-e02-后缀表达式求值
072-e03-中缀表达式转后缀1
072-e03-中缀表达式转后缀2
072-e03-中缀表达式转后缀3
072-e04-双栈模拟队列
072-e05-单队列模拟栈
073-双端队列-链表实现-1
074-链表实现-2
075-数组实现-1
076-数组实现-2
077-数组实现-3
078-双端队列-e01-二叉树Z字层序遍历
079-优先级队列-无序数组实现
080-有序数组实现
081-堆实现-1
082-堆实现-2
083-堆实现-3
084-优先级队列-e01-合并多个有序链表1
084-优先级队列-e01-合并多个有序链表2
085-阻塞队列-问题提出
086-单锁实现-1
087-单锁实现-2
088-单锁实现-3
089-单锁实现-4
090-单锁实现-5
091-双锁实现-1
092-双锁实现-2
093-双锁实现-3
094-双锁实现-4
095-双锁实现-5
096-堆-heapify-1
097-heapify-2
098-heapify-3
099-增-删-替换
100-堆-e01-堆排序
100-e02-求数组第k大元素
100-e03-求数据流第k大元素
100-e04-求数据流中位数1
100-e04-求数据流中位数2
100-e04-求数据流中位数3
以上仅是冰山一角 更多高级知识持续更新中……
时值招聘黄金期,如何独领风骚?
本套《数据结构与算法》高级教程
恰是你四两拨千斤的得力法宝
有同学可能会惊叹:
还没更新完目录就这么长
等学完孩子都会敲 "Hello World" 了
如果你每天学一点,十天就学了十点
坚持一个月,你会发现你已经学了一个月
(废话文学,手动狗头)
第一章部分内容已上传
后续课程正在加急制作中
学习上乘武功这事,切不可操之过急
跟着老师的步骤,循序渐进即可
相关文章:

黑马《数据结构与算法2023版》正式发布
有人的地方就有江湖。 在“程序开发”的江湖之中,各种技术流派风起云涌,变幻莫测,每一位IT侠客,对“技术秘籍”的追求和探索也从未停止过。 要论开发技术哪家强,可谓众说纷纭。但长久以来,确有一技&#…...
Spring的创建和使用
目录 创建Spring项目 步骤 1)使用Maven的方式创建Spring项目 2)添加Spring依赖 3)创建启动类 存Bean对象 1.创建Bean对象 2.将Bean注册到Spring中 取Bean对象并使用 步骤 1.先得到Spring上下文对象 2.从Spring中获取Bean对象 3.使用Bean ApplicationContext VS Bea…...
如何实现外网跨网远程控制内网计算机?快解析来解决
远程控制,是指管理人员在异地通过计算机网络异地拨号或双方都接入Internet等手段,连通需被控制的计算机,将被控计算机的桌面环境显示到自己的计算机上,通过本地计算机对远方计算机进行配置、软件安装程序、修改等工作。通俗来讲&a…...

【跟着ChatGPT学深度学习】ChatGPT教我文本分类
【跟着ChatGPT学深度学习】ChatGPT教我文本分类 ChatGPT既然无所不能,我为啥不干脆拜他为师,直接向他学习,岂不是妙哉。说干就干,我马上就让ChatGPT给我生成了一段文本分类的代码,不看不知道,一看吓一跳&am…...

IM即时通讯架构技术:可靠性、有序性、弱网优化等
消息的可靠性是IM系统的典型技术指标,对于用户来说,消息能不能被可靠送达(不丢消息),是使用这套IM的信任前提。 换句话说,如果这套IM系统不能保证不丢消息,那相当于发送的每一条消息都有被丢失的…...

【算法】三道算法题两道难度中等一道困难
算法目录只出现一次的数字(中等难度)java解答参考二叉树的层序遍历(难度中等)java 解答参考给表达式添加运算符(比较困难)java解答参考大家好,我是小冷。 上一篇是算法题目 接下来继续看下算法题…...
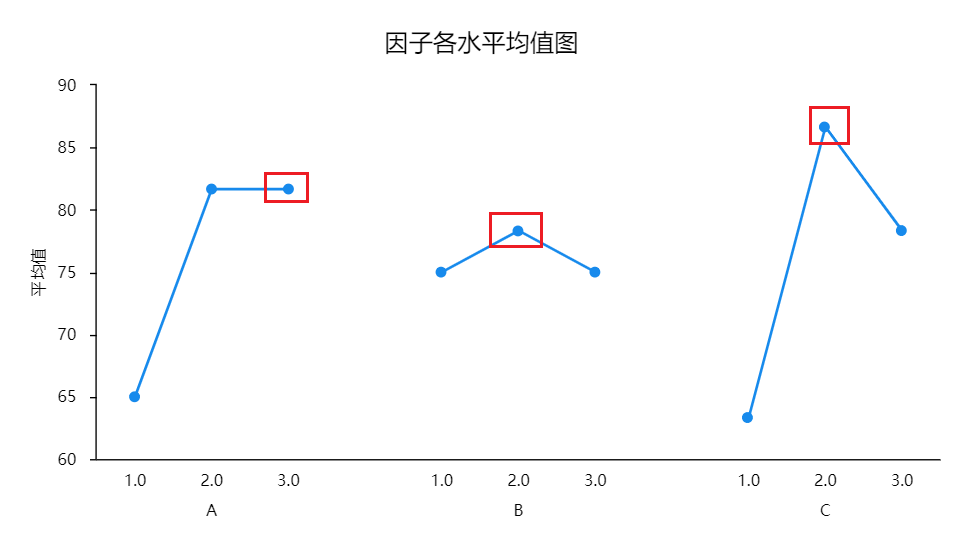
正交实验与极差分析
正交试验极差分析流程如下图: 正交试验说明 正交试验是研究多因素试验的设计方法。对于多因素、多水平的实验要求,如果每个因素的每个水平都要进行试验,这样就会耗费大量的人力和时间,正交试验可以选择出具有代表性的少数试验进行…...
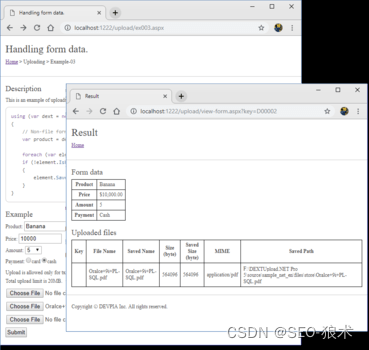
DEXTUpload .NET增强的上传速度和可靠性
DEXTUpload .NET增强的上传速度和可靠性 DEXTUpload.NET Pro托管在Windows操作系统上的Internet Information Server(IIS)上,服务器端组件基于HTTP协议,支持从web浏览器到web服务器的文件上载。它也可以在ASP.NET服务器应用程序平台开发的任何网站上使用…...
)
SkyWalking 将方法加入追踪链路(@Trace)
SkyWalking8 自定义链路追踪@Trace 自定义链路,需要依赖skywalking官方提供的apm-toolkit-trace包.在pom.xml的dependencies中添加如下依赖: <dependency><groupId>org.apache.skywalking</groupId><artifactId>apm-toolkit-trace</artifactId>&…...
MySQL Administrator定时备份MySQL数据库
1、下载并安装软件mysql-gui-tools-5.0-r17-win32.exe 2、将汉化包zh_CN文件夹拷贝到软件安装目录 3、菜单中打开MySql Adminstrator,见下图,初次打开无服务实例。 点击已存储连接右侧按钮①,打开下图对话框。点击“新连接”按钮ÿ…...

Kubernetes入门教程 --- 使用二进制安装
Kubernetes入门教程 --- 使用二进制安装1. Introduction1.1 架构图1.2 关键字介绍1.3 简述2. 使用Kubeadm Install2.1 申请三个虚拟环境2.2 准备安装环境2.3 配置yum源2.4 安装Docker2.4.1 配置docker加速器并修改成k8s驱动2.5 时间同步2.6 安装组件3. 基础知识3.1 Pod3.2 控制…...

深度学习模型压缩方法概述
一,模型压缩技术概述 1.1,模型压缩问题定义 因为嵌入式设备的算力和内存有限,因此深度学习模型需要经过模型压缩后,方才能部署到嵌入式设备上。 模型压缩问题的定义可以从 3 角度出发: 模型压缩的收益: 计算: 减少浮点运算量(FLOPs),降低延迟(Latency)存储: 减少内…...

《NFL橄榄球》:坦帕湾海盗·橄榄1号位
坦帕湾海盗(英语:Tampa Bay Buccaneers)是一支位于佛罗里达州的坦帕湾职业美式橄榄球球队。他们是全国橄榄球联盟的南区其中一支球队。在1976年,与西雅图海鹰成为NFL的球队。球队在最初的两个球季连败26场,在二十世纪七…...
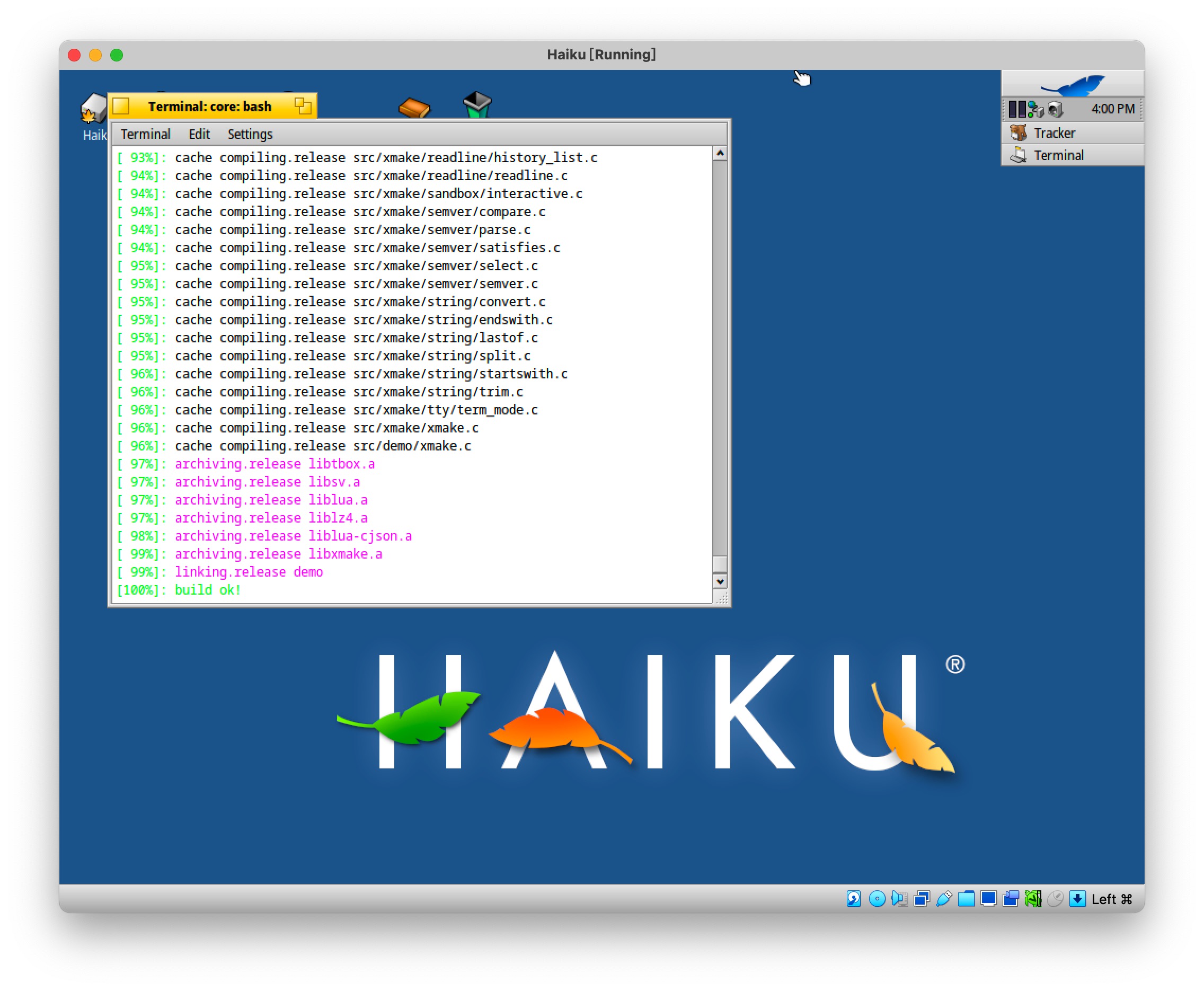
Xmake v2.7.7 发布,支持 Haiku 平台,改进 API 检测和 C++ Modules 支持
layout: post.cn title: “Xmake v2.7.7 发布,支持 Haiku 平台,改进 API 检测和 C Modules 支持” tags: xmake lua C/C package modules haiku cmodules categories: xmake Xmake 是一个基于 Lua 的轻量级跨平台构建工具。 它非常的轻量,没…...

苹果ios签名证书的生成方法
在使用hbuilderx打包uniapp或html5应用的时候,假如是打包ios应用,是需要ios签名证书,和证书profile文件的,这个证书要求是p12格式的证书,profile文件又叫描述文件。 这两个文件,需要在苹果开发者中心生成&…...

c++开发配置常用网站记录
1.ubuntu 镜像源: (1) 清华源:https://mirror.tuna.tsinghua.edu.cn/help/ubuntu/ (2) 阿里源:https://developer.aliyun.com/mirror/ubuntu?spma2c6h.13651102.0.0.3e221b11VuM27s 包含了ubuntu各个版本的source源 2.ubuntu iso镜像下载…...
DC-1 靶场学习
以前写过了,有一些忘了,快速的重温一遍。 DC一共九个靶场,目标一天一个。 文章目录环境配置:信息搜集:漏洞复现:FLAG获取环境配置: 最简单的办法莫过于将kali和DC-1同属为一个nat的网络下。 信…...

oracle 不使用索引深入解析
首先,我们要确定数据库运行在何种优化模式下,相应的参数是:optimizer_mode。缺省的设置应是"choose",即如果对已分析的表查询的话选择CBO,否则选择RBO。如果该参数设为“rule”,则不论表是否分析…...

什么是自助式BI工具,有没有推荐
为什么需要自助式BI? 传统的BI采用的是“业务提报表需求,IT进行开发”的模式。决策管理者和业务人员提出用报表等来展示经营管理数据的需求;接着IT响应需求,进行需求沟通、数据处理加工、报表开发等主体工作;最后决策管…...

如何高效管理自己的时间,可以从这几个方向着手
如果你是上班族,天选打工人,你的绝大多数时间都属于老板,能够自己支配的时间其实并不多,所以你可能察觉不到时间管理的重要性。但如果你是自由职业者或者创业者,想要做出点成绩,那你就需要做好时间管理&…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
