洛谷P1601
题目见:P1601 A+B Problem(高精) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
1. 问题分析
加法计算问题应该和在界面输出“Hello,world!”是一个难度级别,但是问题在于受限于原始数据类型的限制,无法进行大数据的精确的加法运算。即使双精度浮点数计算近似值,最大数差不多是308位数字,超过这个位数也是无法计算的。那这样就有问题了,利用原始的数据类型是无法存储一个任意大的整数的,需要自定义类型和运算和实现。Java中就有这种类型,python的加法也可以实现。那么如果用C++来写的话,应该如何去做呢?(做法很多,美丽的做法也跟多,我只是从个人角度出发来考虑这个问题)
其实想法很简单,我们用数组来表示一个整数,有多少位,数组的长度就设置多少完了。比如存储123.
#include<iostream>
using namespace std;
int main(){int a[3] = {1,2,3};return 0;
}这样以来,我们就可以通过两个数组来表示两个整数,通过两个数组来利用加法的运算规则来进行计算了。
2. 计算步骤
2.1 输入问题
题目输入的是两个整数,我们用什么来接收这两个数字呢?任意长度的,我们可以用字符串来接收这两个整数。
#include<bits\stdc++.h>
using namespace std;
int main(){string a, b;cin >> a;cin >> b;return 0;
}2.2 字符串转化为整数数组
2.2.1 位置关系
我们需要将字符串的最后一位,也就是个位数放置在整数数组的第0个位置,将倒数第二个位置的字符转为整数放置在整数数组的第1个位置,一次类推。
2.2.2 类型转化
字符串(string)实际上是一个字符数组,字符串的每个位置是一个char类型,char类型采用ascii来存储,acsii对于0~9的数字是连续存储的,因此只需要用字符串每个位置的char类型减去字符0既可。
2.2.3 代码实现
#include<bits\stdc++.h>
using namespace std;void str2char_arr(string str, int a[]){int n = str.size();for (int i = n-1; i>=0; i--){a[n-i-1] = str[i] - '0';}
}
void display(int a[], int n, bool reverse){for (int i = 0; i < n; i++){if (reverse == true){cout << a[n-1-i];}else{cout << a[i];}}
}
int main(){string str1, str2;int a[500];int b[500];cin >> str1;cin >> str2;str2char_arr(str1, a);str2char_arr(str2, b);display(a, str1.size(), false);return 0;
}2.3 定义加法运算
加法运算的规则如下:
1. 从左到右依次计算
2. 两个数组的数字对应位置相加,加上上一次的进位(上次进位为上次的和除以10的商),然后对10取余。
注意:可以根据题目中数据的大小约束,设置较大的数组,并且两个数组的大小一致,这样有点浪费空间和时间。后面可以用可变数组来优化。
#include<bits\stdc++.h>
using namespace std;void str2char_arr(string str, int a[]){int n = str.size();for (int i = n-1; i>=0; i--){a[n-i-1] = str[i] - '0';}
}
void display(int a[], int n, bool reverse){for (int i = 0; i < n; i++){if (reverse == true){cout << a[n-1-i];}else{cout << a[i];}}
}void add(int a[], int b[], int c[], int n){int t = 0;for (int i = 0; i < n; i++){t += a[i] + b[i];c[i] = t%10;t /= 10;}
}int main(){string str1, str2;int a[501];int b[501];int c[501];int n = 501;cin >> str1;cin >> str2;memset(a, 0, sizeof(a));memset(b, 0, sizeof(b));str2char_arr(str1, a);str2char_arr(str2, b);add(a, b, c, n);while(c[n-1] == 0 && n > 1){n--;}display(c, n, true);return 0;
}2.4 逆序输出
计算的时候从个位数开始计算,个位数的索引小,所以输出的时候需要逆序输出。另外就是要从第一个不为0的数字输出。
3. 优化
这只是一个初级版本,优化空间很大。
相关文章:

洛谷P1601
题目见:P1601 AB Problem(高精) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 1. 问题分析 加法计算问题应该和在界面输出“Hello,world!”是一个难度级别,但是问题在于受限于原始数据类型的限制,无法进行大数据的精…...

Elasticsearch:使用 LangChain 对话链和 OpenAI 的聊天机器人
在此笔记本中,我们将构建一个聊天机器人,它可以回答有关自定义数据的问题,例如雇主的政策。 聊天机器人使用 LangChain 的 ConversationalRetrievalChain,具有以下功能: 用自然语言回答问题在 Elasticsearch 中运行混…...
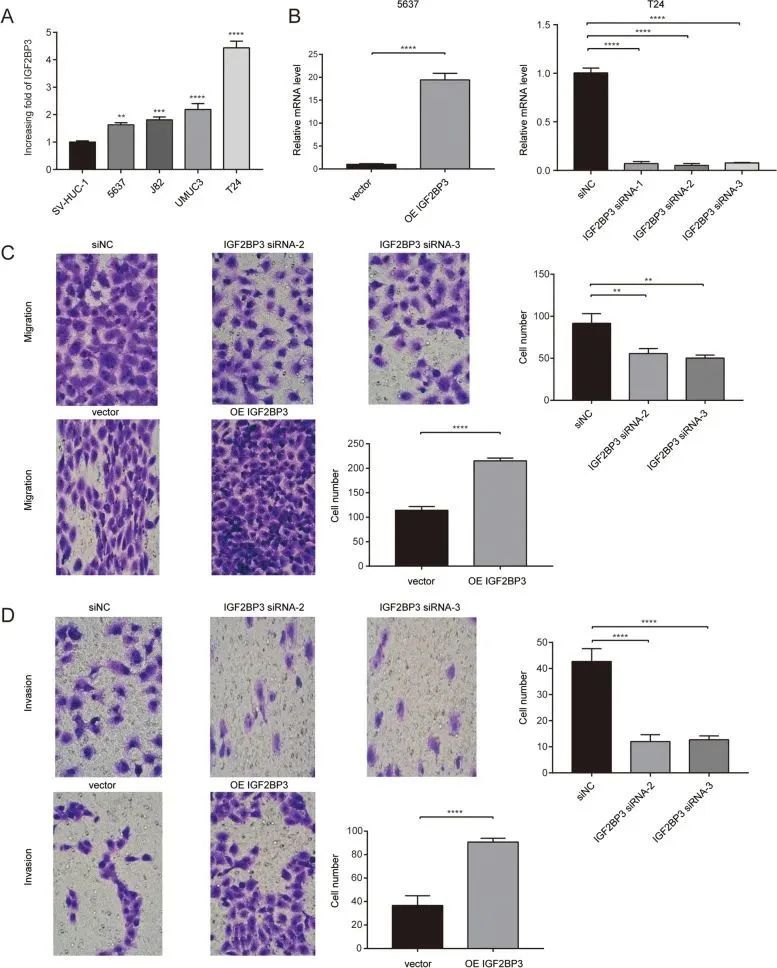
铜死亡+机器学习+WGCNA+分型生信思路
今天给同学们分享一篇单基因泛癌免疫实验生信文章“IGF2BP3 overexpression predicts poor prognosis and correlates with immune infiltration in bladder cancer”,这篇文章于2023年2月3日发表在BMC Cancer期刊上,影响因子为3.8。 膀胱癌是全球最常见…...

GB28181平台简介
产品简介 LiveMedia视频中间件是支持部署到本地服务器或者云服务器的纯软件服务,也提供服务器、GPU一体机全包服务,提供视频设备管理、无插件、跨平台的实时视频、历史回放、语音对讲、设备控制等基础功能,支持视频协议有海康、大华私有协议…...
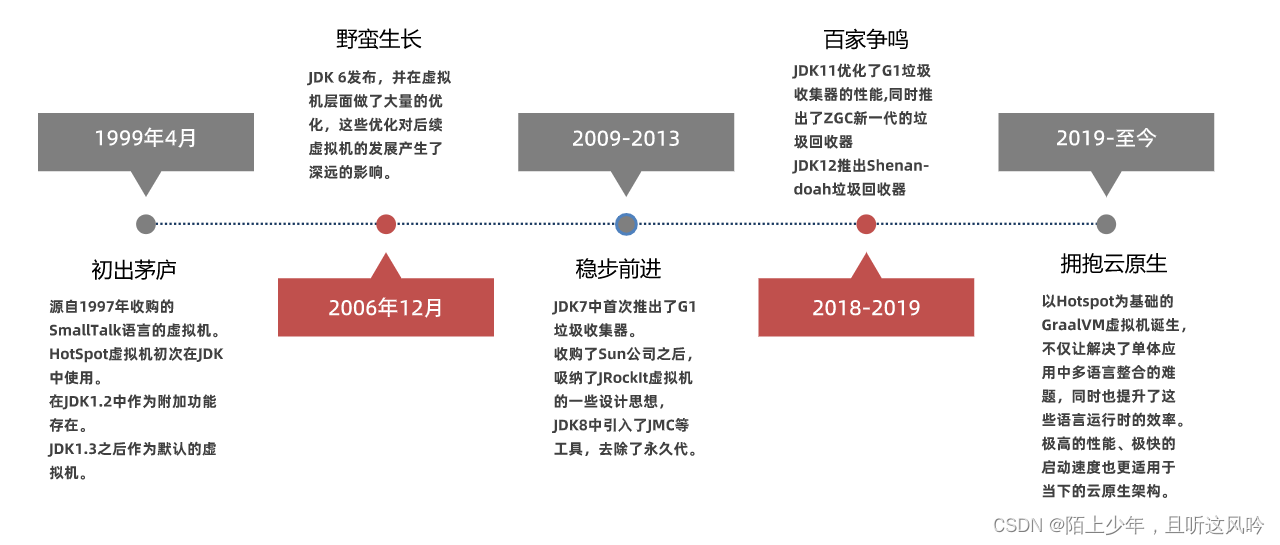
JVM基础:初识JVM
IDE:IntelliJ IDEA 2022.1.3 x64 操作系统:win10 x64 位 家庭版 文章目录 一、JVM是什么?二、JVM有哪些功能?2.1 解释和运行2.2 内存管理2.3 即时编译 三、有哪些常见的JVM?3.1 常见JVM3.2 Java虚拟机规范3.3 HotSpot的…...
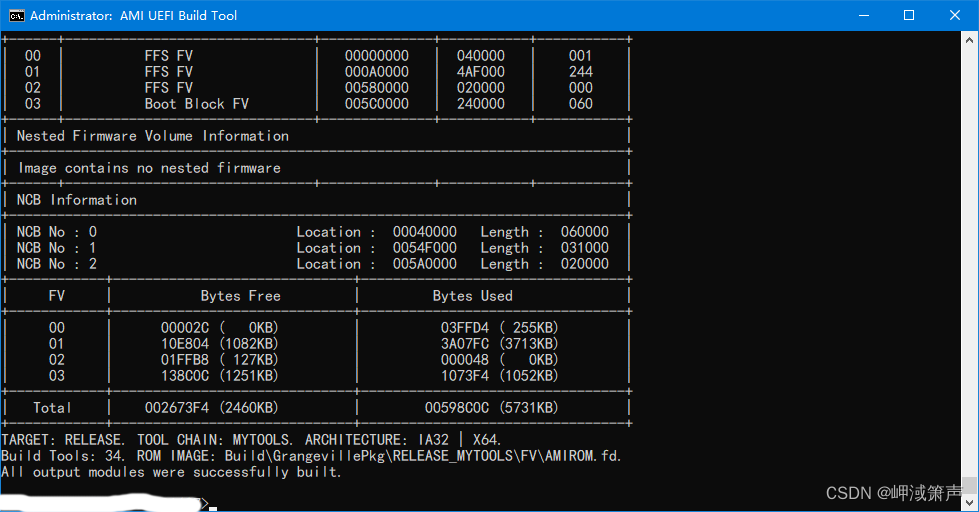
至强服务器BIOS/UEFI驱动开发笔记
至强服务器BIOS/UEFI驱动开发笔记 驱动开发基础Hello UEFI Driver 项目选择项目位置初始化驱动代码文件结构驱动程序入口和基本功能导入AMI工程AMI平台Hello UEFI Driver 编译问题测试结果打印设备列表继续开发`HelloWorldSupported`函数依赖配置使用脚本编译编译测试此DXE驱动…...
Linux:Termius连接本地虚拟机与虚拟机快照
Termius连接本地虚拟机与虚拟机快照 1. Termius连接本地虚拟机2. 虚拟机快照与还原2.1 设置快照以及恢复 附录 1. Termius连接本地虚拟机 ifconfig -a 查看配置 连接成功 2. 虚拟机快照与还原 在学习阶段我们无法避免的可能损坏Linux操作系统。 如果损坏的话,重新…...

高校教务系统登录页面JS分析——四川大学
高校教务系统密码加密逻辑及JS逆向 本文将介绍高校教务系统的密码加密逻辑以及使用JavaScript进行逆向分析的过程。通过本文,你将了解到密码加密的基本概念、常用加密算法以及如何通过逆向分析来破解密码。 本文仅供交流学习,勿用于非法用途。 一、密码加…...
Kafka SASL认证授权(四)认证源码解析
Kafka SASL认证授权(四)认证源码解析。 官网地址:https://kafka.apache.org/ 一、认证流程 在了解kafka网络模型的基础上,了解它的认证流程: ApiVersionsRequest->SaslHandshakeRequest->a series of SASL client and server tokens corresponding to the mechani…...

软件测试学习(一)基础概念、实质、说明书测试、分类、动态黑盒测试
目录 软件测试概念、背景 软件测试员究竟做些什么 大多数软件测试员应该具备的素质 软件测试的实质 完全测试程序是不可能的 测试无法显示潜伏的软件缺陷 并非所有软件缺陷都要修复 软件测试员在产品小组中不受欢迎 术语:精准和准确 产品说明书的测试技术…...

在fastapi中实现异步
在FastAPI应用中使用异步特性可以提高并发性能,但如果您要调用的模型是同步的,可能会导致阻塞。为了实现异步处理,您可以将阻塞的操作委托给线程池或进程池,以便异步执行。 以下是一种基本方法来实现异步处理图片识别任务&#x…...

js数组去重
在JavaScript中,有很多方法可以用来去除数组中的重复项。以下是一些常见的方法: 方法一:使用Set Set是ES6中的新数据类型,它只存储唯一值。因此,我们可以利用这一特性来去重。 let array [1, 2, 3, 2, 1, 4, 3, 5,…...

【前端】根据后端返回的url进行下载并设置文件下载名称
在我们项目当中存储文件是存储到厂商的服务器上的,然后厂商返回一个可以直接下载url地址,但是前端使用这个url下载的时候永远都是保存一个名字,这时候我们就需要设置文件保存的名称, 那么如何实现呢?使用了fet…...

《视觉SLAM十四讲》公式推导(一)
文章目录 CH3 三维空间刚体运动CH3-1 旋转矩阵的推导CH3-2 旋转矩阵是正交矩阵的证明CH3-3 变换矩阵的逆的推导CH3-4 罗德里格斯公式推导 CH3 三维空间刚体运动 CH3-1 旋转矩阵的推导 (1)二维空间中的旋转矩阵 易得 { x ′ ∣ O P ′ ∣ c o s ( θ …...
简单好用的解压缩软件:keka 中文 for mac
Keka是一款功能全面、易于使用的文件压缩和解压缩软件,为Mac用户提供了便捷的文件管理工具。它支持多种压缩格式,具有快速解压和强大的压缩功能,让您能够轻松地处理各种文件压缩需求。 隐私非常重要 安全共享只需设置密码并创建高度加密的文…...

【UE 插件】UE4 虚幻引擎 插件开发(带源码插件打包、无源码插件打包) 有这一篇文章就够了!!!
目录 0 引言1 快速入门1.1 新建插件的前提1.2 创建插件步骤1.3 打包插件 2 无源代码的插件制作3 插件详细介绍3.1 插件的使用方法3.1 UE 预置插件模版3.1.1 空白3.1.2 纯内容3.1.3 编辑器独立窗口3.1.4 编辑器工具栏按钮3.1.5 编辑器模式3.1.6 第三方库3.1.7 蓝图库 3.2 插件中…...
C# CodeFormer 图像修复
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.Drawing; using System.Drawing.Imaging; using System.Windows.Forms;namespace 图像修复 {p…...

Android Studio的笔记--HttpURLConnection使用GET下载zip文件
HttpURLConnection使用GET下载zip文件 http get下载zip文件MainActivity.javaAndroidMainfest.xmlactivity_main.xmllog http get下载zip文件 MainActivity.java 用HttpURLConnection GET方法进行需注意: 1、Android 9及以上版本需要设置这个,否则会有…...
phantom3D模体
phantom是人头模型,分为2D和3D两种,matlab中可直接调用phantom(size)生成2D数据,如图1,而三维需要对应函数文件,下载:3D 图1 2D phantom 3D模体为一个椭球体,只能生成xyz三个方向相同维度的模…...

贪心算法解决批量开票限额的问题
具体问题:批量订单开票 限制:1.开最少的张数 2.每张限额10w # 贪心算法 def split_invoice_by_item(items):items_sorted sorted(items, keylambda x: x.price, reverseTrue)invoices []for item in items_sorted:# 尝试将商品加入已有的发票中added …...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
