《视觉SLAM十四讲》公式推导(一)
文章目录
- CH3 三维空间刚体运动
- CH3-1 旋转矩阵的推导
- CH3-2 旋转矩阵是正交矩阵的证明
- CH3-3 变换矩阵的逆的推导
- CH3-4 罗德里格斯公式推导
CH3 三维空间刚体运动
CH3-1 旋转矩阵的推导
(1)二维空间中的旋转矩阵

易得
{ x ′ = ∣ O P ′ ∣ c o s ( θ + β ) = ∣ O P ∣ ( c o s θ ⋅ c o s β − s i n θ ⋅ s i n β ) = x c o s β − y s i n β y ′ = ∣ O P ′ ∣ s i n ( θ + β ) = ∣ O P ∣ ( s i n θ ⋅ c o s β + c o s θ ⋅ s i n β ) = y c o s β + x s i n β \left\{ \begin{matrix} x'=|OP'|cos(\theta+\beta)=|OP|(cos\theta\cdot cos\beta-sin\theta\cdot sin\beta)=xcos\beta-ysin\beta \\ y'=|OP'|sin(\theta+\beta)=|OP|(sin\theta\cdot cos\beta+cos\theta\cdot sin\beta)=ycos\beta+xsin\beta \end{matrix} \right. {x′=∣OP′∣cos(θ+β)=∣OP∣(cosθ⋅cosβ−sinθ⋅sinβ)=xcosβ−ysinβy′=∣OP′∣sin(θ+β)=∣OP∣(sinθ⋅cosβ+cosθ⋅sinβ)=ycosβ+xsinβ
写为矩阵形式即
[ x ′ y ′ ] = [ c o s β − s i n β s i n β c o s β ] [ x y ] \left[\begin{array}{l} x' \\ y' \end{array}\right]= \left[\begin{array}{l} cos\beta & -sin\beta \\ sin\beta & cos\beta \end{array}\right] \left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[cosβsinβ−sinβcosβ][xy]
(2)三维空间中的旋转矩阵
以绕 z z z 轴旋转为例:

将向量投影到 X-Y 平面,类似的有
{ x ′ = x c o s β − y s i n β y ′ = y c o s β + x s i n β z ′ = z (3-1-1) \left\{ \begin{matrix} x'=xcos\beta-ysin\beta \\ y'=ycos\beta+xsin\beta \\ z'=z \end{matrix} \right. \tag{3-1-1} ⎩ ⎨ ⎧x′=xcosβ−ysinβy′=ycosβ+xsinβz′=z(3-1-1)
写成矩阵形式
[ x ′ y ′ z ′ ] = [ c o s β − s i n β 0 s i n β c o s β 0 0 0 1 ] [ x y z ] (3-1-2) \left[\begin{array}{l} x' \\ y' \\ z' \end{array}\right]= \left[\begin{array}{l} cos\beta & -sin\beta & 0\\ sin\beta & cos\beta & 0\\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{l} x \\ y \\ z \end{array}\right] \tag{3-1-2} x′y′z′ = cosβsinβ0−sinβcosβ0001 xyz (3-1-2)
记为
a ′ = R a (3-1-3) \boldsymbol{a^{\prime}}=\boldsymbol{Ra} \tag{3-1-3} a′=Ra(3-1-3)
将式中 β \beta β 改为 − β -\beta −β,来表示向量 OP’ 顺时针旋转 − β -\beta −β 角度后,回到 OP 的过程,此时
[ x y z ] = [ c o s β s i n β 0 − s i n β c o s β 0 0 0 1 ] [ x ′ y ′ z ′ ] (3-1-4) \left[\begin{array}{l} x \\ y \\ z \end{array}\right]= \left[\begin{array}{l} cos\beta & sin\beta & 0\\ -sin\beta & cos\beta & 0\\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{l} x' \\ y' \\ z' \end{array}\right] \tag{3-1-4} xyz = cosβ−sinβ0sinβcosβ0001 x′y′z′ (3-1-4)
可以看出
a = R T a ′ (3-1-5) \boldsymbol{a}=\boldsymbol{R^Ta'} \tag{3-1-5} a=RTa′(3-1-5)
由于 R R R 是正交矩阵,也即
a = R − 1 a ′ (3-1-6) \boldsymbol{a}=\boldsymbol{R^{-1}a'} \tag{3-1-6} a=R−1a′(3-1-6)
也就是说, R − 1 \boldsymbol{R^{-1}} R−1 表示向量经反方向旋转回到原向量的过程。
当然,也可以单纯从数学角度推导,将式(3-1-3) 两端分别左乘 R − 1 \boldsymbol{R^{-1}} R−1,同样可以得到式 (3-1-5)。
CH3-2 旋转矩阵是正交矩阵的证明
(1)只需证明 R R T = I \boldsymbol{RR^T=I} RRT=I 即证明 R T = R − 1 \boldsymbol{R^T = R^{-1}} RT=R−1 即可。
(2)分块矩阵转置:先对整体进行转置,再对每一个分块进行转置,例如向量 A = [ A 1 , A 2 , A 3 , . . . , A N ] \boldsymbol{A=[A_1, A_2, A_3,...,A_N]} A=[A1,A2,A3,...,AN],则其转置为
A T = [ A 1 T A 2 T A 3 T . . . A N T ] (3-2-1) \boldsymbol{A}^T=\left[\begin{array}{l} \boldsymbol{A_1}^T\\ \boldsymbol{A_2}^T \\ \boldsymbol{A_3}^T \\ ...\\ \boldsymbol{A_N}^T \end{array}\right] \tag{3-2-1} AT= A1TA2TA3T...ANT (3-2-1)
(3) ( A B ) T = B T A T \boldsymbol{(AB)^T=B^TA^T} (AB)T=BTAT
(4)下面证明旋转矩阵 R \boldsymbol{R} R 是正交矩阵:
不妨设变换前后坐标系基底分别为 [ e 1 , e 2 , e 3 ] [\boldsymbol{e_1}, \boldsymbol{e_2}, \boldsymbol{e_3}] [e1,e2,e3] 和 [ e 1 ′ , e 2 ′ , e 3 ′ ] [\boldsymbol{e_1'}, \boldsymbol{e_2'}, \boldsymbol{e_3'}] [e1′,e2′,e3′],由于向量本身并未改变,则有
[ e 1 , e 2 , e 3 ] [ a 1 a 2 a 3 ] = [ e 1 ′ , e 2 ′ , e 3 ′ ] [ a 1 ′ a 2 ′ a 3 ′ ] (3-2-2) \left[\boldsymbol{e}_{1}, \boldsymbol{e}_{2}, \boldsymbol{e}_{3}\right]\left[\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=\left[\boldsymbol{e}_{1}^{\prime}, \boldsymbol{e}_{2}^{\prime}, \boldsymbol{e}_{3}^{\prime}\right]\left[\begin{array}{c} a_{1}^{\prime} \\ a_{2}^{\prime} \\ a_{3}^{\prime} \end{array}\right] \tag{3-2-2} [e1,e2,e3] a1a2a3 =[e1′,e2′,e3′] a1′a2′a3′ (3-2-2)
将上式两端分别左乘 [ e 1 T e 2 T e 3 T ] \left[\begin{array}{l} \boldsymbol{e_{1}^T} \\ \boldsymbol{e}_{2}^T \\ \boldsymbol{e}_{3}^T \end{array}\right] e1Te2Te3T 得到,
[ a 1 a 2 a 3 ] = [ e 1 T e 1 ′ e 1 T e 2 ′ e 1 T e 3 ′ e 2 T e 1 ′ e 2 T e 2 ′ e 2 T e 3 ′ e 3 T e 1 ′ e 3 T e 2 ′ e 3 T e 3 ′ ] [ a 1 ′ a 2 ′ a 3 ′ ] (3-2-3) \left[\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=\left[\begin{array}{lll} \boldsymbol{e}_{1}^T \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{1}^T \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{1}^T \boldsymbol{e}_{3}^{\prime} \\ \boldsymbol{e}_{2}^T \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{2}^T \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{2}^T \boldsymbol{e}_{3}^{\prime} \\ \boldsymbol{e}_{3}^T \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{3}^T \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{3}^T \boldsymbol{e}_{3}^{\prime} \end{array}\right]\left[\begin{array}{c} a_{1}^{\prime} \\ a_{2}^{\prime} \\ a_{3}^{\prime} \end{array}\right] \tag{3-2-3} a1a2a3 = e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′ a1′a2′a3′ (3-2-3)
则
R = [ e 1 T e 1 ′ e 1 T e 2 ′ e 1 T e 3 ′ e 2 T e 1 ′ e 2 T e 2 ′ e 2 T e 3 ′ e 3 T e 1 ′ e 3 T e 2 ′ e 3 T e 3 ′ ] (3-2-4) \boldsymbol{R}=\left[\begin{array}{lll} \boldsymbol{e}_{1}^T \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{1}^T \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{1}^T \boldsymbol{e}_{3}^{\prime} \\ \boldsymbol{e}_{2}^T \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{2}^T \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{2}^T \boldsymbol{e}_{3}^{\prime} \\ \boldsymbol{e}_{3}^T \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{3}^T \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{3}^T \boldsymbol{e}_{3}^{\prime} \end{array}\right] \tag{3-2-4} R= e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′ (3-2-4)
这是向量 a ′ \boldsymbol{a'} a′ 经旋转得到 a \boldsymbol{a} a 的旋转矩阵。
再将式 (3-8) 两端分别左乘 [ e 1 ′ T e 2 ′ T e 3 ′ T ] \left[\begin{array}{l} \boldsymbol{e_{1}'^T} \\ \boldsymbol{e}_{2}'^T \\ \boldsymbol{e}_{3}'^T \end{array}\right] e1′Te2′Te3′T 得到,
[ e 1 ′ T e 1 e 1 ′ T e 2 e 1 ′ T e 3 e 2 ′ T e 1 e 2 ′ T e 2 e 2 ′ T e 3 e 3 ′ T e 1 e 3 ′ T e 2 e 3 ′ T e 3 ] [ a 1 a 2 a 3 ] = [ a 1 ′ a 2 ′ a 3 ′ ] (3-2-5) \left[\begin{array}{lll} \boldsymbol{e}_{1}'^T \boldsymbol{e}_{1} & \boldsymbol{e}_{1}'^T \boldsymbol{e}_{2} & \boldsymbol{e}_{1}'^T \boldsymbol{e}_{3}\\ \boldsymbol{e}_{2}'^T \boldsymbol{e}_{1} & \boldsymbol{e}_{2}'^T \boldsymbol{e}_{2}& \boldsymbol{e}_{2}'^T \boldsymbol{e}_{3} \\ \boldsymbol{e}_{3}'^T \boldsymbol{e}_{1} & \boldsymbol{e}_{3}'^T \boldsymbol{e}_{2} & \boldsymbol{e}_{3}'^T \boldsymbol{e}_{3} \end{array}\right]\left[\begin{array}{c} a_{1} \\ a_{2}\\ a_{3} \end{array}\right]= \left[\begin{array}{l} a_{1}' \\ a_{2}' \\ a_{3}' \end{array}\right] \tag{3-2-5} e1′Te1e2′Te1e3′Te1e1′Te2e2′Te2e3′Te2e1′Te3e2′Te3e3′Te3 a1a2a3 = a1′a2′a3′ (3-2-5)
显然,这是向量 a \boldsymbol{a} a 经过反方向旋转得到 a ′ \boldsymbol{a'} a′ 的过程,那么有
R − 1 = [ e 1 ′ T e 1 e 1 ′ T e 2 e 1 ′ T e 3 e 2 ′ T e 1 e 2 ′ T e 2 e 2 ′ T e 3 e 3 ′ T e 1 e 3 ′ T e 2 e 3 ′ T e 3 ] (3-2-6) \boldsymbol{R^{-1}}=\left[\begin{array}{lll} \boldsymbol{e}_{1}'^T \boldsymbol{e}_{1} & \boldsymbol{e}_{1}'^T \boldsymbol{e}_{2} & \boldsymbol{e}_{1}'^T \boldsymbol{e}_{3}\\ \boldsymbol{e}_{2}'^T \boldsymbol{e}_{1} & \boldsymbol{e}_{2}'^T \boldsymbol{e}_{2}& \boldsymbol{e}_{2}'^T \boldsymbol{e}_{3} \\ \boldsymbol{e}_{3}'^T \boldsymbol{e}_{1} & \boldsymbol{e}_{3}'^T \boldsymbol{e}_{2} & \boldsymbol{e}_{3}'^T \boldsymbol{e}_{3} \end{array}\right] \tag{3-2-6} R−1= e1′Te1e2′Te1e3′Te1e1′Te2e2′Te2e3′Te2e1′Te3e2′Te3e3′Te3 (3-2-6)
根据分块矩阵转置规则,易得
R T = R − 1 (3-2-7) \boldsymbol{R^T = R^{-1}} \tag{3-2-7} RT=R−1(3-2-7)
证毕。
CH3-3 变换矩阵的逆的推导
(1)初等行变换法求矩阵的逆:将矩阵 A \boldsymbol{A} A 写成增广矩阵的形式即 ( A ∣ I ) \boldsymbol{(A | I)} (A∣I) ,经初等行变换,变为 ( I ∣ A − 1 ) \boldsymbol{(I | A^{-1})} (I∣A−1),则求出矩阵 A \boldsymbol{A} A 的逆。
(2)已知三维空间变换矩阵为:
T = [ R 3 × 3 t 3 × 1 0 T 1 ] (3-3-1) \boldsymbol{T}=\left[\begin{array}{ll} \boldsymbol{R}_{3\times3} & \boldsymbol{t}_{3\times1} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right] \tag{3-3-1} T=[R3×30Tt3×11](3-3-1)
写成增广矩阵
[ R 3 × 3 t 3 × 1 E 3 × 3 0 0 T 1 0 1 ] (3-3-2) \left[\begin{array}{cc|cc} \boldsymbol{R}_{3\times3} & \boldsymbol{t}_{3\times1} & \boldsymbol{E}_{3\times3} & 0 \\ \mathbf{0}^{\mathrm{T}} & 1 & 0 & 1\\ \end{array}\right] \tag{3-3-2} [R3×30Tt3×11E3×3001](3-3-2)
经过初等行变换,将前两列变为单位矩阵时,后两列即为 T − 1 \boldsymbol{T^{-1}} T−1。
首先,将第一行左乘 R 3 × 3 − 1 \boldsymbol{R}_{3\times3}^{-1} R3×3−1,上式变为
[ E 3 × 3 R 3 × 3 − 1 t 3 × 1 R 3 × 3 − 1 0 3 × 1 0 T 1 0 1 ] (3-3-3) \left[\begin{array}{cc|cc} \boldsymbol{E}_{3\times3} & \boldsymbol{R}_{3\times3}^{-1}\boldsymbol{t}_{3\times1} & \boldsymbol{R}_{3\times3}^{-1} & \boldsymbol{0}_{3\times1} \\ \mathbf{0}^{\mathrm{T}} & 1 & 0 & 1\\ \end{array}\right] \tag{3-3-3} [E3×30TR3×3−1t3×11R3×3−1003×11](3-3-3)
再将第二行乘 − R 3 × 3 − 1 t 3 × 1 -\boldsymbol{R}_{3\times3}^{-1}\boldsymbol{t}_{3\times1} −R3×3−1t3×1 ,加到第一行上,得
[ E 3 × 3 0 3 × 1 R 3 × 3 − 1 − R 3 × 3 − 1 t 3 × 1 0 T 1 0 1 ] (3-3-4) \left[\begin{array}{cc|cc} \boldsymbol{E}_{3\times3} & \boldsymbol{0}_{3\times1} & \boldsymbol{R}_{3\times3}^{-1} & -\boldsymbol{R}_{3\times3}^{-1}\boldsymbol{t}_{3\times1}\\ \mathbf{0}^{\mathrm{T}} & 1 & 0 & 1\\ \end{array}\right] \tag{3-3-4} [E3×30T03×11R3×3−10−R3×3−1t3×11](3-3-4)
又因为 R \boldsymbol{R} R 为正交矩阵,有 R − 1 = R T \boldsymbol{R^{-1}=R^T} R−1=RT。
则变换矩阵的逆矩阵为
T − 1 = [ R T − R T t 0 T 1 ] (3-3-5) \boldsymbol{T}^{-1}=\left[\begin{array}{cc} \boldsymbol{R}^{\mathrm{T}} & -\boldsymbol{R}^{\mathrm{T}} \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right] \tag{3-3-5} T−1=[RT0T−RTt1](3-3-5)
CH3-4 罗德里格斯公式推导
(1)注意绕轴旋转的方式,(类似直线绕轴旋转形成圆锥的过程),也就是说,该直线是母线,所绕的轴是中心线。
(2)向量点乘有交换律 a ⃗ ⋅ b ⃗ = b ⃗ ⋅ a ⃗ \vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a} a⋅b=b⋅a ;没有结合律,即 ( a ⃗ ⋅ b ⃗ ) ⋅ c ⃗ ≠ a ⃗ ⋅ ( b ⃗ ⋅ c ⃗ ) (\vec{a} \cdot \vec{b})\cdot\vec{c} \not=\vec{a} \cdot (\vec{b} \cdot \vec{c}) (a⋅b)⋅c=a⋅(b⋅c)。矩阵乘法有结合律即 ( A B ) C = A ( B C ) \boldsymbol{(AB)C=A(BC)} (AB)C=A(BC)。
(3)向量投影定理

如图,有
∣ a ⃗ ∣ c o s θ = a ⃗ ⋅ b ⃗ ∣ b ⃗ ∣ = a ⃗ ⋅ b 0 ⃗ (3-4-1) |\vec{a}|cos\theta=\frac {\vec{a}\cdot\vec{b}}{|\vec{b}|}=\vec{a}\cdot\vec{b_0} \tag{3-4-1} ∣a∣cosθ=∣b∣a⋅b=a⋅b0(3-4-1)
其中 b 0 ⃗ \vec{b_0} b0为与向量 b ⃗ \vec{b} b 同向的单位向量。
式(3-19)表示向量 a ⃗ \vec{a} a 在向量 b ⃗ \vec{b} b 上的投影的模长为 a ⃗ ⋅ b 0 ⃗ \vec{a}\cdot\vec{b_0} a⋅b0,那么,其在 b ⃗ \vec{b} b 上的投影向量为 ( a ⃗ ⋅ b 0 ⃗ ) ⋅ b 0 ⃗ (\vec{a}\cdot\vec{b_0})\cdot\vec{b_0} (a⋅b0)⋅b0。
(4)下面进行罗德里格斯公式的推导:

如上图所示,向量 v ⃗ \vec{v} v 绕 u ⃗ \vec{u} u 旋转 θ \theta θ 得到 v ′ ⃗ \vec{v'} v′,其中 u ⃗ \vec{u} u 是单位向量 。
① 向量 v ⃗ \vec{v} v分解: v ⃗ = v ⃗ ∥ + v ⃗ ⊥ \vec{v}=\vec{v}_{\parallel}+\vec{v}_{\perp} v=v∥+v⊥;
② 根据向量投影定理, v ⃗ ∥ = ( v ⃗ ⋅ u ⃗ ) ⋅ u ⃗ \vec{v}_{\parallel}=(\vec{v}\cdot\vec{u})\cdot\vec{u} v∥=(v⋅u)⋅u
③ 综合 ① ② ,得
v ⃗ ⊥ = v ⃗ − v ⃗ ∥ = v ⃗ − ( v ⃗ ⋅ u ⃗ ) ⋅ u ⃗ (3-4-2) \vec{v}_{\perp}=\vec{v}-\vec{v}_{\parallel}=\vec{v}-(\vec{v}\cdot\vec{u})\cdot\vec{u} \tag{3-4-2} v⊥=v−v∥=v−(v⋅u)⋅u(3-4-2)
④ 借助辅助向量 w ⃗ \vec{w} w,且 w ⃗ = u ⃗ × v ⃗ ⊥ \vec{w}=\vec{u}\times\vec{v}_{\perp} w=u×v⊥,即向量 w ⃗ \vec{w} w、 u ⃗ \vec{u} u、 v ⃗ ⊥ \vec{v}_{\perp} v⊥ 两两垂直。俯视图如下:

则有
w ⃗ = u ⃗ × v ⃗ ⊥ = u ⃗ × ( v ⃗ − v ⃗ ∥ ) = u ⃗ × v ⃗ − u ⃗ × v ⃗ ∥ = u ⃗ × v ⃗ (3-4-3) \begin{aligned} \vec{w}=\vec{u}\times\vec{v}_{\perp}=&\vec{u}\times(\vec{v}-\vec{v}_{\parallel})\\ =& \vec{u}\times\vec{v}-\vec{u}\times\vec{v}_{\parallel}\\ =& \vec{u}\times\vec{v} \end{aligned} \tag{3-4-3} w=u×v⊥===u×(v−v∥)u×v−u×v∥u×v(3-4-3)
⑤ 将 v ′ ⃗ ⊥ \vec{v'}_{\perp} v′⊥ 投影到 v ⃗ ⊥ \vec{v}_{\perp} v⊥ 和 $\vec{w} $ 上,则有
v ′ ⃗ ⊥ = v ⃗ v ′ + v ⃗ w ′ (3-4-4) \vec{v'}_{\perp}=\vec{v}_v'+\vec{v}_w' \tag{3-4-4} v′⊥=vv′+vw′(3-4-4)
⑥ 由上图
∣ v ′ ⃗ ⊥ ∣ = ∣ w ⃗ ∣ = ∣ v ⃗ ⊥ ∣ (3-4-5) |\vec{v'}_{\perp}|=|\vec{w}|=|\vec{v}_{\perp}| \tag{3-4-5} ∣v′⊥∣=∣w∣=∣v⊥∣(3-4-5)
且
∣ v ⃗ w ′ ∣ = ∣ v ′ ⃗ ⊥ ∣ s i n θ = ∣ w ⃗ ∣ s i n θ |\vec{v}_w'|=|\vec{v'}_{\perp}|sin\theta=|\vec{w}|sin\theta ∣vw′∣=∣v′⊥∣sinθ=∣w∣sinθ
结合式(2-23),有
v ⃗ w ′ = w ⃗ s i n θ (3-4-6) \vec{v}_w'=\vec{w}sin\theta \tag{3-4-6} vw′=wsinθ(3-4-6)
同理
∣ v ⃗ v ′ ∣ = ∣ v ⃗ ⊥ ∣ c o s θ |\vec{v}_v'|=|\vec{v}_{\perp}|cos\theta ∣vv′∣=∣v⊥∣cosθ
得
v ⃗ v ′ = v ⃗ ⊥ c o s θ (3-4-7) \vec{v}_v'=\vec{v}_{\perp}cos\theta \tag{3-4-7} vv′=v⊥cosθ(3-4-7)
⑦ 综合式(3-22)、(3-24)、(3-25),得
v ′ ⃗ ⊥ = v ⃗ v ′ + v ⃗ w ′ = v ⃗ ⊥ c o s θ + w ⃗ s i n θ (3-4-8) \vec{v'}_{\perp}=\vec{v}_v'+\vec{v}_w'=\vec{v}_{\perp}cos\theta+\vec{w}sin\theta \tag{3-4-8} v′⊥=vv′+vw′=v⊥cosθ+wsinθ(3-4-8)
⑧ 综上,
v ′ ⃗ = v ⃗ ∥ + v ′ ⃗ ⊥ = ( v ⃗ ⋅ u ⃗ ) ⋅ u ⃗ + v ⃗ ⊥ c o s θ + w ⃗ s i n θ = ( v ⃗ ⋅ u ⃗ ) ⋅ u ⃗ + ( v ⃗ − ( v ⃗ ⋅ u ⃗ ) ⋅ u ⃗ ) c o s θ + u ⃗ × v ⃗ s i n θ = ( v ⃗ ⋅ u ⃗ ) ⋅ u ⃗ + s i n θ u ⃗ × v ⃗ + c o s θ v ⃗ − c o s θ ( v ⃗ ⋅ u ⃗ ) ⋅ u ⃗ = c o s θ v ⃗ + ( 1 − c o s θ ) ( v ⃗ ⋅ u ⃗ ) ⋅ u ⃗ + s i n θ u ⃗ × v ⃗ (3-4-9) \begin{aligned} \vec{v'}=&\vec{v}_{\parallel}+\vec{v'}_{\perp}\\ =& (\vec{v}\cdot\vec{u})\cdot\vec{u}+\vec{v}_{\perp}cos\theta+\vec{w}sin\theta\\ =& (\vec{v}\cdot\vec{u})\cdot\vec{u}+(\vec{v}-(\vec{v}\cdot\vec{u})\cdot\vec{u})cos\theta+\vec{u}\times\vec{v}sin\theta\\ =& (\vec{v}\cdot\vec{u})\cdot\vec{u}+sin\theta\vec{u}\times\vec{v}+cos\theta\vec{v}-cos\theta(\vec{v}\cdot\vec{u})\cdot\vec{u}\\ =& cos\theta\vec{v}+(1-cos\theta)(\vec{v}\cdot\vec{u})\cdot\vec{u}+sin\theta\vec{u}\times\vec{v} \end{aligned} \tag{3-4-9} v′=====v∥+v′⊥(v⋅u)⋅u+v⊥cosθ+wsinθ(v⋅u)⋅u+(v−(v⋅u)⋅u)cosθ+u×vsinθ(v⋅u)⋅u+sinθu×v+cosθv−cosθ(v⋅u)⋅ucosθv+(1−cosθ)(v⋅u)⋅u+sinθu×v(3-4-9)
⑨ 设矩阵
u = [ u x u y u z ] , v = [ v x v y v z ] \boldsymbol{u}=\left[\begin{array}{c} u_{x} \\ u_{y}\\ u_{z} \end{array}\right], \boldsymbol{v}=\left[\begin{array}{c} v_{x} \\ v_{y}\\ v_{z} \end{array}\right] u= uxuyuz ,v= vxvyvz
1)将向量点乘转换为矩阵乘法,(此处应用向量交换律和矩阵结合律)
( v ⃗ ⋅ u ⃗ ) ⋅ u ⃗ = u ⃗ ⋅ ( v ⃗ ⋅ u ⃗ ) = u ( u T v ) = u u T v (3-4-10) (\vec{v}\cdot\vec{u})\cdot\vec{u}=\vec{u}\cdot(\vec{v}\cdot\vec{u})=\boldsymbol{u}(\boldsymbol{u}^T\boldsymbol{v})=\boldsymbol{u}\boldsymbol{u}^T\boldsymbol{v} \tag{3-4-10} (v⋅u)⋅u=u⋅(v⋅u)=u(uTv)=uuTv(3-4-10)
2)写成反对称矩阵形式
u ⃗ × v ⃗ = ∣ i j k u x u y u z v x v y v z ∣ = [ u y v z − u z v y u z v x − u x v z u x v y − u y v x ] = [ 0 − u z u y u z 0 − u x − u y u x 0 ] [ v x v y v z ] = u ∧ v (3-4-11) \vec{u}\times\vec{v}=\left| \begin{array}{cccc} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ u_{x} & u_{y} & u_{z}\\ v_{x} & v_{y} & v_{z} \end{array} \right|=\left[\begin{array}{c} u_{y}v_{z}-u_{z}v_{y} \\ u_{z}v_{x}-u_{x}v_{z}\\ u_{x}v_{y}-u_{y}v_{x} \end{array}\right]= \left[\begin{array}{c} 0 & -u_{z} & u_{y} \\ u_{z} & 0 & -u_{x}\\ -u_{y} & u_{x} & 0 \end{array}\right]\left[\begin{array}{c} v_{x}\\ v_{y}\\ v_{z} \end{array}\right]=\boldsymbol{u}^{\wedge}\boldsymbol{v} \tag{3-4-11} u×v= iuxvxjuyvykuzvz = uyvz−uzvyuzvx−uxvzuxvy−uyvx = 0uz−uy−uz0uxuy−ux0 vxvyvz =u∧v(3-4-11)
⑩ 因为 $ \boldsymbol{v’}=\boldsymbol{R}\boldsymbol{v}$
综上所述,式(3-27)可化为
R = c o s θ I + ( 1 − c o s θ ) u u T + s i n θ u ∧ (3-4-12) \boldsymbol{R}=cos\theta\boldsymbol{I}+(1-cos\theta)\boldsymbol{u}\boldsymbol{u}^T+sin\theta\boldsymbol{u}^{\wedge} \tag{3-4-12} R=cosθI+(1−cosθ)uuT+sinθu∧(3-4-12)
证毕。
(5)旋转矩阵到旋转向量的转换
将式(3-4-12)两边取迹,得
t r ( R ) = c o s θ t r ( I ) + ( 1 − c o s θ ) t r ( u u T ) + s i n θ t r ( u ∧ ) = 3 c o s θ + ( 1 − c o s θ ) + 0 = 1 + 2 c o s θ (3-4-13) \begin{aligned} tr(\boldsymbol{R})=& cos\theta tr(\boldsymbol{I})+(1-cos\theta)tr(\boldsymbol{u}\boldsymbol{u}^T)+sin\theta tr(\boldsymbol{u}^{\wedge})\\ =&3cos\theta+(1-cos\theta)+0\\ =&1+2cos\theta \end{aligned} \tag{3-4-13} tr(R)===cosθtr(I)+(1−cosθ)tr(uuT)+sinθtr(u∧)3cosθ+(1−cosθ)+01+2cosθ(3-4-13)
其中, t r ( u u T ) = u x 2 + u y 2 + u z 2 = 1 tr(\boldsymbol{u}\boldsymbol{u}^T)=u_x^2+u_y^2+u_z^2=1 tr(uuT)=ux2+uy2+uz2=1(向量 u \boldsymbol{u} u是单位向量,模长为1)。
那么,对于转角 θ \theta θ 有
θ = a r c c o s ( t r ( R ) − 1 2 ) (3-4-14) \theta=arccos(\frac {tr(\boldsymbol{R})-1} {2}) \tag{3-4-14} θ=arccos(2tr(R)−1)(3-4-14)
对于转轴 u \boldsymbol{u} u 有,
R u = u (3-4-15) \boldsymbol{Ru=u} \tag{3-4-15} Ru=u(3-4-15)
即转轴 u \boldsymbol{u} u 是旋转矩阵 R \boldsymbol{R} R 特征值为 1 对应的特征向量。
相关文章:

《视觉SLAM十四讲》公式推导(一)
文章目录 CH3 三维空间刚体运动CH3-1 旋转矩阵的推导CH3-2 旋转矩阵是正交矩阵的证明CH3-3 变换矩阵的逆的推导CH3-4 罗德里格斯公式推导 CH3 三维空间刚体运动 CH3-1 旋转矩阵的推导 (1)二维空间中的旋转矩阵 易得 { x ′ ∣ O P ′ ∣ c o s ( θ …...
简单好用的解压缩软件:keka 中文 for mac
Keka是一款功能全面、易于使用的文件压缩和解压缩软件,为Mac用户提供了便捷的文件管理工具。它支持多种压缩格式,具有快速解压和强大的压缩功能,让您能够轻松地处理各种文件压缩需求。 隐私非常重要 安全共享只需设置密码并创建高度加密的文…...

【UE 插件】UE4 虚幻引擎 插件开发(带源码插件打包、无源码插件打包) 有这一篇文章就够了!!!
目录 0 引言1 快速入门1.1 新建插件的前提1.2 创建插件步骤1.3 打包插件 2 无源代码的插件制作3 插件详细介绍3.1 插件的使用方法3.1 UE 预置插件模版3.1.1 空白3.1.2 纯内容3.1.3 编辑器独立窗口3.1.4 编辑器工具栏按钮3.1.5 编辑器模式3.1.6 第三方库3.1.7 蓝图库 3.2 插件中…...
C# CodeFormer 图像修复
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.Drawing; using System.Drawing.Imaging; using System.Windows.Forms;namespace 图像修复 {p…...

Android Studio的笔记--HttpURLConnection使用GET下载zip文件
HttpURLConnection使用GET下载zip文件 http get下载zip文件MainActivity.javaAndroidMainfest.xmlactivity_main.xmllog http get下载zip文件 MainActivity.java 用HttpURLConnection GET方法进行需注意: 1、Android 9及以上版本需要设置这个,否则会有…...
phantom3D模体
phantom是人头模型,分为2D和3D两种,matlab中可直接调用phantom(size)生成2D数据,如图1,而三维需要对应函数文件,下载:3D 图1 2D phantom 3D模体为一个椭球体,只能生成xyz三个方向相同维度的模…...

贪心算法解决批量开票限额的问题
具体问题:批量订单开票 限制:1.开最少的张数 2.每张限额10w # 贪心算法 def split_invoice_by_item(items):items_sorted sorted(items, keylambda x: x.price, reverseTrue)invoices []for item in items_sorted:# 尝试将商品加入已有的发票中added …...

Unity后台登录/获取数据——BestHTTP的使用Get/Post
一、使用BestHTTP实现登录功能(Post) 登录具体的步骤如下: 1:传入你的用户名和密码,这是一条包括链接和用户名密码的链接 2:使用BestHTTP的Post功能将链接传到服务器后台 3:后台拿到了你传送…...
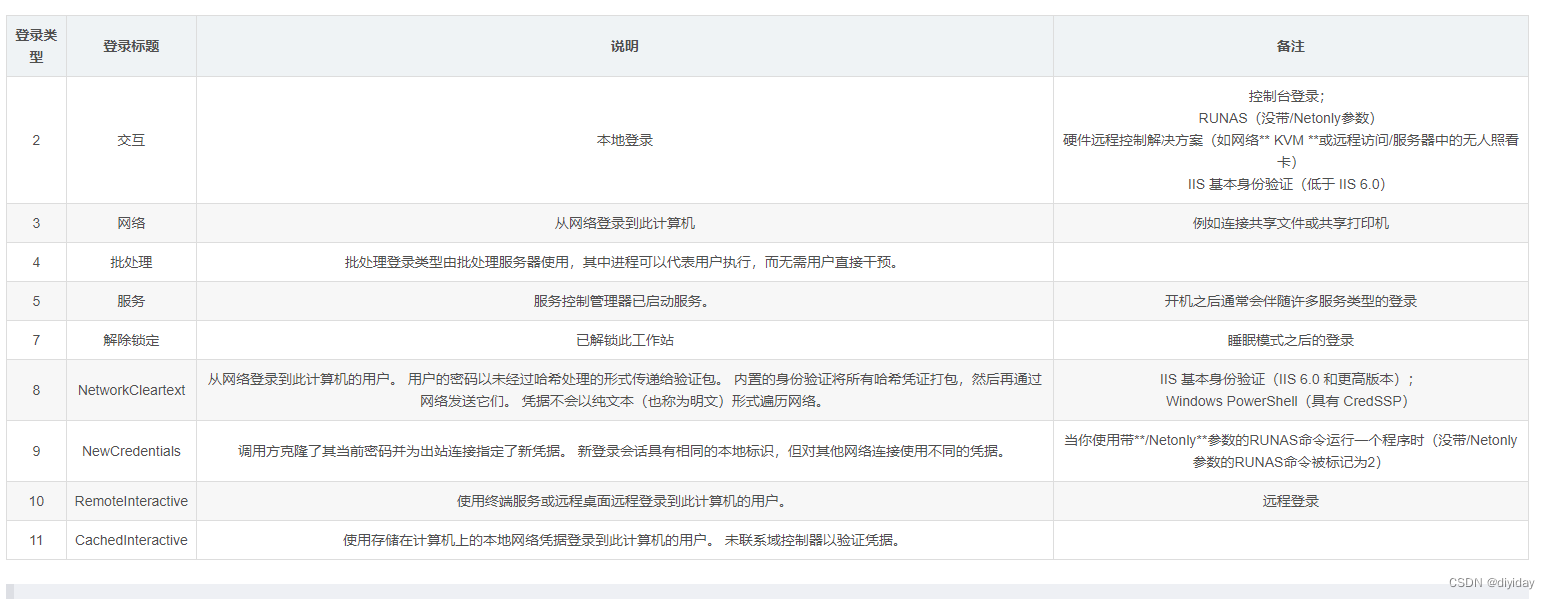
【Windows日志】记录系统事件的日志
文章目录 一、概要二、Windows日志介绍 2.1 应用程序日志2.2 系统日志2.3 安全日志 三、查看与分析日志四、常见事件ID 4.1 登录事件 4.1.1 4624登陆成功4.1.2 4625登陆失败 4.2 特权使用4.3 账户管理事件4.4 账户登录事件5.2 事件ID汇总 一、概要 Windows主要有以下三类日…...

物联网开发学习笔记——目录索引
什么是物联网? 物联网的英文名称是Internet of Things。IoT则是Internet of Things的缩写。 通俗地说,就是把设备与互联网连接起来,进行信息交互。 目录 一、开发环境配置 工欲善其事必先利其器,首先是开发环境配置。 开发环…...

Prometheus:优秀和强大的监控报警工具
文章目录 概述Prometheus的底层技术和原理数据模型数据采集数据存储查询语言数据可视化 Prometheus的部署Prometheus的使用配置数据采集目标查询监控数据设置警报规则 查看数据可视化总结 概述 Prometheus是一款开源的监控和警报工具,用于收集和存储系统和应用程序…...

Appium
# 获取元素和屏幕截图 echo on adb shell uiautomator dump /sdcard/app.uix adb pull /sdcard/app.uix F:\APP\app.uixadb shell screencap -p /sdcard/app.png adb pull /sdcard/app.png F:\APP\app.png卸载appium npm uninstall appium -g 重新安装appium npm install -g a…...
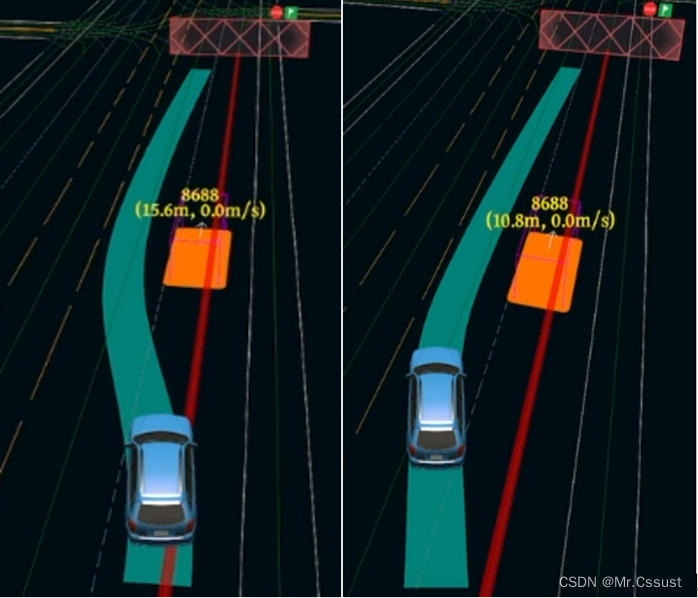
自动驾驶学习笔记(五)——绕行距离调试
#Apollo开发者# 学习课程的传送门如下,当您也准备学习自动驾驶时,可以和我一同前往: 《自动驾驶新人之旅》免费课程—> 传送门 《2023星火培训【感知专项营】》免费课程—>传送门 文章目录 前言 调试内容 打开在线编辑器 打开pl…...
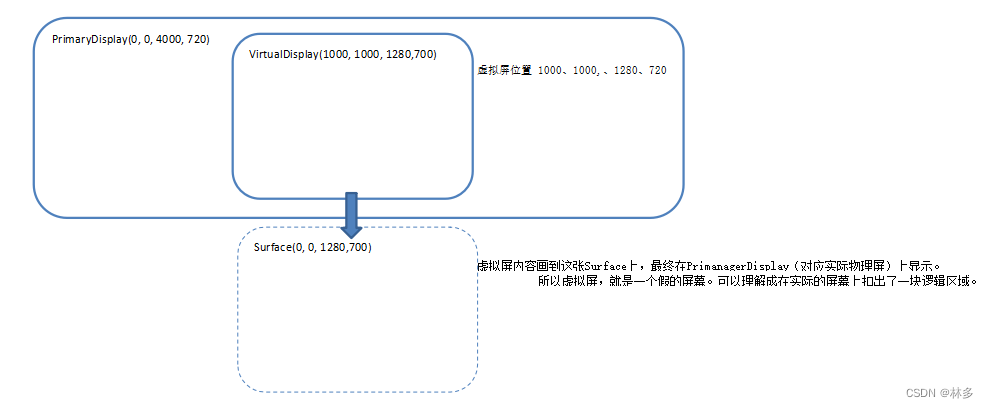
【Android】VirtualDisplay创建流程及原理
Android VirtualDisplay创建流程及原理 Android DisplayManager提供了createVirtualDisplay接口,用于创建虚拟屏。虚拟屏可用于录屏(网上很多资料说这个功能),分屏幕(比如一块很长的屏幕,通过虚拟屏分出不…...

Linux服务器快速搭建pytorch
Linux服务器搭建pytorch 文章目录 Linux服务器搭建pytorch一、使用FileZilla传输Anaconda二、激活Anaconda环境1.创建一个虚拟环境2.使用已有项目生成requirements.txt3.在虚拟环境中使用requirements.txt安装其他项目相关库 总结 一、使用FileZilla传输Anaconda 提示…...
声音克隆,定制自己的声音,使用最新版Bert-VITS2的云端训练+推理记录
说明 本次训练服务器使用Google Colab T4 GPUBert-VITS2库为:https://github.com/fishaudio/Bert-VITS2,其更新较为频繁,使用其2023.10.12的commit版本:主要参考:B站诸多大佬视频,CSDN:https://blog.csdn.…...

LeetCode讲解篇之198. 打家劫舍
LeetCode讲解篇之198. 打家劫舍 文章目录 LeetCode讲解篇之198. 打家劫舍题目描述题解思路题解代码 题目描述 题解思路 该问题可以通过递推来完成 递推公式: 前n间房的最大金额 max(前n-1间房的最大金额, 前n-2间房的最大金额第n-1间房的最…...
)
【下载共享文件】Java基于SMB协议 + JCIFS依赖下载Windows共享文件(亲测可用)
这篇文章,主要介绍如何使用JCIFS依赖库,基于SMB协议下载Windows共享文件。 目录 一、搭建Windows共享文件服务 1.1、创建共享文件目录 1.2、添加文件...

【评分卡实现】应用Python中的toad.ScoreCard函数实现评分卡
逻辑回归已经在各大银行和公司都实际运用于业务。之前的文章已经阐述了逻辑回归三部曲——逻辑回归和sigmod函数的由来、...
【数据结构】双链表的相关操作(声明结构体成员、初始化、判空、增、删、查)
双链表 双链表的特点声明双链表的结构体成员双链表的初始化带头结点的双链表初始化不带头结点的双链表初始化调用双链表的初始化 双链表的判空带头结点的双链表判空不带头结点的双链表判空 双链表的插入(按值插入)头插法建立双链表带头结点的头插法每次调…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
