当前位置： 首页 > news >正文

android 13.0 SystemUI导航栏添加虚拟按键功能(二)

news 2026/2/9 13:55:10

1.概述

    在13.0的系统产品开发中，对于在SystemUI的原生系统中默认只有三键导航，想添加其他虚拟按键就需要先在构建导航栏的相关布局
中分析结构，然后添加相关的图标xml就可以了，然后添加对应的点击事件，就可以了，接下来先分析第二步关于导航栏的相关布局情况
然后实现功能

2.SystemUI导航栏添加虚拟按键功能(二)的核心类

    frameworks/base/packages/SystemUI/src/com/android/systemui/statusbar/phone/NavigationBarInflaterView.javaframeworks/base/packages/SystemUI/res/values/config.xml

3.SystemUI导航栏添加虚拟按键功能(二)的核心功能分析和实现
   3.1在config.xml中增加虚拟按键volume音量虚拟按键的相关操作

   在第一节发现在config.xml中对于导航栏的布局信息就是在<string name="config_navBarLayout" translatable="false">left[.5W],back[1WC];home;recent[1WC],right[.5W]</string>
中定义的，然后在加载导航栏布局的时候，解析这些布局实现对布局的加载，所以在这里添加音量键的布局如下：
<string name="config_navBarLayout" translatable="false">left[.5W],back[1WC];home;recent[1WC],volume[1WC],right[.5W]</string>
从

相关文章：

android 13.0 SystemUI导航栏添加虚拟按键功能(二)

1.概述 在13.0的系统产品开发中，对于在SystemUI的原生系统中默认只有三键导航，想添加其他虚拟按键就需要先在构建导航栏的相关布局 中分析结构，然后添加相关的图标xml就可以了，然后添加对应的点击事件，就可以了，接下来先分析第二步关于导航栏的相关布局情况 然后实现功能…...

编程日记 2023/10/15 20:36:08

Java8 新特性之Stream（二）-- Stream的中间操作

目录 1.filter(Predicate) 2.map(Function) 3.flatMap(Function) 4.distinct() 5.sorted([Comparator]) 6.limit(n) 7.skip(n) 8.peek(Consumer)...

编程日记 2023/10/15 20:35:07

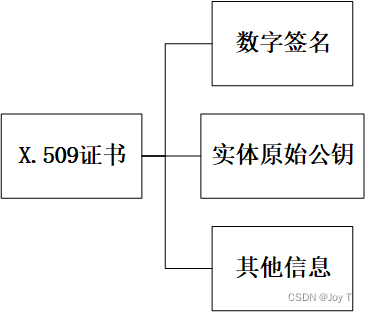
CA与区块链之数字签名详解

CA与区块链验证本质上都是数字签名&#xff0c;首先&#xff0c;我们看一下什么是数字签名&#xff01; 数字签名 数字签名是公钥密码学中的一种技术&#xff0c;用于验证信息的完整性和发送者的身份。简而言之&#xff0c;数字签名是一种确认信息来源和信息完整性的手段。它通…...

编程日记 2023/10/15 20:34:07

一文解读如何应用 REST 对资源进行访问？

文章目录 一、REST 简介二、涉及注解2.1 RequestMapping2.2 PathVariable2.3 RestController2.4 GetMapping、PostMapping、PutMapping、DeleteMapping补充&#xff1a;PathVariable、RequestBody、RequestParam 区别与应用 三、REST风格案例 一、REST 简介 REST (Representat…...

编程日记 2023/10/15 20:32:00

使用JAVA发送邮件

这里用java代码编写发送邮件我采用jar包&#xff0c;需要先点击这里下载三个jar包&#xff1a;这三个包分别为&#xff1a;additionnal.jar&#xff1b;activation.jar&#xff1b;mail.jar。这三个包缺一不可&#xff0c;如果少添加或未添加均会报下面这个错误&#xff1a; C…...

编程日记 2023/10/15 20:30:58

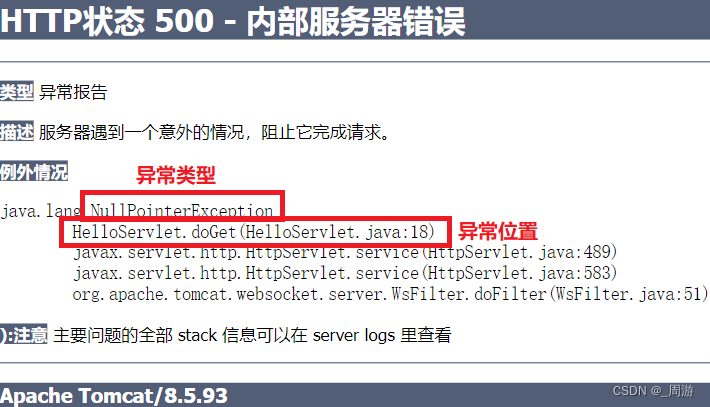
【JavaEE】_servlet程序的编写方法

目录 1. 创建项目 2. 引入依赖 3. 创建目录结构 3.1 在main目录下创建一个webapp目录 3.2 在webapp目录下创建一个WEB-INF目录 3.3 在WEB-INF目录下创建一个web.xml文件 3.4 在web.xml中进行代码编写 4. 编写代码 4.1 在java目录下创建类 4.2 打印"hello world&…...

编程日记 2023/10/15 20:29:57

美国市场三星手机超苹果 中国第一属华为

报告显示&#xff0c;截至5月份的三个月&#xff0c;iOS系统在美国、澳大利亚以及日本表现不俗。Android系统份额则在英国、德国以及法国实现增长。在中国城市地区&#xff0c;iOS份额同比基本持平&#xff0c;而Android份额则达到80.5%&#xff0c;同比增长1个百分点。 三星在…...

编程日记 2023/10/15 20:28:56

nodejs+vue+elementui医院挂号预约管理系统4n9w0

前端技术&#xff1a;nodejsvueelementui 前端&#xff1a;HTML5,CSS3、JavaScript、VUE 1、 node_modules文件夹(有npn install Express 框架于Node运行环境的Web框架, 开发语言 node.js 框架&#xff1a;Express 前端:Vue.js 数据库&#xff1a;mysql 数据库工具&#xff…...

编程日记 2023/10/15 20:27:55

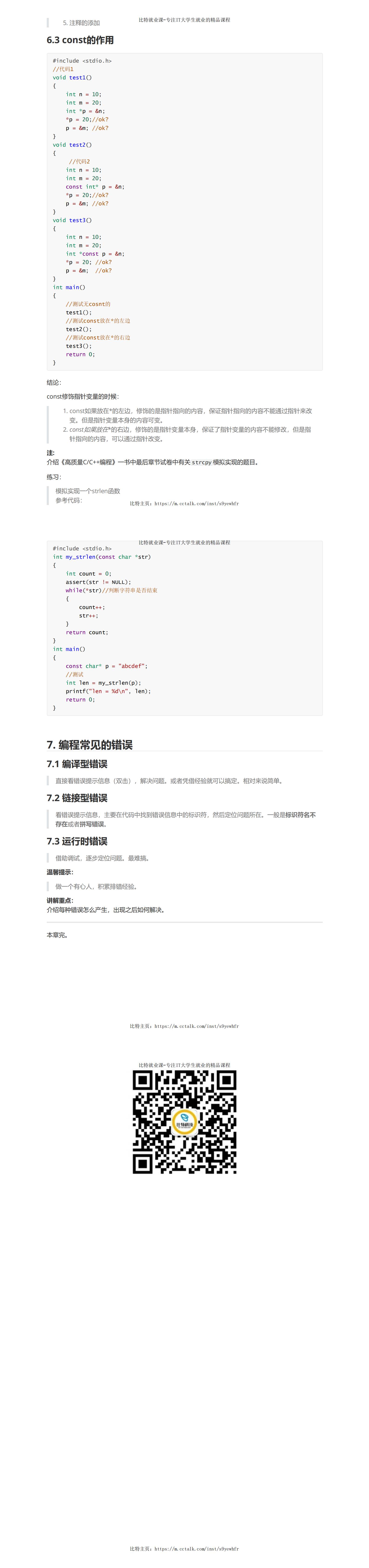
调试技巧（课件图解）

...

编程日记 2023/10/15 20:26:53

react中获取input输入框内容的两种方法

一.通过event对象信息的方式 <input onChange{(e)>this.inputChange(e)}/> <button onClick{()>this.getInputValue} >获取input的值</button>inputChange(e){alert(e.target.value)this.setState({username:e.target.value}) } getInputValue(){aler…...

编程日记 2023/10/15 20:25:50

Linux基础—1

1、命令行 1) 重要快捷键 按键作用Tab命令补全Ctrl强行终止当前程序Ctrld键盘输入结束或退出终端Ctrls暂停当前程序&#xff0c;暂停后按下任意键恢复运行Ctrlz将当前程序放到后台运行&#xff0c;恢复到前台为命令fgCtrla将光标移至输入行头&#xff0c;相当于Home键Ctrle将…...

编程日记 2023/10/15 20:24:47

十个面试排序算法

一、 前言 最常考的是快速排序和归并排序&#xff0c;并且经常有面试官要求现场写出这两种排序的代码。对这两种排序的代码一定要信手拈来才行。还有插入排序、冒泡排序、堆排序、基数排序、桶排序等。面试官对于这些排序可能会要求比较各自的优劣、各种算法的思想及其使用场景…...

编程日记 2023/10/15 20:22:43

技术学习群-第四期内容共享

本期是技术群聊的第四期。还是那句话&#xff0c;《群聊免费进入》。一起来看看本期分享内容。 uiautomator-Error问题 在使用u2的过程中&#xff0c;有时候需要使用到uiautomator这个工具来进行查阅层级。但是博主遇到了这么个问题。 《问题分析》&#xff1a;发生此问题的原因…...

编程日记 2023/10/15 20:21:40

冒泡排序/鸡尾酒排序

冒泡排序 冒泡排序&#xff08;Bubble Sort&#xff09;是一种简单的排序算法&#xff0c;它通过多次交换相邻元素的位置来实现排序。它的基本思想是从数组的第一个元素开始&#xff0c;比较相邻的两个元素&#xff0c;如果它们的顺序错误&#xff0c;则交换它们的位置。重复进…...

编程日记 2023/10/15 20:20:38

代码随想录算法训练营第五十三天|309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费

代码随想录算法训练营第五十三天|309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费 309.最佳买卖股票时机含冷冻期714.买卖股票的最佳时机含手续费 309.最佳买卖股票时机含冷冻期 题目链接&#xff1a;309.最佳买卖股票时机含冷冻期 文章链接 状态&#xff1a;有…...

编程日记 2023/10/15 20:19:34

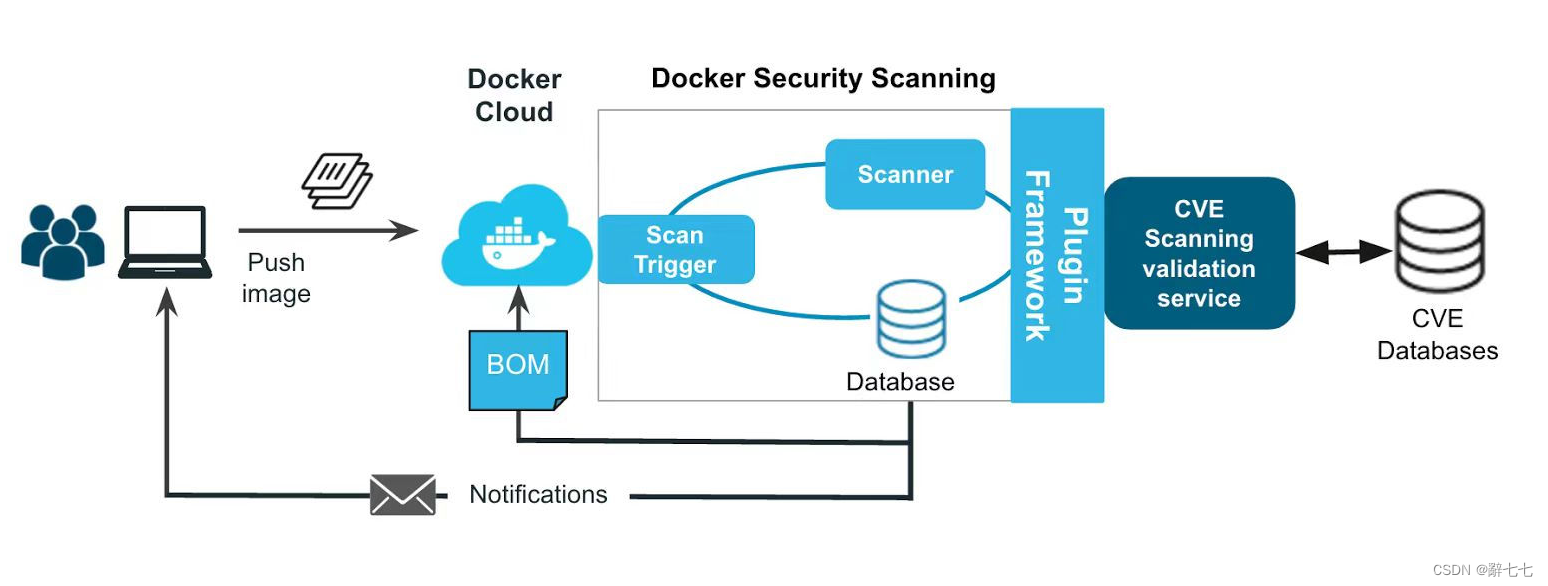
【Docker】Docker的使用案例以及未来发展、Docker Hub 服务、环境安全、容器部署安全

作者简介&#xff1a; 辭七七&#xff0c;目前大二&#xff0c;正在学习C/C&#xff0c;Java&#xff0c;Python等 作者主页&#xff1a; 七七的个人主页 文章收录专栏&#xff1a; 七七的闲谈 欢迎大家点赞 &#x1f44d; 收藏 ⭐ 加关注哦&#xff01;&#x1f496;&#x1f…...

编程日记 2023/10/15 20:17:32

qt qtabwidget获取当前选项卡的所有按键

要获取当前选项卡中的所有按键&#xff0c;可以通过以下步骤进行&#xff1a; 通过currentIndex()函数获取当前选项卡的索引。 使用widget()函数获取当前选项卡的QWidget。 连接QWidget的keyPressEvent事件&#xff0c;并在事件处理函数中获取按下的按键信息。 下面是示例代…...

编程日记 2023/10/15 20:16:30

为什么Excel插入图片不显示，点击能够显示

很久没有Excel了&#xff0c;今天在做Excel表格时&#xff0c;发现上传图片后不能显示&#xff0c;但是点击还是能够出现图片的 点击如下 点击能看到&#xff0c;但是不显示&#xff1f; 最后发现只需鼠标右键点击浮动即可显示...

编程日记 2023/10/15 20:15:28

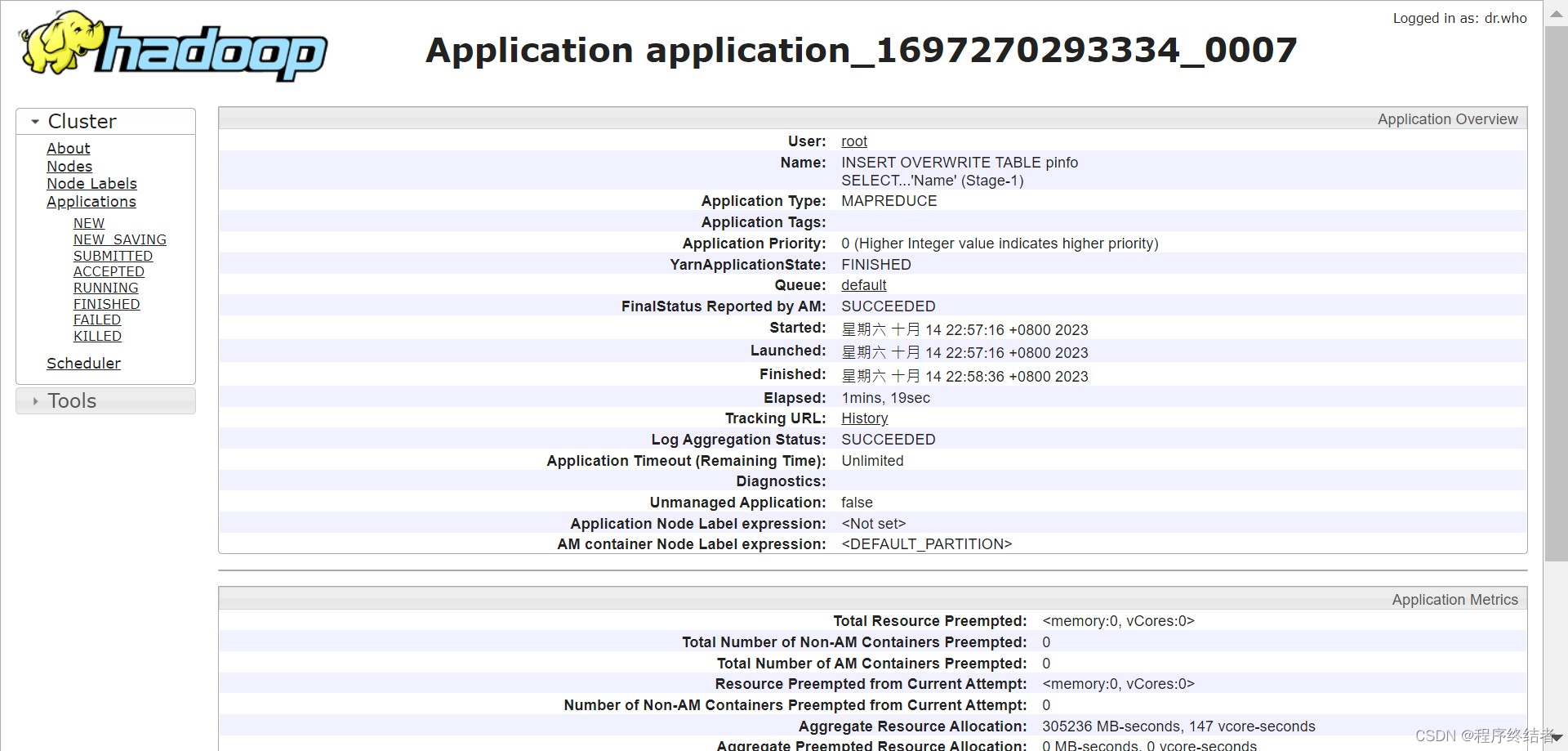
使用Python创建faker实例生成csv大数据测试文件并导入Hive数仓

文章目录 一、Python生成数据1.1 代码说明1.2 代码参考 二、数据迁移2.1 从本机上传至服务器2.2 检查源数据格式2.3 检查大小并上传至HDFS 三、beeline建表3.1 创建测试表并导入测试数据3.2 建表显示内容 四、csv文件首行列名的处理4.1 创建新的表4.2 将旧表过滤首行插入新表 一…...

编程日记 2023/10/15 20:14:25

qml基础语法

文章目录 基础语法例子 属性例子 核心元素元素item RectangleText例子 Image例子 MouseArea例子Component&#xff08;组件&#xff09;例子简单变换例子 定位器ColumnRowGridFlowRepeater 布局InputKeys 基础语法 QML是一种用于描述对象如何相互关联的声明式语言。  QtQuick是…...

编程日记 2023/10/15 20:13:25

FFmpeg 低延迟同屏方案

引言 在实时互动需求激增的当下&#xff0c;无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作&#xff0c;还是游戏直播的画面实时传输&#xff0c;低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架&#xff0c;凭借其灵活的编解码、数据…...

编程新知 2025/11/4 6:26:59

centos 7 部署awstats 网站访问检测

一、基础环境准备&#xff08;两种安装方式都要做&#xff09; bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats&#xff0…...

编程新知 2026/1/23 8:33:56

uniapp手机号一键登录保姆级教程（包含前端和后端）

目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号&#xff08;第三种&#xff09;后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

编程新知 2026/1/27 2:03:36

【Linux】Linux 系统默认的目录及作用说明

博主介绍&#xff1a;✌全网粉丝23W&#xff0c;CSDN博客专家、Java领域优质创作者&#xff0c;掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围&#xff1a;SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

编程新知 2026/1/29 2:30:31

深入理解Optional：处理空指针异常

1. 使用Optional处理可能为空的集合 在Java开发中&#xff0c;集合判空是一个常见但容易出错的场景。传统方式虽然可行&#xff0c;但存在一些潜在问题&#xff1a; // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

编程新知 2025/12/19 19:15:39

Python 高效图像帧提取与视频编码：实战指南

Python 高效图像帧提取与视频编码：实战指南 在音视频处理领域，图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库（如 OpenCV、FFmpeg、PyAV），可以高效处理视频流，实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程，提高处理…...

编程新知 2025/8/31 18:02:53

土建施工员考试：建筑施工技术重点知识有哪些？

《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目&#xff0c;核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容&#xff0c;附学习方向和应试技巧&#xff1a; 一、施工组织与进度管理 核心目标&#xff1a; 规…...

编程新知 2025/9/12 3:11:17

二叉树-144.二叉树的前序遍历-力扣(LeetCode)

一、题目解析 对于递归方法的前序遍历十分简单&#xff0c;但对于一位合格的程序猿而言&#xff0c;需要掌握将递归转化为非递归的能力&#xff0c;毕竟递归调用的时候会调用大量的栈帧&#xff0c;存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧&#xff0c;而非…...

编程新知 2026/2/5 3:46:26

标注工具核心架构分析——主窗口的图像显示

&#x1f3d7;️ 标注工具核心架构分析 &#x1f4cb; 系统概述 主要有两个核心类&#xff0c;采用经典的 Scene-View 架构模式&#xff1a; &#x1f3af; 核心类结构 1. AnnotationScene (QGraphicsScene子类) 主要负责标注场景的管理和交互 &#x1f527; 关键函数&…...

编程新知 2025/9/11 18:09:26

AWSLambda之设置时区

目标 希望Lambda运行的时区是东八区。 解决 只需要设置lambda的环境变量TZ为东八区时区即可&#xff0c;即Asia/Shanghai。 参考 使用 Lambda 环境变量...

编程新知 2026/1/28 11:08:49