【代码训练营】day41 | 01背包问题 416. 分割等和子集
所用代码 java
01背包理论
背包最大重量为:4
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
暴力:O(2^n)
动态规划:
1、二维dp数组 dp[i] [j]
-
dp数组含义:[0, i]物品,任取放进容量为j的背包里的最大价值
-
递推公式:
- 不放物品i :dp[i-1] [j]
- 放物品i:dp[i-1] [j - weight[i]] + value[i]
dp[i] [j] = Math.max(dp[i-1] [j], dp[i-1] [j - weight[i]] + value[i]
-
初始化:
dp[i] [j] i:物品 j:背包容量(0 1 2 3 4 )
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 物品0 | 0 | 15 | 15 | 15 | 15 |
| 物品1 | 0 | n => 由上和左上推出 | |||
| 物品2 | 0 |
- 遍历顺序:对于二维数组的01背包,先背包后物品,先物品后背包都可以
- 打印dp数组:
具体代码:
public class 背包01 {public static void main(String[] args) {int[] weight = {1,3,4};int[] value = {15,20,30};int bagSize = 4;bagProblem01(weight,value,bagSize);}public static void bagProblem01(int[] weight, int[] value, int bagSize){int goods = weight.length; // 物品数量int[][] dp = new int[goods][bagSize + 1];// 初始化 - 只有一个物品的时候,不管背包多大,加载都是该物品的价值for (int j = 0; j <= bagSize; j++) {dp[0][j] = value[0];}// 背包i在背包容量为0的时候,最大价值为0for (int i = 0; i < goods; i++) {dp[i][0] = 0;}// 先遍历背包,再遍历物品for (int i = 1; i < goods; i++) {for (int j = 1; j <= bagSize; j++) {if (j < weight[i]){// 当背包容量没有当我物品那么大时,就是放不下物品,最大的重量为i-1时最大重量dp[i][j] = dp[i-1][j];}else {// 可以放下物品时:比较放物品后的价值和没放物品价值谁大dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]);}}}// 打印dp数组for (int i = 0; i < goods; i++) {for (int j = 0; j <= bagSize; j++) {System.out.print(dp[i][j] + "\t");}System.out.println();}}
}
打印结果:
0 15 15 15 15
0 15 15 20 35
0 15 15 20 35
2、一维dp数组dp[j] - 滚动数组
- dp[j]:容量为j的背包最大价值为dp[j] i为物品
- 递推公式:dp[j] = max(dp[j], dp[j-weight[i]] + value[i])
- 初始化:dp[0] = 0 其他非负里面的最小值,如0。
- 遍历顺序:
- 先遍历物品,再遍历背包
- 倒序遍历,保证每个物品只被添加了一次。
- 打印dp数组
public static void bagProblem1(int[] weight, int[] value, int bagSize){int goods = weight.length; // 物品数量int[] dp = new int[bagSize + 1];// 初始化Arrays.fill(dp, 0);// 先遍历背包,再遍历物品for (int i = 0; i < goods; i++) {// j >= weight[i] 保证从右向左遍历的时候dp[j-weight[i]]不会越界for (int j = bagSize; j >= weight[i]; j--){dp[j] = Math.max(dp[j-1], dp[j-weight[i]] + value[i]);}}// 打印for (int MaxValue : dp) {System.out.print(MaxValue + "\t");}
}
分割等和子集 LeetCode 416
题目链接:分割等和子集 LeetCode 416 - 中等
思路
试了滑动窗口,不行。滑动窗口适合连续的数。
应该抽象为一个背包,背包的容量为数组和的一半,只要装下一半,另一半肯定可以。
- dp[j] :容量为j的背包能装下的最大价值为dp[j]
- 递推公式:dp[j] = max(dp[j], dp[j-nums[i]] + nums[i]) 重量和价值是相同的
- 初始化:dp[0] = 0;背包不可能是负数,需初始成非负整数的最大值 0
- 遍历方向:从右到左
- 打印dp数组
一维数组:
class Solution {public boolean canPartition(int[] nums) {int sum = 0;for (int num : nums) {sum += num;}if (sum % 2 == 1) return false;// target 相当于背包的容量int target = sum / 2;// dp数组初始为0int[] dp = new int[target + 1];// 物品for (int i = 0; i < nums.length; i++) {for (int j = target; j >= nums[i]; j--){dp[j] = Math.max(dp[j], dp[j-nums[i]] + nums[i]);}}// 看一下最后一个数是不是targetreturn dp[target] == target;}
}
二维数组:
- dp[i] [j] : 前i个数,其总价值不超过j的最大价值为dp[i] [j] j代表的是背包重量
- 递推公式:dp[i] [j] = Math.max(dp[i-1] [j], dp[i-1] [j - nums[i]] + nums[i]);
- 初始化:小于num[0]的不能装,初始化为0,其余为nums[0]
class Solution {public boolean canPartition(int[] nums) {int sum = 0;for (int num : nums) {sum += num;}if (sum % 2 == 1) return false;// target 相当于背包的容量int target = sum / 2;int[][] dp = new int[nums.length][target + 1];// 初始化,只有一个物品时的重量for (int j = 0; j <= target; j++) {dp[0][j] = j > nums[0] ? nums[0] : 0;}// 物品数量for (int i = 1; i < nums.length; i++) {// 背包容量,背包容量0,默认不能装for (int j = 1; j <= target; j++) {// 不能装下物品,最大值就是前一个值if (j < nums[i]){dp[i][j] = dp[i-1][j];}else {dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j - nums[i]] + nums[i]);}
// System.out.print("dp="+dp[i][j] + "\t");}
// System.out.println();}return dp[nums.length-1][target] == target;}
}
总结
本题主要是分析,只要把该题分析出来是背包问题的话,照着这个思路就非常的简单。
第二点就是二维数组在初始化的适合需要注意,背包重量小于nums[0]的数是没法装的,需初始化为0。
另外还有一种思路:
- dp[i] [j] : 从[0, i]区间中挑选一些正整数,每个数只能用一次,这些数的和恰好为 j
- 递推公式:dp[i] [j] = dp[i - 1] [j] || dp[i - 1] [j - nums[i]]
- 初始化:在num[0] < target 的情况下,第一个数只能让容积为自己的背包填满:dp[0] [num[0]] = true
class Solution {public boolean canPartition(int[] nums) {int sum = 0;for (int num : nums) sum+=num;if (sum % 2 == 1) return false;// target 相当于背包的容量int target = sum / 2;boolean[][] dp = new boolean[nums.length][target + 1];// 初始化,填满第一行的dp[0][nums[0]] 只有nums[0]本身if (nums[0] < target) dp[0][nums[0]] = true;// System.out.print("dp[0] = " + Arrays.toString(dp[0]));
// System.out.println();// 外层遍历物品数量for (int i = 1; i < nums.length; i++) {// 内层遍历背包for (int j = 0; j <= target; j++) {// 先取上一次的结果,后面进行修正dp[i][j] = dp[i-1][j];// 如果某个物品的重量恰好等于背包重量,则满足条件// 所以这一列的值都为trueif (nums[i] == j){dp[i][j] = true;
// System.out.print("***="+dp[i][j] + "\t\t");continue;}// 如果该物品小于背包的重量,就判断能否加入新的物品// dp[i-1][j]表示不放入背包,如果前面有满足条件,后面就一定可以满足// dp[i-1][j-nums[i]]表示放入背包,放入后判断放入背包的区间有没有满足条件的,就是左上if (nums[i] < j){dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]];}
// System.out.print("dp="+dp[i][j] + "\t\t");}
// System.out.println();}return dp[nums.length-1][target];}
}
相关文章:

【代码训练营】day41 | 01背包问题 416. 分割等和子集
所用代码 java 01背包理论 背包最大重量为:4 重量价值物品0115物品1320物品2430 暴力:O(2^n) 动态规划: 1、二维dp数组 dp[i] [j] dp数组含义:[0, i]物品,任取放进容量为j的背包里的最大价值 递推公式:…...

linux网络编程-多进程实现TCP并发服务器
服务端流程步骤socket函数创建监听套接字lfdbind函数将监听套接字绑定ip和端口listen函数设置服务器为被动监听状态,同时创建一条未完成连接队列(没走完tcp三次握手流程的连接),和一条已完成连接队列(已完成tcp三次握手…...
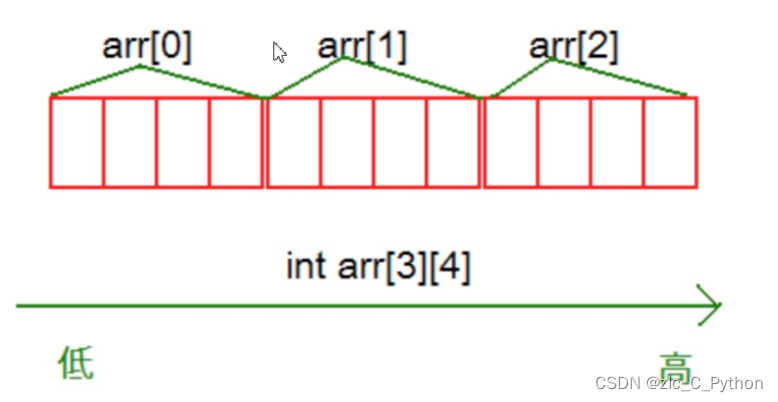
C语言的学习小结——数组
一、一维数组的创建与初始化 1、格式: type_t arr_name[const_n];//type_t 是指数组的元素类型 //const_n 是一个常量表达式,用来指定数组的大小 注: 数组是使用下标来访问的,下标从0开始。 数组的大小可以通过计算得到&…...
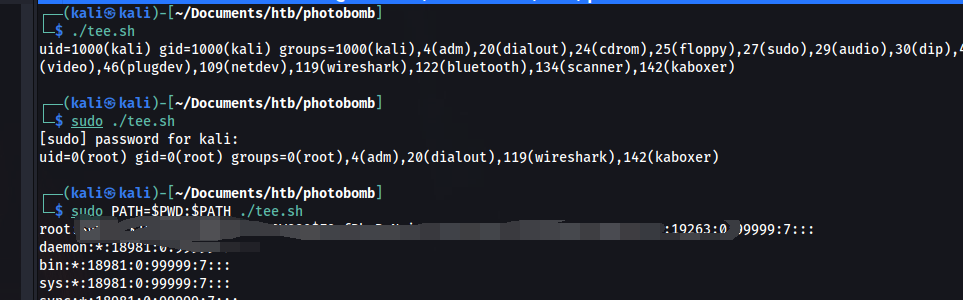
HTB-Photobomb
HTB-Photobomb信息收集开机提权对于问题的思考信息收集 端口扫描 目标首页 有一个http Authorization 目录扫描 在查看源码的时候发现了一个js文件。 并且发现了访问不存在的目录会出现错误提示。 通过搜索得知 Sinatra 是一个基于 Ruby 语言的 DSL(领域…...
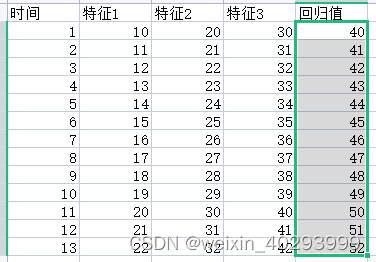
【LSTM】2 多因素单步骤预测
基于时间序列的预测,一定要明白它的原理,不是工作原理,而是工程落地原因。 基于时间序列,以已知回归未知----这两句话是分量很重的。 多因素单步单输出组合 时间序列:t1 是 特征 1,2,3 预测t2 的回归值41 多因素单步多…...

ChatGPT从下游应用“火”到了上游芯片厂,国内谁将受益?
因库存陷入低迷周期的半导体市场近日因ChatGPT的火热而重新受到外界关注。 原文链接:ChatGPT从下游应用“火”到了上游芯片厂,国内谁将受益? 由于ChatGPT属于生成式AI,被誉为“AI芯片”第一股的英伟达应声而涨。2月13日收盘&#…...

算法单调栈—Java版
单调栈 概念:维护栈中元素的单调性,单调增或者单调减。 什么时候用? 要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置。单调栈的本质是空间换时间,在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元…...

在Linux中进行rocketmq及rocketmq控制台安装与配置
rocketmq下载安装的版本:rocketmq-rocketmq-all-5.0.0.tar.gz rocketmq控制台下载安装的版本:rocketmq-externals-rocketmq-console-1.0.0.tar.gz rocketmq安装 第一步,下载server-jre-8u202-linux-x64.tar.gz安装包。 登录网址ÿ…...

2023年全国最新食品安全管理员精选真题及答案4
百分百题库提供食品安全管理员考试试题、食品安全员考试预测题、食品安全管理员考试真题、食品安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 31.国家对食品添加剂生产实行____制度。 A.产品注册 B.产品备案 C.登…...

es-07脚本查询
脚本查询 概念 Scripting是Elasticsearch支持的一种专门用于复杂场景下支持自定义编程的强大的脚本功能,ES支持多种脚本语言,如painless,其语法类似于Java,也有注释、关键字、类型、变量、函数等,其就要相对于其他脚本高出几倍的性…...

JM员工福利与健康平台,企业关怀Always Online
庄信万丰(Johnson Matthey, JM),全球性专用化学品公司,是可持续发展技术的全球领导者。在30多个国家和地区拥有13000多名员工。 JM的价值观之一是保护人类和地球。在生产过程中,JM保持对环境保护和能源清洁的高度关注;在员工福利…...
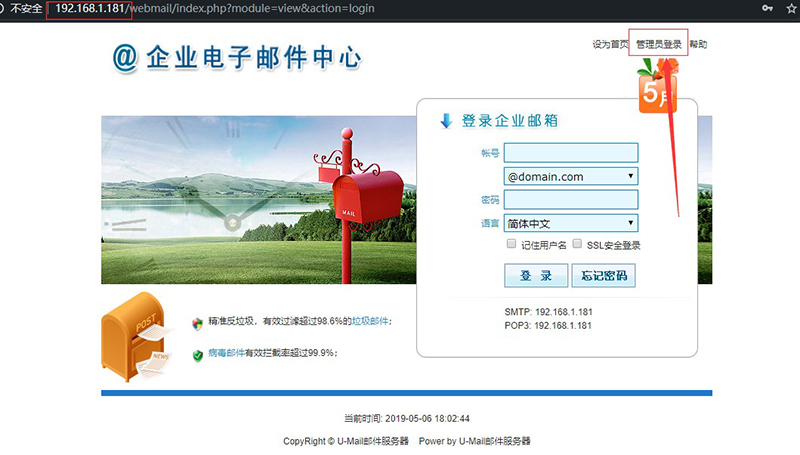
如何使用U-Mail搭建企业邮件服务器?
在当今的信息时代,企业也应该跟上时代的步伐。做好企业信息化建设,对企业事业单位尤为重要。电子邮件作为企业信息化过程中的重要组成部分,在企业内部沟通和外部沟通中发挥着重要作用。目前,有实力的企业已经开始倾向于自己搭建邮…...
用规则来搭建团队:写周报不一定是坏事
你好,我是Smile,一位有二十年工作经验的技术专家。今天我会结合我的经历,和你聊聊搭建技术团队这个话题。 众所周知,技术团队很大程度上决定了一个公司业务的生命力和生命周期,因此技术团队的投入成本往往很高&#x…...

Apollo使用方法
Apollo使用方法1.Apollo相关原理1.Apollo启动方法1.1 软件包方式1.2 脚本方式2.播放数据包2.1 软件包方式2.2 脚本方式3.试验planning模块4.从官网下载场景集其他工具1.Apollo相关原理 cyber / mainboard / mainboard.cc 是Apollo入口 cyber / mainboard / module_argument.cc…...

科研快讯 | 14篇论文被信号处理领域顶级国际会议ICASSP录用
ICASSP 2023 近日,2023年IEEE声学、语音与信号处理国际会议(2023 IEEE International Conference on Acoustics, Speech, and Signal Processing,ICASSP 2023)发布录用通知,清华大学人机语音交互实验室(TH…...
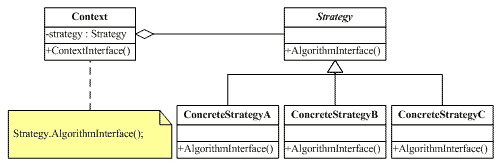
设计模式—策略(Strategy)模式
一、概述策略模式的用意是针对一组算法,将每一个算法封装到具有共同接口的独立的类中,从而使得它们可以相互替换。策略模式使得算法可以在不影响到客户端的情况下发生变化使用策略模式可以把行为和环境分割开来。环境类负责维持和查询行为类,…...

STM32 触摸屏移植GUI控制控件
目录 1、emWin 支持指针输入设备。 2、 模拟触摸屏驱动 3、实现触摸屏的流程 3.1 实现硬件函数 3.2 实现对GUI_TOUCH_Exec()的定期调用 3.3 使用上一步确定的值,在初始化函数LCD_X_Config()当中添加对GUI_TOUCH_Calibrate()的调用 4、…...
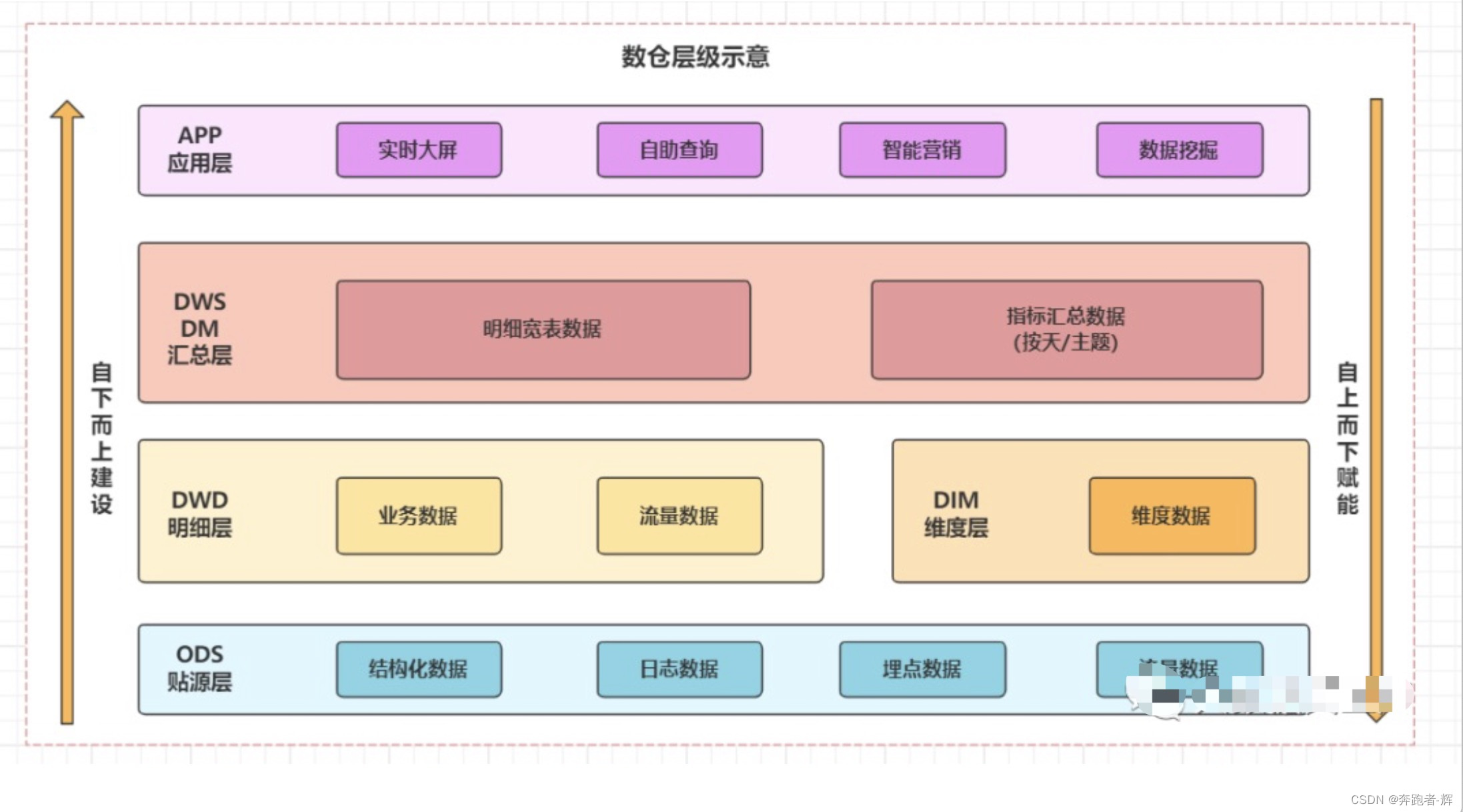
数仓模型之维度建模
目录 1、数仓架构原则 2、如何搭建一个好的数仓 2.1 建模方法 2.2 建模解决的痛点 2.3 数仓系统满足的特性 2.4 数仓架构设计 3、维度建模 4、案例 5、问题讨论 今天我们来聊聊在数仓模型中举足轻重的维度建模。 简单而言,数据仓库的核心目标是为展现层提…...
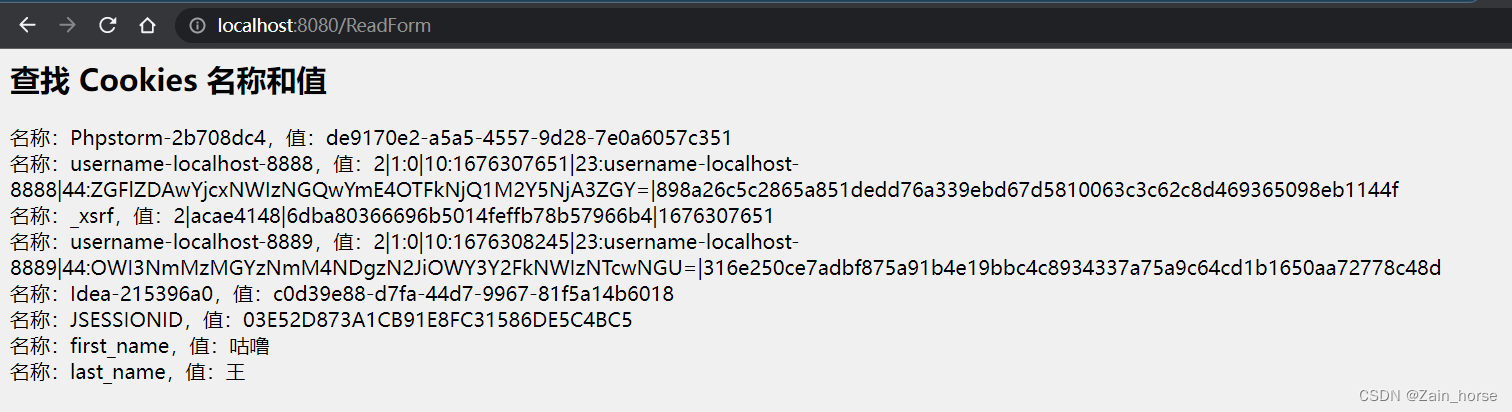
Servlet笔记(9):Cookie处理
一、Cookies处理 1、Cookies概念 Cookies是存储在客户端计算机上的文本文件,并保留各种跟踪信息。 识别返回用户的三个步骤 服务器脚本向浏览器发送一组Cookies。例如姓名、年龄或识别号码等。浏览器将这些信息存储在本地计算机上。当下一次浏览器向Web服务器发送…...

骨传导耳机是怎么传声的,选择骨传导耳机的时候需要注意什么?
骨传导耳机之所以能够成为当下最火的耳机,骨传导技术将声音转化为震动感,通过骨头进行传播,不会堵塞耳朵,就不会影响到周围环境音。这种技术也让骨传导耳机比传统入耳式耳机更安全,无需入耳式设计,避免了…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
