超详细树状数组讲解(+例题:动态求连续区间和)
树状数组的作用:
快速的对数列的一段范围求和
快速的修改数列的某一个数
为什么要使用树状数组:
大家从作用中看到快速求和的时候
可能会想到为什么不使用前缀和
只需要预处理一下就可以
在O(1)的时间复杂度下实行对于数列的一段范围的和
但是我们可以得到
当我们需要进行功能不仅含有
范围求和
还要求在同时对于
数列的某个数进行修改的时候
我们每次修改后还需要再求一次前缀和
这样的话时间复杂度最坏就达到了O(n)
所以我们就需要用到树状数组去实现这些功能
树状数组与线段树的区别:
他们之间的关系可以用包含关系来描述
也就是线段树包含了树状数组能够使用的功能
但树状数组的使用比线段树的使用快了很多倍
树状数组就像是一个专精的工具
效率高,但利用面相对于线段树不广。
树状数组的注意点以及图解:
注意点:
树状数组的下标为从1开始
对于树状数组的实现,我们通常采用一维数组来存储数列,其中奇数下标都为树状数组的第零层(也就是log2(lowbit(i))层),偶数下标为树状数组的log2(lowbit(i))层
提前创建两个数组:a[N]存原来给定的序列,tr[N]存构建的树状数组
构建的树状数组的详细图:

树状数组实现(3个核心函数):
函数一(lowbit()函数)
其中lowbit的作用是求二进制下最低位的1后面有多少个0
假如有k个0,那么就会返回2^k
具体实现:
int lowbit(int x){return x&(-x);
}//&是二进制的每个数位“与”的结果
//例如 0&1=0 0&0=0 1&1=1函数二(add()函数)
对于add函数他主要的作用就是
用来修改某一个位置上元素的值
当然我们在构建树状数组的时候
就可以用该函数去构建树状数组
具体实现:
void add(int x,int v){for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=y;
}函数三(query()函数)
对于query函数他主要的作用就是
用来询问前i个元素的和
我们一般用query(r)-query(l-1)来表示[l,r]区间的和
具体实现:
int query(int x){int sum=0;for(int i=x;i>=1;i-=lobit(i)) sum+=tr[i];return sum;
}题目:动态求连续区间和
题目详细:

代码详解:
#include<iostream>
using namespace std;const int N=1e5+6;int a[N],tr[N];
int n,m;int lowbit(int x){return x&(-x);
}void add(int x,int v){for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=v;
}int query(int x){int res=0;for(int i=x;i;i-=lowbit(i)) res+=tr[i]; return res;
}int main(){cin>>n>>m;for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) add(i,a[i]);while(m--){int k,x,y;scanf("%d%d%d",&k,&x,&y);if(1==k) add(x,y);else printf("%d\n",query(y)-query(x-1));}return 0;
}相关文章:

超详细树状数组讲解(+例题:动态求连续区间和)
树状数组的作用:快速的对数列的一段范围求和快速的修改数列的某一个数为什么要使用树状数组:大家从作用中看到快速求和的时候可能会想到为什么不使用前缀和只需要预处理一下就可以在O(1)的时间复杂度下实行对于数列的一段范围的和但是我们可以得到当我们…...

【学习笔记】AGC055
A - ABC Identity 如果只有AAA,BBB两种字符的话,我们发现要寻找p∈[1,n]p\in [1,n]p∈[1,n],使得[1:p][1:p][1:p]中AAA的数目与[p1:n][p1:n][p1:n]中BBB的数目相同。 如果有A,B,CA,B,CA,B,C三种字符,我们可以先将A,BA,BA,B分离出来…...
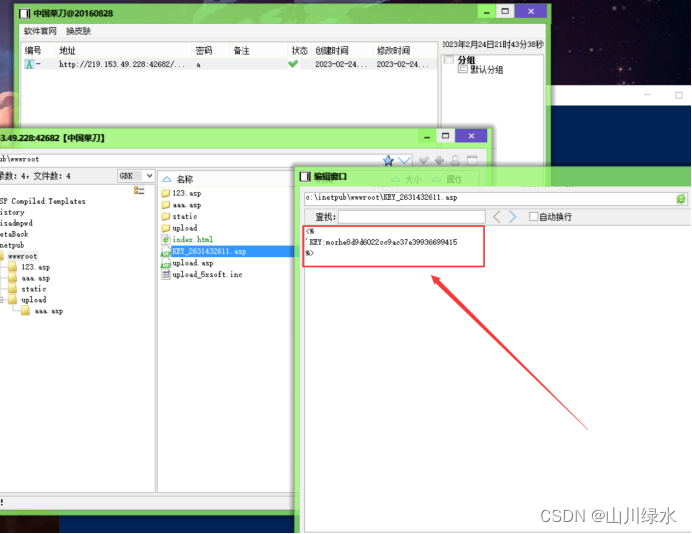
墨者——内部文件上传系统漏洞分析溯源 内部文件上传系统漏洞分析溯源
墨者——内部文件上传系统漏洞分析溯源 内部文件上传系统漏洞分析溯源 1.选择合适的文件上传 2.可以看到为*.asp文件 3.可以推测出此站点为IIS 4.上传shell.asp试试 5.上传报错,将其改名为shell.asp.txt上传,发现上传成功 6.有个问题就是服务器将我们所…...

5.2 Python if语句
5.2.3 检查是否不相等要判断两个值是否不等,可结合使用惊叹号和等号(!),其中的惊叹号表示不,在很多编程语言中都如此。下面再使用一条if语句来演示如何使用不等运算符。我们将把要求的比萨配料存储在一个变量中,再打印一条消息&am…...

ubuntu gerrit 配置
1 - 简介 参考地址: https://www.cnblogs.com/anliven/p/12019974.html https://www.cnblogs.com/anliven/p/11980432.html 虽然Gerrit 本身提供 Code Review和 Git 仓库的两大功能,但实际上很多项目用的是其他的Git仓库,例如GitLab和GitHub。 一般情况下,Gerrit位于最终…...

运动蓝牙耳机什么牌子好,运动蓝牙耳机品牌推荐
现在市面上运动耳机的品牌越来越多,还不知道选择哪一些运动耳机品牌,可以看看下面的一些耳机分享,运动耳机需要注意耳机的参数配置以及佩戴舒适度,根据自己最根本的使用需求来选择运动耳机。 1、南卡Runner Pro4骨传导蓝牙运动耳…...
C#传智:方法及参数、重载(第7天))
(7)C#传智:方法及参数、重载(第7天)
一、方法作用域 被调用者需要调用者的值,方法有二: 1.传参数. private static void Main(string[] args){int m 3;Console.WriteLine(m);Console.ReadKey();}public static int GetMax(int m){return m 3;} 2.使用静态字段模拟全局. 多个方法都需要时&#x…...

Python 函数式编程
函数式编程:允许把函数本身作为参数传入另一个函数,还允许返回一个函数! 1.高阶函数 一个函数可以接收另一个函数作为参数,这种函数称之为高阶函数 abs(-10) 是函数调用 abs是函数本身 abs函数名其实是一个变量名 变量可以…...
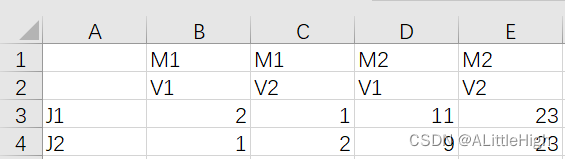
pandas读取EXCEL列名重复问题解决——pandas设置多行为列名(多层列名)
问题呈现 这是我在问答区看到的一个问题。 问:在python中使用pandas读取Excel数据,重复数据被区分了,如何做到重复数据不被区分? 解决思路 很明显,这是pandas读取excel文件时列名设置问题,我第一时间想…...

CMake常用语法
1. cmake_minimum_required(VERSION 3.4.1) 指定需要的最小的cmake版本 2. aux_source_directory 查找源文件并保存到相应的变量中: #查找当前目录下所有源文件并保存至SRC_LIST变量中 aux_source_directory(. SRC_LIST)3. add_library 3.1 添加一个库 add_library(<n…...
基础知识)
Java知识复习(一)基础知识
1、什么是JVM、JDK和JRE? JVM是指运行Java字节码的虚拟机。而字节码文件指的就是扩展名为.class的文件,JDK指功能齐全的Java SDK,能够创建和编译程序JRE指Java运行的环境,包括JVM、类库和命令等 2、重载和重写的主要区别 重载&…...
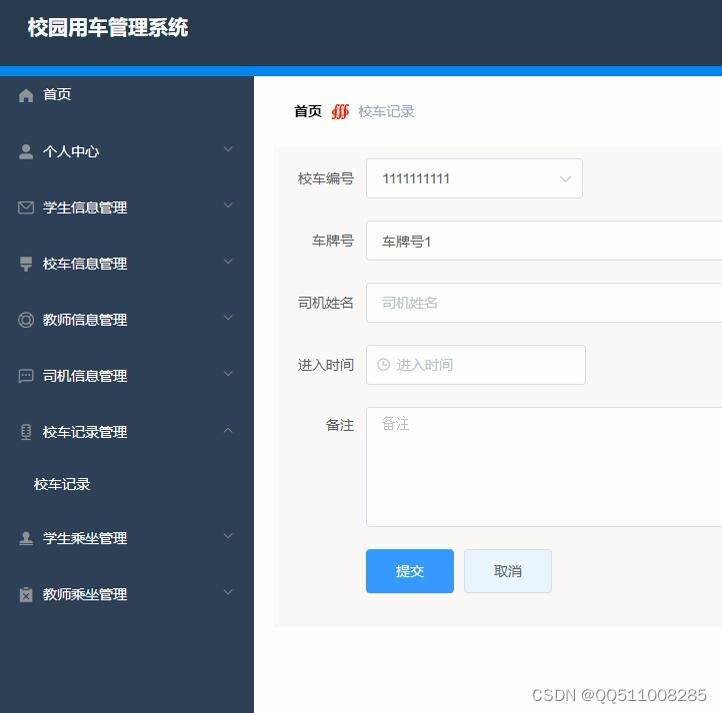
springboot+vue.js校园车辆用车预约管理系统
springboot是基于spring的快速开发框架, 相比于原生的spring而言, 它通过大量的java config来避免了大量的xml文件, 只需要简单的生成器便能生成一个可以运行的javaweb项目, 是目前最火热的java开发框架 前端技术:nodejsvueelementui本项目的应用场景描述如下&…...

【 K8s 源码之调度学习】Pod 间亲和性和反亲和性的源码分析
查看案例 字段含义podAffinityPod 间的亲和性定义podAntiAffinityPod 间的反亲和性定义requiredDuringSchedulingIgnoredDuringExecution硬性要求,必须满足条件,保证分散部署的效果最好使用用此方式preferredDuringSchedulingIgnoredDuringExecution软性…...

计及绿证交易及碳排放的含智能楼宇微网优化调度(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
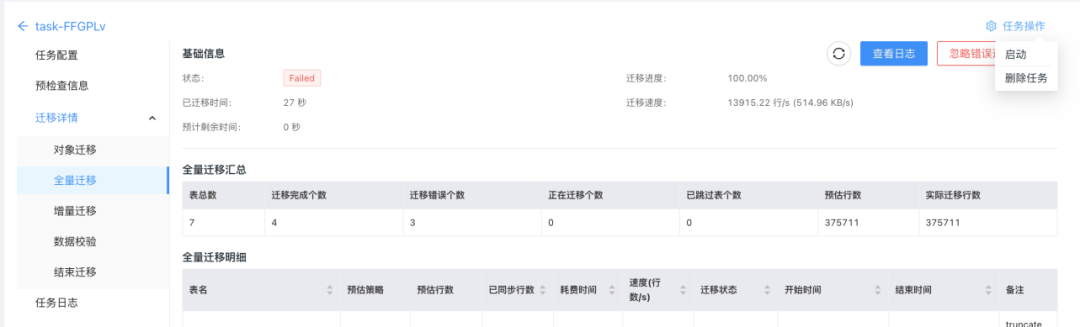
场景扩展,体验升级 | DBMotion新增无公网数据库迁移、支持监控报警等多项功能
丝滑的零停机数据库在线迁移工具——DBMotion,又双叒叕发新版:新增的网关、数据源功能,让你无公网IP的数据库也可以迁移;新增的监控功能,让你对迁移性能一目了然;新增的报警功能,让你及时获得同…...
【正点原子FPGA连载】第十五章eMMC读写测试实验 摘自【正点原子】DFZU2EG_4EV MPSoC之嵌入式Vitis开发指南
1)实验平台:正点原子MPSoC开发板 2)平台购买地址:https://detail.tmall.com/item.htm?id692450874670 3)全套实验源码手册视频下载地址: http://www.openedv.com/thread-340252-1-1.html 第十五章eMMC读写…...
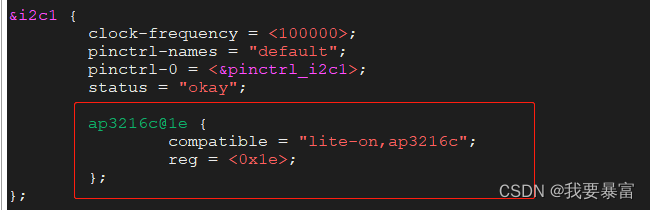
i2c子系统
i2c 硬件协议 Linux 应用层读写i2c 数据 在Linux系统上,不仅可以在内核中使用 i2c 总线发送、接收数据,同时也支持应用层使用i2c 总线发送、接收。 如果在内核中使能了drivers/i2c/i2c-dev.c 配置,内核就会为每一个i2c 控制器生成一个/dev/…...

【K3s】第17篇 Helm版本和支持的Kubernetes版本对照表
目录 Helm版本和支持的Kubernetes版本对照表 Helm版本和支持的Kubernetes版本对照表 描述了在Helm和Kubernetes之间支持的最大版本偏差。 Helm的版本用 x.y.z 描述,x是主版本,y是次版本,z是补丁版本。 当一个Helm的新版本发布时࿰…...
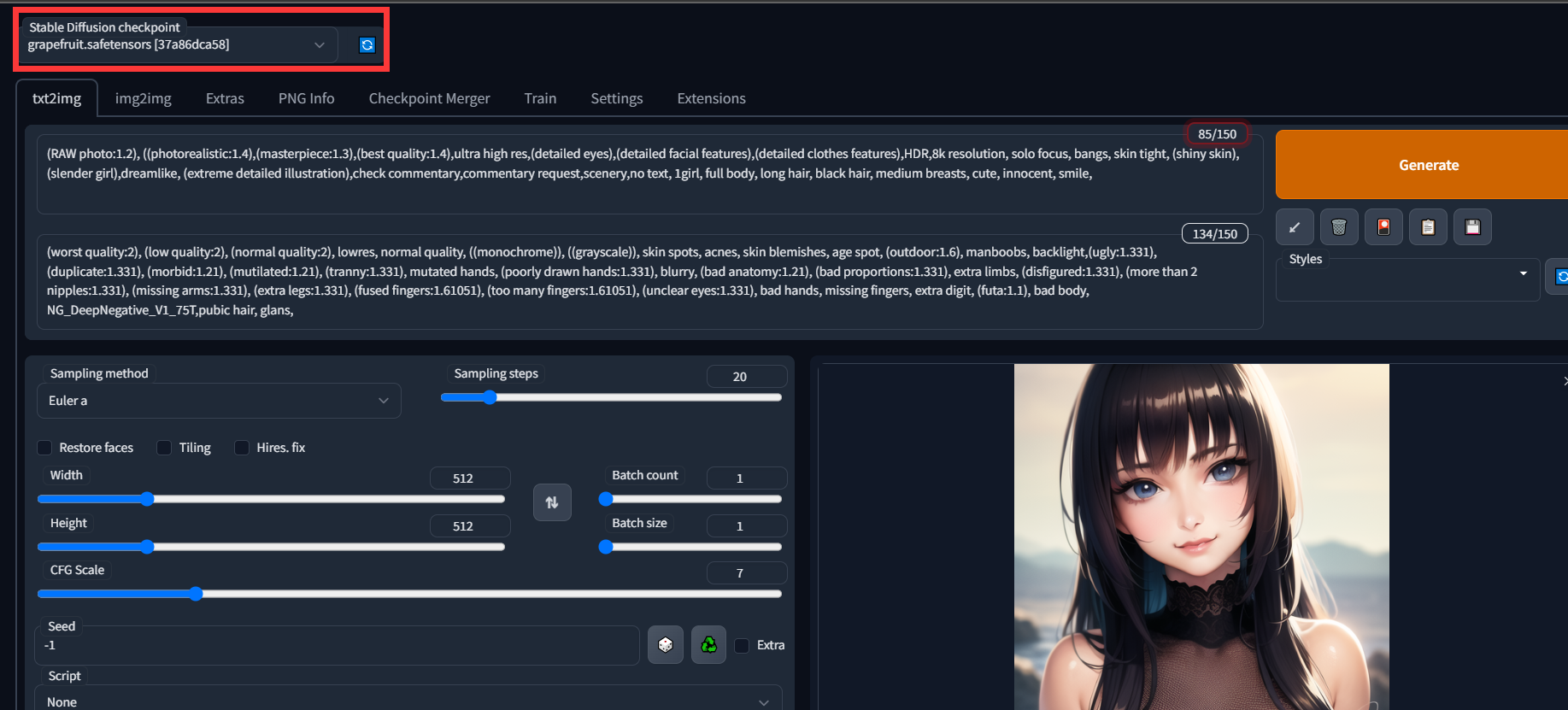
如何自己搭建一个ai画图系统? 从0开始云服务器部署novelai
如何自己搭建一个ai画图系统? 从0开始云服务器部署novelai 上面两张图都是通过ai生成的,是不是有以假乱真的感觉。 本教程提供的是自己搭建一个可以外网访问的ai系统的方法,需要采购gpu服务器(后续会出白嫖的方式)&…...

SpringSecurity过滤请求导致的系统bug
背景 今天开发一个新的会员管理系统,继承了SpringSecurity的,用以控制权限。结果无论怎么配置,都会报错:An Authentication object was not found in the SecurityContext 这句话的意思很明确:指的就是在SecurityCon…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
