2022最新版-李宏毅机器学习深度学习课程-P13 局部最小值与鞍点
一、优化失败的原因
局部最小值?鞍点?
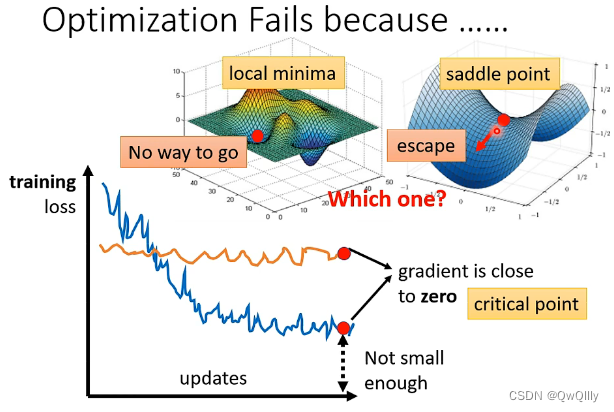
二、数学推导分析
用泰勒公式展开
一项与梯度(L的一阶导)有关,一项与海赛矩阵(L的二阶导)有关

海瑟矩阵
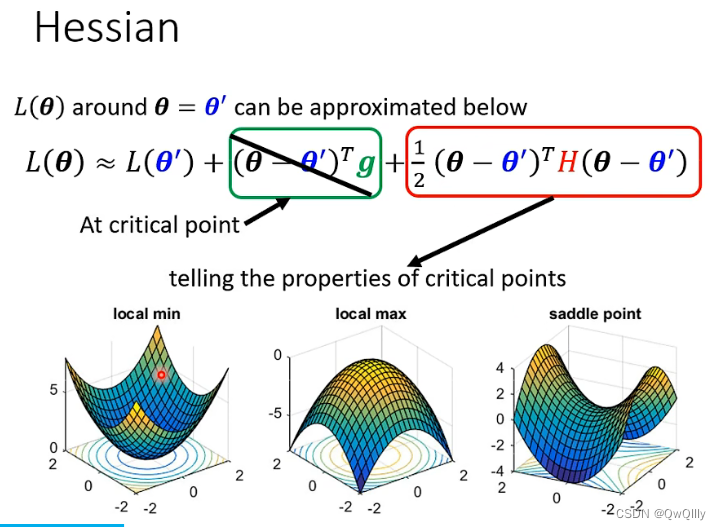
VTHV通过海瑟矩阵的性质可以转为判断H是否是正定的 来判断
- H正定=所有特征值为正=局部最小值
- H负定=所有特征值为负=局部最大值
- 有些特征值为正,有些为负=鞍点

例子
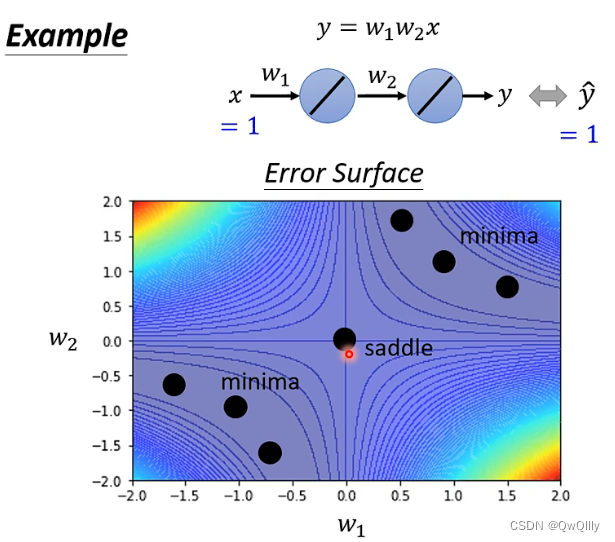
计算导数和海瑟矩阵的特征值
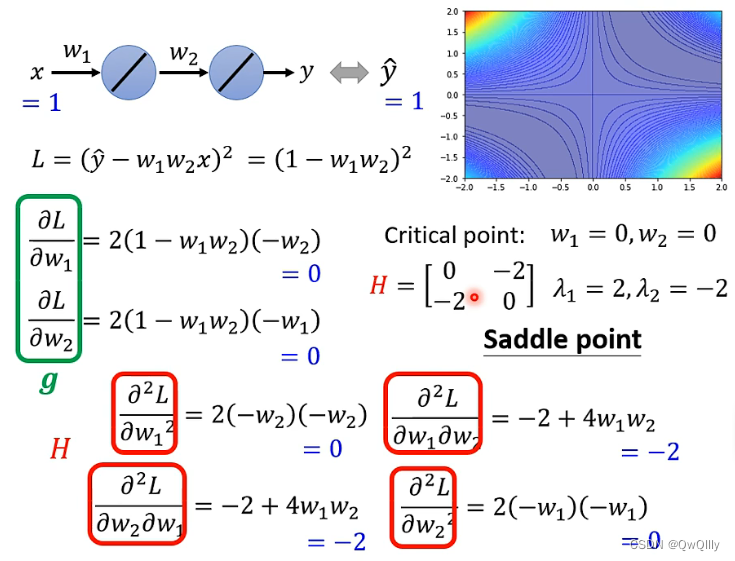
如果遇到鞍点,可以通过特征值来判断减小LOSS的方向:特征值为负的方向


其实局部最小值很少见,一升维,可能你碰上的就是个鞍点!
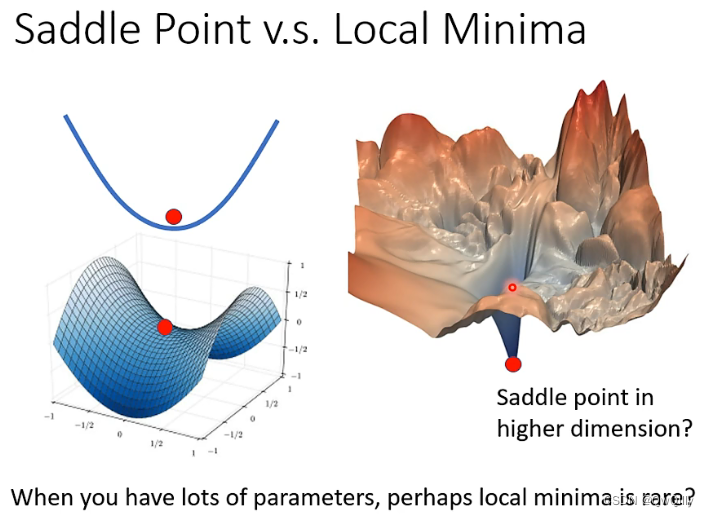
实验验证
注意这个方法肯定不是梯度下降法做的,做不出来,自己本身儿还一堆毛病呢。
纵轴:损失大小
横轴:局部最小值的比例=负特征值/全部特征值
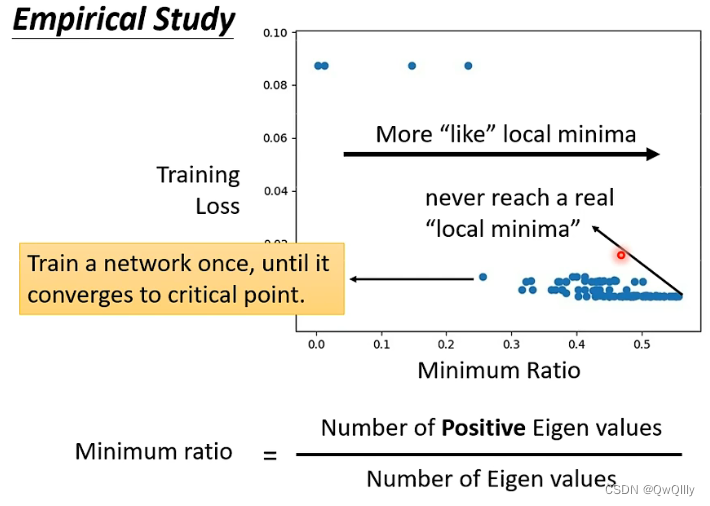
解决梯度太小被困住的问题。。。下一小节:动量!

相关文章:

2022最新版-李宏毅机器学习深度学习课程-P13 局部最小值与鞍点
一、优化失败的原因 局部最小值?鞍点? 二、数学推导分析 用泰勒公式展开 一项与梯度(L的一阶导)有关,一项与海赛矩阵(L的二阶导)有关 海瑟矩阵 VTHV通过海瑟矩阵的性质可以转为判断H是否是正…...
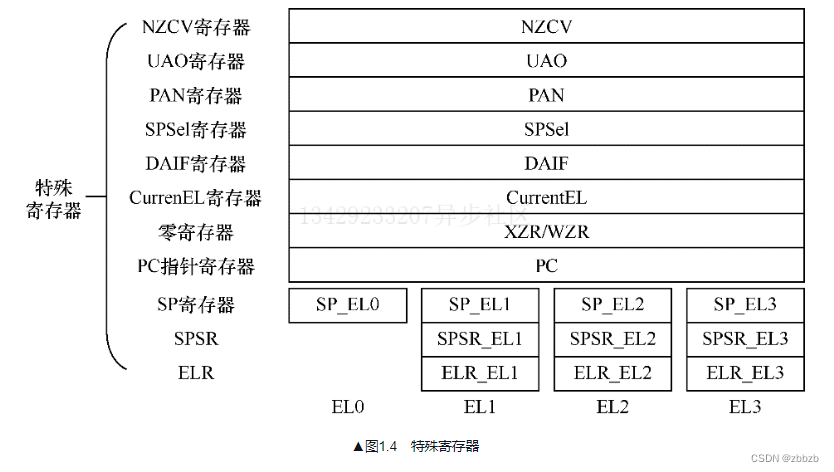
ARM架构的基本知识
ARM两种授权 体系结构授权, 一种硬件规范, 用来约定指令集, 芯片内部体系结构(内存管理, 高速缓存管理), 只约定每一条指令的格式, 行为规范, 参数, 客户根据这个规范自行设计与之兼容的处理器处理IP授权, ARM公司根据某个版本的体系结构设计处理器, 再把处理器设计方案授权给…...

网络安全(黑客技术)——如何高效自学
前言 前几天发布了一篇 网络安全(黑客)自学 没想到收到了许多人的私信想要学习网安黑客技术!却不知道从哪里开始学起!怎么学?如何学? 今天给大家分享一下,很多人上来就说想学习黑客,…...
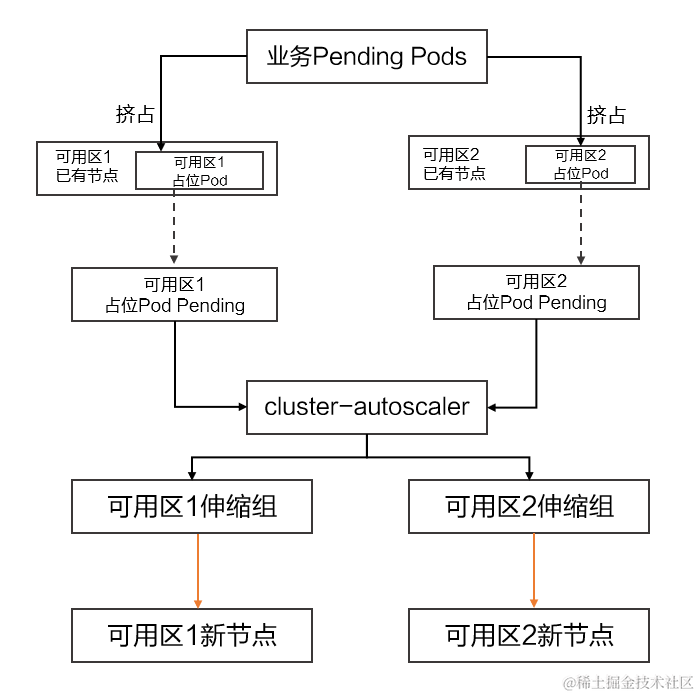
云原生场景下高可用架构的最佳实践
作者:刘佳旭(花名:佳旭),阿里云容器服务技术专家 引言 随着云原生技术的快速发展以及在企业 IT 领域的深入应用,云原生场景下的高可用架构,对于企业服务的可用性、稳定性、安全性越发重要。通…...

图论-最短路径算法-弗洛伊德算法与迪杰斯特拉算法
弗洛伊德算法: 弗洛伊德算法本质是动态规划,通过添加点进如可选择的点组成的集合的同时更新所有点之间的距离,从而得到每两个点之间的最短距离。 初始化: 创建一个二维数组 dist,其中 dist[i][j] 表示从节点 i 到节点…...

[23] IPDreamer: Appearance-Controllable 3D Object Generation with Image Prompts
pdf Text-to-3D任务中,对3D模型外观的控制不强,本文提出IPDreamer来解决该问题。在NeRF Training阶段,IPDreamer根据文本用ControlNet生成参考图,并将参考图作为Zero 1-to-3的控制条件,用基于Zero 1-to-3的SDS损失生成…...

深入理解React中的useEffect钩子函数
引言: React是一种流行的JavaScript库,它通过组件化和声明式编程的方式简化了前端开发。在React中,一个核心概念是组件的生命周期,其中包含了许多钩子函数,用于管理组件的不同阶段。其中之一就是useEffect钩子函数&…...

数字化时代的财务管理:挑战与机遇
导语:随着数字化技术的不断发展,财务管理正面临着前所未有的挑战和机遇。数字化不仅改变了财务数据的收集、处理和分析方式,还为财务决策提供了更多的依据和方向。本文将探讨数字化时代财务管理的新特点,以及如何利用数字化技术提…...
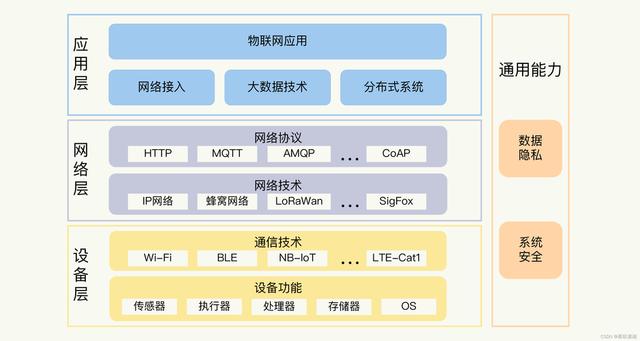
网络通信协议-HTTP、WebSocket、MQTT的比较与应用
在今天的数字化世界中,各种通信协议起着关键的作用,以确保信息的传递和交换。HTTP、WebSocket 和 MQTT 是三种常用的网络通信协议,它们各自适用于不同的应用场景。本文将比较这三种协议,并探讨它们的主要应用领域。 HTTPÿ…...
、dataloader、长短期记忆网络(LSTM)、门控循环单元(GRU)、超参数对比)
【深度学习】深度学习实验四——循环神经网络(RNN)、dataloader、长短期记忆网络(LSTM)、门控循环单元(GRU)、超参数对比
一、实验内容 实验内容包含要进行什么实验,实验的目的是什么,实验用到的算法及其原理的简单介绍。 1.1 循环神经网络 (1)理解序列数据处理方法,补全面向对象编程中的缺失代码,并使用torch自带数据工具将数据封装为dataloader。 (2)分别采用手动方式以及调用接口方式…...

DB2分区表详解
一、分区表基本概念 当表中的数据量不断增大,查询数据的速度就会变慢,应用程序的性能就会下降,这时就应该考虑对表进行分区。分区后的表称为分区表。 表进行分区后,逻辑上表仍然是一张完整的表,只是将表中的数据在物理上存放到多个“表空间”(物理文件上),这样查询数据时…...

基本地址变换机构
基本地址变换机构:用于实现逻辑地址到物理地址转换的一组硬件机构。 关于页号页表的定义,放个本人的传送门 1.页表寄存器 基本地址变换机构可以借助进程的页表将逻辑地址转换为物理地址。 1.作用 通常会在系统中设置一个页表寄存器(PTR&…...
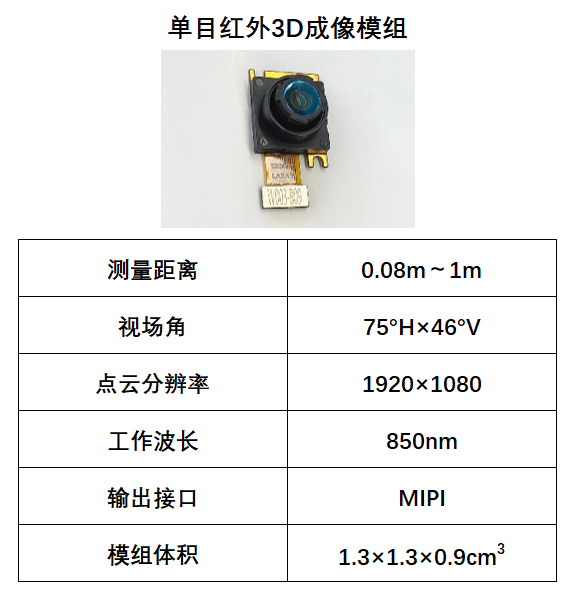
以单颗CMOS摄像头重构三维场景,维悟光子发布单目红外3D成像模组
维悟光子近期发布全新单目红外3D成像模组,现可提供下游用户进行测试导入。通过结合微纳光学元件编码和人工智能算法解码,维悟光子单目红外3D成像模组采用单颗摄像头,通过单帧拍摄,可同时获取像素级配准的3D点云和红外图像信息,可被应用于机器人、生物识别等广阔领域。 市场…...
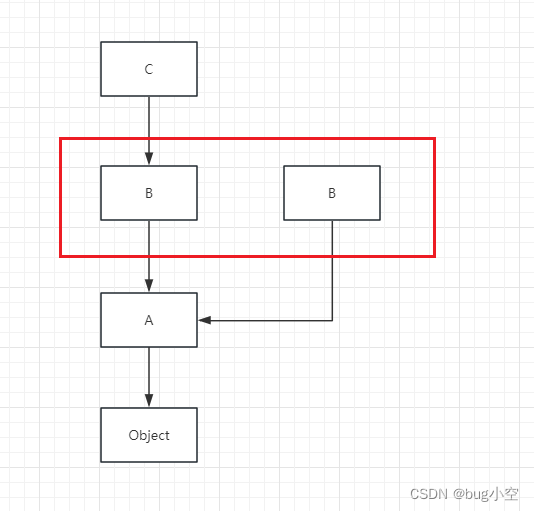
Jinja2模板注入 | python模板注入特殊属性 / 对象讲解
在进行模板利用的时候需要使用特殊的属性和对象进行利用,这里对这些特殊属性及方法进行讲解 以下实验输出python3版本为 3.10.4, python2版本为 2.7.13 特殊属性 __class__ 类实例上使用,它用于获取该实例对应的类__base__ 用于获取父类__mr…...

一致性公式证明
首先,假设存在两个不同的聚类假设 f 1 f^1 f1和 f 2 f^2 f2,它们在两个视角上的聚类结果分别为 y 1 ∈ { − 1 , 1 } n y^1\in\{-1,1\}^n y1∈{−1,1}n和 y 2 ∈ { − 1 , 1 } n y^2\in\{-1,1\}^n y2∈{−1,1}n。 证明一致性不等式: …...
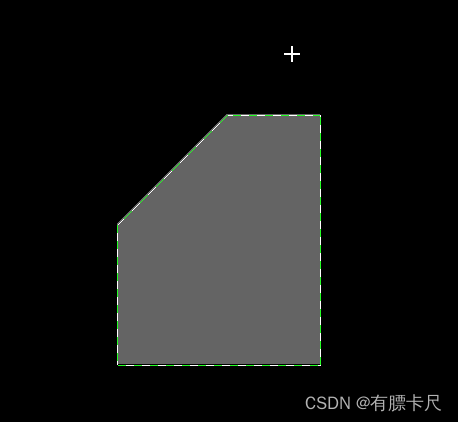
allegro中shape的一些基本操作(一)——添加和修改shape
添加shape 简单添加shape的方式有3种,如下图所示 点击选择相应的shape模式后可以在option面板中设置相应的shape参数(这里不做过多介绍,里面可以设置shape的大小、静态或动态shape等参数),然后再用鼠标在相应的层上添…...
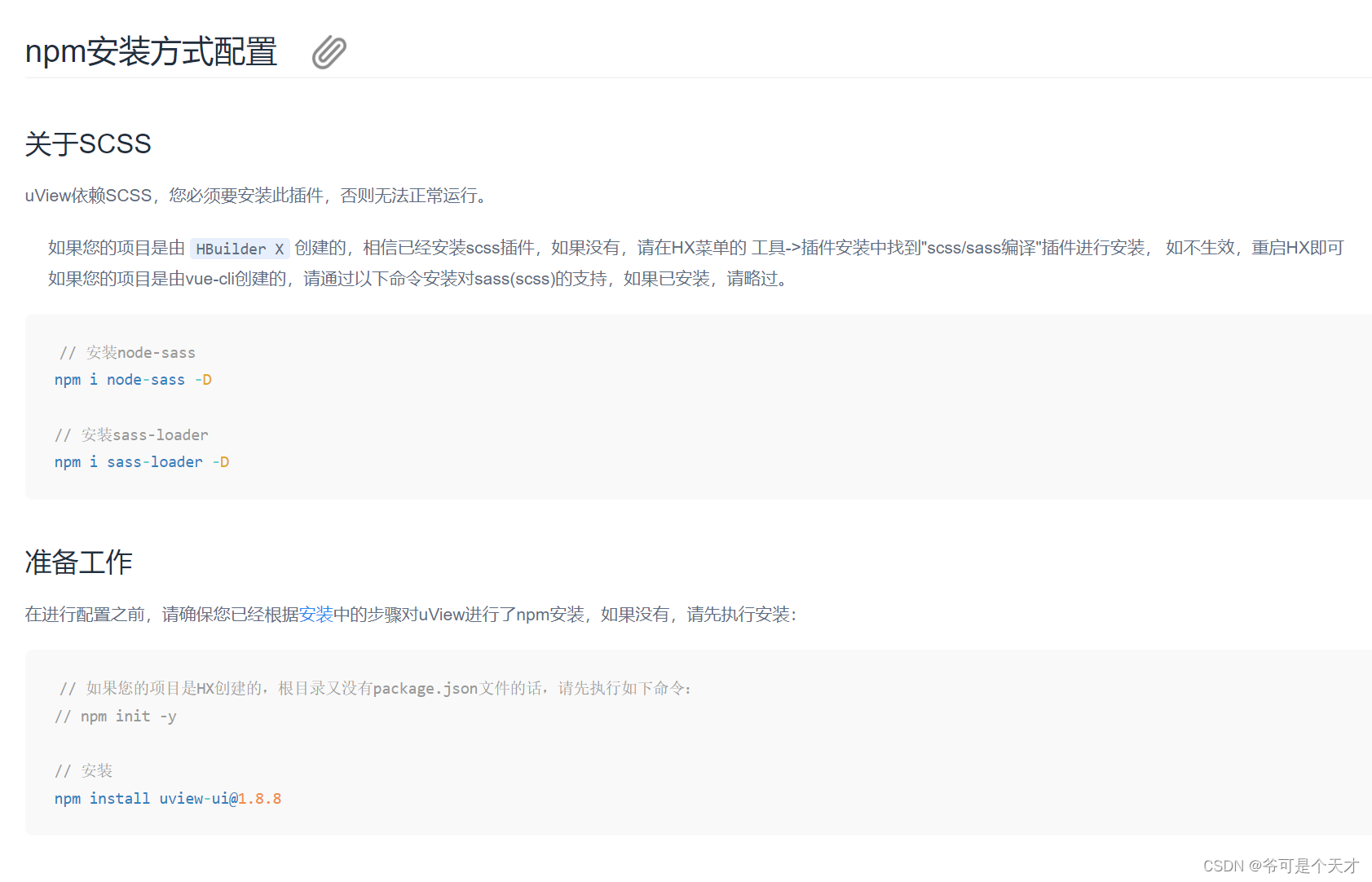
HBuilder创建uniapp默认项目导入uview(胎教)
1:更新HBuilder 建议更新 2:更新插件 我本人在没有更新插件的情况下报错了,找到了**这个大佬**解决问题,所以建议更新插件 先卸载uni-app(Vue2)编译 再重新安装 uni-app(Vue2)…...

C语言基础算法复习
003 斐波那契数列问题 #include<stdio.h> int main() {int i,f11,f21,f3,num;printf("%5d %5d",f1,f2);num2;for(i1; i<18; i){f3f1f2;f1f2;f2f3;num;printf("%5d",f3);if(num%40) printf("\n");}return 0; }//#输数斐波那契数列的前20…...
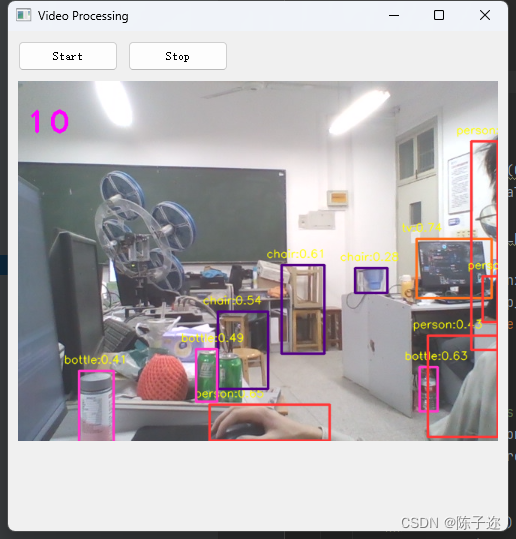
PyQt界面里如何加载本地视频以及调用摄像头实时检测(小白入门必看)
目录 1.PyQt介绍 2.代码实现 2.1实时调用摄像头 2.2 使用YOLOv5推理 2.3 代码中用到的主要函数 1.PyQt介绍 PyQt是一个用于创建桌面应用程序的Python绑定库,它基于Qt框架。Qt是一个跨平台的C应用程序开发框架,提供了丰富的图形界面、网络通信、数据…...
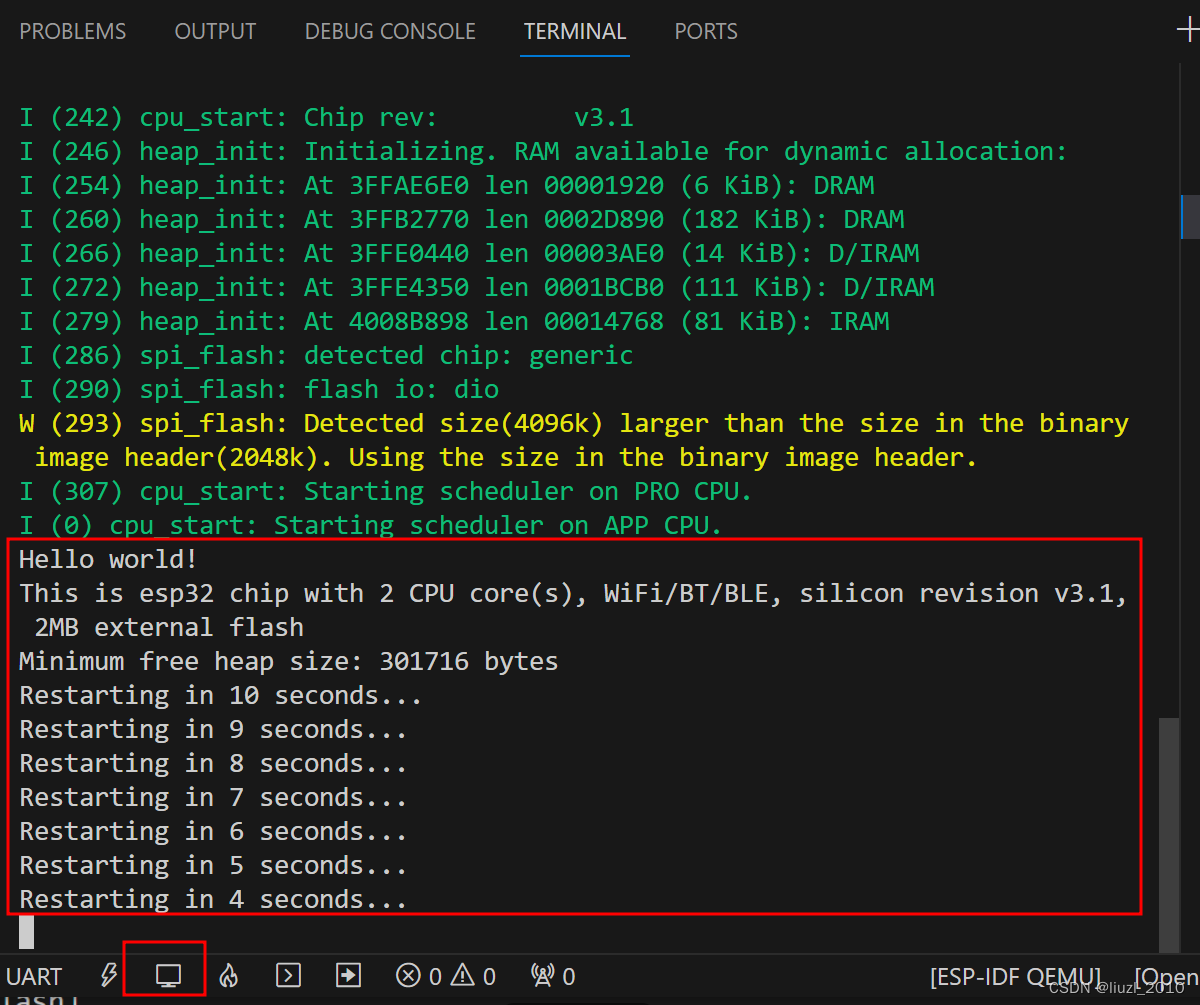
Ubuntu:VS Code IDE安装ESP-IDF【保姆级】
物联网开发学习笔记——目录索引 参考: VS Code官网:Visual Studio Code - Code Editing. Redefined 乐鑫官网:ESP-IDF 编程指南 - ESP32 VSCode ESP-ID Extension Install 一、前提条件 Visual Studio Code IDE安装ESP-IDF扩展&…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
