无重叠区间-力扣435-java贪心策略
一、题目描述
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/non-overlapping-intervals
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
二、运行结果
三、解题思路
这里用的是贪心策略,刚好学习完贪心思想,树上有一道非常类似的题:活动选择。
大致思想就是:先将每个区间按结束时间(第二列)从小到大排列,首先选择第一个区间,然后将与其重叠的区间都移除掉,统计在该区间结束后开始的第一个区间(第一个不和前面的区间重叠的区间),重复进行选择,就可以得到最大不相交子集,总区间的个数减去最大不想交子集中区间的个数就是题目所求的个数。
四、AC代码
class Solution {public int eraseOverlapIntervals(int[][] intervals) {//取出最大不相交子集中区间的个数,总区间个数减去该数就是所求int n = intervals.length;Arrays.sort(intervals, new Comparator<int[]>(){ //按第二列(结束时间)对数组排序public int compare(int[] o1, int[] o2){if(o1[1] == o2[1])return o1[0]-o2[0];return o1[1] - o2[1];}});int count = 1, endTime = intervals[0][1]; for(int i=1; i<n; i++){if(intervals[i][0] >= endTime) { //开始时间在前面的结束时间之后endTime = intervals[i][1];count++;}}return n-count;}
}相关文章:

无重叠区间-力扣435-java贪心策略
一、题目描述给定一个区间的集合 intervals ,其中 intervals[i] [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。示例 1:输入: intervals [[1,2],[2,3],[3,4],[1,3]]输出: 1解释: 移除 [1,3] 后,剩下的区间没有重叠。…...
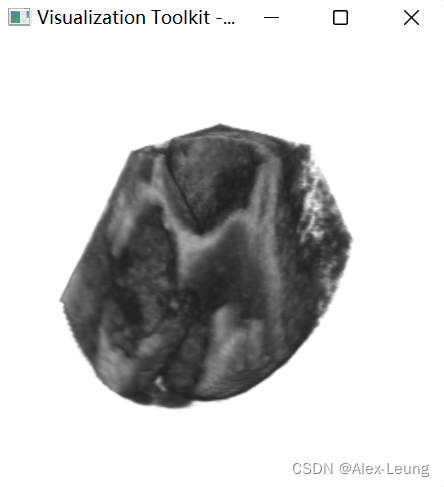
Python使用VTK对容积超声图像进行体绘制(三维重建)
目录VTK简介什么是体绘制?体绘制效果图流程CodeQ&AReferenceVTK简介 VTK(Visualization Toolkit)是一个用于3D计算机图形学、图像处理和可视化的开源软件包。它包括一组C类和工具,可以让用户创建和处理复杂的3D图形和数据可视…...

JAVA设计模式之工厂模式讲解
目录 前言 开始表演 前言 Java中使用工厂模式的主要原因是为了实现代码的灵活性和可维护性。工厂模式是一种创建型设计模式,它提供了一种将对象的创建和使用进行分离的方式。具体来说,工厂模式可以将对象的创建过程封装在一个独立的工厂类中ÿ…...

近万字概述L3及以上自动驾驶故障运行和故障安全机制
本文描述了对ADS的FO和FS机制的评估方法。当系统不能按预期运行时,ADS将使用FO和FS机制。这些机制使ADS能够在最大程度上达到使车辆及其乘员脱离危险的MRC。定义、测试和验证实现MRC的FO和FS策略是确保ADS安全运行和部署的重要步骤。 MRC在SAE J3016中被定义为: 用户或ADS在…...
kafka入门到精通
文章目录一、kafka概述?1.定义1.2消息队列1.2.1 传统消息队列的使用场景1.2.2 消息队列好处1.2.3 消息队列两种模式1.3 kafka基础架构二、kafka快速入门1.1使用docker-compose安装kafka1.2测试访问kafka-manager1.3 查看kafka版本号1.4 查看zookeeper版本号1.5 扩展…...

es-09模糊查询
模糊查询 前缀搜索:prefix 概念:以xx开头的搜索,不计算相关度评分。 注意: 前缀搜索匹配的是term,而不是field。前缀搜索的性能很差前缀搜索没有缓存前缀搜索尽可能把前缀长度设置的更长 语法: GET <ind…...
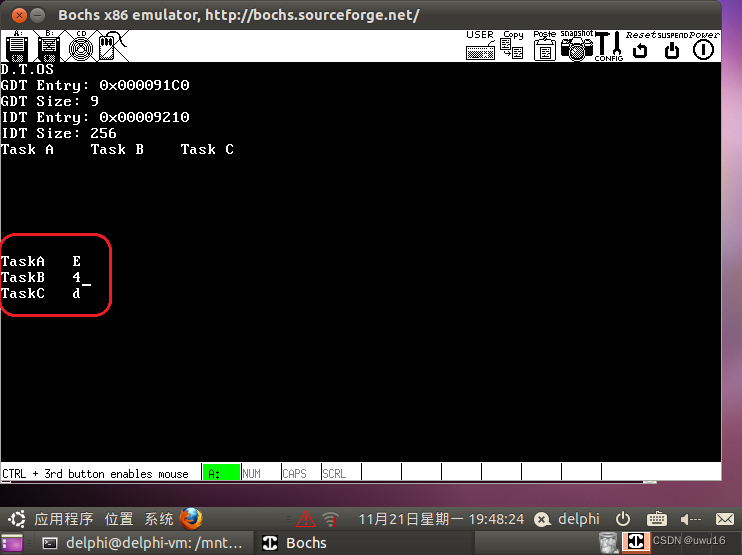
57 - 深入解析任务调度
---- 整理自狄泰软件唐佐林老师课程 文章目录1. 问题1.1 思考1.2 实例分析:问题分析及解决2. 深入讨论2.1 任务调度的定义2.2 关于调度算法的分类2.3 什么时候进行任务调度2.4 任务的分类2.5 关于优先级调度2.6 问题2.7 调度算法的终极目标2.8 课后扩展1. 问题 系统…...

CAN总线开发一本全(3) - 微控制器集成的FlexCAN外设
CAN总线开发一本全(3) - 微控制器集成的FlexCAN外设 苏勇,2023年2月 文章目录CAN总线开发一本全(3) - 微控制器集成的FlexCAN外设引言硬件外设模块系统概要总线接口单元 - 寄存器清单数据结构 - 消息缓冲区MB初始化过…...
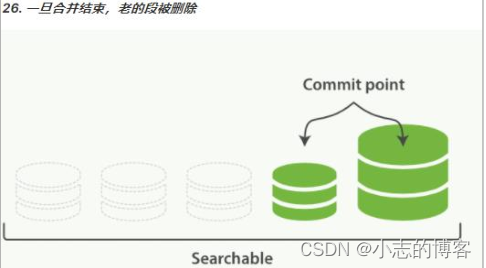
Elasticsearch7.8.0版本进阶——段合并
目录一、段的概述1.1、段的概念1.2、段的缺点1.3、如何解决段数量暴增问题二、段合并的流程三、段合并的注意事项一、段的概述 1.1、段的概念 每一 段 本身都是一个倒排索引。 1.2、段的缺点 由于自动刷新流程每秒会创建一个新的段 ,这样会导致短时间内的段数量…...
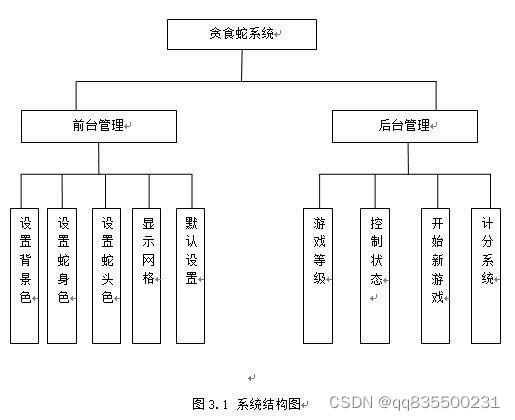
Java版贪食蛇游戏
技术:Java等摘要:近年来Java作为一种新的编程语言,以其简单性、可移植性和平台无关性等优点,得到了广泛地应用,特别是Java与万维网的完美结合,使其成为网络编程和嵌入式编程领域的首选编程语言。MyEclipse是…...

2023年度数学建模竞赛汇总
本人7年数学建模竞赛经验,历史获奖率百分之百。团队成员都是拿过全国一等奖的硕博,有需要数模竞赛帮助的可以私信我。 下面主要列几年一些比较有含金量的数学建模竞赛(按比赛时间顺序) 1. 美国大学生数学建模竞赛 报名时间&…...
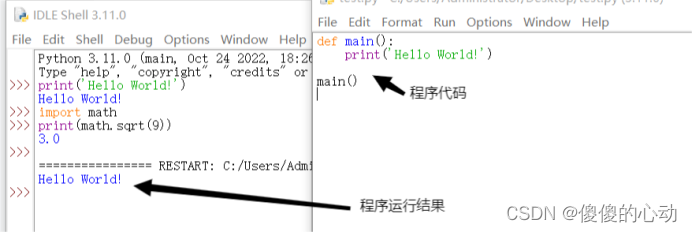
了解Python语言和版本
1.1 任务1了解Python语言和版本 Python 语言的名字来自于一个著名的电视剧"Monty Pythons Flying Cireus",Python之父 Guido van Rossum是这部电视剧的狂热爱好者,所以把他设计的语言命名为Python。 Python 是一门跨平台、开源、免费的解释型高级动态编…...
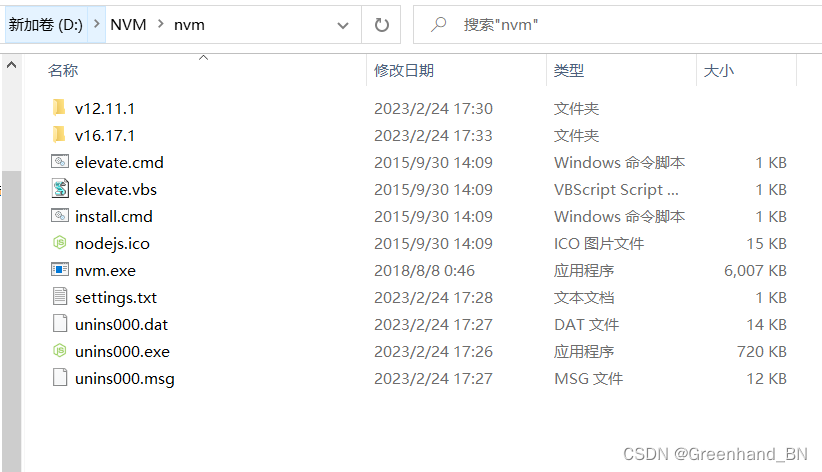
nvm (node版本管理工具)安装的详细步骤,并解决安装过程中遇到的问题
1、下载NVM,跳转下载链接后,如下图,下载红框后解压文件 2、安装 注意:双击安装之后,会有两个地址选择, 1、地址中不能存在空格 2、不要放在C盘中,后面需要改个设置文件,安装到C盘的…...

朴素贝叶斯笔记
贝叶斯公式在A 条件成立下,B的概率等于B的概率*在B条件成立下,A的概率/A的概率,推导假设一个学校中男生占总数的60%,女生占总数的40%。并且男生总是穿长裤,女生则一半穿长裤、一半穿裙子。1.正向概率。随机选取一个学生…...

【GUI】用于电动助力车性能分析的GUI(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

Android:反编译apk踩坑/apktool/dex2jar/JDGUI
需求描述 想要反编译apk文件,搜到了这篇博客:Android APK反编译就这么简单 详解(附图),非常有参考价值~但其中的工具下载链接都已404,而本杂鱼实际操作的过程中也出现了亿点点点点点点的问题,于…...
React 跨域的配置
1、为什么会出现跨域? 浏览器遵循同源政策(同源策略三要素:协议相同、域名相同、端口相同) 2、配置跨域代理 使用中间件 http-proxy-middleware(安装依赖) npm install http-proxy-middleware 创建setupP…...
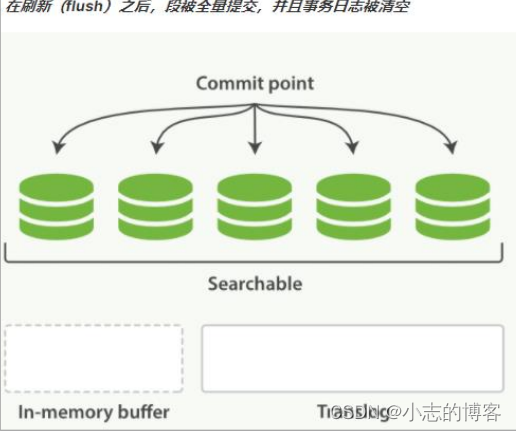
Elasticsearch7.8.0版本进阶——持久化变更
目录一、持久化变更的概述二、事务日志(translog)三、持久化变更完整流程四、事务日志(translog)的作用五、事务日志(translog)的目的一、持久化变更的概述 没有用 fsync 把数据从文件系统缓存刷ÿ…...

CF Edu 127 A-E vp补题
CF Edu 127 A-D vp补题 继续每日一vp,今天晚上有课,时间不太多,回去就直接vp。前三题比较简单,过了之后排名rk2000,然后就去洗澡了。d题没怎么认真思考,其实也可做。最后rk4000。发挥还行,b题罚…...

剑指 Offer 05. 替换空格
摘要 剑指 Offer 05. 替换空格 一、字符替换 由于每次替换从1个字符变成3个字符,使用字符数组可方便地进行替换。建立字符数组地长度为 s 的长度的3倍,这样可保证字符数组可以容纳所有替换后的字符。 获得 s 的长度 length创建字符数组 array&#x…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
