MPNN 模型:GNN 传递规则的实现
首先,假如我们定义一个极简的传递规则
A是邻接矩阵,X是特征矩阵, 其物理意义就是 通过矩阵乘法操作,批量把图中的相邻节点汇聚到当前节点。
但是由于A的对角线都是 0.因此自身的节点特征会被过滤掉。
图神经网络的核心是 吸周围之精华,再叠加自身,因而需要改进来保留自身特征。如何做?
方法是给每个节点添加一个自环,即将邻接矩阵对角线值各加1,此时用表示,
做到了聚合邻居节点并保留自身信息。
但是当图过于复杂时,聚合邻居信息会不断执行矩阵乘法或加法,可能导致特征值太大而溢出。如何做?
方法是邻接矩阵归一化。那么如何归一化呢?我们由A可以得到图的度D,由于A变成了,我们认为
的度为
。常用的归一化方式就是用度数矩阵的倒数
。
则
但是仅仅对矩阵A进行了列上的缩放,操作后的元素值是不对称的,某种程度破坏了图结构的对称性。(这是为什么?)那么如何修复这种对称性呢?
方法是在行的方向上也进行对等缩放,具体 做法是,让邻接矩阵右乘一个缩放因子
,这样就使得缩放版本的邻接矩阵重新恢复对称性。于是信息聚合的方式为
能够很好地缩放邻接矩阵,既然-1次幂可以完成,为什么不尝试一下(-1/2)次幂呢?
事实上,对每个矩阵元素都实施
这种操作可以对邻接矩阵地每一行每一列”无偏差“地进行一次归一化,以防相邻节点间度数不匹配对归一化地影响。(why)?
于是就出现了被众多学术论文广泛采纳地邻接矩阵地缩放形式
考虑权值影响的信息聚合
上述仅仅考虑到邻接矩阵对获取邻居节点信息的影响,即只考虑拓扑结构施加的影响。事实上,对于特定节点而言,不同维度的特征值对给定任务的影响程度是不同的,如果第对各个特征值进行时 打分就,就要涉及到权值矩阵W了,也就是要构造更为完整的图神经网络模型 AWX。权值矩阵W通常是通过学习得到的。
如果我们想压缩节点输出的维度,也可以缩减权值矩阵的输出维度。
在以上的分析中,没有考虑激活函数的影响,无法给予神经网络的非线性变换能力,因此通常我们需要使用sigmoid、tanh、Relu等作为激活函数,最后再用argmax函数模拟一个分类的输出。
reference:
《从深度学习到图神经网络:模型与实践》 张玉宏 等
code:
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np#定义节点
N = [(f"v{i}", 0) for i in range (1,3)] + [(f"v{i}",1) for i in range (3,5)] + [(f"v{i}",2) for i in range (5,6)] #定义节点#定义边
E = [("v1","v2"),("v1","v3"),("v2","v1"),("v2","v3"),("v2","v4"),("v3","v1"),("v3","v2"),("v3","v4"),("v4","v2"),("v4","v3"),("v4","v5"),("v5","v4")] #定义边G = nx.Graph() #构造图G.add_nodes_from(list(map(lambda x: x[0],N))) #给图添加节点
G.add_edges_from(E) #给图添加边ncolor =['r']*2 + ['b']*2 +['g']*1 #设置节点颜色
nsize = [700]*2 + [700]*2 + [700]*1 #设置节点的大小#显示图
nx.draw(G, with_labels= True, font_weight ='bold', font_color = 'w', node_color =ncolor, node_size =nsize)
plt.show()#借用nx构造邻接矩阵
A = np.array(nx.adjacency_matrix(G).todense())
print(A)#构造特征矩阵X
X = np.array([[i,-i, i+2] for i in range (A.shape[0])])
print(X)#为了不丢失自己的属性,需要修改本身的邻接矩阵,因为最初邻接矩阵的斜对角线为0
I = np.eye(A.shape[0])
A_hat = A + I
print('A_hat')
print(A_hat)#计算自环邻接矩阵的度
D_hat = np.diag(np.sum(A_hat,axis= 0 ))
print(D_hat)#获取D——hat的逆矩阵,即一个缩放因子
D_1 = np.diag(D_hat) ** (-1) *np.eye(A_hat.shape[0])
print('D_1')
print(D_1)#缩放版的邻接矩阵
A_scale = D_1 @ A_hat #对矩阵A仅仅进行了列方向上的缩放
print('A_scale')
print(A_scale)#用A_scale来聚合邻居节点的信息
X_new = A_scale @ X
print('X_new')
print(X_new)#修复原本的缩放的不对称性
scale_factor = D_1 @ A_hat @ D_1 #scale_factor 是对称的,而 A_scale是不对称 的
print('scale_factor')
print(scale_factor)#用scale_factor来聚合邻居节点的信息
X_new1 = scale_factor @ X
print('X_new1')
print(X_new1)D_sq_half = np.diag(D_hat) ** (-0.5) *np.eye(A_hat.shape[0])
print('D_sq_half')
print(D_sq_half)#修复原本的缩放的不对称性
scale_factor2 = D_sq_half @ A_hat @ D_sq_half #scale_factor 是对称的,而 A_scale是不对称 的
print('scale_factor2')
print(scale_factor2)#用scale_factor2来聚合邻居节点的信息
X_new2 = scale_factor2 @ X
print('X_new2')
print(X_new2)#给出的权值矩阵
W = np.array([[0.13,0.24],[0.37,-0.32],[0.14,-0.15]])X_new3 = X_new2 @ W
print(X_new3)#也可以缩减W的尺寸压缩节点的输出维度
W1 = np.array([[0.13],[0.37],[0.14]])
#计算logits
logits = X_new2 @ W1
print(logits)#以上都没有考虑到激活函数,无法模拟神经网络的非线性变换能力,可以使用激活函数
y = logits * (logits >0) #使用Relu函数
print(y)#为了实现分类等功能,还需要添加一层Softmax
def softmax(x):return np.exp(x) /np.sum(np.exp(x), axis = 0)prob = softmax(y)
print('y')
print(y)#模拟一个分类输出
pred = np.argmax(prob)
print(pred)相关文章:
MPNN 模型:GNN 传递规则的实现
首先,假如我们定义一个极简的传递规则 A是邻接矩阵,X是特征矩阵, 其物理意义就是 通过矩阵乘法操作,批量把图中的相邻节点汇聚到当前节点。 但是由于A的对角线都是 0.因此自身的节点特征会被过滤掉。 图神经网络的核心是 吸周围…...

Flink kafka 数据汇不指定分区器导致的问题
背景 在flink中,我们经常使用kafka作为flink的数据汇,也就是目标数据的存储地,然而当我们使用FlinkKafkaProducer作为数据汇连接器时,我们需要注意一些注意事项,本文就来记录一下 使用kafka数据汇连接器 首先我们看…...

【软考】14.1 面向对象基本概念/分析设计测试
《面向对象开发》 对象 现实生活中实际存在的一个实体;构成系统的一个基本单位由对象名、属性和方法组成 类 实体的形式化描述;对象是类的实例,类是对象的模板可分为:实体类:现实世界中真实的实体接口类(边…...
MFC-对话框
目录 1、模态和非模态对话框: (1)、对话框的创建 (2)、更改默认的对话框名称 (3)、创建模态对话框 1)、创建按钮跳转的界面 2)、在跳转的窗口添加类 3࿰…...

Essential Steps in Natural Language Processing (NLP)
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
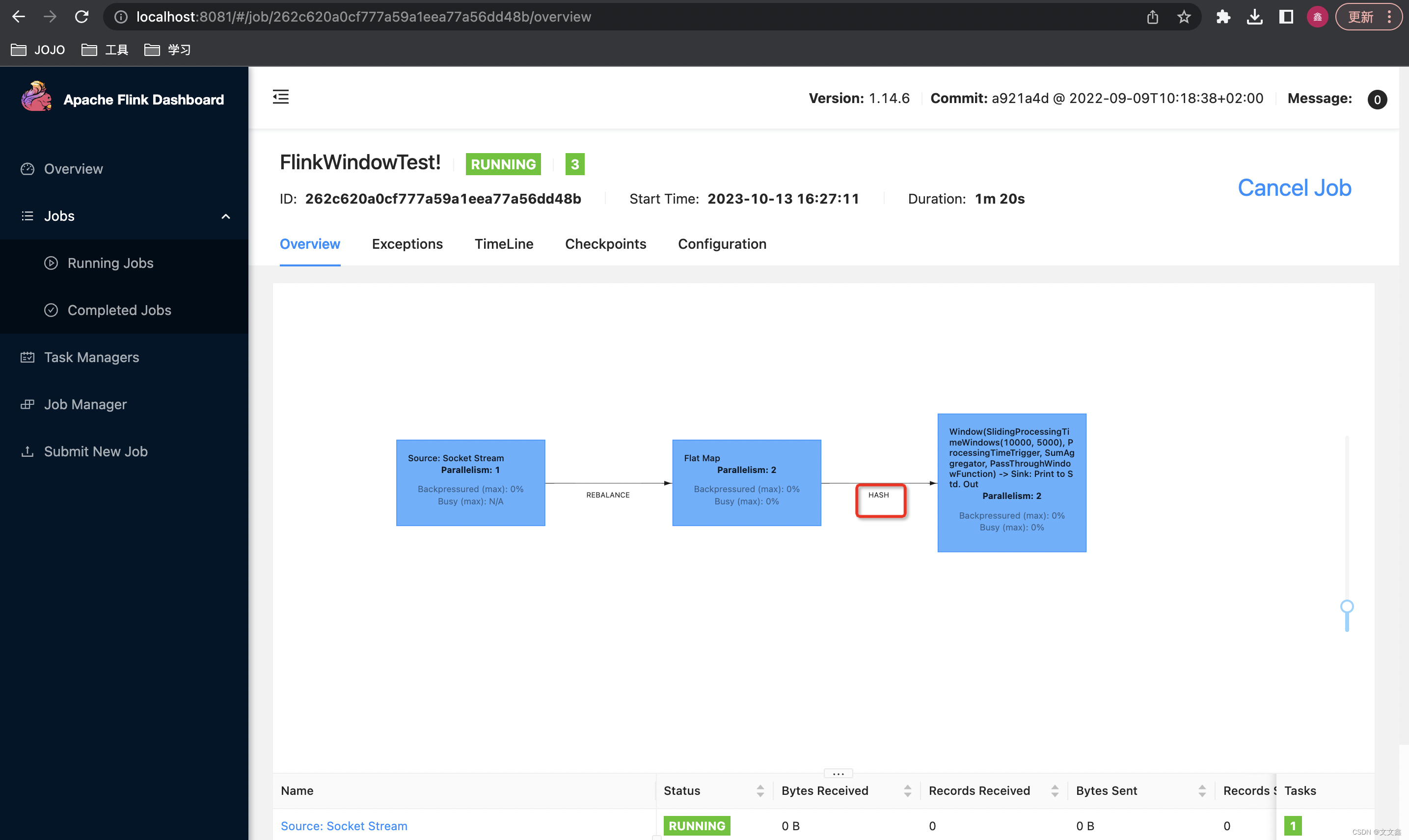
Flink中KeyBy、分区、分组的正确理解
1.Flink中的KeyBy 在Flink中,KeyBy作为我们常用的一个聚合类型算子,它可以按照相同的Key对数据进行重新分区,分区之后分配到对应的子任务当中去。 源码解析 keyBy 得到的结果将不再是 DataStream,而是会将 DataStream 转换为 Key…...
QT6集成CEF3--01 准备工作
QT6集成CEF3--01 准备工作 一、所有使用到的工具软件清单:二、准备工作三、cefclient示例程序四、特别注意 一、所有使用到的工具软件清单: CEF 二进制发行包 cef_binary_117.2.5gda4c36achromium-117.0.5938.152_windows64.tar.bz2 CMake 编译工具 cmake-3.22.6-windows-x86_…...

随机误差理论与测量
文章目录 第1节 随机误差的性质和特点第2节 随机误差的数字特性标准差的估计 第3节 单次测量结果的精度指标第4节 多次测量结果的精度指标算数平均值的分布特性与标准差算数平均值的置信度算数平均值的精度指标(常用的有4个) 第5节 非等精度测量 第1节 随机误差的性…...
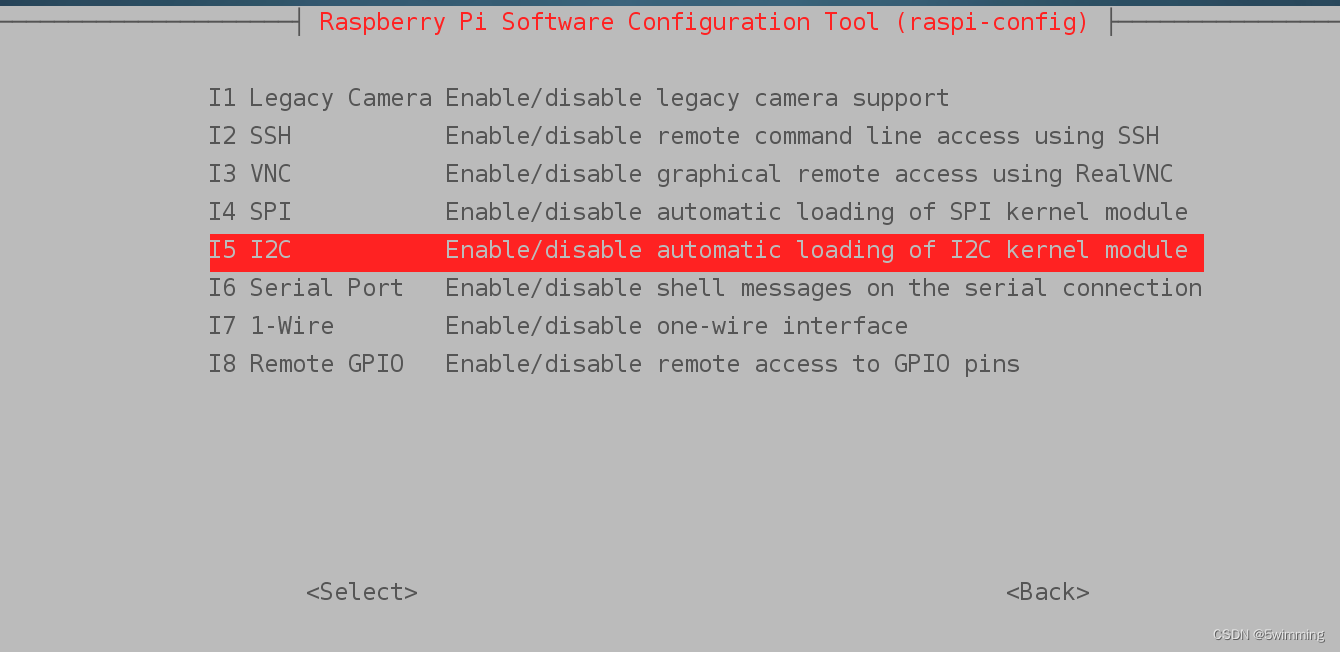
树莓派4b配置通过smbus2使用LCD灯
出现报错: FileNotFoundError: [Errno 2] No such file or directory: ‘/dev/i2c-1’ 则说明没有打开I2C,可通过如下步骤进行设置 1、打开树莓派配置 sudo raspi-config2、进入Interface Options,配置I2C允许 目前很多python3版本已经不…...

UPS 原理和故障案例分享
摘要:不间断电源UPS (Uninterruptible Power System),主要是由整流器、 逆变器、静态旁路和储能装置等组成;具备高可靠性、高可用性和高质量的独立 电源。通过对收集的 UPS 故障案例进行分析,从施工,调试和运行三个方面筛选 出四个故障案例与…...

Stream流中的 max()和 sorted()方法
需求:某个公司的开发部门,分为开发 一部 和 二部 ,现在需要进行年中数据结算。分析: 员工信息至少包含了(名称、性别、工资、奖金、处罚记录)开发一部有 4 个员工、开发二部有 5 名员工分别筛选出 2 个部门…...
云上攻防-云原生篇Docker安全权限环境检测容器逃逸特权模式危险挂载
文章目录 前言1、Docker是干嘛的?2、Docker对于渗透测试影响?3、Docker渗透测试点有那些?4、前渗透-判断在Docker中方式一:查询cgroup信息方式二:检查/.dockerenv文件方式三:检查mount信息方式四࿱…...

PDE数值解中,为什么要引入弱解(weak solution)的概念?
See https://www.zhihu.com/question/24243246?utm_sourceqq&utm_mediumsocial&utm_oi1315073218793488384...

使用pdfjs实现在线预览pdf
在工作中可能会遇到前端展示pdf文件进行预览并提供下载的需求场景,例如操作指引,这个时候需要寻找一款实现该功能的插件,以pdjjs举例子 1. 安装pdf.js npm install pdfjs-dist2. 引入pdf.js import pdfjsLib from pdfjs-dist3.加载pdf文件流 这个地方区分是请求后端接口还是…...
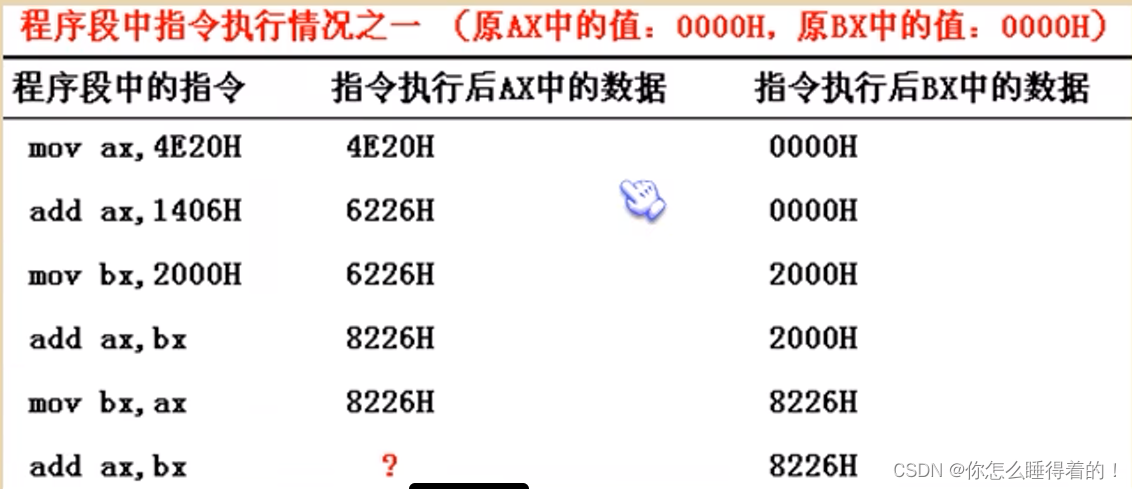
汇编语言基础
引言 汇编语言是直接在硬件之上工作的编程语言,首先要了解硬件系统的结构,才能有效的应用汇编语言对其编程。汇编课程的研究重点放在如何利用硬件系统的编程结构和指令集有效灵活的控制系统进行工作。 基础知识 1.1机器语言 机器语言是机器指令的集合…...
格式工厂怎么把两个视频合并在一起
免费的工具谁不喜欢呢,今天为大家介绍的是格式工厂这款多功能视频转换软件,然而今天主要为大家介绍的是格式工厂的视频合并功能。 是的,你没有听错,格式工厂除了转换之外,还可以视频合适、视频剪辑、视频分割、去水印…...
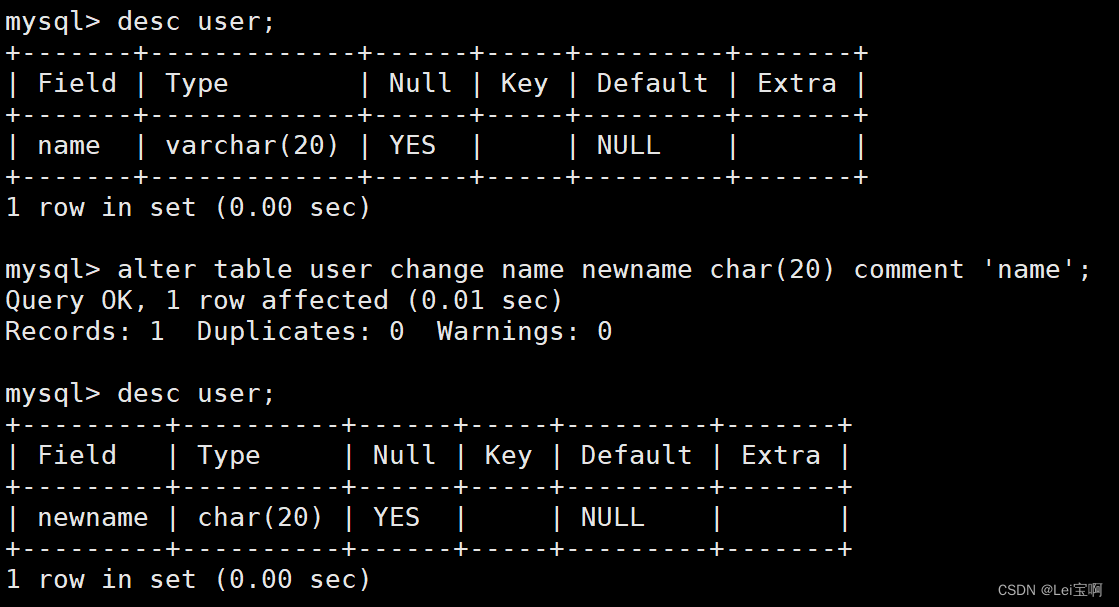
2.MySQL表的操作
个人主页:Lei宝啊 愿所有美好如期而遇 表的操作 (1)表的创建 CREATE TABLE table_name ( field1 datatype, field2 datatype, field3 datatype ) character set 字符集 collate 校验规则 engine 存储引擎; 存储引擎的不同会导致创建表的文件不同。 换个引擎。 t…...

网络安全之应急流程
近期需要弄一个网络安全应急的流程,其实对于网络安全应急并不陌生,只是在一些特定的环境上会遇到一些难以解决的问题或者缺少某个岗位的技术人员,因为不同运营商的应急小队也是不同的岗位,如今有着安全设备的告警和预警࿰…...

[Python进阶] 操纵鼠标:pyuserinput
6.2 操纵鼠标:pyuserinput 6.2.1 说明 在安装pyuserinput库时会自动安装PyMouse和PyKeyboard库。前者主要用来操作鼠标,包括鼠标的点击、移动等。后者主要用来操作键盘,包括键盘按键的按下、弹起等。 这两个库还可以同时对鼠标和键盘的事件…...
【LeetCode】每日一题两数之和寻找正序数组的中位数找出字符串中第一个匹配项的下标在排序数组中查找元素的第一个和最后一个位置
主页点击直达:个人主页 我的小仓库:代码仓库 C语言偷着笑:C语言专栏 数据结构挨打小记:初阶数据结构专栏 Linux被操作记:Linux专栏 LeetCode刷题掉发记:LeetCode刷题 算法:算法专栏 C头…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
