C++算法:前缀和基础
相关
源码测试用例下载
https://download.csdn.net/download/he_zhidan/88430716 包括4个压缩包,初始代码,实现前缀和,实现前缀积,实现前缀异或。都是在前者的基础上修改的。
本博文是CSDN学院课程的讲义
https://edu.csdn.net/course/detail/38771
前缀和(前缀积、前缀异或)应用的博文
C++前缀和算法:构造乘积矩阵
原理
长度为n的数组nums,共有n+1个以nums[0]开始的子数组。索引范围分别为[0,i),i取值区间[0,n]。preSum[i]记录子数组[0,i)的和。比如:nums = {1,2,3,4},则preSum = {0,1,3,6,10}。通过preSum,我们可以求任意nums的子数组和。子数组[i,j)等于子数组[0,j)减去[0,i),也就是子数组[i,j)的和等于preSum[j] – preSum[i]。如果i等于j,则preSum[i]-preSum[i],和为0,符合计算公式。如果i大于j,则非法,需要提前排除。
暴力法
时间复杂度O(n*n)。
核心代码
class CPreSum
{
public:
//左闭右开空间
long long SumO2(int left, int r)
{
long long llRet = 0;
for (; left < r; left++)
{
llRet += m_sums[left];
}
return llRet;
}
vector m_sums;
};
测试代码
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
assert(v1[i] == v2[i]);
}
}
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
void Test1()
{
CPreSum preSum;
preSum.m_sums = { 1,2,3,4 };
vector ans = { 0,1,3,6,10 };
auto res = preSum.SumO2(0, 4);
Assert(10LL, res);
res = preSum.SumO2(0, 3);
Assert(6LL, res);
res = preSum.SumO2(0, 2);
Assert(3LL, res);
res = preSum.SumO2(0, 1);
Assert(1LL, res);
res = preSum.SumO2(0, 0);
Assert(0LL, res);
res = preSum.SumO2(1, 4);
Assert(9LL, res);
res = preSum.SumO2(1, 3);
Assert(5LL, res);
}
void Test2()
{
srand(time(nullptr));
int n = rand() % 10 + 1;
CPreSum preSum;
for (int i = 0; i < n; i++)
{
preSum.m_sums.emplace_back(rand() % 10000);
}
preSum.Init();
for (int left = 0; left < n; left++)
{
for (int r = left; r <= n; r++)
{
long long res1 = preSum.SumO1(left, r);
long long res2 = preSum.SumO2(left, r);
assert(res1==res2);
}
}
}
int main()
{
Test1();
Test2();
}
前缀和
时间复杂度O(n),预处理O(n),每次查询O(1)。
代码
void Init()
{
m_vPreSum.emplace_back(0);
for (const auto& n : m_nums)
{
m_vPreSum.emplace_back(n + m_vPreSum.back());
}
}
long long SumO1(int left, int r)
{
return m_vPreSum[r] - m_vPreSum[left];
}
vector m_vPreSum;
前缀乘积
只需要修改三处m_vPreSum[0]=1,+变成*,-变成除。
修改后的代码
class CPreSum
{
public:
//左闭右开空间
long long SumO2(int left, int r)
{
long long llRet = 1;
for (; left < r; left++)
{
llRet *= m_nums[left];
}
return llRet;
}
void Init()
{
m_vPreSum.emplace_back(1);
for (const auto& n : m_nums)
{
m_vPreSum.emplace_back(n * m_vPreSum.back());
}
}
long long SumO1(int left, int r)
{
return m_vPreSum[r] / m_vPreSum[left];
}
vector m_vPreSum;
vector m_nums;
};
前缀异或
C语言异或的符合是,初始0,也就是m_vPreSum.emplace_back(0)。异或的逆运算是本身,所以乘除都换成。

其它
视频课程
要是你认为本篇难道较大,不好入手,推荐你先学习基础算法的课程,我已完成部分,余下部分持续更新中,就在CSDN学院。
https://edu.csdn.net/course/detail/38771
C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
相关下载
如果你想观其大略,建设下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 博主想队大家说的话 |
|---|
| 墨家名称的来源:有所得以墨记之。 |
| 闻缺陷则喜的来由:早发现,早修改问题,成本更低 |
| 程序是龙,算法是睛 |

相关文章:

C++算法:前缀和基础
相关 源码测试用例下载 https://download.csdn.net/download/he_zhidan/88430716 包括4个压缩包,初始代码,实现前缀和,实现前缀积,实现前缀异或。都是在前者的基础上修改的。 本博文是CSDN学院课程的讲义 https://edu.csdn.net/c…...

vue和react的区别
目录 1. 数据绑定 Vue React 2. 组件化 Vue React 3. 学习曲线 4. 状态管理 Vue React 5. 社区和生态系统 3. 学习曲线 4. 状态管理 Vue React 5. 生态系统 6. 社区和支持 7. 性能 8. 生产环境性能 9.语法和模板: 结论 当涉及到前端开发框架时,…...

STM32 之 HAL 库串口 USART 丢数据及ORE卡死的解决方案
STM32 之 HAL 库串口 USART 丢数据及ORE卡死的解决方案_hal_uart_error_ore-CSDN博客...
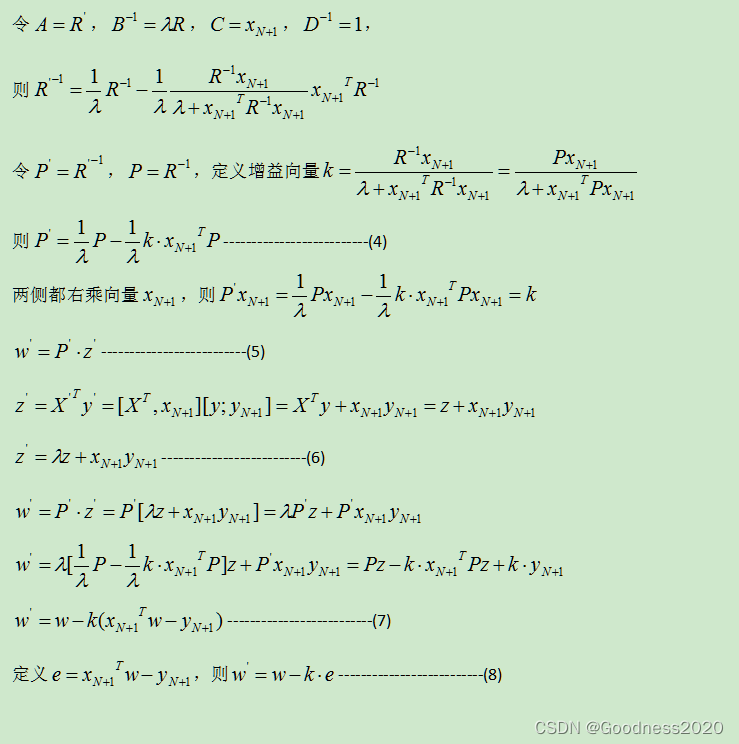
递归最小二乘法RLS
参考:RLS递归最小二乘法(Recursive Least Squares)_hymwgk的博客-CSDN博客...

Apache Doris (三十九):Doris数据导出 - MySQL dump导出
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹哥教你大数据个人主页-哔哩哔哩视频 目录...
【Nginx32】Nginx学习:随机索引、真实IP处理与来源处理模块
Nginx学习:随机索引、真实IP处理与来源处理模块 完成了代理这个大模块的学习,我们继续其它 Nginx 中 HTTP 相关的模块学习。今天的内容都比较简单,不过最后的来源处理非常有用,可以帮我们解决外链问题。另外两个其实大家了解一下就…...

vue3后台管理框架之集成sass
我们目前在组件内部已经可以使用scss样式,因为在配置styleLint工具的时候,项目当中已经安装过sass sass-loader,因此我们再组件内可以使用scss语法!!!需要加上lang="scss" <style scoped lang="scss"></style> 接下来我们为项目添加一些…...

无需付费开会员,一个Python程序实现PDF转高清图片
今天需要将一个PDF导出为图片,但是一般的在线转换网站导出的图片清晰度都不高,分辨率只有1241*1754,这就导致输出的图片放大后字体是有点模糊的,所以就想到了使用Python中的PyPDF2库来处理PDF文件,以及Pillow库来处理图…...
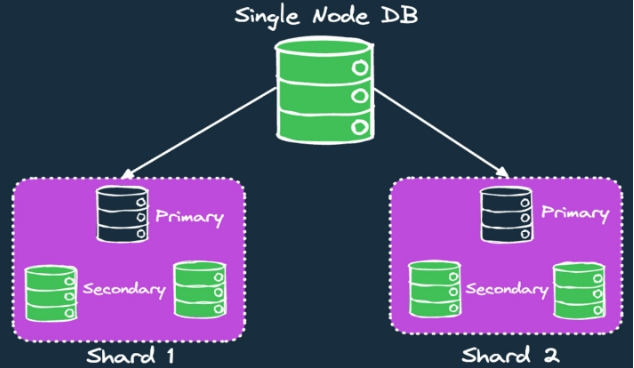
为分布式系统设计数据库
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 数据库设计是微服务和云原生解决方案的关键因素,因为基于微服务的架构导致了数据的分布式。数据管理不再在一个单一的过程中发生,而是可以通过多…...

Programming abstractions in C阅读笔记:p179-p180
《Programming Abstractions In C》学习第60天,p179-p180总结。 一、技术总结 1.palindrome(回文) (1)包含单个字符的字符串(如"a"),或者空字符串(如" ")也是回文。 (2)示例:“level”、“noon”。 2.predicate fun…...
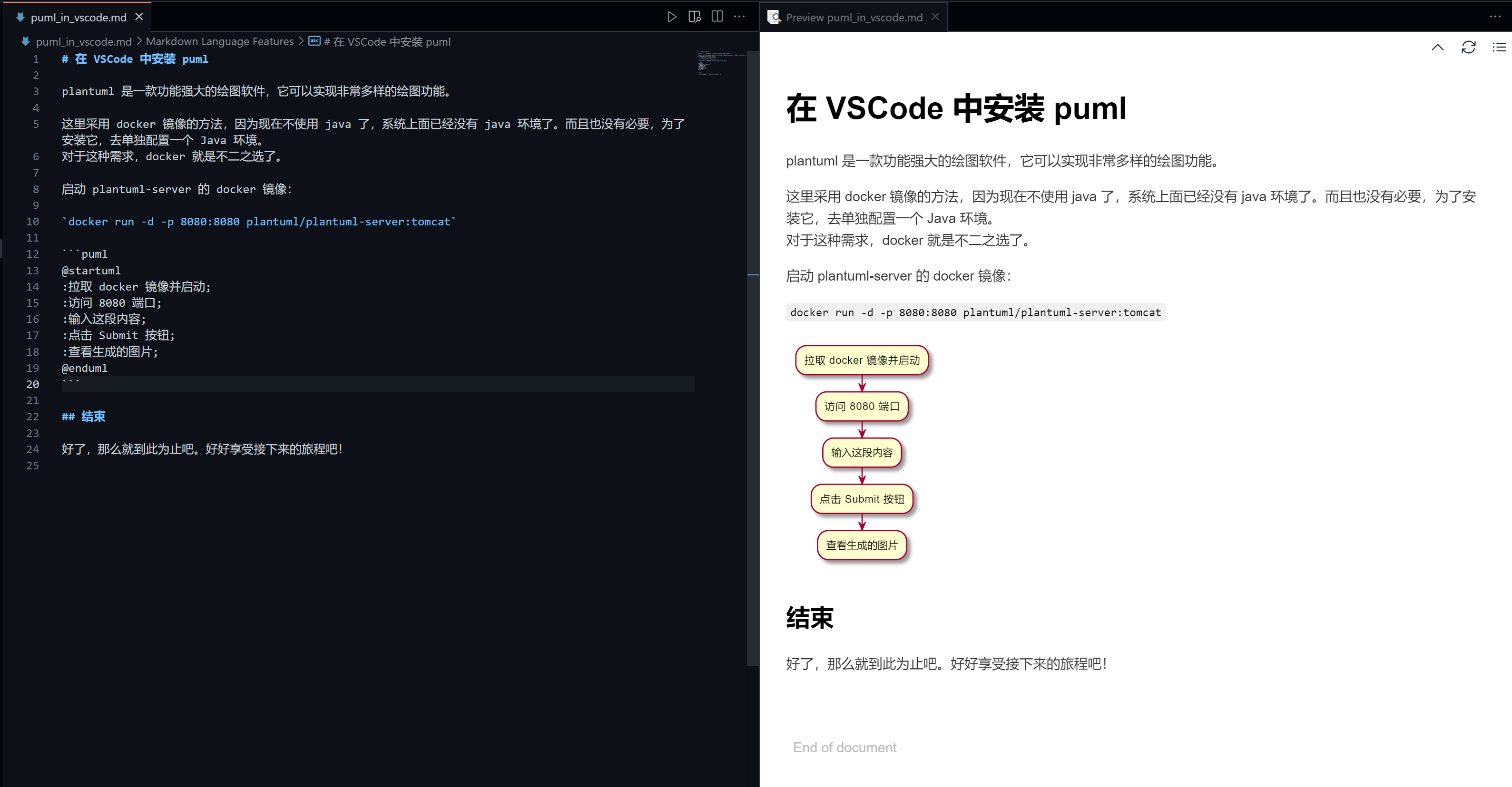
在 VSCode 中使用 PlantUML
最近,因为工作需要绘制一些逻辑图,我自己现在使用的是 PlantUML 或者 mermaid,相比之下前者更加强大。不过它的环境也麻烦一些,mermaid 在一些软件上已经内置了。但是 PlantUML 一般需要自己本地安装或者使用远程服务器࿰…...

css3过渡属性属性名:transition
CSS3的过渡属性属性名是transition,它允许我们在状态改变时为元素添加过渡效果,例如在元素从一种样式变为另一种样式时添加平滑的过渡效果。 transition的语法如下: transition: property duration timing-function delay;其中,…...
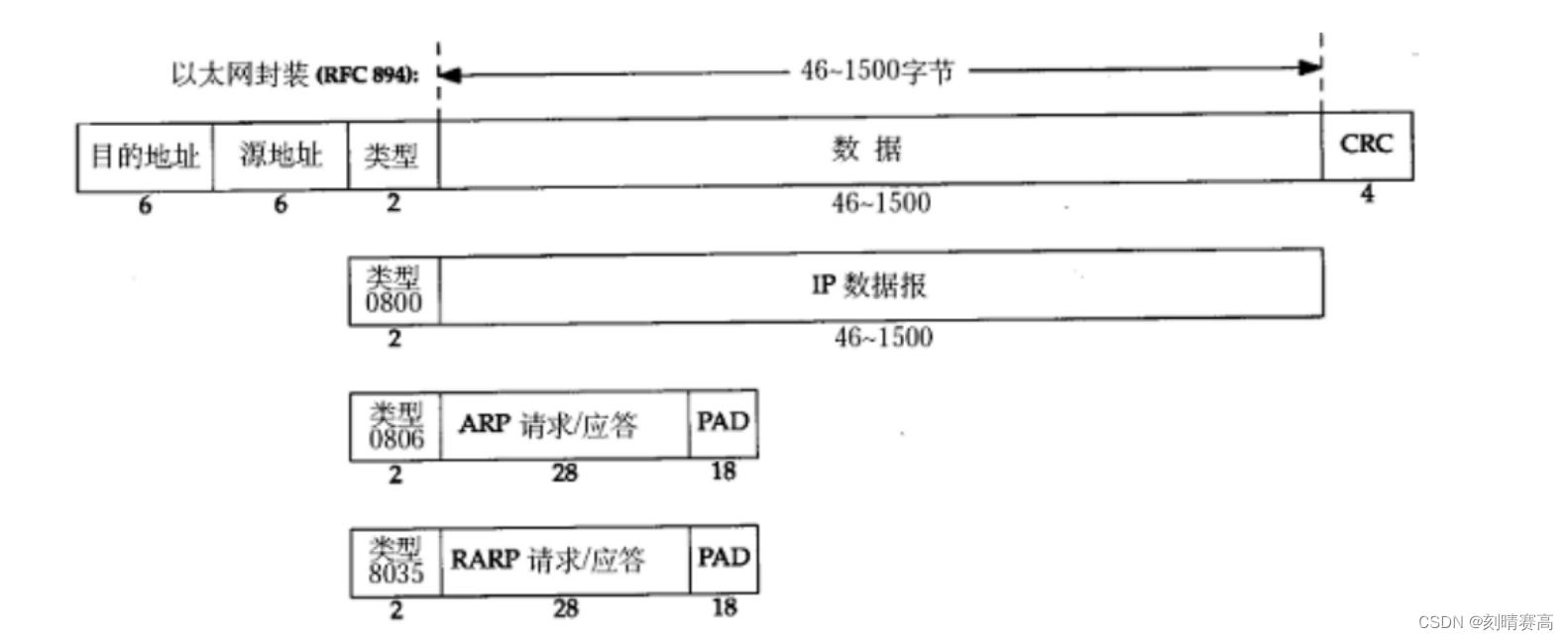
关于数据链路层(初步)
以太网帧格式: 源地址和目的地址是指网卡的硬件地址(也叫MAC地址),长度是48位,是在网卡出厂时固 化的; 帧协议类型字段有三种值,分别对应载荷的形式,有IP、ARP、RARP; …...
诊断DLL——CAPL_DLL集成安全访问算法
文章目录 前言一、CAPL DLL简介DLL生成C2338报错解决方案:二、添加27服务解锁算法三、CAPL调用dll前言 在实际诊断工程应用中,如UDS刷写——27服务,经常会遇到一些Seed2Key的算法问题,为了安全保密,这个算法的源码不便公开,我们可以将其打包成DLL,然后在CANoe诊断控制面…...
)
集合元素处理(传统方式和Stream方式)
1、集合元素处理(传统方式) 现在有两个ArrayList集合存储队伍当中的多个成员姓名,要求使用传统的for循环(或增强for循环)依次进行一下若干操作步骤: 第一个队伍只要 名字为 3 个字 的成员姓名;存…...

亲测好用,这3款免费高清录屏软件,效果惊人!
在当今社会上,录屏软件已经成为了人们日常生活中不可或缺的一部分。无论是在工作还是学习中,我们都需要使用录屏软件来录制屏幕上的内容。然而,许多录屏软件都是收费的,这对于那些想要尝试录屏软件但又不想花钱的人来说࿰…...

超声波清洗机洗眼镜真的可以洗干净吗?眼镜超声波清洗机推荐
截止2023年4月份近视眼的统计,我过近视人群高达3亿人,可想而知现在近视的群体是有多么庞大的。近视就免不了要戴眼镜,但是一副眼镜长时间的佩戴不清洗的话,镜片会不清晰,也有的朋友会眼镜脏了就去配一副新的࿰…...

centos7安装部署ElasticSearch
文章目录 ElasticSearch安装部署简介安装卸载 ElasticSearch安装部署 简介 全文搜索属于最常见的需求,开源的 Elasticsearch (以下简称 es)是目前全文搜索引擎的首选。 它可以快速地储存、搜索和分析海量数据。维基百科、Stack Overflow、G…...

websocket+node+vite(vue)实现一个简单的聊天
1.前端逻辑 本项目基于之前搭建的vite环境:https://blog.csdn.net/beekim/article/details/128083106?spm1001.2014.3001.5501 新增一个登录页和聊天室页面 <template><div>登录页</div><div>用户名:<input type"text" pl…...
YApi和Swagger接口管理
这篇博客针对苍穹外卖而写 YApi 之前的官网:yapi.smart-xwork.cn 由于之前的网址访问不了,现在我用的是这个网址:YApi Pro-高效、易用、功能强大的可视化接口管理平台 登录之后如下 创建两个工作空间 用户端接口也是如法炮制 Swagger 使用…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
