阿里云服务器ECS实例规格族c/g/r等字母说明
阿里云服务器ECS实例命名规则:ecs.<规格族>.large字母含义命名说明,包括x86、ARM架构、GPU异构计算、弹性裸金属、超级计算集群SCC云服务器,c代表计算型、g代表通用型、r代表内存型、u代表通用算力型、e代表经济型e实例,阿里云百科aliyunbaike.com分享阿里云服务器ECS实例规格字母命名含义详细说明:
目录
云服务器ECS实例规格字母含义命名说明
x86计算规格族和ARM计算规格族
异构计算规格族、弹性裸金属服务器、超级计算集群(SCC)实例规格族
云服务器ECS实例规格字母含义命名说明
阿里云服务器ECS架构分为X86计算、ARM计算、GPU/FPGA/ASIC、弹性裸金属服务器、超级计算集群,如下图:

阿里云服务器ECS实例计算架构
常见的云服务器ECS规格有计算型c7、通用型g7、通用算力型u1和经济型e实例等,为什么叫这个名字呢?这些字母是有含义的:
实例规格族名称格式为ecs.<规格族>,实例规格名称为ecs.<规格族>.large:
- ecs:云服务器ECS的产品代号
- <规格族>:由规格族主体+规格族后缀组成
- 阿里云CLUB中心:aliyun.club 领取专属代金券
x86计算规格族和ARM计算规格族
| 命名组成 | 说明 | 命名示例含义,阿里云百科 |
|---|---|---|
| 规格族主体 | 由小写字母+数字组成。
|
例如,ecs.g6.2xlarge表示通用型g6规格族中的一个实例规格,拥有8个vCPU核。相比于g5规格族,g6为新一代通用型实例规格族。 |
| 规格族后缀 | 由小写字母组成。 |
|
异构计算规格族、弹性裸金属服务器、超级计算集群(SCC)实例规格族
异构计算规格族、弹性裸金属服务器和超级计算集群(SCC)实例规格族一般采用自主命名方式,由小写字母和数字混合组成。
| 命名组成 | 说明 | 命名示例含义 |
|---|---|---|
| 规格族主体 | 由小写字母组成。 |
|
| 规格族后缀 | 由数字或小写字母+数字组成。 |
|
large:large表示vCPU核数,中的n越大,表示vCPU核数越多。其中,xlarge代表4核,2xlarge代表8核,3xlarge代表12核等等,以此类推。
以上是阿里云百科分享的关于阿里云服务器ECS命名规则。
相关文章:

阿里云服务器ECS实例规格族c/g/r等字母说明
阿里云服务器ECS实例命名规则:ecs.<规格族>.large字母含义命名说明,包括x86、ARM架构、GPU异构计算、弹性裸金属、超级计算集群SCC云服务器,c代表计算型、g代表通用型、r代表内存型、u代表通用算力型、e代表经济型e实例,阿里…...

Everything和SVN结合使用-在Everything中显示SVN
点击跳转>Unity3D特效百例点击跳转>案例项目实战源码点击跳转>游戏脚本-辅助自动化点击跳转>Android控件全解手册点击跳转>Scratch编程案例点击跳转>软考全系列 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&…...

代码随想录算法训练营第五十二天| 123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV
今日学习的文章链接和视频链接 123.买卖股票的最佳时机III 视频讲解:https://www.bilibili.com/video/BV1WG411K7AR https://programmercarl.com/0123.%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E7%9A%84%E6%9C%80%E4%BD%B3%E6%97%B6%E6%9C%BAIII.html 188.买卖股票的…...
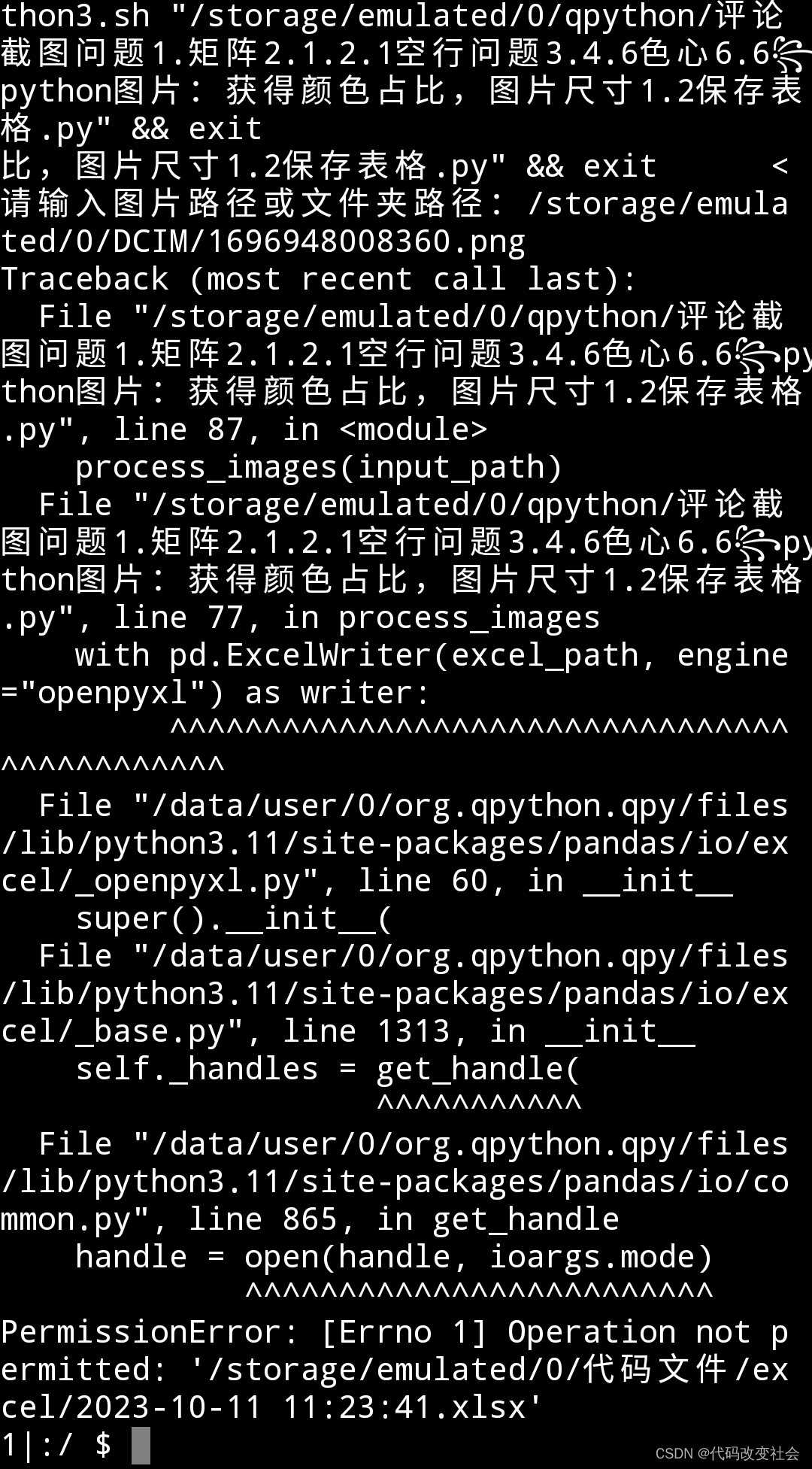
②. GPT错误:图片尺寸写入excel权限错误
꧂问题最初 ꧁ input输入图片路径 print图片尺寸 大小 长宽高 有颜色占比>0.001的按照大小排序将打印信息存储excel表格文件名 表格路径 图片大小 尺寸 颜色类型 占比信息input输入的是文件就处理文件 是文件夹📁就处理文件。路径下的图片 1. 是处理本路径图片 …...

JQuery、JSON、AJAX、XML、IO流、多线程、反射核心知识点详解
JQuery 一、什么是JQuery JQuery是JavaScript的一个框架,对js的封装,使得js简单易学 优点: 1、不用考虑浏览器兼容性问题 2、jquery拥有强大的选择器,简化了js代码 3、jquery提供了很多系统函数,直接调用 二、版本 1.x…...

基于python的多种图像增强算法实现
基于python的多种图像增强算法实现 引言工具算法增强对比度直方图均衡化锐化图像噪声消除中值滤波均值滤波高斯滤波双边滤波增强对比度直方图均衡化总结全部资源引用引言 本项目使用python实现多种空域增强的图像增强算法,并使用了pyqt编写页面。通过点击不同页面的多种按钮,…...
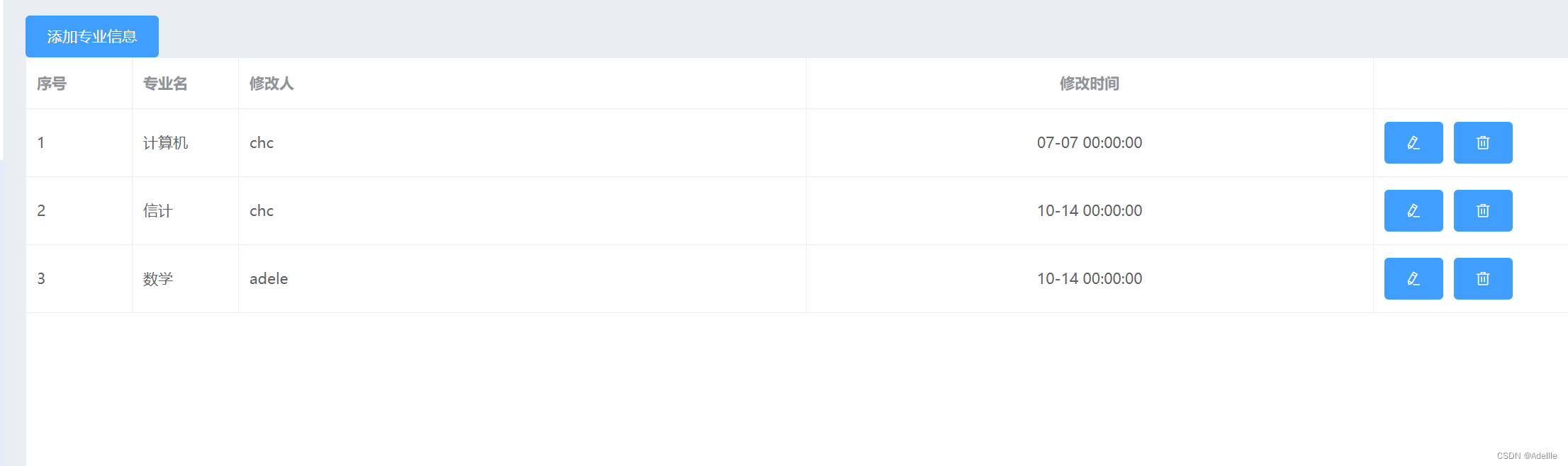
Java前后端交互实现班级管理(查询)
1,数据库创建存储专业信息的表 2,后端: 连接数据库工具类DBUtil.java: package com.ffyc.webserver.util;import java.sql.*;public class DButils {static {try {Class.forName("com.mysql.cj.jdbc.Driver");} catch…...

论文速递 | 8月下旬9月上旬Operations ResearchManagement Science文章精选
编者按 本期我们选取了8月下旬及9月上旬Operations Research文章2篇,Management Science文章4篇期刊文章,着眼于各种不同场景下对于风险的预测、量化及管理,通过聚焦于风险这一主题,体系化地形成文章精选。 文章1 Computation of…...

DataBinding使用报错
val dataBinding DataBindingUtil.setContentView<ActivityMainBinding>(this,R.layout.activity_main)报错一: Unresolved reference: ActivityMainBinding 首先你要知道一个概念,ActivityMainBinding是DataBinding中的一种视频绑定ÿ…...

08Maven中的继承和聚合的作用
Maven中的继承 实际开发中对一个比较大型的项目进行了模块拆分 , 一个project下面创建了很多个modul, 每一个module都需要配置自己的依赖信息 开发中使用的同一个框架内的不同jar包,它们应该是同一个版本,所以整个项目中使用的框架版本需要统一 传统方…...
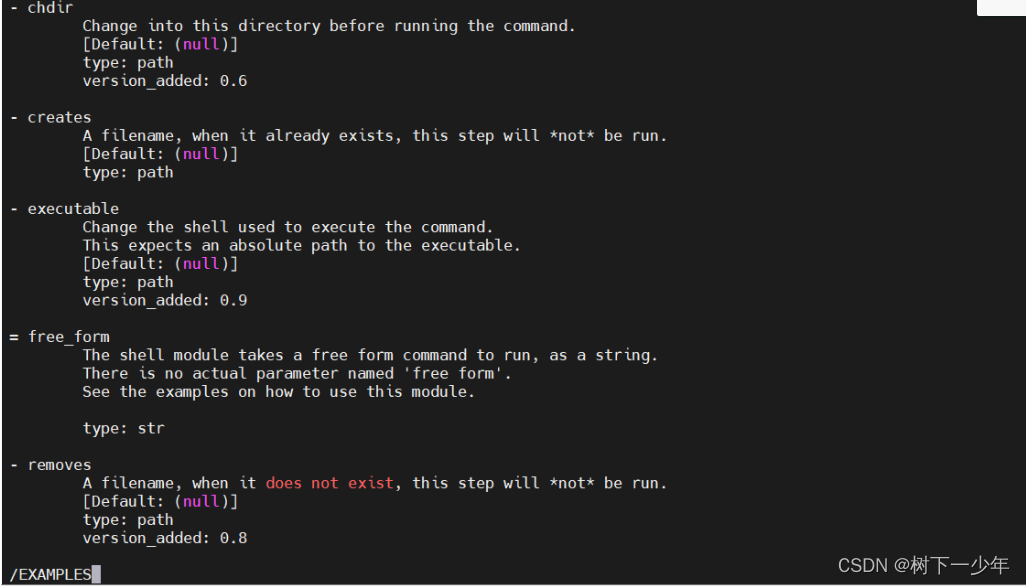
Ansible运行临时命令及常用模块介绍
目录 一.运行临时命令 1.基本语法格式 2.查看当前版本已安装的所有模块 二.ansible常见模块 1.command模块 2.shell模块 3.raw模块 4.script模块 5.file模块 参数列表: 示例: 6.copy模块 参数列表: 示例: 7.fetch模…...
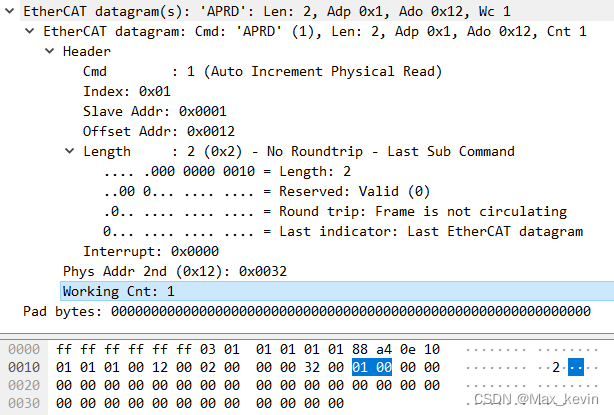
EtherCAT报文-APRD(自动增量读)抓包分析
0.工具准备 1.EtherCAT主站 2.EtherCAT从站(本文使用步进电机驱动器) 3.Wireshark1.EtherCAT报文帧结构 EtherCAT使用标准的IEEE802.3 Ethernet帧结构,帧类型为0x88A4。EtherCAT数据包括2个字节的数据头和44-1498字节的数据。数据区由一个或…...

论文阅读:Seeing in Extra Darkness Using a Deep-Red Flash
论文阅读:Seeing in Extra Darkness Using a Deep-Red Flash 今天介绍的这篇文章是 2021 年 ICCV 的一篇 oral 文章,主要是为了解决极暗光下的成像问题,通过一个深红的闪光灯补光。实现了暗光下很好的成像效果,整篇文章基本没有任…...

将license验证加入到系统中
1.将ClientDemo下的cn文件夹的内容导入项目对应的java目录下。 2.将license-config.properties文件导入resources目录下。 3.在项目的pom.xml中添加如下依赖。 <properties><!-- Apache HttpClient --><httpclient>4.5.5</httpclient><!-- License…...

中断机制-interrupt和isInterrupted源码分析、中断协商案例
当前线程的中断标识为true,是不是线程就立刻停止? 答案是不立刻停止,具体来说,当对一个线程,调用interrupt时: 如果线程处于正常活动状态,那么会将该线程的中断标志设置为true,仅此…...

我与COSCon的故事【时光的故事】
曾经 2019年的时候,我还在日本读研究生,做一些物联网 (Internet of Things, IoT) 网络中的底层P2P (Peer to Peer) 通讯仿真模拟。这个方向是新来的Nguyen老师的新方向,它跟计算机强相关,但是很小众,实验室里也没有前辈…...
)
【科学文献计量】利用pybibx分析Scopus文献数据集(EDA,N-Grams,Cluster,Network analysis,NLP)
利用pybibx分析Scopus文献数据集 1 运行前准备1.1 数据集1.2 前置库2 加载库3 数据导入4 探索式数据分析,即EDA4.1 表格可视化4.2 词云图可视化4.3 N-Grams可视化4.4 文献聚类4.5 主题词演化4.6 桑基图可视化4.7 树图可视化4.8 作者生产力可视化5 网络可视化5.1 文献引用与被引…...
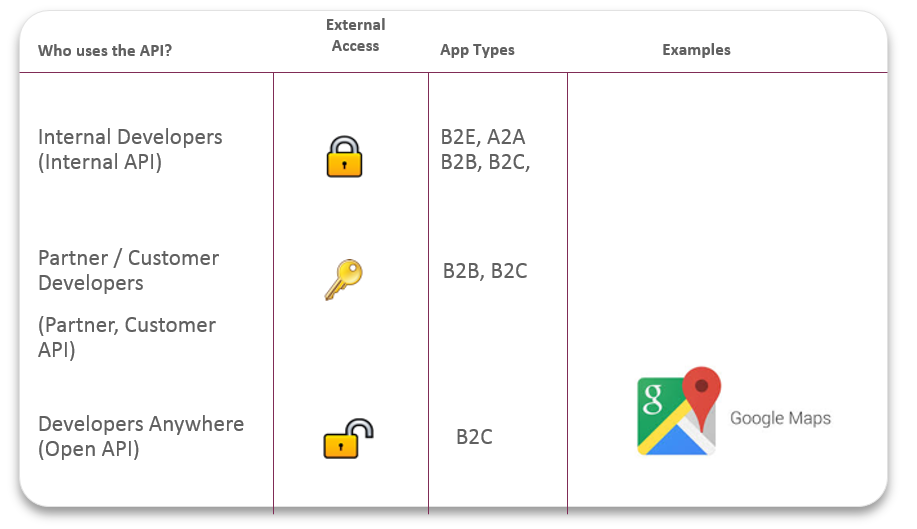
-带你看懂11种API类型及应用-
一起走进多样的API,多样的精彩 随着互联网行业的日益发展,API(Application Programming Interface)这个名词对于绝大多数来说都已不再陌生。然而,实际上,根据不同标准可以划分出不同类型的API。今天,让我们来走…...

集成友盟qq互联分享,导出风险问题处理
处理方案:移除 android:exported"true"即可。 注意友盟SDK QQ share 里默认配置是android:exported"true",所以要覆盖即可。...
探索数字安全的卓越之选 - Digicert证书
在数字时代,数据安全和隐私保护变得尤为重要。无论是个人网站、电子商务平台还是大型企业,保护用户数据和建立信任都是至关重要的任务。在这个领域,Digicert是一个备受推崇的品牌,提供了卓越的数字证书解决方案,以确保…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
