260. 只出现一次的数字 III
给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
示例 1:
输入:nums = [1,2,1,3,2,5] 输出:[3,5] 解释:[5, 3] 也是有效的答案。
示例 2:
输入:nums = [-1,0] 输出:[-1,0]
示例 3:
输入:nums = [0,1] 输出:[1,0]
提示:
2 <= nums.length <= 3 * 104-231 <= nums[i] <= 231 - 1- 除两个只出现一次的整数外,
nums中的其他数字都出现两次
题解:
位运算
将 x 的所有位都取反得到的值。通过与原数 x 进行按位与运算(&),可以得到一个结果,其中只有最低位的 1 保留下来,其他位都为 0。
这个方法的原理在于,当对一个数 x 取反时,得到的 -x 在二进制表示上是 x 的按位取反加 1。因此,-x 的二进制表示中最低位的 1 对应的位置就是 x 中最低位的 1 的位置。通过与 x 进行按位与运算,可以将这个最低位的 1 提取出来。
code:
public int[] singleNumber(int[] nums) {int xorsum = 0;for (int num : nums) {xorsum^= num;}// 防止溢出int lsb = (xorsum == Integer.MIN_VALUE ? xorsum : (xorsum & -xorsum));int type1 = 0, type2 = 0;for (int num : nums) {if ((num & lsb) != 0) {type1 ^= num;} else {type2 ^= num;}}return new int[]{type1, type2};}相关文章:

260. 只出现一次的数字 III
给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。 你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。 示例 1: 输入&…...

家政预约接单系统,家政保洁小程序开发;
家政预约接单系统,家政保洁维修小程序开发,阿姨管理,家政保险,合同管理,资金管理,营销推广等功能,包括:推广、营销、管理、培训、周边服务等等 家政系统详细功能介绍: 家…...

网络安全工程师需要学什么?零基础怎么从入门到精通,看这一篇就够了
网络安全工程师需要学什么?零基础怎么从入门到精通,看这一篇就够了 我发现关于网络安全的学习路线网上有非常多看似高大上却无任何参考意义的回答。大多数的路线都是给了一个大概的框架,告诉你那些东西要考,以及建议了一个学习顺…...
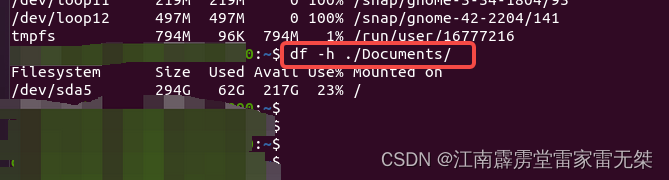
出差学知识No3:ubuntu查询文件大小|文件包大小|磁盘占用情况等
1、查询单个文件占用内存大小2、显示一个目录下所有文件和文件包的大小3、显示ubuntu所有磁盘的占用情况4、查看ubuntu单个包的占用情况 1、查询单个文件占用内存大小 使用指令:ls -lh 文件 2、显示一个目录下所有文件和文件包的大小 指令:du -sh* 3…...

详解cv2.copyMakeBorder函数【OpenCV图像边界填充Python版本】
文章目录 简介函数原型代码示例参考资料 简介 做深度学习图像数据集时,有时候需要调整一张图片的长和宽。如果直接使用cv2.resize函数会造成图像扭曲失真,因此我们可以采取填充图像短边的方法解决这个问题。cv2.copyMakeBorder函数提供了相关操作。本篇…...
前端技术-并发请求
并发请求 代码解释 定义了一个函数 concurRequest,用于并发请求多个 URL 并返回它们的响应结果。 function concurRequest(urls, maxNum) {return new Promise((resolve, reject) > {if (urls.length 0) {resolve([]);return;}const results [];let index …...
:React中获取Refs的几种方式)
面试题-React(十三):React中获取Refs的几种方式
一、Refs的基本概念 Refs是React提供的一种访问DOM元素或组件实例的方式。通过Refs,我们可以在React中获取到底层的DOM节点或组件实例,并进行一些操作。Refs的使用场景包括但不限于:访问DOM属性、调用组件方法、获取输入框的值等。 二、获取…...

Linux CentOS 7升级curl8.4.0使用编译安装方式
1、查看当前版本 # curl --version curl 7.29.0 (x86_64-redhat-linux-gnu) libcurl/7.29.0 NSS/3.19.1 Basic ECC zlib/1.2.7 libidn/1.28 libssh2/1.4.3 Protocols: dict file ftp ftps gopher http https imap imaps ldap ldaps pop3 pop3s rtsp scp sftp smtp smtps tel…...
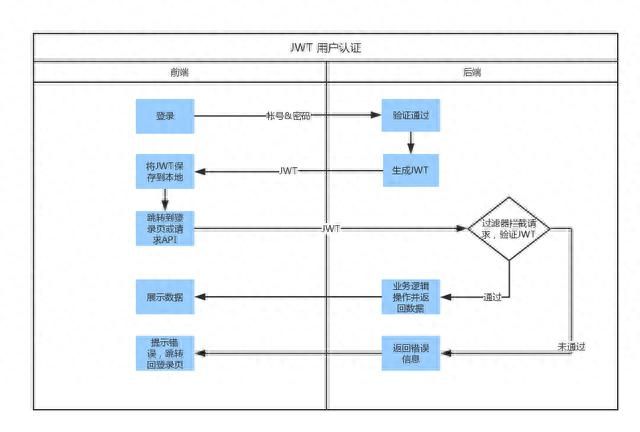
探寻JWT的本质:它是什么?它有什么作用?
JWT(JSON Web Token)是一种基于 JSON 格式的轻量级令牌(token)协议,它被广泛应用于网络应用程序的身份验证和授权。相较于传统的 session-based 认证机制,JWT 具有更好的扩展性和互操作性,同时也…...

关于雅思听力答案限定字数的解释。
1. No more than three words and/or a number:31,可以填3/2/1个单词;1个数字;3/2/1个单词1个数字 2. No more than three words and/or numbers:3n,可以填3/2/1个单词;n个数字;3/2…...

化工python | CSTR连续搅拌反应器系统
绝热连续搅拌釜反应器 (CSTR) 是过程工业中常见的化学系统。 容器中发生单个一级放热且不可逆的反应 A → B,假定容器始终完全混合。 试剂 A 的入口流以恒定的体积速率进入罐。 产物流B以相同的体积速率连续排出,液体密度恒定。 因此,反应液体的体积是恒定的。 在反应器中发…...

交通物流模型 | 基于自监督学习的交通流预测模型
交通物流模型 | 基于自监督学习的交通流预测模型 在智能交通系统中,准确预测不同时间段的城市交通流量是至关重要的。现有的方法存在两个关键的局限性:1、大多数模型集中预测所有区域的交通流量,而没有考虑空间异质性,即不同区域的交通流量分布可能存在偏差;2、现有模型无…...
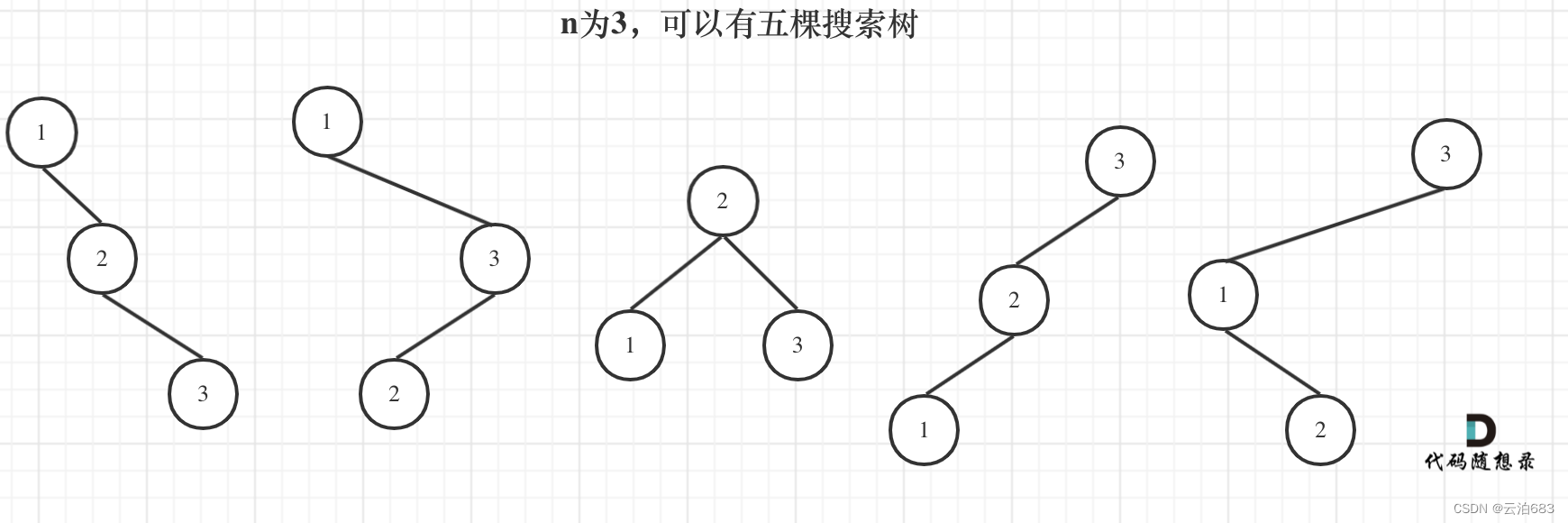
343. 整数拆分 96.不同的二叉搜索树
343. 整数拆分 设dp[i]表示拆分 数字i 出来的正整数相乘值最大的值 (i - j) * j,和dp[i - j] * j是获得dp[i]的两种乘法,在里面求最大值可以得到当前dp[i]的最大值,但是这一次的得出的最大值如果赋值给dp[i],可能没有没赋值的dp[i]大&#…...
)
Vue3理解(9)
侦听器 1.计算属性允许我们声明性地计算衍生值,而在有些情况下,我们需要状态变化时执行一些方法例如修改DOM。 2.侦测数据源类型,watch的第一个参数可以市不同形式的‘数据源’,它可以市一个ref(包括计算属性),一个响应式对象&…...

CRM系统中的销售漏斗有什么作用?
随着数字化发展,越来越多的企业使用CRM销售管理系统提高销售管理水平,提升盈利能力。在这个过程中,销售漏斗起到了非常重要的作用。下面就来说说,CRM系统中的销售漏斗有什么作用? 一、销售数据可视化 CRM销售漏斗通过…...
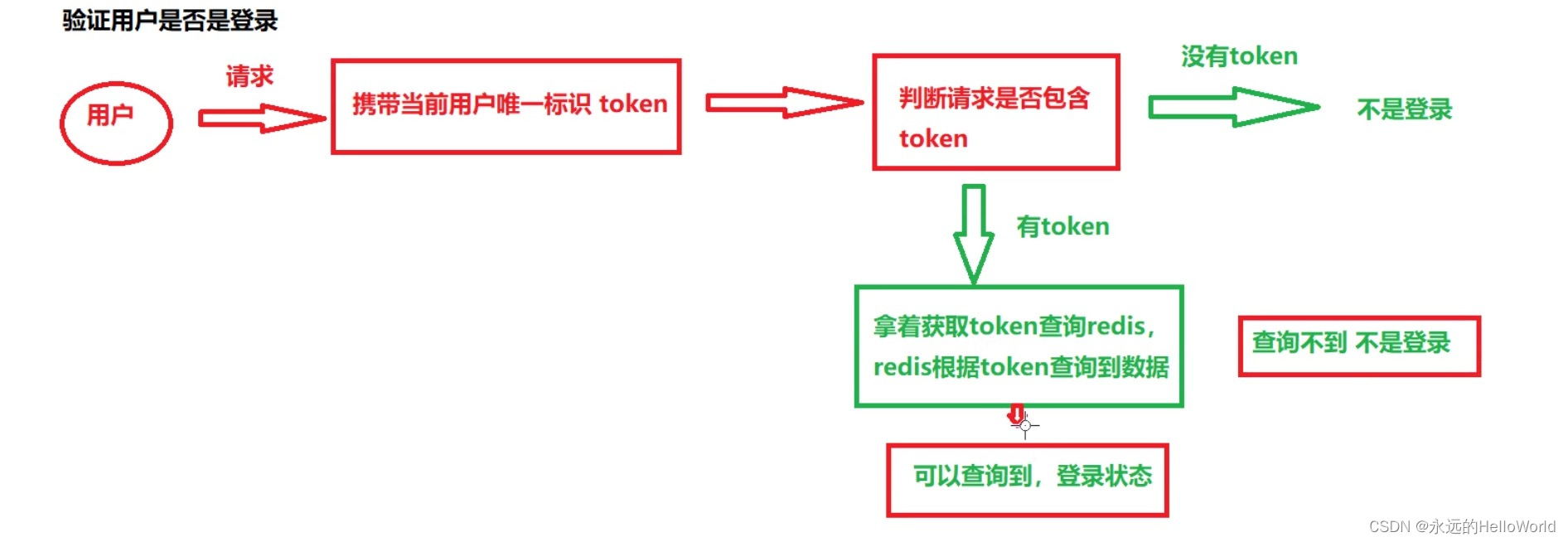
项目(模块1:用户登陆流程分析)
验证登陆点流程...
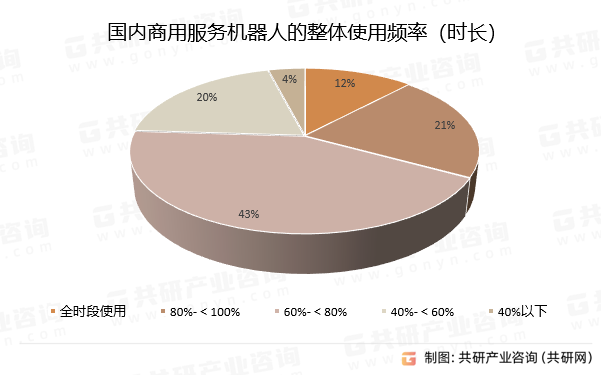
2023年中国商用服务机器人行业发展概况分析:国产机器人厂商向海外进军[图]
商用服务机器人指在非制造业的商用服务场景中,用来替代或辅助人类进行服务性质工作的机器人;常见的商用场景中,商用服务机器人主要分为终端配送类机器人,商用清洁类机器人,引导讲解类机器人等,被广泛应用在…...

千兆光模块和万兆光模块的适用场景有哪些
随着数字化和物联网的普及,对网络速度和带宽的要求也越来越高。千兆光模块和万兆光模块是两种常见的光模块,在不同的应用场景中,它们各具优势。下面我们来探讨一下千兆光模块和万兆光模块的主要适用场景。 首先是企业网络。千兆光模块常用于…...
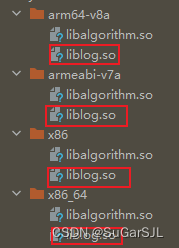
2 files found with path ‘lib/armeabi-v7a/liblog.so‘ from inputs:
下图两个子模块都用CMakeLists.txt引用了android的log库,编译后,在它们的build目录下都有liblog.so的文件。 四个CPU架构的文件夹下都有。 上层模块app不能决定使用哪一个,因此似乎做了合并,路径就是报错里的哪个路径,…...

qt中json类
目录 QJsonValue QJsonObject QJsonArray QJsonDocument 案例: Qt 5.0开始提供了对Json的支持,我们可以直接使用Qt提供的Json类进行数据的组织和解析,下面介绍4个常用的类。 QJsonValue 该类封装了JSON支持的数据类型。 布尔类型…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
