scrollIntoView使用与属性详解
scrollIntoView 使用与属性详解
效果图如下图所示

如果要想让元素滚动到指定位置
window.onload = function () {containerItems[6].scrollIntoView({ behavior: "smooth" });
};
js 代码
const containerItems = document.querySelectorAll(".container div");
const gobackTop = document.querySelector(".gobackTop");window.onload = function () {containerItems[6].scrollIntoView({ behavior: "smooth" });
};gobackTop.addEventListener("click", function () {window.scrollTo(0, 0);
});
html 元素
<div class="container"><div><h1>1</h1></div><div><h1>2</h1></div><div><h1>3</h1></div><div><h1>4</h1></div><div><h1>5</h1></div><div><h1>6</h1></div><div><h1>7</h1></div><div><h1>8</h1></div><div><h1>9</h1></div><div><h1>10</h1></div><div><h1>11</h1></div><div><h1>12</h1></div><div><h1>13</h1></div><div><h1>14</h1></div><div><h1>15</h1></div><div><h1>16</h1></div>
</div><div class="gobackTop">返回顶部</div>
css 样式
html {/* 平滑滚动到顶部 */scroll-behavior: smooth;
}.container {margin: 0 auto;width: 300px;
}.container > div {width: 300px;height: 300px;text-align: center;line-height: 300px;background-color: #efcd11;
}.gobackTop {position: fixed;bottom: 50px;right: 50px;width: 50px;height: 50px;background-color: #efcd11;
}
相关文章:

scrollIntoView使用与属性详解
scrollIntoView 使用与属性详解 效果图如下图所示 如果要想让元素滚动到指定位置 window.onload function () {containerItems[6].scrollIntoView({ behavior: "smooth" }); };js 代码 const containerItems document.querySelectorAll(".container div&…...
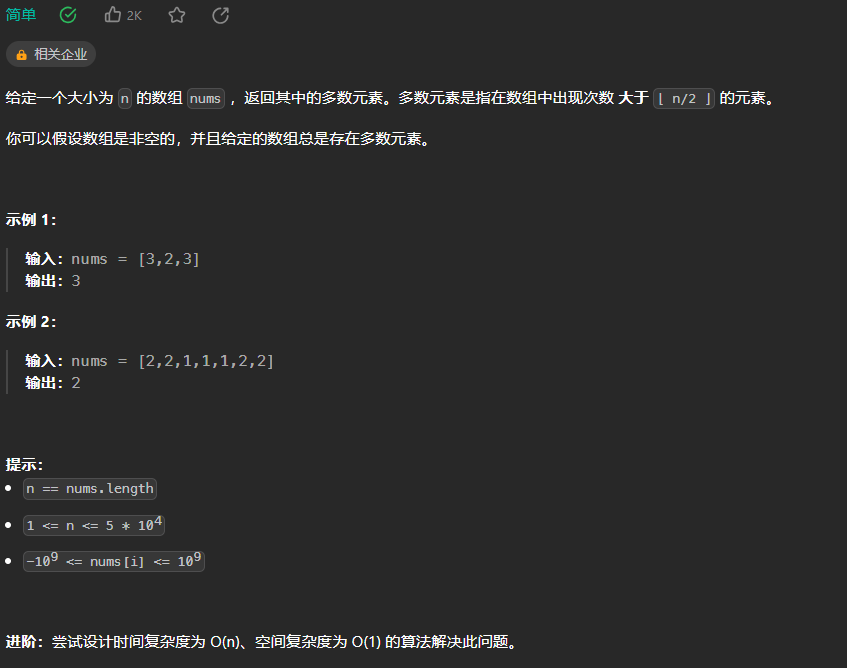
【LeetCode热题100】--169.多数元素
169.多数元素 使用哈希表: class Solution {public int majorityElement(int[] nums) {int n nums.length;int m n/2;Map<Integer,Integer> map new HashMap<>(); //定义一个hashfor(int num:nums){Integer count map.get(num); //Map.get() 方法…...

LeetCode 面试题 10.01. 合并排序的数组
文章目录 一、题目二、C# 题解 一、题目 给定两个排序后的数组 A 和 B,其中 A 的末端有足够的缓冲空间容纳 B。 编写一个方法,将 B 合并入 A 并排序。 初始化 A 和 B 的元素数量分别为 m 和 n。 示例: 输入: A [1,2,3,0,0,0], m 3 B [2,5,6], n 3 输…...

揭秘OLED透明拼接屏的参数规格:分辨率、亮度与透明度全解析
作为一种新型的显示技术,OLED透明拼接屏在市场中正在迅速崭露头角,有很多知名品牌厂家能设计、开发、生产高品质的显示产品。 如尼伽、起鸿、康视界、LG、YCTIMES、腾裕等,这些品牌在显示技术领域拥有丰富的经验和声誉,以其卓越的…...

竞赛选题 深度学习YOLOv5车辆颜色识别检测 - python opencv
文章目录 1 前言2 实现效果3 CNN卷积神经网络4 Yolov56 数据集处理及模型训练5 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习YOLOv5车辆颜色识别检测 ** 该项目较为新颖,适合作为竞赛课题方向࿰…...
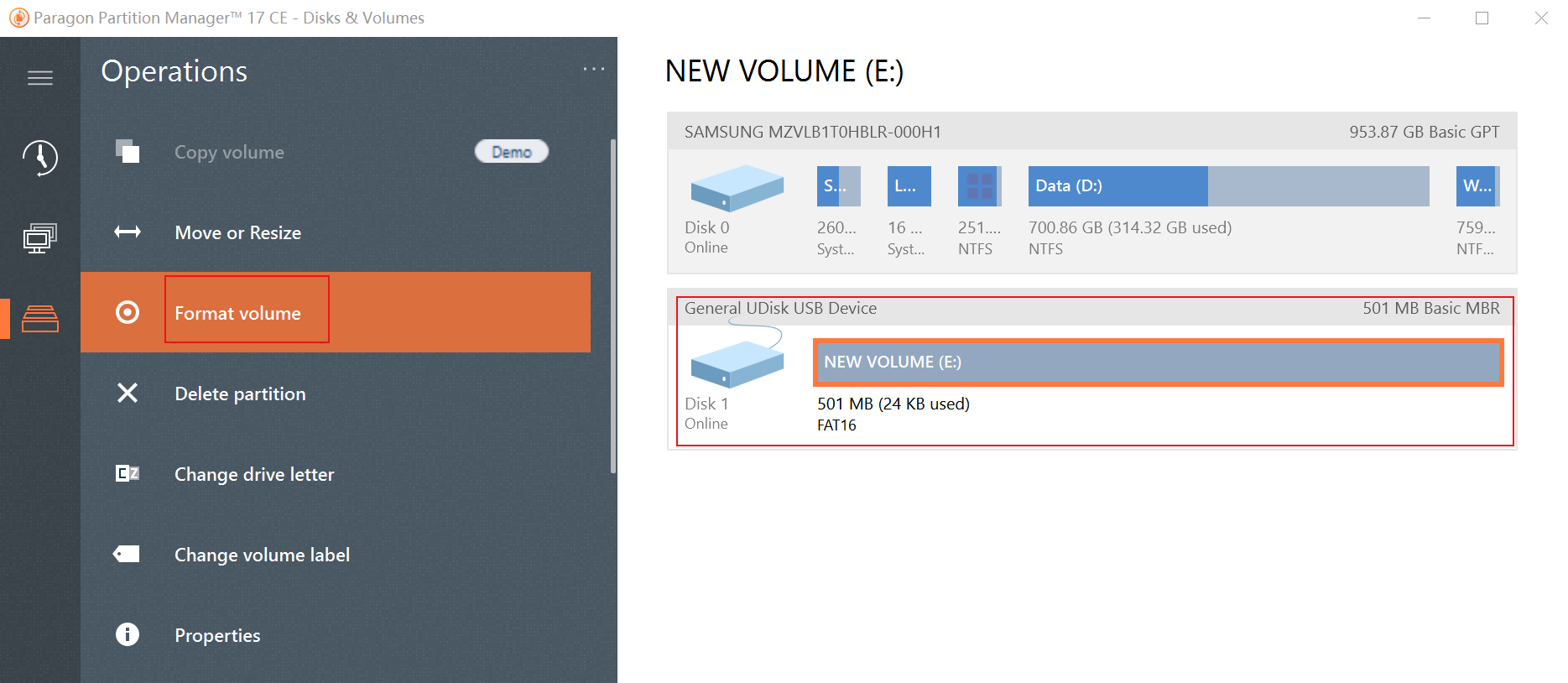
linux U盘无法使用,提示“Partition table entries are not in disk order“
问题: U盘在Windows上使用正常,在linux下无法使用fdisk -l 命令提示:Partition table entries are not in disk order $ fdisk -l Disk /dev/sdb: 525 MB, 525336576 bytes 17 heads, 59 sectors/track, 1022 cylinders Units cyl…...

HDLbits: Fsm ps2
本题目理解起来有点难,要观察题目中给的三个时序图,通过时序图可以发现,状态有四个:byte1、byte2、byte3,还有一个“?”状态。其中,byte1的下一个状态一定是byte2,byte2的下一个状态…...
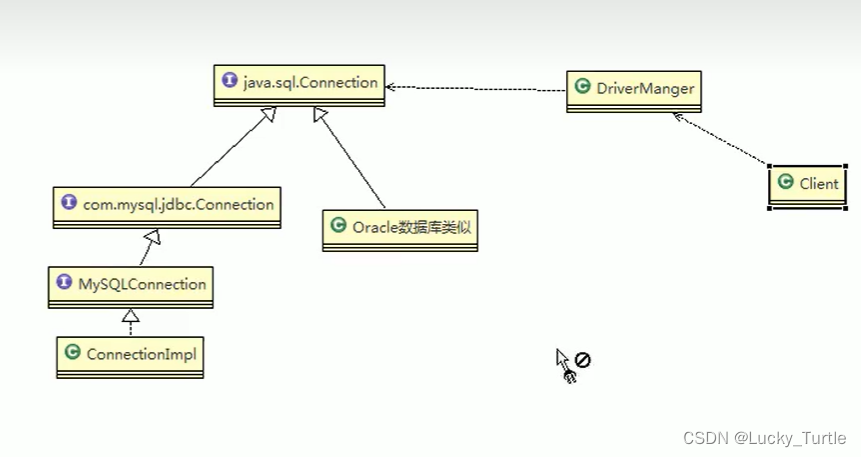
【设计模式】八、桥接模式
文章目录 举例问题分析基本介绍桥接模式在 JDBC 的源码剖析桥接模式的注意事项和细节JDBC 举例 现在对不同手机类型的不同品牌实现操作编程(比如:开机、关机、上网,打电话等), 传统方法对应的类图: 问题分析 扩展性问题(类爆炸)ÿ…...

从零开始的stable diffusion
stable diffusion真的是横空出世,开启了AIGC的元年。不知你是否有和我一样的困惑,这AI工具好像并不是那么听话? 前言 我们该如何才能用好stable diffusion这个工具呢?AI究竟在stable diffusion中承担了什么样的角色?如…...

【Qt之QString】数值与进制字符串间的转换详解
在Qt中,可以使用QString类提供的一些方法来进行数值和进制字符串之间的转换。 以下是示例: 1. 将整数转换为进制字符串: QString类的number静态方法用于将整数转换为字符串表示,并且可以指定转换的进制。方法的定义如下&#x…...

Pytest单元测试框架 —— Pytest+Allure+Jenkins的应用
一、简介 pytestallurejenkins进行接口测试、生成测试报告、结合jenkins进行集成。 pytest是python的一种单元测试框架,与python自带的unittest测试框架类似,但是比unittest框架使用起来更简洁,效率更高 allure-pytest是python的一个第三方…...

科普向丨语音芯片烧录工艺的要求
语音芯片烧录工艺要求烧录精度、速度、内存容量、电源稳定性、兼容性和数据安全性。这些要素需优化和控制以保证生产高效、稳定、安全并烧录出高质量的语音芯片。不同厂家生产的语音芯片在烧录工艺上存在差异,需相应设计和研发以实现兼容。 一、烧录精度 语音芯片烧…...
 但是它将不会被安装 或)
: 依赖: qtbase5-dev (= 5.12.8+dfsg-0ubuntu2.1) 但是它将不会被安装 或
有一些软件包无法被安装。如果您用的是 unstable 发行版,这也许是因为系统无法达到您要求的状态造成的。E: 无法修正错误,因为您要求某些软件包保持现状,就是它们破坏了软件包间的依赖关系。_unstable发行版-CSDN博客 E: 无法修正错误&#x…...

Unity中Camera类实现坐标系转换的示例
1. 用于将世界坐标系转换为屏幕坐标系 using System.Collections; using System.Collections.Generic; using UnityEngine;public class Camer_Class_WorldTo : MonoBehaviour {// 用于将世界坐标系转换为屏幕坐标系//本脚本将完成一个案例实现 小球从远处过来Transform Sta…...

vue-按键修饰符
按键修饰符:主要用于监听键盘上的按钮被按下时,可触发对应的事件函数 v-on:keyup.修饰符.修饰符】、 .enter .tab .delete(针对delete和backspace两个按键) .esc .space .esc .space .up .down .left .right 系统修饰符必须按下才触发 .ctrl .alt .shift…...
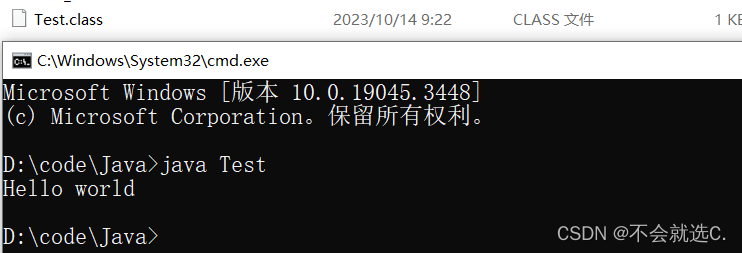
[初始java]——java为什么这么火,java如何实现跨平台、什么是JDK/JRE/JVM
java的名言: ”一次编译、到处运行“ 一、编译语言与解释语言 编译: 是将整份源代码转换成机器码再进行下面的操作,最终形成可执行文件 解释: 是将源代码逐行转换成机器码并直接执行的过程,不需要生成目标文件 jav…...

R语言手动绘制NHANSE数据基线表并聊聊NHANSE数据制作亚组交互效应表的问题(P for interaction)
美国国家健康与营养调查( NHANES, National Health and Nutrition Examination Survey)是一项基于人群的横断面调查,旨在收集有关美国家庭人口健康和营养的信息。 地址为:https://wwwn.cdc.gov/nchs/nhanes/Default.aspx 在既往的…...
)
C++引用(起别名)
0.引用的概念 引用不是新定义一个变量,而是给已存在变量取了一个别名,从语法的角度来说编译器不会为引用变量开辟内存空间,它和它引用的变量共用同一块内存空间。比如说你的名字和外号指的都是你本人。 void Test() {int a 10;int& ra …...
Ubuntu:VS Code IDE安装ESP-IDF【保姆级】(草稿)
物联网开发学习笔记——目录索引 Visual Studio Code(简称“VS Code”)是Microsoft向开发者们提供的一款真正的跨平台编辑器。 参考: VS Code官网:Visual Studio Code - Code Editing. Redefined 乐鑫官网:ESP-IDF …...
rust解法)
子序列(All in All, UVa 10340)rust解法
输入两个字符串s和t,判断是否可以从t中删除0个或多个字符(其他字符顺序不变),得到字符串s。例如,abcde可以得到bce,但无法得到dc。 解法 use std::io;fn main(){let mut buf String::new();io::stdin().…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
