洛谷P1123 取数游戏(C++)(DFS)
目录
1.题目
题目描述
输入格式
输出格式
输入输出样例
说明/提示
2.AC
1.题目
题目描述
一个N \times MN×M的由非负整数构成的数字矩阵,你需要在其中取出若干个数字,使得取出的任意两个数字不相邻(若一个数字在另外一个数字相邻88个格子中的一个即认为这两个数字相邻),求取出数字和最大是多少。
输入格式
第1行有一个正整数TT,表示了有TT组数据。
对于每一组数据,第一行有两个正整数NN和MM,表示了数字矩阵为NN行MM列。
接下来NN行,每行MM个非负整数,描述了这个数字矩阵。
输出格式
TT行,每行一个非负整数,输出所求得的答案。
输入输出样例
输入 #13
4 4
67 75 63 10
29 29 92 14
21 68 71 56
8 67 91 25
2 3
87 70 85
10 3 17
3 3
1 1 1
1 99 1
1 1 1输出 #1271
172
99说明/提示
对于第1组数据,取数方式如下:
[67] 75 63 10
29 29 [92] 14
[21] 68 71 56
8 67 [91] 25
对于20\%20%的数据,N, M≤3N,M≤3;
对于40\%40%的数据,N,M≤4N,M≤4;
对于60\%60%的数据,N, M≤5N,M≤5;
对于100\%100%的数据,N, M≤6,T≤20N,M≤6,T≤20。
2.AC
#include <iostream>
#include <string.h>
using namespace std;int n, m, ans;
int a[10][10], v[10][10];
int tx[8] = {0,1,1,1,0,-1,-1,-1}, ty[8] = {1,1,0,-1,-1,-1,0,1};int f1(int cx,int cy) {v[cx][cy]++;for (int i = 0; i < 8; i++) {int x = cx + tx[i];int y = cy + ty[i];if (x < 0 || y < 0 || x >= n || y >= m) continue;v[x][y]++;}
}int f2(int cx,int cy) {v[cx][cy]--;for (int i = 0; i < 8; i++) {int x = cx + tx[i];int y = cy + ty[i];if (x < 0 || y < 0 || x >= n || y >= m) continue;v[x][y]--;}
}int dfs (int cx, int cy, int sum) {if (cy == m) {cx++;cy = 0;}if (cx == n) {ans = max(ans,sum);return 0;}dfs(cx,cy+1,sum);if (!v[cx][cy]) {f1(cx,cy);dfs(cx,cy+1,sum+a[cx][cy]);f2(cx,cy);}return 0;
}int main()
{int T;cin>>T;while (T--) {ans = 0;memset(v,0,sizeof(v));cin>>n>>m;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {cin>>a[i][j];} }dfs(0,0,0);cout<<ans<<endl;}return 0;
}相关文章:
(DFS))
洛谷P1123 取数游戏(C++)(DFS)
目录 1.题目 题目描述 输入格式 输出格式 输入输出样例 说明/提示 2.AC 1.题目 题目描述 一个N \times MNM的由非负整数构成的数字矩阵,你需要在其中取出若干个数字,使得取出的任意两个数字不相邻(若一个数字在另外一个数字相邻88个格…...

Python Qt6快速入门-嵌入PyQtGraph图表
嵌入PyQtGraph 文章目录 嵌入PyQtGraph1、PyQtGraph介绍2、创建PyQtGraph小部件3、绘图样式配置3.1 背景颜色3.2 线条颜色、线宽和样式配置3.3 线标记(Line Markers)3.4 绘制标题3.5 轴标题3.6 图例(Legends)3.7 轴范围限制3.8 绘制多组数据3.10 画布清空4、更新数据5、总结1、…...
Mac电脑_GitHub提交项目至仓库
第一步(准备工作): Mac 电脑自带 git , 无需安装 1. 创建一个项目 demo1 在 github 上 2. 创建 ssh 密钥 打开终端: ssh-keygen -t rsa -C "your_emailyouremail.com" 此处输入两次密码, 直接…...

Android自定义View实现横向的双水波纹进度条
效果图:网上垂直的水波纹进度条很多,但横向的很少,将垂直的水波纹改为水平的还遇到了些麻烦,现在完善后发布出来,希望遇到的人少躺点坑。思路分析整体效果可分为三个,绘制圆角背景和圆角矩形,绘…...
Python 之 Pandas 分组操作详解和缺失数据处理
文章目录一、groupby 分组操作详解1. Groupby 的基本原理2. agg 聚合操作3. transform 转换值4. apply二、pandas 缺失数据处理1. 缺失值类型1.1 np.nan1.2 None1.3 NA 标量2. 缺失值处理2.1 查看缺失值的情形2.2 缺失值的判断2.3 删除缺失值2.4 缺失值填充在开始之前ÿ…...

【人工智能 AI】什么是人工智能? What is Artificial Intelligence
目录 Introduction to Artificial Intelligence人工智能概论 What is Artificial Intelligence? 什么是人工智能?...

17、触发器
文章目录1 触发器概述2 触发器的创建2.1 创建触发器语法2.2 代码举例3 查看、删除触发器3.1 查看触发器3.2 删除触发器4 触发器的优缺点4.1 优点4.2 缺点4.3 注意点尚硅谷MySQL数据库教程-讲师:宋红康 我们缺乏的不是知识,而是学而不厌的态度 在实际开发…...

内核并发消杀器(KCSAN)技术分析
一、KCSAN介绍KCSAN(Kernel Concurrency Sanitizer)是一种动态竞态检测器,它依赖于编译时插装,并使用基于观察点的采样方法来检测竞态,其主要目的是检测数据竞争。KCSAN是一种检测LKMM(Linux内核内存一致性模型)定义的数据竞争(data race)的工…...

蓄水池抽样算法
蓄水池抽样,也称水塘抽样,是随机抽样算法的一种。基本抽样问题有一批数据(假设为一个数组,可以逐个读取),要从中随机抽取一个数字,求抽得的数字下标。常规的抽样方法是,先读取所有的…...

数据结构预算法之买股票最好时机动态规划(可买卖多次)
一.题目二.思路在动规五部曲中,这个区别主要是体现在递推公式上,其他都和上一篇文章思路是一样的。所以我们重点讲一讲递推公式。这里重申一下dp数组的含义:dp[i][0] 表示第i天持有股票所得现金。dp[i][1] 表示第i天不持有股票所得最多现金如…...
)
华为OD机试真题Java实现【蛇形矩阵】真题+解题思路+代码(20222023)
蛇形矩阵 蛇形矩阵是由1开始的自然数依次排列成的一个矩阵上三角形。 例如,当输入5时,应该输出的三角形为: 1 3 6 10 15 2 5 9 14 4 8 13 7 12 11请注意本题含有多组样例输入。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Java)真题目录汇总 输入描述:…...
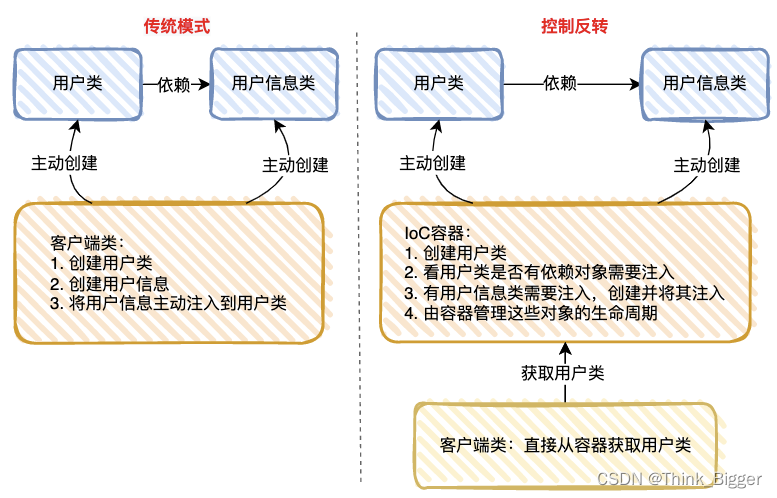
spring Bean的生命周期 IOC
文章目录 1. 基础知识1.1 什么是 IoC ?2. 扩展方法3. 源码入口1. 基础知识 1.1 什么是 IoC ? IoC,控制反转,想必大家都知道,所谓的控制反转,就是把 new 对象的权利交给容器,所有的对象都被容器控制,这就叫所谓的控制反转。 IoC 很好地体现了面向对象设计法则之一 —…...

详解cors跨域
文章目录同源策略cors基本概念cors跨域方式简单请求 simple request非简单请求- 预检请求CORS兼容情况CORS总结同源策略 在以前的一篇博客中有介绍,同源策略是一种安全机制,为了预防某些恶意的行为,限制浏览器从不同源文档和脚本进行交互的行…...
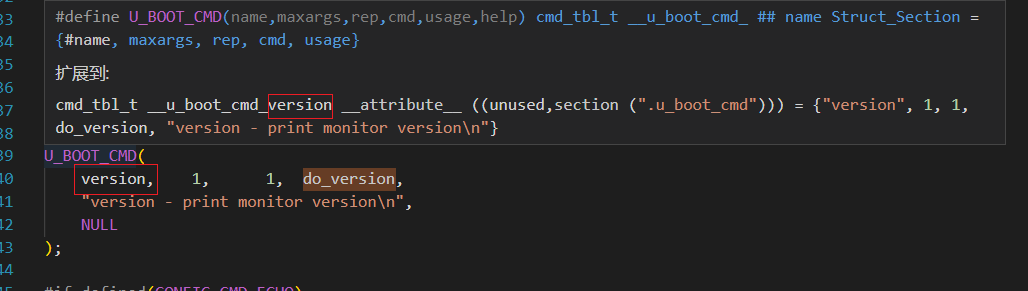
ARM uboot 源码分析7 - uboot的命令体系
一、uboot 命令体系基础 1、使用 uboot 命令 (1) uboot 启动后进入命令行环境下,在此输入命令按回车结束,uboot 会收取这个命令然后解析,然后执行。 2、uboot 命令体系实现代码在哪里 (1) uboot 命令体系的实现代码在 uboot/common/cmd_xx…...

物理服务器与云服务器备份相同吗?
自从云计算兴起以来,服务器备份已经从两阶段的模拟操作演变为由云服务器备份软件执行的复杂的多个过程。但是支持物理服务器和虚拟服务器之间的备份相同吗?主要区别是什么?我们接下来将详细讨论这个问题。 物理服务器与云服务器备份的区别 如果您不熟悉虚拟服务器…...

【Linux】system V共享内存 | 消息队列 | 信号量
🌠 作者:阿亮joy. 🎆专栏:《学会Linux》 🎇 座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉system V共…...

FSC的宣传许可 答疑
【FSC的宣传许可 答疑】问:已经采购了认证产品但没有贴FSC标签,是否可以申请宣传许可?答:不可以。要宣传您采用了FSC认证产品的前提条件之一是产品必须是认证且贴有标签的。如果产品没有贴标,则不可申请宣传许可。您的…...

Leetcode力扣秋招刷题路-0100
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结 100. 相同的树 给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是…...

协作对象死锁及其解决方案
协作对象死锁及其解决方案 1.前言 在遇到转账等的需要保证线程安全的情况时,我们通常会使用加锁的方式来保证线程安全,但如果无法合理的使用锁,很可能导致死锁。或者有时我们使用线程池来进行资源的使用,如调用数据库࿰…...

良许也成为砖家啦~
大家好,我是良许。 没错,良许成为砖家啦,绝不是口嗨,有图有真相! 有人会说,咦,这明明是严宇啊,跟你良许有啥关系? 额。。老读者应该知道良许的来历—— 鄙人真名严宇&a…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...
