算法通过村第十四关-堆|白银笔记|经典问题
文章目录
- 前言
- 在数组中寻找第K大的元素
- 堆排序原理
- 合并K个排序链表
- 总结
前言
提示:想要从讨厌的地方飞出来,就得有藏起来的翅膀。 --三岛由纪夫《萨德侯爵夫人》
这里我们主要看一下经典的题目,这三个题目来说都是堆的热点问题。重点再理解处理方式就行。
在数组中寻找第K大的元素
参考题目地址:215. 数组中的第K个最大元素 - 力扣(LeetCode)


这个题目的道理非常简单,主要的方法有三种:
- 选择法
- 堆查找法
- 快速排序法
选择法很简单,就是遍历一边找到最大的元素,然后再遍历一遍找第二大的,然后再遍历一遍找第三大…直到第K次,就可以找到目标值。但是这种方法只适合面试的时候预热,面试官不会让你写这么简单的代码,因为这个方法的时间复杂度为O(NK)。
比较好的方法就是堆排序和快速排序。快速排序我们已经分析过了,这里看看堆排序的,看看怎么解决。
快排推荐⭐⭐⭐⭐:算法通过村第十关-快排|青铜笔记|快排也没那么难-CSDN博客
其实这个题目采用大顶堆和小顶堆都是可以解决的,但是我们这里推荐**“找最大用最小,找最小用最大”**,找中间用两个堆呗,这样更容易理解,适用的范围也更广。我们构造一个大小只有4的小顶堆,为了更好说明问题,我们扩展以下序列:【3,2,3,1,2,4,5,1,5,6,2,3】。
堆满了之后,对于小顶堆,并一定所有新来的元素都可以入堆的,只有大于根元素的才可以插入到堆中,否则就直接抛弃掉。这是一个重要的前提。
另外元素进入的时候,先替换根元素,如果发现左右两个子树都小该怎么办呢?很显然应该是更小的那个比较,这样才能保证根元素一定是当前堆最小的。假如两个子孩的值一样呢?那就随便选一个。
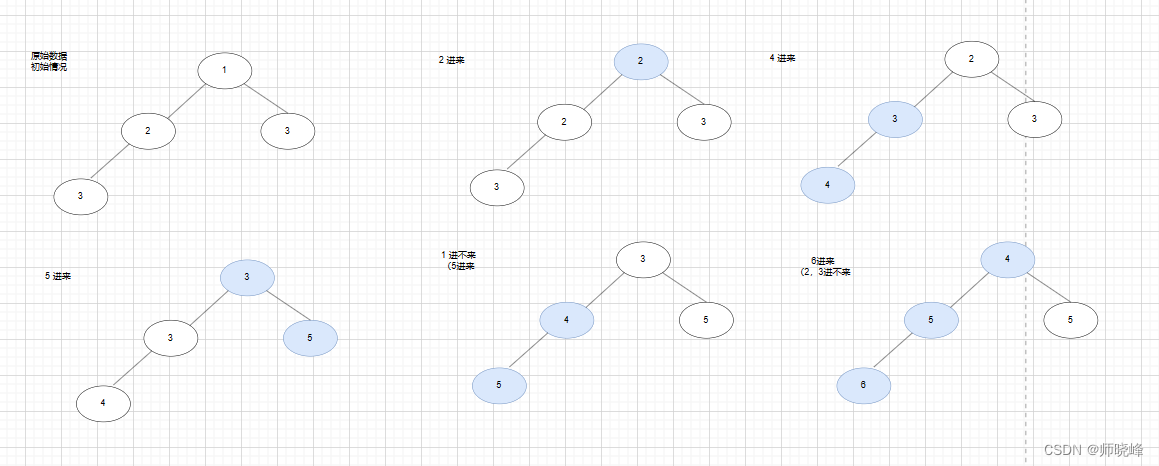
新元素插入的时候只是替换根元素,然后重新构造小顶堆,完成之后,你会神奇的发现此时根的元素正好是第四大的元素。
这时候你会发现,不管要处理多大的序列,或者是不是固定的,根元素每次都是恰好是当前序列下的第K大的元素。上面图的篇幅优先,注意省略了一部分调成的环节,这里好好看看。
上面的代码自己实现起来非常困难,我们可以借助JDK的优先队列来解决,其思路是很简单的。由于第K大的元素,其实就是整个数组排序以后后面半部分最小的那个元素,这里就可以注意,我们可以维护一个有K个元素的最小堆:
- 如果当前堆不满,直接添加
- 堆满的时候,如果新读到的数小于等于堆顶,肯定不是我们要找的元素,只有新遍历到的数大于堆顶的时候,才能将堆顶拿出,然后放入新读到的数,进而让堆自己去调整内部的结构。
说明:这里最适合的操作其实是replace(),即直接把新读到的元素放入堆顶,然后执行下沉(siftDown())操作。Java中PriorityQueue没有提供这个操作,只好先poll再offer
优先队列的写法有很多,这里只例举一个有代表性,其他的写法都差不多,没有本质区别。
看代码如下:
/*** 数组中的第K个最大元素* @param nums* @param k* @return*/public static int findKthLargest(int[] nums, int k) {// 当然k不合理,就直接结束if (k > nums.length) {return -1;}// 获取数组长度int n = nums.length;// 创建包含k个元素的小顶堆PriorityQueue<Integer> minHeap = new PriorityQueue<>(k, (a, b) -> a - b);for (int i = 0; i < k; i++) {minHeap.add(nums[i]);}for (int i = k; i < n; i++) {// 获取堆顶元素 比较是否需要替换Integer topEle = minHeap.peek();// 这里只有大于 才能进if (nums[i] > topEle) {minHeap.poll();minHeap.offer(nums[i]);}}return minHeap.peek();}
堆查找与一般的查找一个显著的优势点是可以对于超大数量的数据进行查找,还能堆数量位置的流数据进行查找。推荐一个题目⭐⭐⭐⭐:
703. 数据流中的第 K 大元素 - 力扣(LeetCode)
这里重要的是记住:找第k大用小顶堆,找第K小用大顶堆。
具体来说:
k多大就建立多大的固定堆
找最大用小顶堆
只和根元素比较,满足条件在能进去
堆排序原理
查找:找小用大,找大用小
排序:升序用小,降序用大
前面介绍了如何使用堆来进行特殊情况的查找,堆的另一个很重要的作用就是排序,那么要怎么排序呢?其实非常简单,我们直到再大顶堆中,根节点是整个结构最大的元素,我们将其拿走,剩下的元素将会重排,此时根节点的第二大的元素,我们再拿走,依次类推。最后堆只剩一个元素的时候,是不是拿走的数据也就排好了?
具体来说,建堆结束之后,数组中的数据已经按照大顶堆的特性来组织了,数组中的第一个元素就是堆顶,也就是最大元素,我们只要他和最后一个元素交换,那个最大元素就放到下标为n的位置上了。
这个过程上面有点类型“删除堆顶元素”的操作,当堆顶元素移除之后,我们把剩下标为n的元素放到堆顶,然后再通过堆的结构化调整,将剩下的n - 1个元素重新构建成堆,堆调整之后,我们再去取元素,这样一直循环,直至重复下去,直到堆最后剩下一个元素,也就是排序完成了。
当然再上面的过程用,放到最后一个位置的元素就不参与排序和计算了。
看一个例子,我们对一个序列进行排序[2,21,4,53,64,78,90,102],先构造大顶堆,然后然根元素出堆,继续调整大顶堆:
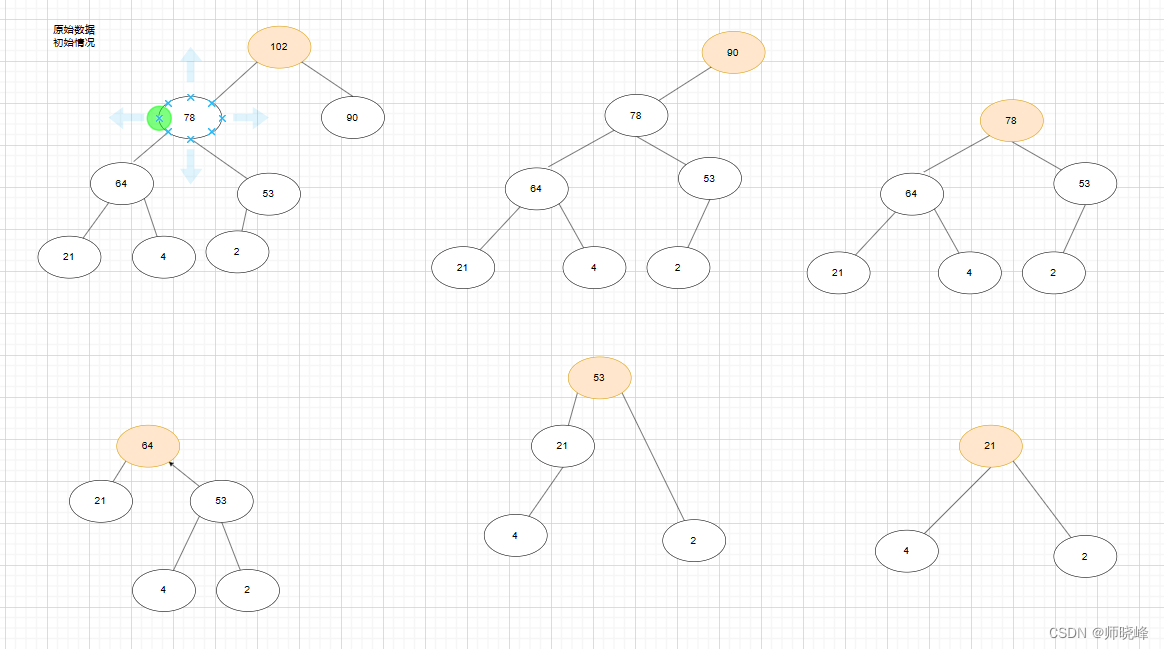
这时候你会发现出堆的序列刚好是:102,90,78,64,53…。也就是从大到小排列。
所以这里可以明白了,如果是小顶堆的化,自然是升序的。所以再排序的时候:
升序用小,降序用大。
记住这个对解题很有用。
合并K个排序链表
参考题目介绍:23. 合并 K 个升序链表 - 力扣(LeetCode)



这个问题的解法五花八门,我们看下用堆排序要怎么处理,因为每个队列都是从小到大排序的,我们每次需要拿到最小值,也就是说我们需要使用小顶堆,构建党法和操作与大顶堆完全一样,不同的是每次比较谁更小。使用堆和并的策略是不过几个链表,最终都是按照顺序来的。每次都是剩余节点的最小值加到输出链表的尾部,然后进行堆的调整,最后合并就完成了。
还有一个问题,这个堆应该有多大呢,给了对少个链表,堆就定义多大。
/*** 合并 K 个升序链表** @param lists* @return*/public ListNode mergeKLists(ListNode[] lists) {if (lists.length == 0 || lists == null) {return null;}// 创建堆PriorityQueue<ListNode> q = new PriorityQueue<ListNode>(Comparator.comparing(node -> node.val));for (int i = 0; i < lists.length; i++) {if (lists[i] != null) {q.add(lists[i]);}}// 虚拟节点ListNode dummy = new ListNode(0);ListNode tail = dummy;while (!q.isEmpty()) {tail.next = q.poll(); // 取最小tail = tail.next; // 链接下一个if (tail.next != null) { // 判断是否到底q.add(tail.next); // 重复下一个}}return dummy.next;}
总结
提示:堆经典问题;大顶堆和小顶堆;手绘原理;堆排序解析;堆查询特点
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题。

相关文章:

算法通过村第十四关-堆|白银笔记|经典问题
文章目录 前言在数组中寻找第K大的元素堆排序原理合并K个排序链表总结 前言 提示:想要从讨厌的地方飞出来,就得有藏起来的翅膀。 --三岛由纪夫《萨德侯爵夫人》 这里我们主要看一下经典的题目,这三个题目来说都是堆的热点问题。重点再理解处理…...

如何正确维护实验室超声波清洗器?
实验室一直被视为一个严谨而严肃的场所,实验应遵循一定的步骤,使用的设备也经历了详细的选择,如实验室超声波清洗机,其特点远强于一般类型的清洗机。专门负责采购的实验室人员一般对优质服务的实验室超声波清洗机印象深刻…...
DID赛道前列的生物识别技术,开启Web3时代的大门—MXT
互联网发展的十字路口 互联网从上世纪90年代初发展至今,历经30年,她改变了整个人类的生活方式、沟通形式以及社会发展模式,她的影响早已渗透到了世界的各个角落。而如今,我们似乎正站在一个新的十字路口,一个互联网将…...

Java基础面试-final
final(最终的) 修饰类:表示类不可被继承修饰方法:表示方法不可被子类覆盖,但是可以重载修饰变量:表示变量一旦被赋值就不可以更改它的值 修饰成员变量 如果final修饰的是类变量,只能在静态初始…...

全波形反演的目标和技术
本篇文章主要讲述了全波形反演的目标和可能用到的方法,对其概念进行解释,以加深理解。若有不正确的地方,欢迎批评指正。 一. 全波形反演的目标: 1. 如何保障模型的拟合能力? 2. 如何保障模型的泛化能力? 3. 如何使结果 (速度模型) 满足物理…...

【SA8295P 源码分析】105 - QNX MISC分区读写、切换A/B启动槽、读取开机次数命令 swdl_utils 介绍 及 祼分区读写 代码实现
【SA8295P 源码分析】105 - QNX MISC分区读写、切换A/B启动槽、读取开机次数命令 swdl_utils 介绍 及 祼分区读写 代码实现 一、切换 A/B 槽启动分区二、读取开机次数三、写 MISC 信息四、Dump Misc 信息五、misc 祼分区读写 代码实现系列文章汇总见:《【SA8295P 源码分析】00…...

Grade 5 Math
数形结合 5 2 3 https://download.csdn.net/download/spencer_tseng/88431286...
)
简易的慢SQL自定义告警实战经验(支持多数据源)
背景 对于慢SQL相信大家都不陌生了,一旦遇到后,相信大家会很快的提供出来对应的优化方法、索引优化建议工具使用等等,对于此我相信大家已经熟悉的不能再熟悉了,但是比较不尽人意的是:在此之前我们往往是花费了大量时间才发现造成系统出现问题的是慢SQL引起的,风险自然而…...

【Springboot】Filter 过滤器的使用
一、基本介绍 过滤器 Filter 作为 Java 三大器之一,在 Java Web 的使用中有很高的地位。所谓过滤器,就是实现了 javax.servlet.Filter 接口的服务器端程序,就是对事物进行过滤的。在 Web 中的过滤器,当然就是对请求进行过滤&#…...

力扣-461.汉明距离
Method 1 直接比较x,y二进制中的每一位,如果不同则cnt加一,并且x,y每次右移一位 class Solution { public:int hammingDistance(int x, int y) {int cnt 0;while(x > 0 && y > 0) {if((x & 1) ! (y & 1)…...
GEE 18:基于GEE平台的土地荒漠化监测与分析【论文复现】
Desertification 1. 研究背景1.1 参考论文1.2 参数获取1.2.1 NDVI1.2.2 Albedo1.2.3 Normalizing indices1.2.4 Calculating the quantitative relationship1.2.5 Calculating DDI2. GEE2.1 数据2.2 GEE code2.2.1 Study region2.2.2 Reomove cloud for Landsat-82.2.3 Calcula…...
平台系统老板驾驶舱的重要性,我选云表
平台系统老板驾驶舱的重要性在于它是一个集成的管理和分析工具,能够提供对平台系统运行情况的全面和实时的监控、分析和管理功能。以下是平台系统老板驾驶舱的重要性: 老板驾驶舱 该表单可供老板实时把控企业运营情况,包括销售业绩、…...

【SpringMVC篇】探索请求映射路径,Get请求与Post请求
🎊专栏【SpringMVC】 🍔喜欢的诗句:天行健,君子以自强不息。 🎆音乐分享【如愿】 🎄欢迎并且感谢大家指出小吉的问题🥰 文章目录 🌺请求映射路径⭐报错原因⭐解决方法 🌺…...
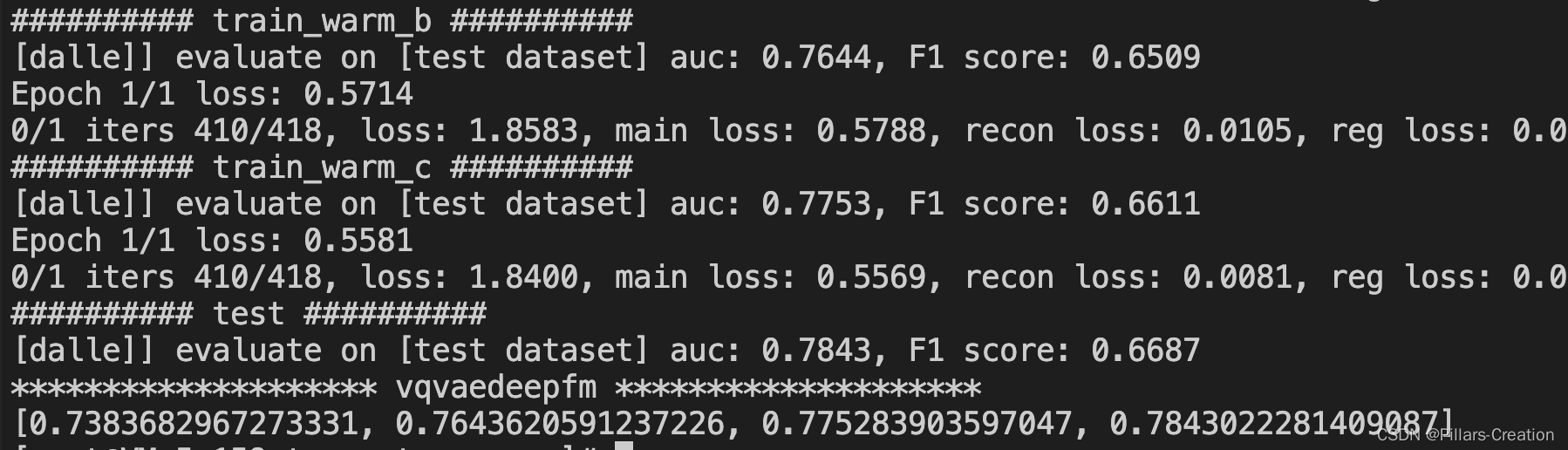
vqvae简单实战,利用vqvae来提升模型向量表达
最近CV领域各种大模型在图像生成领域大发异彩,比如这两年大火的dalle系列模型。在这些模型中用到一个基础模型vqvae,今天我们写个简单实现来了解一下vqvae的工作原理。vqvae原始论文连接https://arxiv.org/pdf/1711.00937.pdf 1,代码 首先我们…...
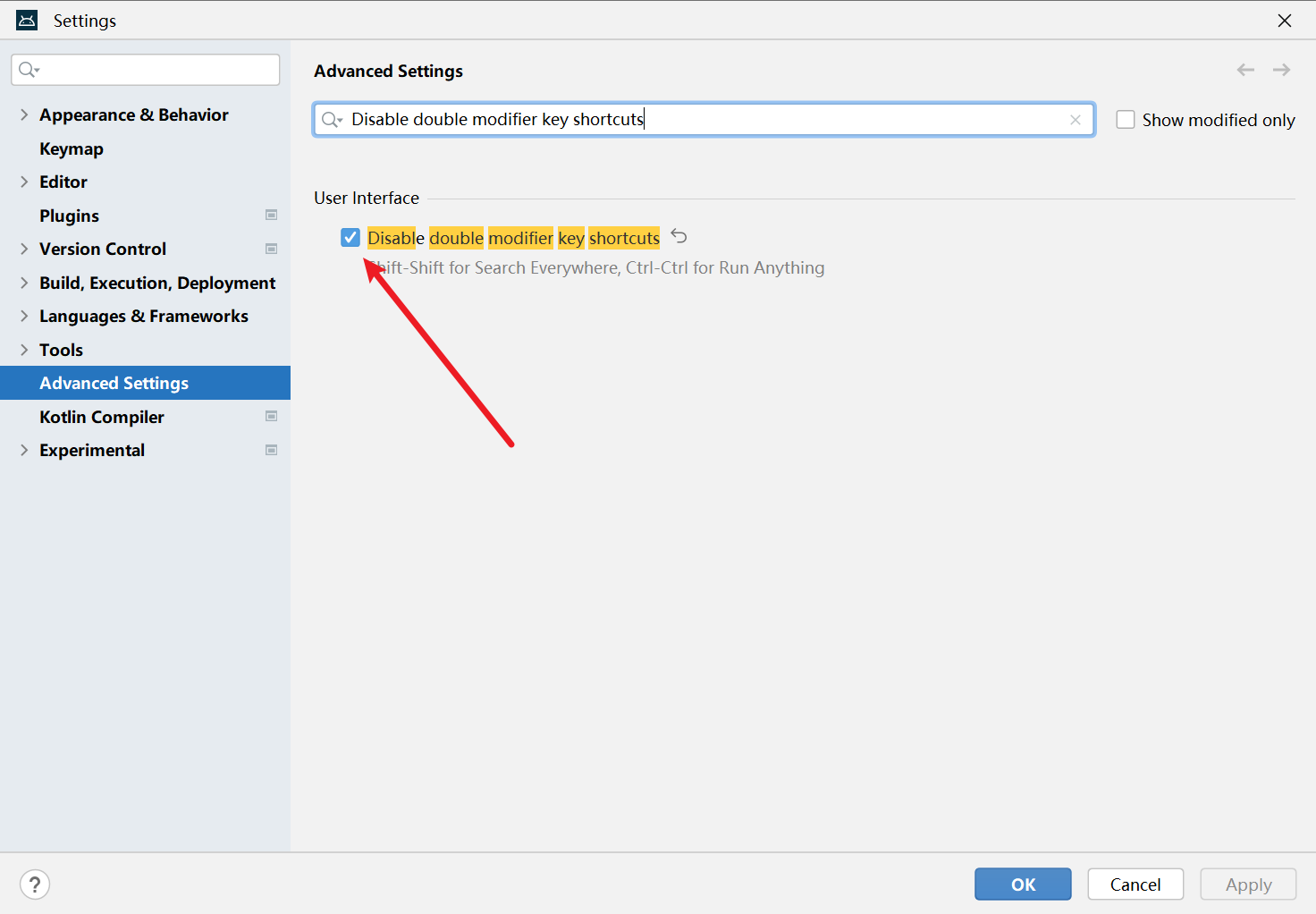
idea禁用双击ctrl
Run anything | IntelliJ IDEA Documentation Disable double modifier key shortcuts...
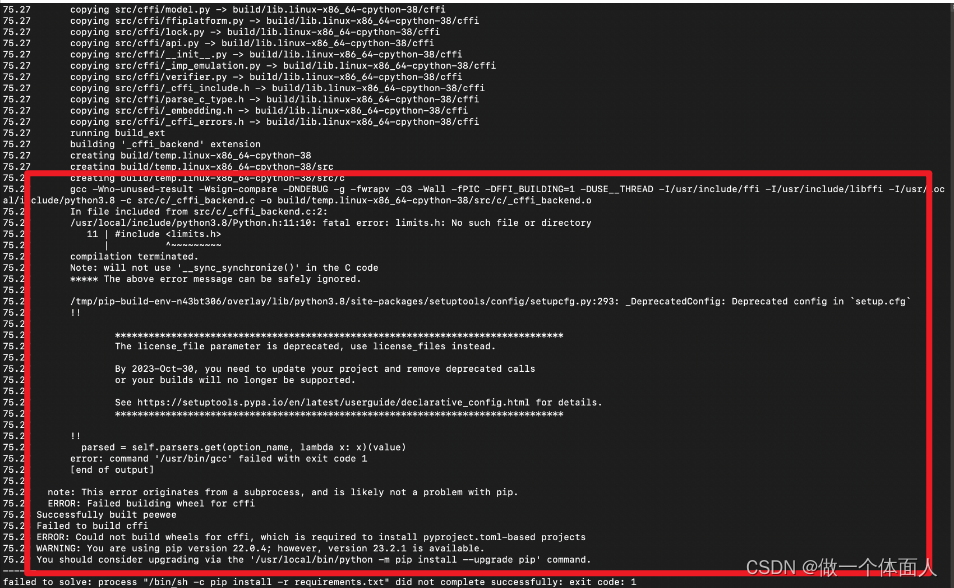
记使用docker部署项目出现问题
我的docker-compose.yml内容如下: version: "3" services:my_server:build: .restart: alwaysdepends_on:mysql:condition: service_startedports:- 9999:9999links:- mysqlmysql:image: mysql:latest # mysql:oraclerestart: alwayscontainer_name: mys…...

EDU挖掘
1.信息搜集2.漏洞挖掘 1.信息搜集 没事干,准备找个证书站挖挖看,没想到碰到一个小通用系统。 看样子还挺多功能可以测, 这里利用F12 查看前端源码js 或者css文件,直接用hunter或者fofa搜索到同一类型的网站。 Hunter语法&#…...

机器人制作开源方案 | 杠杆式6轮爬楼机器人
1. 功能描述 本文示例将实现R281b样机杠杆式6轮爬楼机器人爬楼梯的功能(注意:演示视频中为了增加轮胎的抓地力,在轮胎上贴了双面胶,请大家留意)。 2. 结构说明 杠杆式6轮爬楼机器人是一种专门用于爬升楼梯或不平坦地面…...

报错——warning: ignoring JAVA_HOME=/home/jdk/jdk1.8.0_281; using bundled JDK
我使用了es的8.3.0版本,但es从7.17版本以后不再支持jdk1.8了,需要进行JDK的版本升级,或者降低es的版本。 es和jdk对比版本...

【Java8】java.time 根据日期获取年初年末、月初月末、日初日末
目录 年初年末月初月末3. 日初日末 记录日常开发中的常用的日期转换代码,算是一篇Java 8时间API使用实操的简短总结文。 下文中,都以LocalDateTime为例,在不声明的情况下如下方法一般都适用于Java8中LocalDate、LocalDateTime、OffsetDateTi…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
