redis作为消息队列的缺点

Redis作为消息队列的不足。
1、基于内存
Redis是一种基于内存的数据库产品,这意味着数据存储在内存中,当内存不足时,Redis会使用基于磁盘的虚拟内存来存储数据。虽然这种虚拟内存机制可以增加Redis的存储容量,但也会降低Redis的性能和可靠性。
2、存储容量有限
Redis的存储容量受内存容量的限制,如果需要存储大量的数据,需要购买更多的内存,这会增加成本。如果内存容量不足,Redis就需要使用虚拟内存,导致性能下降和数据可靠性降低。
3、不支持多消费者同时处理消息
当多个消费者同时处理消息时,就会涉及到并发和数据一致性等问题。Redis的列表数据结构虽然可以支持多个消费者同时消费,但是需要借助其他的方式来保证并发和数据一致性。
4、监控和调试不方便
Redis是一种基于内存的数据库,数据库中的数据是存储在内存中的,这会导致监控和调试变得非常困难。如果需要进行监控和调试,需要借助其他的工具和技术。
5、总结
作为一种高性能的NoSQL数据库产品,Redis在消息队列场景中具有诸多优势和不足。Redis的高性能、多种数据结构支持、多语言支持和可靠性高等优点可以满足高并发、高吞吐量的应用需求,但是Redis也存在存储容量有限、不支持多消费者同时处理消息等不足之处。在实际使用中,需要根据具体的应用场景来选择合适的消息队列方案,综合考虑Redis的优缺点,才能够更好地应用Redis作为消息队列来处理数据。
相关文章:

redis作为消息队列的缺点
Redis作为消息队列的不足。 1、基于内存 Redis是一种基于内存的数据库产品,这意味着数据存储在内存中,当内存不足时,Redis会使用基于磁盘的虚拟内存来存储数据。虽然这种虚拟内存机制可以增加Redis的存储容量,但也会降低Redis的…...

Redis五大数据类型的底层设计
SDS 无论是 Redis 的 Key 还是 Value,其基础数据类型都是字符串。虽然 Redis是使用标准 C 语言开发的,但并没有直接使用 C 语言中传统的字符串表示,而是自定义了一 种字符串。这种字符串本身的结构比较简单,但功能却非常强大&…...

logback的简单配置详解
<?xml version"1.0" encoding"UTF-8"?> <!--logback配置的根元素。scantrue表示logback将定期扫描配置文件以检测更改。scanPeriod"30 Period" 扫描间隔为30s--> <configuration scan"true" scanPeriod"30 seco…...

TatukGIS Developer Kernel使用教程:如何为FMX创建第一个应用程序
概述:TatukGIS Developer Kernel(DK)是一个用于开发自定义地理信息系统(GIS)应用程序以及解决方案的综合性软件开发工具包(SDK)。本篇文章主要介绍用DK11为FMX创建一个应用程序,现在…...
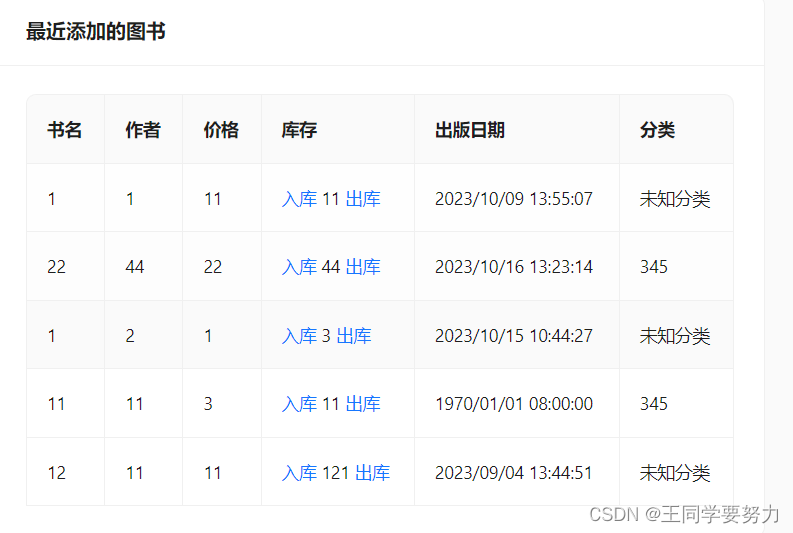
Ant Design Vue设置表格滚动 宽度自适应 不换行
Ant Design Vue设置表格滚动 宽度自适应 不换行 添加以下属性即可解决这个问题: <a-table :columns"columns" :data-source"list":pagination"false"bordered:scroll"{ x: max-content }" >...

在Linux上开启文件服务,需要安装并配置Samba
在Linux上开启文件服务,需要安装并配置Samba。以下是具体步骤: 安装Samba软件包:在终端中输入以下命令进行安装: 复制代码 sudo apt-get update && sudo apt-get install samba 配置Samba:编辑Samba配置文件…...

TypeScript 类型兼容性
TypeScript 类型兼容性 在前端开发中,使用 TypeScript 可以提供更强大的类型检查和类型安全。然而,了解 TypeScript 中的类型兼容性是至关重要的,因为它涉及如何处理不同类型之间的关系,以及在这些类型之间进行无缝的交互。本文将…...

【多线程】线程的状态
我们可以通过下面的这段代码来查看线程一共有哪几种状态 //线程的状态是一个枚举类型 Thread.State for(Thread.State state : Thread.State.values()){System.out.println(state); }NEW(新建状态): 当线程对象已经被创建,但是 s…...

pytorch 对图片进行归一化处理
如题,神经网络通常使用浮点数张量作为输入,我们要做的第一件事情就是将图片转化为浮点数,并且做归一化操作。 import torch import imageio import osdata_dirF:\\work\\deep_learning\\pytorch\\dlwpt-code-master\\data\\p1ch4\\image-cat…...

零售数据分析师熬夜整理:人、货、场、供、财这样做
在零售数据分析中,人、货、场、供、财数据分析非常重要,它们分别是指人员、商品、场所、供应和财务,对这些要素进行数据分析,可以更好地了解市场需求、优化商品供应链、调整销售策略和提高盈利能力。零售数据量大、分析指标多且复…...
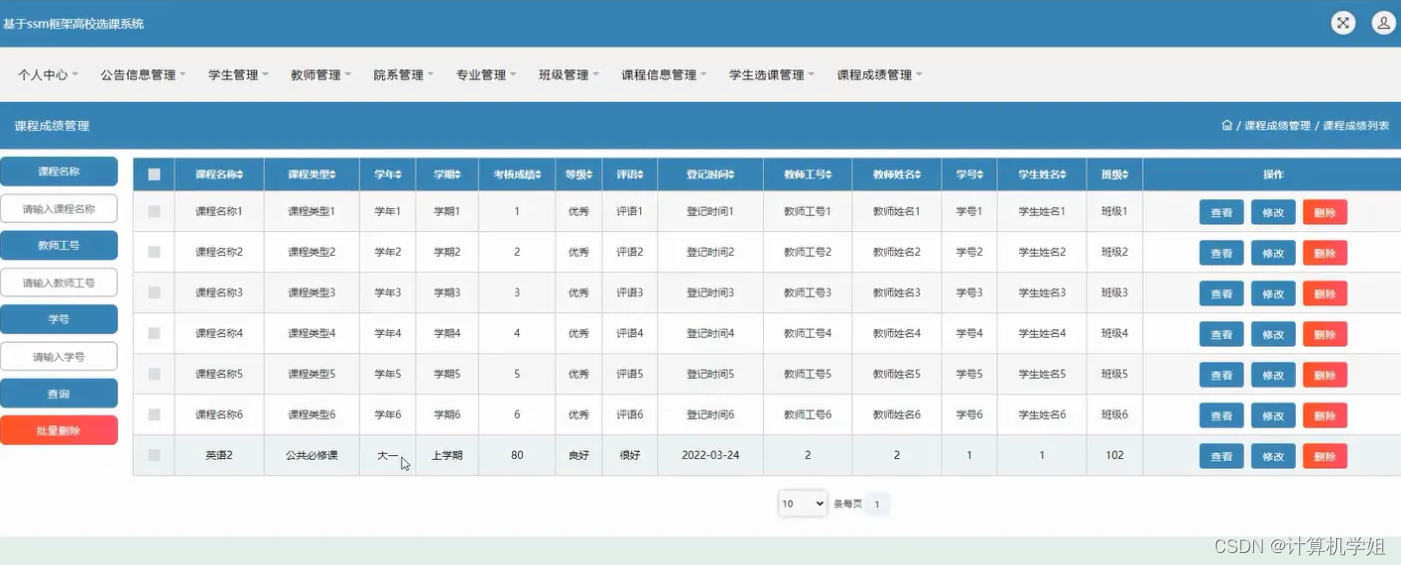
基于SSM的学生选课管理系统
基于SSM的高校校园学生选课系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 登录界面 专业管理 教师管理 课程管理 成绩管理 摘要 基于SSM的学生选课管…...

SQL注入漏洞
0x01 漏洞介绍 泛微e-office系统是标准、易用、快速部署上线的专业协同OA软件,国内协同OA办公领域领导品牌,致力于为企业用户提供专业OA办公系统、移动OA应用等协同OA整体解决方案。泛微e-office深谙改革之道以迎变革之机,沉心产品研发数十载…...

C++ wpf自制软件打包安装更新源码实例
程序示例精选 C wpf自制软件打包安装更新源码实例 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对《C wpf自制软件打包安装更新源码实例》编写代码,代码整洁,规则&…...
8月19日PMP成绩,预计10月16日公布!附查询入口、流程
PMP的考试成绩一般在考后6-8周即可查询,8月PMP的成绩预计会在北京时间10月16日晚上公布,具体时间以官方公告为准。 如何查询8月考试成绩? 渠道一:收到PMI邮件提醒 当你注册PMI所使用的邮箱收到一封PMI发来的,标题为…...

简易LDO设计(包含原理图、PCB和实验)
一、前置知识 ①该电路是通过三极管(BJT)来实现的,所以需要知晓三极管的工作原理和特性。 ②三极管有三种状态:放大、饱和、截止。本文是利用三极管的放大状态来模拟LDO芯片的功能。 二、原理图 ①稳压二极管要想稳定到某个电压范…...

SpringBoot面试题5:SpringBoot Starter的工作原理是什么?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:SpringBoot Starter的工作原理是什么? Spring Boot Starter 是一种便捷的方式来为 Spring Boot 应用程序引入一组特定功能的依赖项。它简化了项目…...

Leetcode 2902. Count of Sub-Multisets With Bounded Sum
Leetcode 2902. Count of Sub-Multisets With Bounded Sum 1. 解题思路2. 代码实现3. 算法优化 题目链接:2902. Count of Sub-Multisets With Bounded Sum 1. 解题思路 这一题有点惭愧,因为没有搞定,遇上了超时问题…… 我的思路其实还是…...
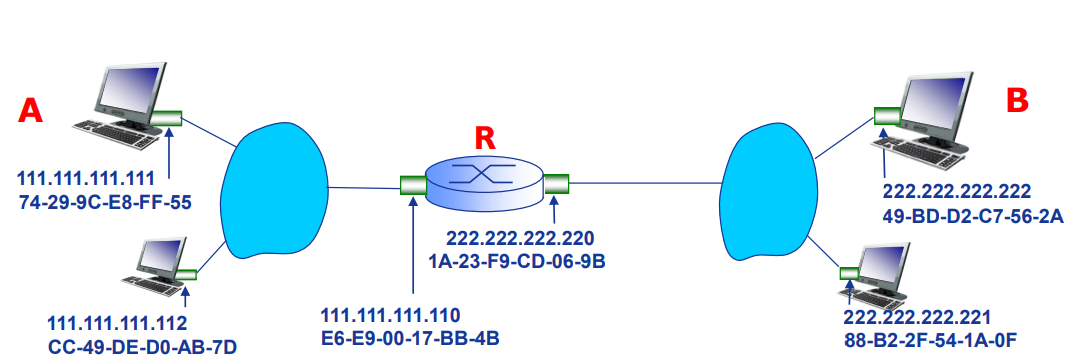
ARP协议(地址解析协议) 的作用和操作过程
目录 1.问题: (在同一个LAN局域网内)如何在已知目的接口的IP地址前提下确定其MAC地址?2.问题:现在假设主机A要向目的主机B发送一个数据报,怎么发送呢?2.1在一个局域网内时2.1.1情况一:2.1.2情况…...
轻游戏风格虚拟资源付费下载模板Discuz论坛模板
轻游戏风格虚拟资源付费下载模板Discuz论坛模板,游戏资讯付费VIP源码模板。 模板说明: 1、模板名称:"qing游戏风格",版本支持:discuzx3.0版本,discuzx3.1版本,discuzx3.2版本&#…...

MongoDB索引操作
1、创建索引 语句: db.collection.createIndex(keys, options, commitQuorum) 选项参数名类型描述keys 包含排序字段和排序方式的对象, 值: 1为升序索引 -1为降序索引 options参数控制对象backgroundboolean 可选࿰…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
