leetcode221.最大正方形
最大正方形
可以使用动态规划降低时间复杂度。用 dp(i,j) 表示以 (i,j)为右下角,且只包含 111 的正方形的边长最大值。能计算出所有 dp(i,j)的值,那么其中的最大值即为矩阵中只包含 111 的正方形的边长最大值,其平方即为最大正方形的面积。
如果该位置的值是 0,则 dp(i,j)=0,因为当前位置不可能在由 111 组成的正方形中;
如果该位置的值是 111,则 dp(i,j)的值由其上方、左方和左上方的三个相邻位置的 dp值决定。具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加 111,状态转移方程如下:
dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1
其中1277. 统计全为 1 的正方形子矩阵的官方题解给出了详细的证明。
此外,还需要考虑边界条件。如果 i 和 j中至少有一个为 0,则以位置 (i,j)为右下角的最大正方形的边长只能是 1,因此 dp(i,j)=1。
#include<bits/stdc++.h>
using namespace std;
//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {int m = matrix.size();int n = matrix[0].size();int dp[m][n];for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {dp[i][j] = -1;}}int ans = 0;for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (matrix[i][j] == '0'){dp[i][j] = 0;continue;}if (i == 0 || j == 0){dp[i][j] = 1;}else{dp[i][j] = min(min(dp[i][j - 1], dp[i - 1][j - 1]), dp[i - 1][j]) + 1;}ans = max(ans, dp[i][j]);}}return ans * ans;}
};
//leetcode submit region end(Prohibit modification and deletion)int main(){Solution s;vector<vector<char>> num = {{'1', '0', '1', '0', '0'}, {'1', '0', '1', '1', '1'}, {'1', '1', '1', '1', '1'}, {'1', '0', '0', '1', '0'}};int a = s.maximalSquare(num);cout<<(a);return 0;
}
相关文章:

leetcode221.最大正方形
最大正方形 可以使用动态规划降低时间复杂度。用 dp(i,j) 表示以 (i,j)为右下角,且只包含 111 的正方形的边长最大值。能计算出所有 dp(i,j)的值,那么其中的最大值即为矩阵中只包含 111 的正方形的边长最大值,其平方即为最大正方形的面积。 …...

低代码技术这么香,如何把它的开发特点发挥到极致?
前言 什么是低代码技术? 低代码是一种可视化软件开发方法,通过最少的编码更快地交付应用程序。图形用户界面和拖放功能使开发过程的各个方面自动化,消除了对传统计算机编程方法的依赖。 文章目录 前言低代码平台怎么选?用友Yonbu…...
drawio简介以及下载安装
drawio简介以及下载安装 drawio是一款非常强大的开源在线的流程图编辑器,支持绘制各种形式的图表,提供了 Web端与客户端支持,同时也支持多种资源类型的导出。 访问网址:draw.io或者直接使用app.diagrams.net直接打开可以使用在线版…...
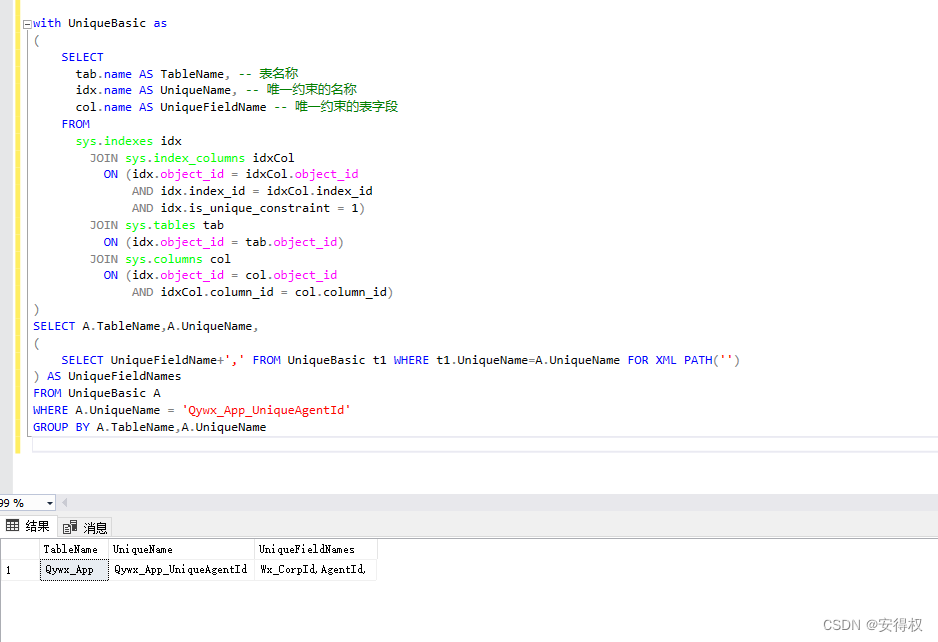
Sql Server 数据库中的所有已定义的唯一约束 (列名称 合并过了)
查询Sql Server Database中的唯一约束 with UniqueBasic as (SELECTtab.name AS TableName, -- 表名称idx.name AS UniqueName, -- 唯一约束的名称col.name AS UniqueFieldName -- 唯一约束的表字段FROMsys.indexes idxJOIN sys.index_columns idxColON (idx.object_id idxCo…...
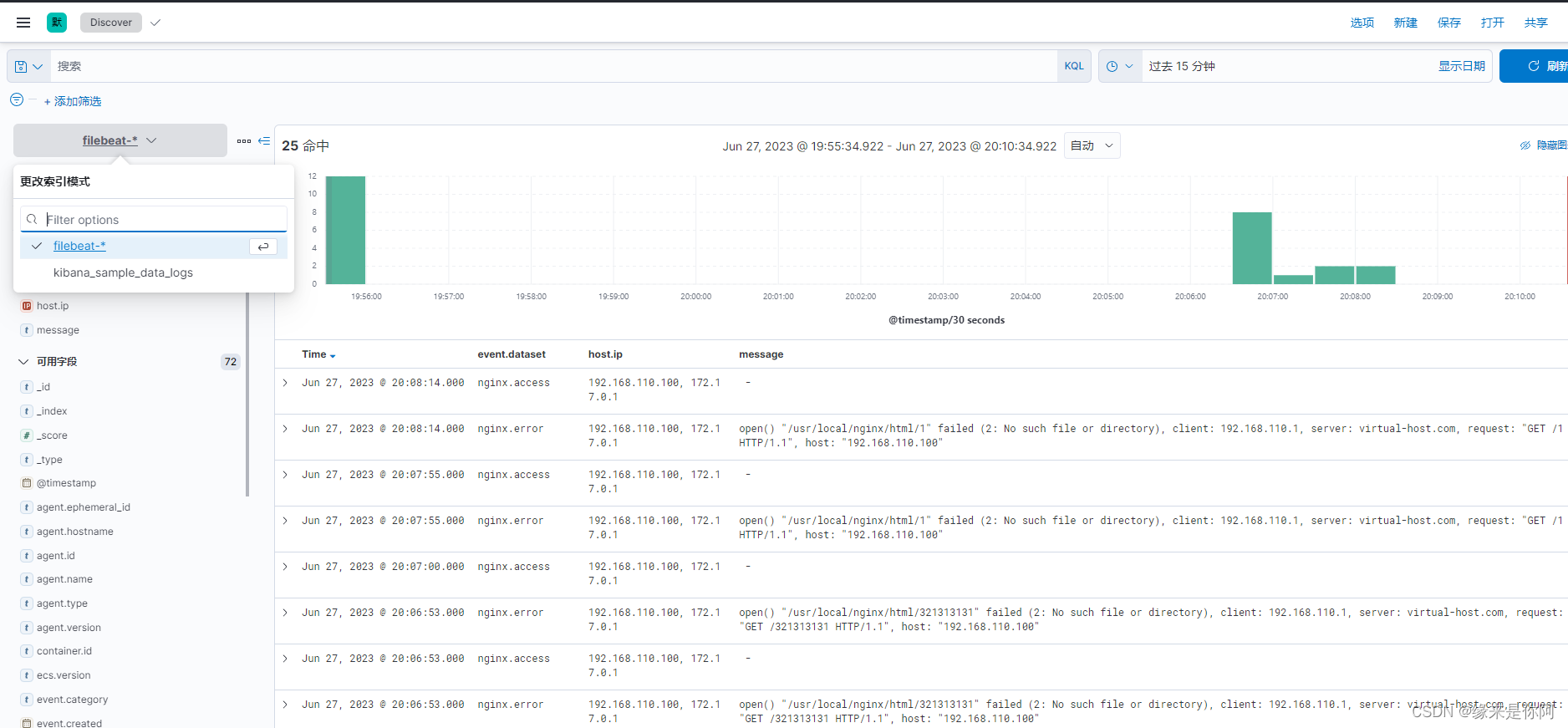
elasticsearch (六)filebeat 安装学习
filebeat 安装:文件节拍快速入门:安装和配置 |文件节拍参考 [7.17] |弹性的 (elastic.co) 解压缩后,以配置nginx日志为例。 Nginx module | Filebeat Reference [7.17] | Elastic filebeat 配置中, - module: nginx access: …...

算法通关村第一关|青铜|链表笔记
1.理解 Java 如何构造出链表 在 Java 中,我们创建一个链表类,类中应当有两个属性,一个是结点的值 val ,一个是该结点指向的下一个结点 next 。 next 通俗讲是一个链表中的指针,但是在链表类中是一个链表类型的引用变量…...

【记录】使用Python读取Tiff图像的几种方法
文章目录 PIL.Imagecv2gdal 本文总结了使用 PIL Image, cv2, gdal.Open三种python package 读取多通道Tiff格式遥感影像的方法。 PIL.Image PIL对Tiff只支持两种格式的图像: 多通道8bit图像单通道int16, int32, float32图像 多通道多bit的tiff图像PIL不支持读取…...

JOSEF约瑟 多档切换式漏电(剩余)继电器JHOK-ZBL1 30/100/300/500mA
系列型号: JHOK-ZBL多档切换式漏电(剩余)继电器(导轨) JHOK-ZBL1多档切换式漏电(剩余)继电器 JHOK-ZBL2多档切换式漏电(剩余)继电器 JHOK-ZBM多档切换式漏电…...

Linux部署kubeedge 1.4
文章目录 一、机器信息二、环境准备(所有节点操作)2.1. 修改主机名2.2. 开启路由转发2.3.安装Docker(所有节点)2.4.部署K8S集群(单机版,云端节点) 2.5.安装Mosquitto(只在边缘节点安装)三、安装kubeedge 1.…...

第一章习题
文章目录 x ( t ) j e j w 0 t x(t)je^{jw_0t} x(t)jejw0t x [ n ] j e j w 0 n x[n]je^{jw_0n} x[n]jejw0n 求基本周期: T 2 Π w 0 T\frac{2Π}{w_0} Tw02Π 对x[n],T为有理数才算 1、求信号x(t)2cos(10t1)-sin(4t-1)的基波周期 2 Π 10 Π 5 \frac{2…...
nvm、node、npm解决问题过程记录
在Windows10如何降级Node.js版本:可以尝试将Node.js版本降级到一个较旧的版本,以查看问题是否得以解决。可以使用Node Version Manager (nvm) 来轻松切换Node.js版本,具体完整步骤: 首先,需要安装Node Version Manager…...

Linux- DWARF调试文件格式
基本概念 DWARF是一个用于在可执行程序和其源代码之间进行关联的调试文件格式。当开发者使用调试编译选项(例如,使用gcc时的-g标志)编译程序时,编译器会生成这种格式的调试信息。这些信息在后续的调试过程中非常有用,…...
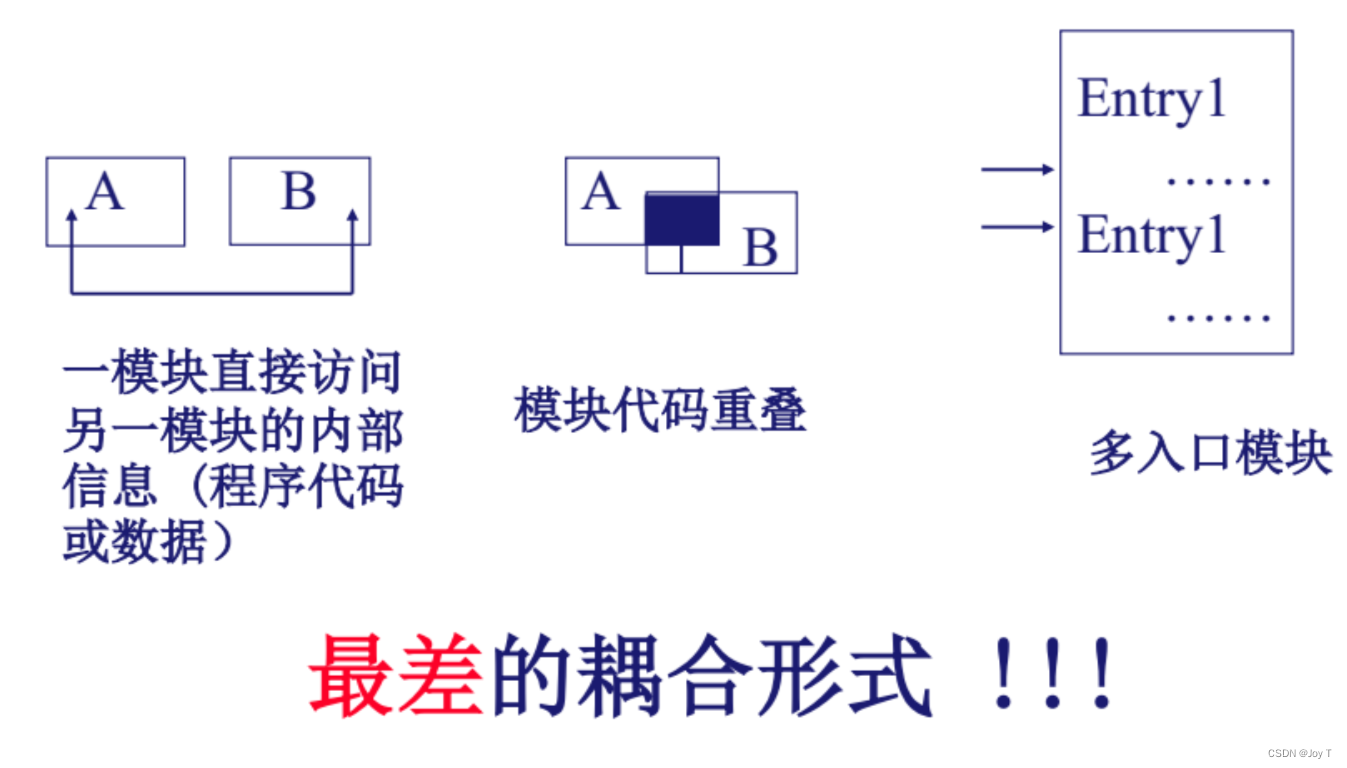
软件工程第六周
软件体系结构概述 体系结构:一种思想,而框架就是思想的实现,设计模式就是根据某一特殊问题实现的框架。 体系结构:体系结构是软件系统的高级结构。它定义了系统的主要组成部分,以及这些部分之间的关系和交互方式。 框…...

node+pm2安装部署
1、安装node 下载node安装包: wget https://nodejs.org/dist/v16.14.0/node-v16.14.0-linux-x64.tar.xz 解压: tar -xvJf node-v14.17.0-linux-x64.tar.xz 配置环境变量,在/etc/profile文件最后添加以下脚本: export PATH$P…...
-hive on mapreduce详解)
大数据学习(11)-hive on mapreduce详解
&&大数据学习&& 🔥系列专栏: 👑哲学语录: 承认自己的无知,乃是开启智慧的大门 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一下博>主哦&#x…...

MyBatis基础之自动映射、映射类型、文件注解双配置
文章目录 自动映射原理jdbcType同时启用配置文件和注解两种配置方式 自动映射原理 在 MyBatis 的配置文件(settings 元素部分)中,有一个 autoMappingBehavior 配置,其默认值为 PARTIAL ,表示 MyBatis 会自动映射&…...

8、docker 安装 nginx
1、下载镜像 docker pull nginx 2、本机创建目录 1)创建nginx挂载目录 mkdir /usr/local/nginx 2)进入nginx目录 cd /usr/local/nginx 3)创建 www和logs目录 mkdir -p www logs 3、创建nginx容器 此容器用于复制配置文件,复…...
关于Skywalking Agent customize-enhance-trace对应用复杂参数类型取值
对于Skywalking Agent customize-enhance-trace 大家应该不陌生了,主要支持以非入侵的方式按用户自定义的Span跟踪对应的应用方法,并获取数据。 参考https://skywalking.apache.org/docs/skywalking-java/v9.0.0/en/setup/service-agent/java-agent/cust…...

手机路径、Windows路径知识及delphiXE跨设备APP自动下载和升级
手机路径、Windows路径知识 及delphiXE跨设备APP自动下载和升级 一、APP安装程序文件版本和权限信息 1、运行时动态调用Android apk的AndroidManifest.xml获取versionName 2、运行时动态调用IOS ipa的info.plist获取CFBundleVersion (和entitlements)…...

GitLab 502问题解决方案
由于最近 gitlab 切换到另一台服务器上部署的 gitlab 后,经常出现 502。平时重启 gitlab 后都能解决,今天突然重启多次后都还是 502(重启日志是正常的),遂通过 gitlab-ctl tail 查看日志进行排查。 gitlab-ctl tail通…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
