高效工具类软件使用
高效工具类软件使用
- 目录
- 概述
- 需求：
- 设计思路
- 实现思路分析
- 1.Leanote
- 2.Obsidian 的使用
- 参考资料和推荐阅读
Survive by day and develop by night.
talk for import biz , show your perfect code,full busy，skip hardness,make a better result,wait for change,challenge Survive.
happy for hardess to solve denpendies.
目录
概述
高效工具类软件使用
需求：
设计思路
实现思路分析
1.Leanote
Leanote 二进制版详细安装教程 Windows
下载 leanote 二进制版。
安装 mongodb。
导入初始数据。
配置 leanote。
运行 leanote。
2.Obsidian 的使用
这个不错，可以导出pdf 等格式的文件。
这2者都可以作为的本地笔记使用。
###3.其他就是云盘的使用
网盘的使用等了
参考资料和推荐阅读
参考资料
官方文档
开源社区
博客文章
书籍推荐
- https://github.com/leanote/leanote/wiki/Leanote-%E4%BA%8C%E8%BF%9B%E5%88%B6%E7%89%88%E8%AF%A6%E7%BB%86%E5%AE%89%E8%A3%85%E6%95%99%E7%A8%8B----Windows
欢迎阅读，各位老铁，如果对你有帮助，点个赞加个关注呗！同时，期望各位大佬的批评指正~
相关文章：
高效工具类软件使用
高效工具类软件使用 目录概述需求： 设计思路实现思路分析1.Leanote2.Obsidian 的使用 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy，skip hardness,make a better result,wait for…...
批处理文件（.bat）中，dir与tree命令的效果
目录 dir命令 用法 操作 效果 dir /? dir dir D:\111\111_3 dir D:\111 *.mp4 dir D:\111 /ad dir D:\111 /ar dir D:\111 /s dir D:\111\111_3 >1bat.txt dir D:\111 >>1bat.txt tree命令 用法 操作 效果 tree /? tree tree D:\111\111_3 tree…...
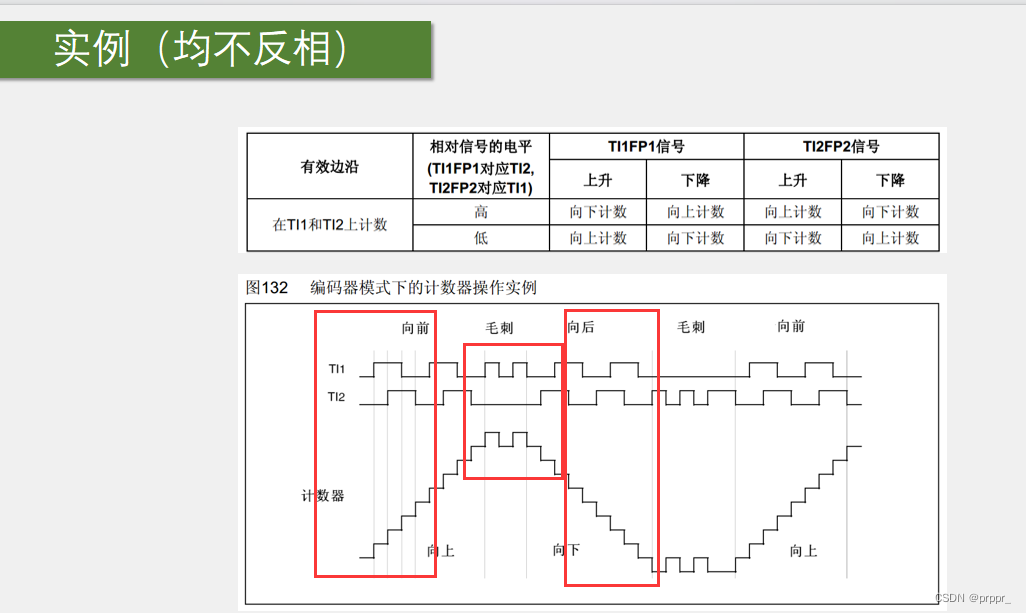
STM32 ---- 再次学习STM32F103C8T6/STM32F409IGT6
目录 一、环境搭建及介绍 关于STM32基础介绍 新建工程 外设案例 LED流水灯 蜂鸣器 上拉电阻和下拉电阻知识 电压比较器 c语言基础知识 类型、结构体、枚举 类型int8_t int16_t int32_t 宏替换 #define 和typedef用法 结构体两种填充方法 和 命名规则 枚举用法 常用…...
UE4 EQS环境查询 学习笔记
EQS环境查询对应Actor的范围 EQS环境查询查询对应的类 查询到即有一个蓝色的球在Actor上，里面有位置信息等等 在行为树运行EQS，按键（‘）可以看到Player的位置已经被标记 运行对应的EQS在这里放如EQS就可以了 Generated Point&…...
计算机算法分析与设计（11）---贪心算法(活动安排问题和背包问题)
文章目录 一、贪心算法概述二、活动安排问题2.1 问题概述2.2 代码编写 三、背包问题3.1 问题描述3.2 代码编写 一、贪心算法概述 1. 贪心算法的定义：贪心算法是指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以…...
shell命令以及运行原理
Linux严格意义上说的是一个操作系统，我们称之为“核心（kernel）“ ，但我们一般用户，不能直接使用kernel。 而是通过kernel的“外壳”程序，也就是所谓的shell，来与kernel沟通。如何理解&a…...
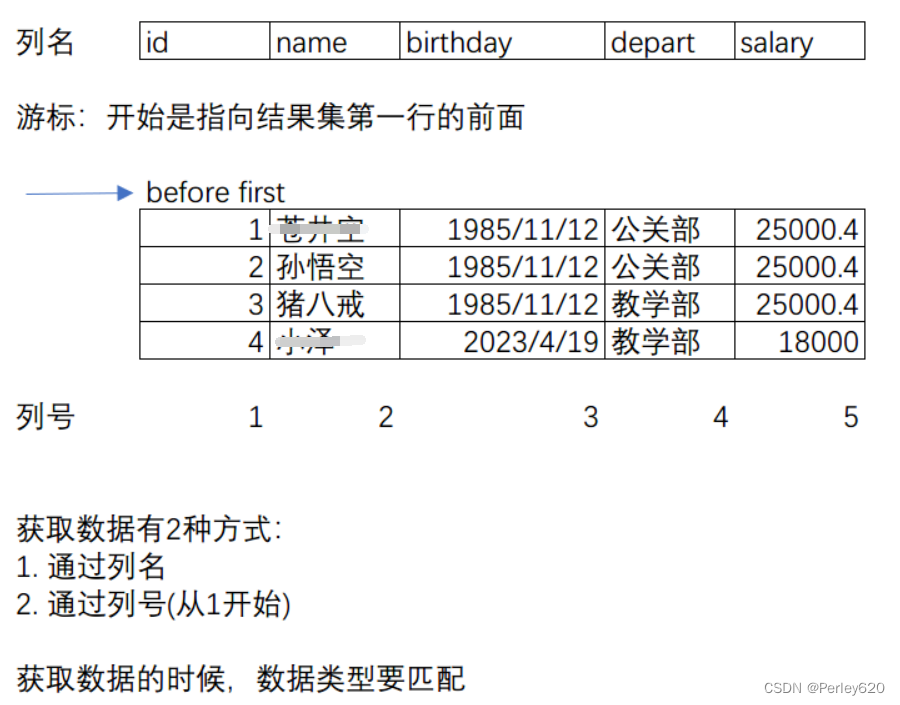
MySQL进阶（再论JDBC）——JDBC编程思想的分析 JDBC的规范架构 JDBC相关的类分析
前言 SQL（Structured Query Language）是一种用于管理关系型数据库的标准化语言，它用于定义、操作和管理数据库中的数据。SQL是一种通用的语言，可以用于多种关系型数据库管理系统（RDBMS），如MySQ…...
rabbitMQ的知识点
RabbitMQ是一种消息队列软件，它实现了高度可靠的消息传递机制。RabbitMQ支持多种消息协议，包括AMQP、STOMP、MQTT等，比较灵活。以下是一些rabbitmq的知识点： 1. 消息队列：消息队列是一种分布式系统中广泛使用的通信模…...
EtherNet/IP 库卡机器人和EtherCAT倍福PLC总线协议连接案例
EtherNet/IP 是一种适合于工业环境和对时间要求比较苛刻的应用的网络。而远创智控YC-EIPM-ECT通讯网关，是一款自主研发的EtherNet/IP 从站功能的通讯网关。它不仅可以实现EtherNet/IP 和EtherCAT的无缝连接，还可以将EtherNet/IP 作为从站连接到EtherCAT总…...
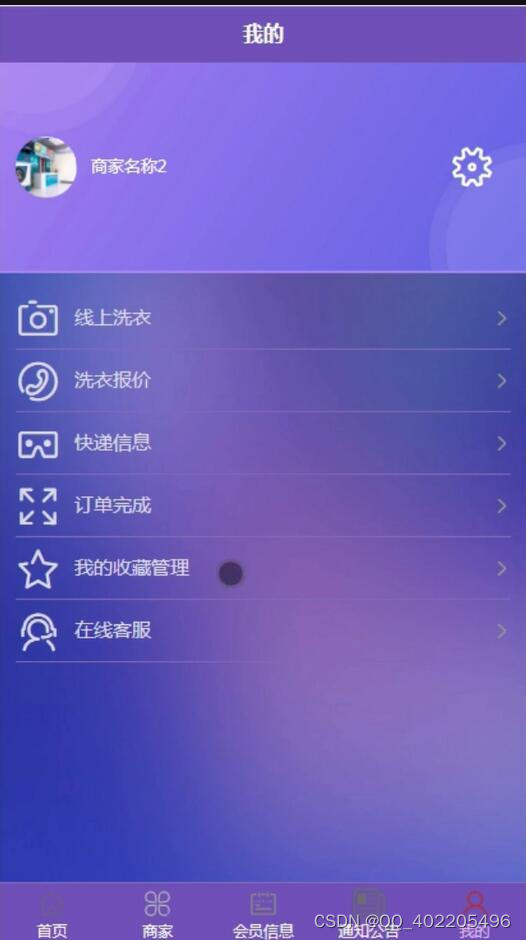
微信小程序 uniapp+vue线上洗衣店业务管理系统演89iu2
本课题意在设计一种系统的、基于用户体验的线上洗衣服务模式，具有如下的研究意义: (1)为用户提供更简单、便捷的洗衣服务模式; (2)为智能柜的盈利模式提供了新的方向; (3)通过线上系统、智能柜与洗衣工厂结合的方式，为洗衣企业构建了一套节 省人力成本的…...
Maven项目，进行编译，使用idea的 编译功能，就是正常的，但是在终端中执行 mvn clean compile 报错
一、背景： Maven项目，进行编译，使用idea的 编译功能，就是正常的，但是在终端中执行 mvn clean compile 报错 报错信息： [ERROR] Failed to execute goal org.apache.maven.plugins:maven-compiler-plugin…...
mssql还原数据库失败
标题: Microsoft SQL Server Management Studio ------------------------------ 服务器 "192.168.31.132" 的 附加数据库 失败。 (Microsoft.SqlServer.Smo) 有关帮助信息，请单击: https://go.microsoft.com/fwlink?ProdNameMicrosoftSQLServer&…...
Linux多线程编程- 无名信号量
简介 无名信号量（在 POSIX 环境下通常指 sem_t 类型的信号量）是用于同步和互斥的原语，它允许线程和进程按照预期的顺序执行，并确保对共享资源的安全访问。无名信号量与命名信号量的主要区别在于它们的可见性和生命周期。无名信号…...
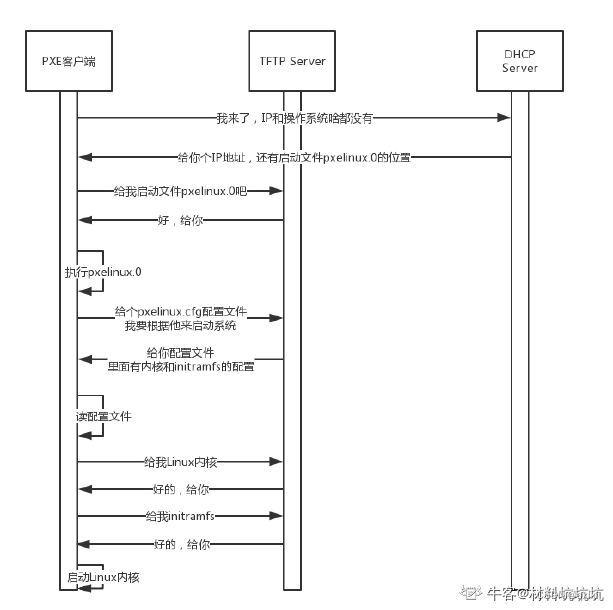
【网络协议】聊聊DHCP和PXE 工作原理
DHCP 动态主机配置协议 对于每个主机来说，只要连接了网络，那么就会配置一个IP地址，那么这个IP地址，如果是手动配置的话，对于公司内部的人员来说都要找IT进行配置，这个太浪费人力物力了，所以解决…...
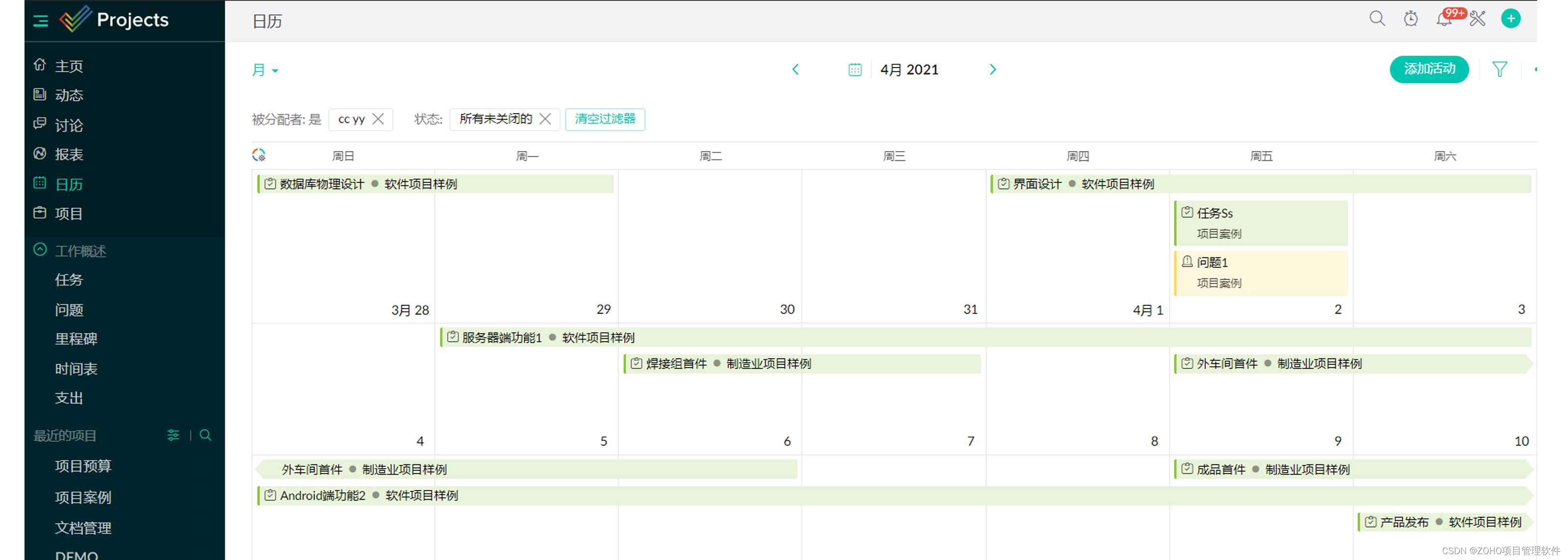
发现国内优秀的团队协作软件，帮助提高工作效率
中国有许多优秀的团队协作软件，它们在企业和组织中发挥着重要作用。 以下是一些最受欢迎的团队协作软件： 1、钉钉（DingTalk）: 这是一款由阿里巴巴推出的企业级协作工具，旨在帮助企业和组织实现高效沟通和协作。钉钉提…...
LeetCode 面试题 08.12. 八皇后
文章目录 一、题目二、C# 题解 一、题目 设计一种算法，打印 N 皇后在 N N 棋盘上的各种摆法，其中每个皇后都不同行、不同列，也不在对角线上。这里的“对角线”指的是所有的对角线，不只是平分整个棋盘的那两条对角线。 注意&#…...
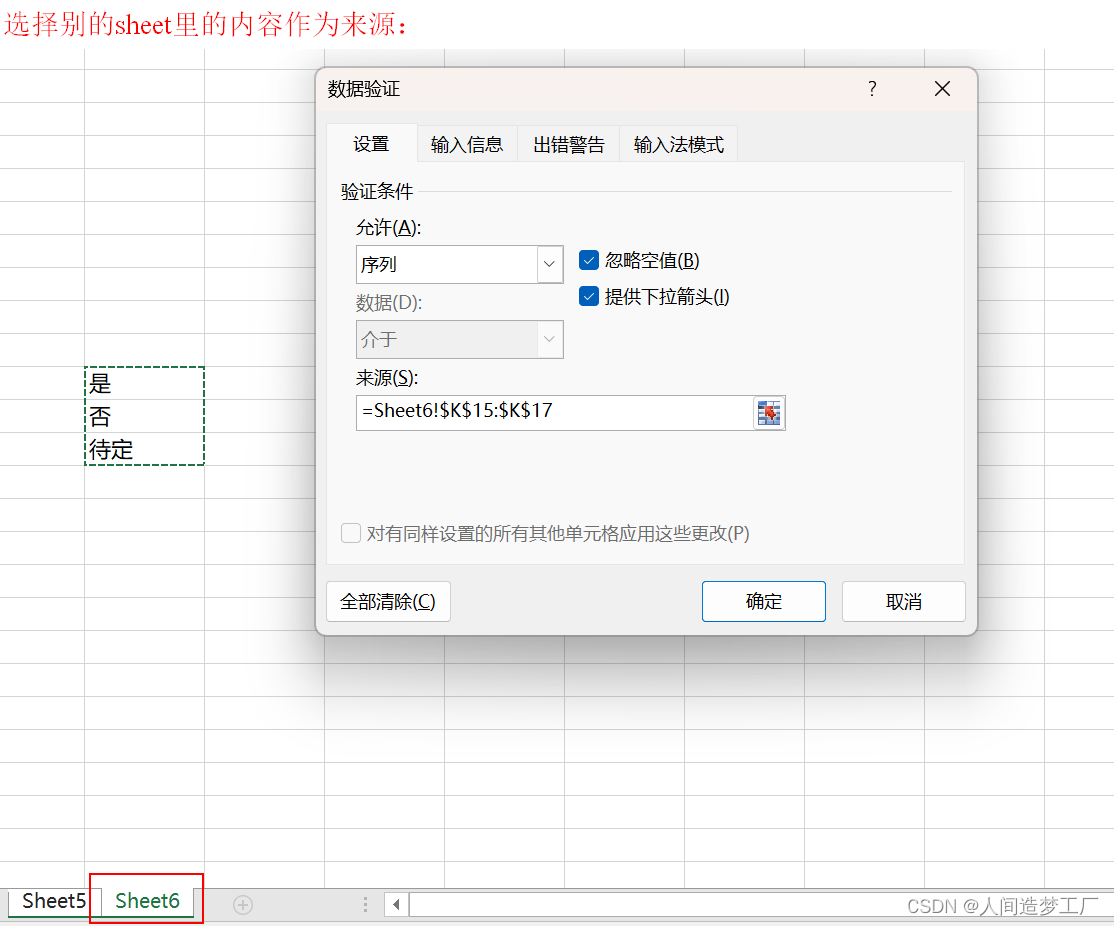
Excel 的下拉列表
可以将 Sheet6 隐藏，就更好地隐藏了来源。...
基于Effect的组件设计 | 京东云技术团队
Effect的概念起源 从输入输出的角度理解Effect https://link.excalidraw.com/p/readonly/KXAy7d2DlnkM8X1yps6L 编程中的Effect起源于函数式编程中纯函数的概念 纯函数是指在相同的输入下，总是产生相同的输出，并且没有任何副作用(side effect)的函数。…...
541. 反转字符串 II
541. 反转字符串 II class Solution { public:void Reverse(string& s, int start, int end){end--;while (start < end){swap(s[start], s[end]);start;end--;}}string reverseStr(string s, int k){int len s.size();for (int i 0; i < len; i 2 * k){if (i …...
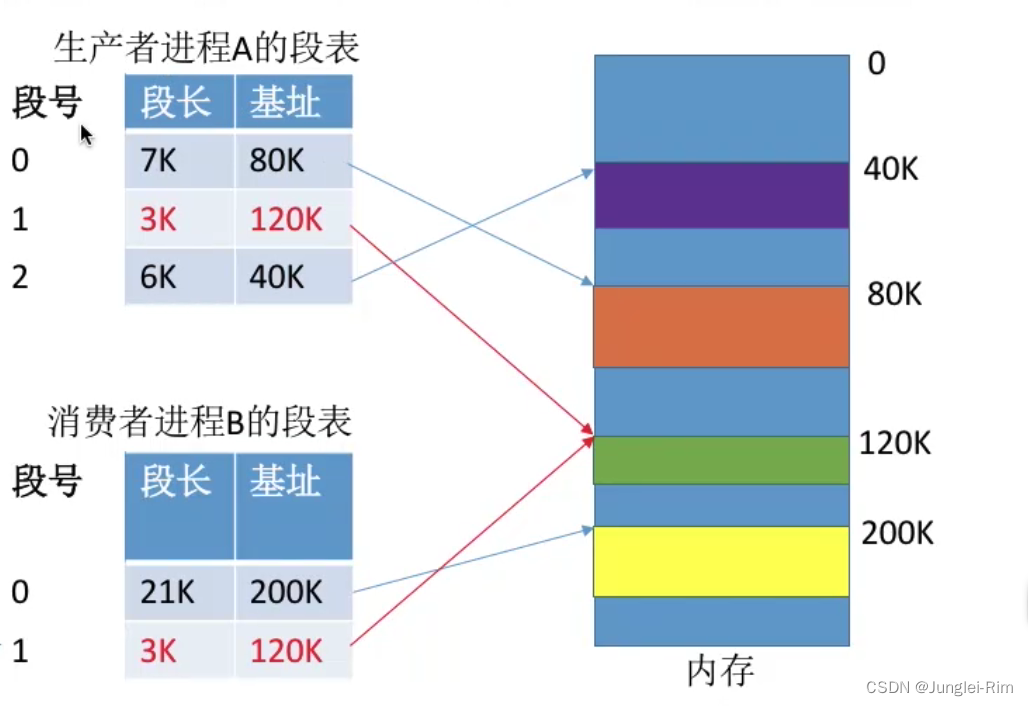
基本分段存储管理方式（分段，段表，地址转换以及与分页管理对比）
1.分段 1.进程的地址空间: 按照程序自身的逻辑关系划分为若干个段，每个段都有一个段名 （在低级语言中，程序员使用段名来编程），每段从0开始编址. 2.内存分配规则: 以段为单位进行分配，每个段在内存中占据…...
【大模型RAG】拍照搜题技术架构速览：三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道（多模态 OCR → 语义检索 → 答案渲染）、两级检索（倒排 BM25 向量 HNSW）并以大语言模型兜底”的整体框架： 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后，分别用…...
观成科技：隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具，该工具基于TUN接口实现其功能，利用反向TCP/TLS连接建立一条隐蔽的通信信道，支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式，适应复杂网…...
基于数字孪生的水厂可视化平台建设：架构与实践
分享大纲： 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年，数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段，基于数字孪生的水厂可视化平台的…...
Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了，报错如下四、启动不了，解决如下 总结 问题原因 在应用中可以看到chrome，但是打不开(说明：原来的ubuntu系统出问题了，这个是备用的硬盘&a…...
【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数（函数作为参数、返回值） 三、匿名函数与闭包1. 匿名函数（Lambda函…...
免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具，可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件，也不需要在线上传文件，保护您的隐私。 工具截图 主要特点 🚀 快速转换：本地转换，无需等待上…...
【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言： 在Java编程中，类的生命周期是指类从被加载到内存中开始，到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期，让读者对此有深刻印象。 目录 …...
给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献： stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下，文章也主…...
渗透实战PortSwigger靶场：lab13存储型DOM XSS详解
进来是需要留言的，先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码，输入的<>当成字符串处理回显到页面中，看来只是把用户输…...