力扣每日一题41:缺失的第一个正数
题目描述:
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0] 输出:3
示例 2:
输入:nums = [3,4,-1,1] 输出:2
示例 3:
输入:nums = [7,8,9,11,12] 输出:1
提示:
1 <= nums.length <= 5 * 105-231 <= nums[i] <= 231 - 1
通过次数
325.7K
提交次数
749K
通过率
43.5%
思路和题解:
设数组长度为n,则确实的第一个正数只能在[1,n+1]的闭区间
思路一:暴力搜索。时间O(n^2),空间O(1),不符合要求
依次判断[1,n]在不在数组里,如果不在就返回那个不在的数,如果都在就返回n+1。代码。
//暴力循环
class Solution {
public:int firstMissingPositive(vector<int>& nums) {int n=nums.size();for(int i=1;i<=n;i++){bool flag=false;for(int j=0;j<n;j++){if(nums[j]==i){flag=true;break;}}if(!flag) return i;}return n+1;}
};
思路二:普通的哈希表。时间O(n),空间O(n),不符合要求。
用一个长度为n的数组来标记[1,n]有没有出现过。
//普通哈希表
class Solution {
public:int firstMissingPositive(vector<int>& nums) {int n=nums.size();vector<bool> hash(n,false);for(int i=0;i<n;i++){//出现了就标记为真if(nums[i]>0&&nums[i]<=n)hash[nums[i]-1]=true;}for(int i=0;i<n;i++){if(hash[i]==false) return i+1;}return n+1;}
};思路三:原地哈希表。时间O(n),空间O(1)
思路二是我们能想到的比较好的办法了,但是空间复杂度还是不能达到要求,那我们怎么来优化这个空间复杂度O(n)呢?要知道,只用O(n)的时间复杂度,也就是只用一层的循环,要找出缺失的第一个正数的话,不用其他空间来存储正数存在的状态时不可能的。既然必须要用空间来存储一些状态,又只能额外使用常数的空间,那我们只好拿给定的数组nums作为存储状态的空间。也就是说用原数组nums作为哈希表。
问题是怎么标记一个正数是否出现的状态。对于num<=0&&num>n的数,num在[1,n]之外无论怎么变化,都不会改变答案。那就干脆先把数组里所有<=0的数先变成n+1,之后再遍历数组,把每个[1,n]内的数num对应下标处都改为负数。最后再遍历一遍数组,对应元素不为负就说明这个数对应的位置是第一个缺失的正数。
class Solution {
public:int firstMissingPositive(vector<int>& nums) {//原地哈希表//第一个缺失的数只能出现在[1,n+1]的闭区间里int n=nums.size();for(int i=0;i<n;i++){//若出现负数或零或大于n的数,那第一个确实的数就在[1,n]if(nums[i]<=0) nums[i]=n+1;}for(int i=0;i<n;i++){//将[num-1]标记为负,表示正数num没有缺失,num>n时不用管int num=abs(nums[i]);if(num<=n){nums[num-1]=-abs(nums[num-1]);}}for(int i=0;i<n;i++){if(nums[i]>0) return i+1;}return n+1;}
};
相关文章:

力扣每日一题41:缺失的第一个正数
题目描述: 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 示例 1: 输入:nums [1,2,0] 输出:3示例 2: 输…...

OpenCV与mediapipe实践
1. 安装前准备 开发环境:vscode venv 设置vscode, 建立项目,如: t1/src, 用vscode打开,新建终端Terminal,这时可能会有错误产生,解决办法: 运行命令:Set-ExecutionPolicy -ExecutionPolicy …...
【css拾遗】粘性布局实现有滚动条的情况下,按钮固定在页面底部展示
效果: 滚动条滚动过程中,按钮的位置位于手机的底部 滚动条滚到底部时,按钮的位置正常 这个position:sticky真的好用,我原先的想法是利用滚动条滚动事件去控制,没想到css就可以解决 <template><view class…...
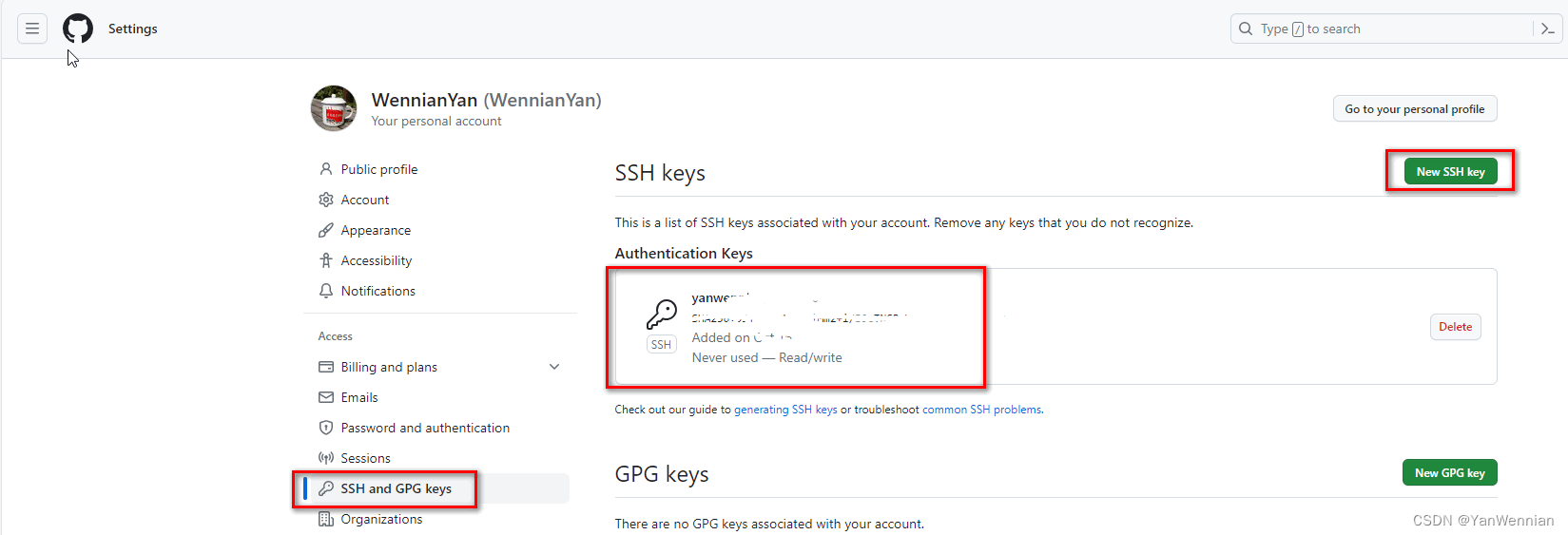
git 创建并配置 GitHub 连接密钥
前记: git svn sourcetree gitee github gitlab gitblit gitbucket gitolite gogs 版本控制 | 仓库管理 ---- 系列工程笔记. Platform:Windows 10 Git version:git version 2.32.0.windows.1 Function: git 创建并配置 GitHub…...
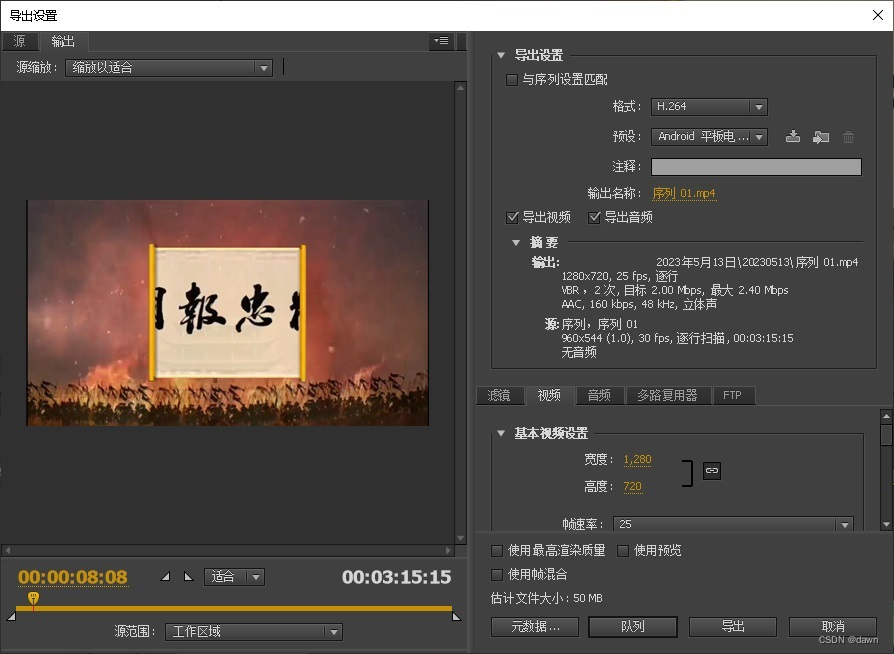
使用Premiere、PhotoShop和Audition做视频特效
今天接到一个做视频的任务,给一个精忠报国的视频,要求: ①去掉人声,就是将唱歌的人声去掉,只留下伴奏; ②截图视频中的横幅,做一个展开的效果,类似卷纸慢慢展开;…...

vueday01——动态参数
我们现在知道了 v-bind:的语法糖是: v-on:的语法糖是 我们现在来尝试一下,定义一个动态参数模拟点击事件按钮 <div :id"idValue" ref"myDiv">我是待测div{{ resultId }}</div> <button v-on:[eventName]"doSomething&…...

双向链表C语言版本
1、声明链表节点操作函数 linklist.h #ifndef LINKLIST_H__ #define LINKLIST_H__ #include <stdio.h> #include <stdlib.h> #include <stdbool.h>//#define TAIL_ADD #define HEAD_ADD typedef int LinkDataType; // 构造节点 struct LinkNode {LinkDataTy…...

visual studio安装时候修改共享组件、工具和SDK路径方法
安装了VsStudio后,如果自己修改了Shared路径,当卸载旧版本,需要安装新版本时发现,之前的Shared路径无法进行修改,这就很坑爹了,因为我运行flutter程序的时候,报错找不到windows sdk的位置,所以我…...

Motorola IPMC761 使用边缘TPU加速神经网络
Motorola IPMC761 使用边缘TPU加速神经网络 人工智能(AI)和机器学习(ML)正在塑造和推进复杂的自动化技术解决方案。将这些功能集成到硬件中,解决方案可以识别图像中的对象,分析和检测模式中的异常或找到关键短语。这些功能对于包括但不限于自动驾驶汽车…...

EM@直线的参数方程
文章目录 abstract直线参数方程从运动轨迹的角度从普通方程转换导参数方程向量法 参数方程间的转换从第3型转化为第2型方程组例 abstract 平面直线的参数方程的3种表示形式直线参数方程间的转换 直线参数方程 以下从不同角度推导直线参数方程分别记为第1,2,3形式参数方程 从…...

day08-注册功能、前端登录注册页面复制、前端登录功能、前端注册功能
1 注册功能 补充(开放文件夹内) 2 前端登录注册页面复制 4 前端注册功能 1 注册功能 # 分析前端:携带数据格式 {mobile:,code:,password}后端:-1 视图类---》注册方法-2 序列化类---》校验,保存(表中字段多,传的少---…...
rust: function
///file: nestd.rs ///ide: RustRover 233.8264.22 /// /// /// /***自定义函数*/ pub fn function() {println!("called my::nested::function()"); }#[allow(dead_code)] fn private_function() {println!("called my::nested::private_function()"); }/…...
零代码编程:用ChatGPT批量下载谷歌podcast上的播客音频
谷歌podcast有很多播客音频,如何批量下载到电脑呢? 以这个播客为例: https://podcasts.google.com/feed/aHR0cHM6Ly9oYWRhcnNoZW1lc2guY29tL2ZlZWQvcG9kY2FzdC8?saX&ved0CAkQlvsGahcKEwi4uauWsvKBAxUAAAAAHQAAAAAQAg 查看网页源代码&a…...
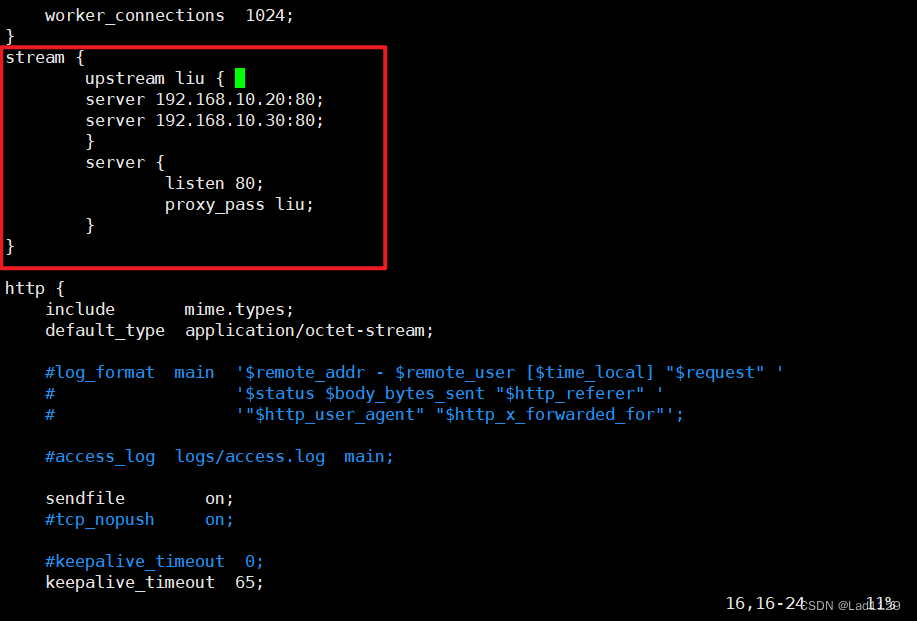
nginx.4——正向代理和反向代理(七层代理和四层代理)
1、正向代理反向代理 nginx当中有两种代理方式 七层代理(http协议) 四层代理(tcp/udp流量转发) 七层代理 七层代理:代理的是http的请求和响应。 客户端请求代理服务器,由代理服务器转发给客户端http请求。转发到内部服务器(可以单台&#…...
基于RuoYi-Flowable-Plus的若依ruoyi-nbcio支持自定义业务表单流程(三)
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 相应的后端也要做一些调整 1、启动流程修改如下: /*** 启动流程实例*/private R startProce…...
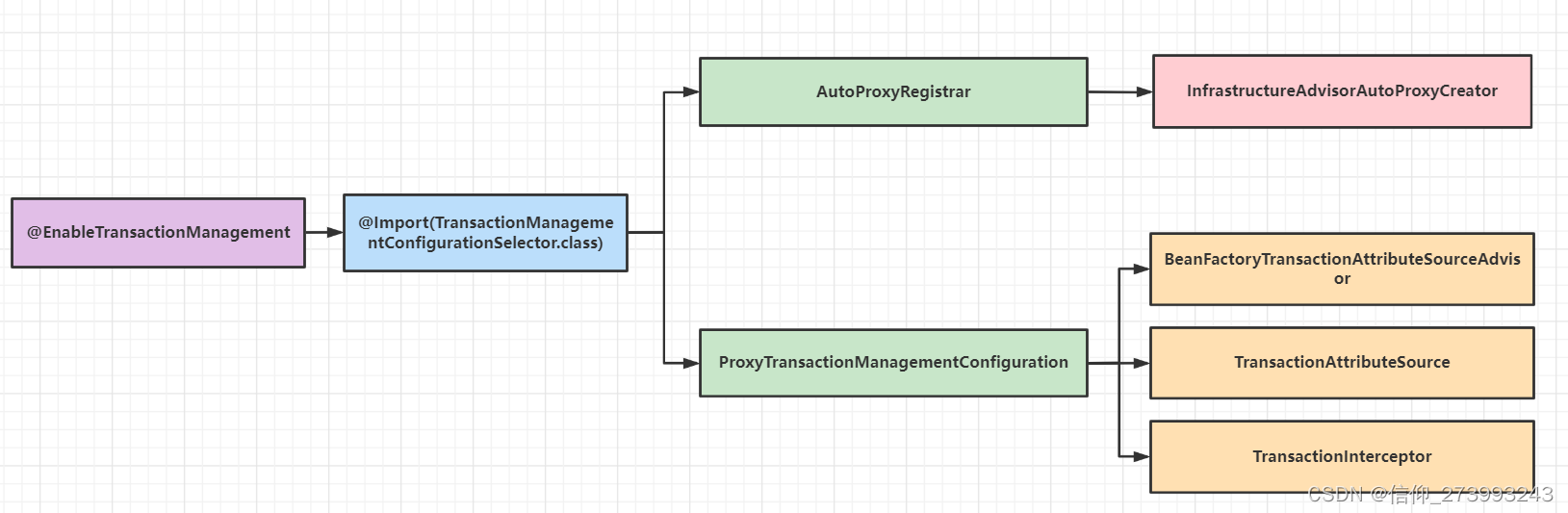
Spring-事务源码解析2
上一篇文章我们介绍了事务开启注解EnableTransactionManagement源码解析《Spring-事务源码解析1》 里面提到了2个关键组件,这里我们分析下Spring如何利用这2个组件来给Bean创建代理对象。 本篇文章我们看下当一个类里面包含了Transactional注解,Spring如…...
基于ssm008医院门诊挂号系统+jsp【附PPT|开题|任务书|万字文档(LW)和搭建文档】
主要功能 后台登录:4个角色 管理员: ①个人中心、修改密码、个人信息 ②药房管理、护士管理、医生管理、病人信息管理、科室信息管理、挂号管理、诊断信息管理、病例库管理、开药信息管理、药品信息管理、收费信息管理 药房: ①个人中心、修…...

【Linux常用命令11】Linux文件与权限详解
权限 r :读权限,用数字4表示 w :写权限,用数字2表示 x :执行权限,用数字1表示 常用权限 644:代表所有者拥有读、写权限,而所属组和其他人拥有只读权限。 755:代表所有…...

BAT026:删除当前目录指定文件夹以外的文件夹
引言:编写批处理程序,实现删除当前目录指定文件夹以外的文件夹。 一、新建Windows批处理文件 参考博客: CSDNhttps://mp.csdn.net/mp_blog/creation/editor/132137544 二、写入批处理代码 1.右键新建的批处理文件,点击【编辑】…...

Python浏览器自动化
如果你正在进行手机爬虫的工作,并且希望通过模拟浏览器行为来抓取数据,那么Pyppeteer将会是你的理想选择。Pyppeteer是一个强大的Python库,它可以让你控制浏览器进行自动化操作,如点击按钮、填写表单等,从而实现数据的…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
