Python每日一练(20230225)

目录
1. 整数反转
2. 求最大公约数和最小公倍数
最大公约数
最小公倍数
3. 单词搜索 II
附录:
DFS 深度优先搜索算法
BFS 广度优先搜索算法
BFS 和 DFS 的区别
1. 整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−2^31, 2^31 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入:x = 123 输出:321
示例 2:
输入:x = -123 输出:-321
示例 3:
输入:x = 120 输出:21
示例 4:
输入:x = 0 输出:0
提示:
-2^31 <= x <= 2^31 - 1
代码:
import math
class Solution:def reverse(self, x: int) -> int:r = 0y = 0abs_x = abs(x)negative = x < 0while abs_x != 0:r = abs_x % 10y = y*10+rabs_x = int(math.floor(abs_x/10))if negative:y = -yreturn 0 if (y > 2147483647 or y < -2147483648) else ys = Solution()
nums = [123, -123, 120, 0, 1234567809]for x in nums:print(s.reverse(x))优化后的代码:
class Solution:def reverse(self, x: int) -> int:num, neg = 0, x<0if neg: x *= -1while x:num = num*10 + x%10x //= 10res = -num if neg else numreturn res if -2**31<=res<2**31 else 0s = Solution()
nums = [123, -123, 120, 0, 1234567809]for x in nums:print(s.reverse(x))代码2: python 数和字串的转换非常方便,负数考虑负号。
class Solution(object):def reverse(self, x:int)->int:res = (-1 if x<0 else 1)*int(str(abs(x))[::-1])return res if -2**31<=res<2**31 else 0s = Solution()
nums = [123, -123, 120, 0, 1234567809]for x in nums:print(s.reverse(x))代码3: 负号还可以用 x//abs(x) 来求,但要排队div by 0。
class Solution(object):def reverse(self, x:int)->int:res = abs(x)//x*int(str(abs(x))[::-1]) if x else 0return res if -2**31<=res<2**31 else 0s = Solution()
nums = [123, -123, 120, 0, 1234567809]for x in nums:print(s.reverse(x))2. 求最大公约数和最小公倍数
输入两个数x 和y,如果x 或y 小于等于0,提示请输入正整数,求这两个数的最大公约数和最小公倍数。
注意:可以采用欧几里得辗转相除算法来求最大公约数。最小公倍数的计算方法是两数的乘积除以两数最大公约数的结果。
x = int(input("输入x:"))
y = int(input("输入y:"))
if x <= 0 or y <= 0:print("请输入正整数")
if x < y:x,y = y,x
v1 = x*y
v2 = x%y
while v2 != 0:x = yy = v2v2 = x % y
v1 =v1 // y
print("最大公约数为:%d" % y)
print("最小公倍数为:%d" % v1) 最大公约数
方法一:for循环
def GCD(m, n):gcd = 1 # 此行可以省略for i in range(1,min(m, n)+1):if m%i==0 and n%i==0:gcd = ireturn gcdprint(GCD(81,3))print(GCD(81,15))print(GCD(81,54))方法二:while循环
def GCD(m, n):while m!=n:if m>n: m -= nelse: n -= mreturn mprint(GCD(81,3))print(GCD(81,15))print(GCD(81,54))方法三:递归法
def GCD(m, n):if n==0: return mreturn GCD(n, m%n)print(GCD(81,3))print(GCD(81,15))print(GCD(81,54))方法四:辗转相除法
def GCD(m, n):while n!=0:m, n = n, m%nreturn mprint(GCD(81,3))print(GCD(81,15))print(GCD(81,54))方法五:递减法
def GCD(m, n):gcd = min(m, n)while m%gcd or n%gcd:gcd -= 1return gcdprint(GCD(81,3))print(GCD(81,15))print(GCD(81,54))方法六:库函数math.gcd
from math import gcdprint(gcd(81,3))print(gcd(81,15))print(gcd(81,54))或者:直接用 __import__('math').gcd
__import__('math').gcd(81,3)
__import__('math').gcd(81,15)
__import__('math').gcd(81,54)方法七:约分法,库函数fractions.Fraction()
def GCD(m, n):from fractions import Fractionreturn m//Fraction(m, n).numerator #取分子#return n//Fraction(m, n).denominator #或取分母print(GCD(81,3))print(GCD(81,15))print(GCD(81,54))最小公倍数
方法一:循环暴力法
def LCM(m, n):for i in range(max(m,n),m*n+1):if i%m==0 and i%n==0:return iprint(LCM(81,3))print(LCM(81,15))print(LCM(81,54))方法二:与最大公约数的关系
最小公倍数LCM 与 最大公约数GCD的关系: m * n = LCM(m, n) * GCD(m, n)
对应最大公约数的几种方法,返回 m*n 整除 GCD(m,n) 即可。
3. 单词搜索 II
给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words,找出所有同时在二维网格和字典中出现的单词。
单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
示例 1:
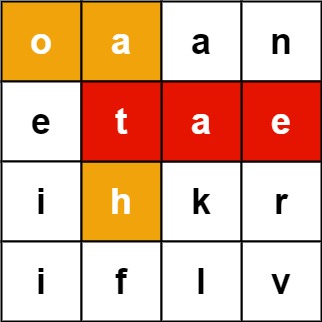
输入:board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"] 输出:["eat","oath"]
示例 2:
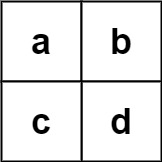
输入:board = [["a","b"],["c","d"]], words = ["abcb"] 输出:[]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 12board[i][j]是一个小写英文字母1 <= words.length <= 3 * 1041 <= words[i].length <= 10words[i]由小写英文字母组成words中的所有字符串互不相同
class Solution:def findWords(self, board: list, words: list) -> list:if not board or not board[0] or not words:return []self.root = {}for word in words:node = self.rootfor char in word:if char not in node:node[char] = {}node = node[char]node["#"] = wordres = []for i in range(len(board)):for j in range(len(board[0])):tmp_state = []self.dfs(i, j, board, tmp_state, self.root, res)return resdef dfs(self, i, j, board, tmp_state, node, res):if "#" in node and node["#"] not in res:res.append(node["#"])if [i, j] not in tmp_state and board[i][j] in node:tmp = tmp_state + [[i, j]]candidate = []if i - 1 >= 0:candidate.append([i - 1, j])if i + 1 < len(board):candidate.append([i + 1, j])if j - 1 >= 0:candidate.append([i, j - 1])if j + 1 < len(board[0]):candidate.append([i, j + 1])node = node[board[i][j]]if "#" in node and node["#"] not in res:res.append(node["#"])for item in candidate:self.dfs(item[0], item[1], board, tmp, node, res)if __name__ == '__main__':s = Solution()board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]]words = ["oath","pea","eat","rain"]print(s.findWords(board, words))board = [["a","b"],["c","d"]]words = ["abcb"]print(s.findWords(board, words))
输出:
['oath', 'eat']
[]
附录:
DFS 深度优先搜索算法
Depth-First-Search,是一种用于遍历或搜索树或图的算法。这个算法会尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
BFS 广度优先搜索算法
Breadth-First Search,又译作宽度优先搜索,或横向优先搜索,是一种图形搜索算法。简单的说,BFS是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。
BFS 和 DFS 的区别
1 数据结构
bfs 遍历节点是先进先出,一般使用队列作为辅助数据结构
dfs遍历节点是先进后出,一般使用栈作为辅助数据结构
2 访问节点的方式
bfs是按层次访问的,先访问源点,再访问它的所有相邻节点,并且标记结点已访问,根据每个邻居结点的访问顺序,依次访问它们的邻居结点,并且标记节点已访问,重复这个过程,一直访问到目标节点或无未访问的节点为止。
dfs 是按照一个路径一直访问到底,当前节点没有未访问的邻居节点时,然后回溯到上一个节点,不断的尝试,直到访问到目标节点或所有节点都已访问。
3 应用
bfs 适用于求源点与目标节点距离近的情况,例如:求最短路径。
dfs 更适合于求解一个任意符合方案中的一个或者遍历所有情况,例如:全排列、拓扑排序、求到达某一点的任意一条路径。
相关文章:

Python每日一练(20230225)
目录 1. 整数反转 2. 求最大公约数和最小公倍数 最大公约数 最小公倍数 3. 单词搜索 II 附录: DFS 深度优先搜索算法 BFS 广度优先搜索算法 BFS 和 DFS 的区别 1. 整数反转 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。…...
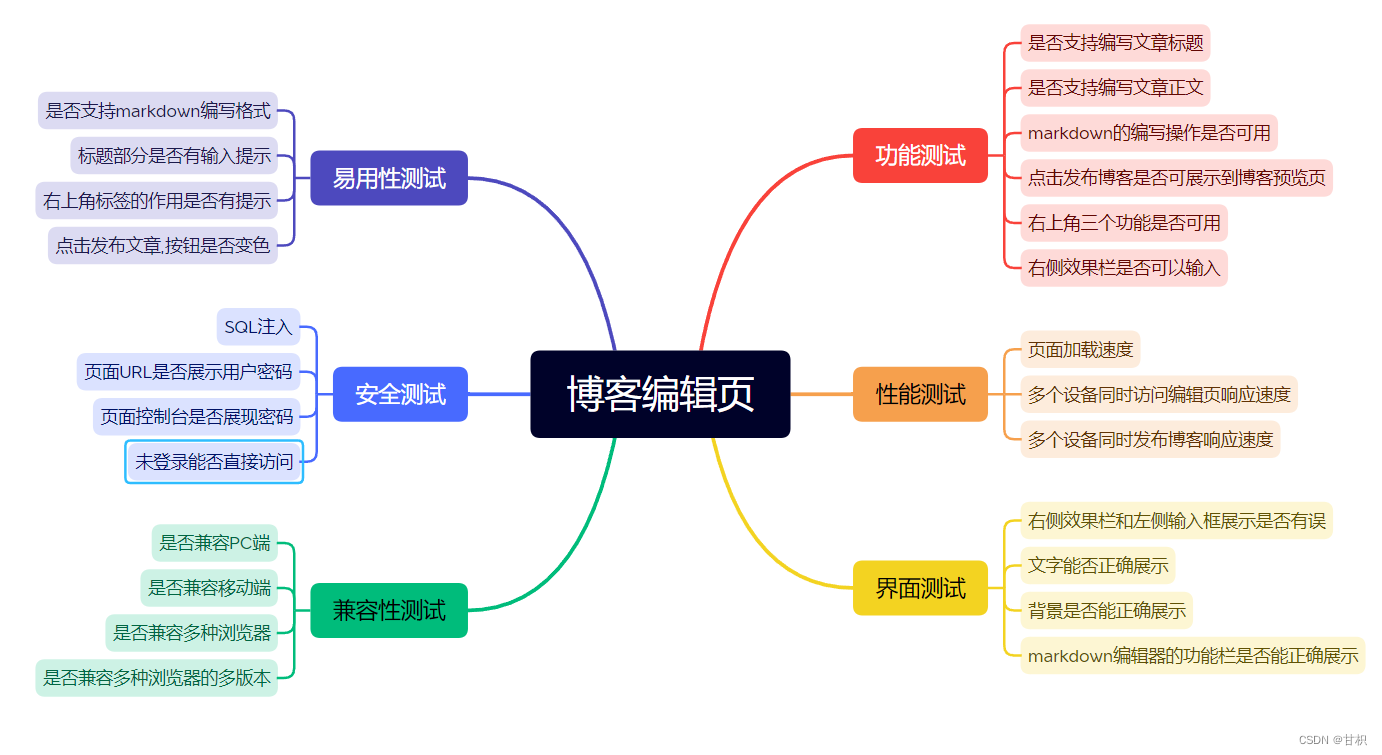
基于博客系统的测试用例
登陆界面博客预览页博客详情页博客编辑页...

C语言运算符算术运算符关系运算符
C 运算符 运算符是一种告诉编译器执行特定的数学或逻辑操作的符号。C 语言内置了丰富的运算符,并提供了以下类型的运算符: 算术运算符 关系运算符 逻辑运算符 位运算符 赋值运算符 杂项运算符 本章将逐一介绍算术运算符、关系运算符、逻辑运算符、位运…...

C语言 深度剖析数据在内存中的存储
目录数据类型详细介绍整形在内存中的存储:原码,反码,补码大小端字节序介绍及判断浮点型在内存中的存储解析数据类型详细介绍整形:1.为什么char类型也会归类到整形家族当中去呢?字符存储和表示的时候本质上使用的是ASCI…...

MyBatis快速开发
查询user表中的所有数据 步骤: 创建user表 打开Navicat,新建查询,将下面SQL代码复制粘贴并执行: create database mybatis; use mybatis;drop table if exists tb_user;create table tb_user(id int primary key auto_incremen…...
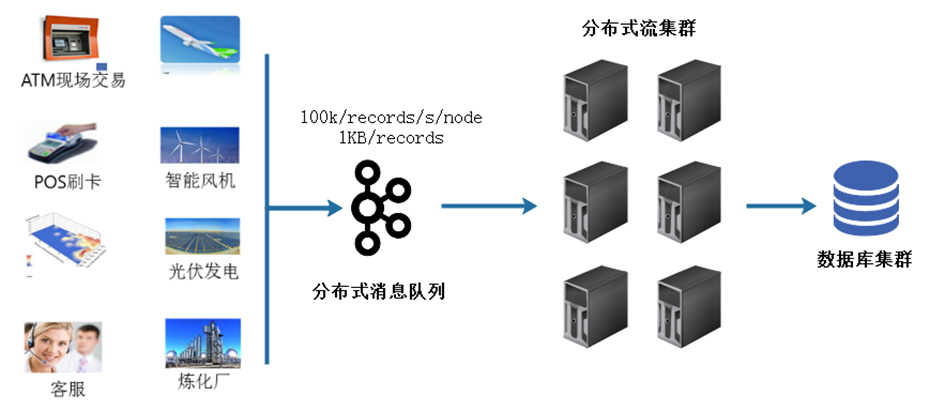
大数据常见应用场景及架构改进
大数据常见应用场景及架构改进大数据典型的离线处理场景1.大数据数据仓库及它的架构改进2.海量数据规模下的搜索与检索3.新兴的图计算领域4.海量数据挖掘潜在价值大数据实时处理场景大数据典型的离线处理场景 1.大数据数据仓库及它的架构改进 对于离线场景,最典型…...

【华为OD机试模拟题】用 C++ 实现 - 挑选字符串(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 货币单位换算(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 选座位(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 停车场最大距离(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 重组字符串(2023.Q1) 【华为OD机试模…...
程序员是世界上最理性、最睿智的群体,耶稣也反驳不了我,我说的!
有人说,程序员是吃青春饭的,35 岁就提前退休了。 猛一看,这句话是对的;仔细一看,这句话是不对的。 说它对,是因为现实中确实有很多程序员 35 岁就被毕业了;说它不对,是因为 35 岁以…...

人工智能到底是什么?
人工智能(Artificial Intelligence,AI)是一种利用计算机科学和统计学理论和技术来实现人类智能的一门交叉学科,旨在使计算机系统能够模拟、扩展和增强人类的智能能力,使计算机能够像人类一样思考、学习、决策和执行任务…...
)
在动态规划的海洋中遨游(三)
前言:\textcolor{Green}{前言:}前言: 💞 好久没写题,有点生疏了。这也是给大家提一个醒,一定要一直坚持下去,哪怕每天只做一点点。💞 算法类别一、算法介绍原理适用的情况做题步骤二…...

enable_if模板编程实现字节序转换模板
enable_if和SFINAESFINAE是模板的一个特性,也就是替换失败不报错。正常来说,函数匹配的时候按照优先级依次匹配定义的重载函数,最终选择最佳匹配的函数运行。模板也是一样的,但是在替换模板时,即使出现异常错误也不认为…...

【人工智能与深度学习】基于能量的模型
【人工智能与深度学习】基于能量的模型 概述能量基础模型(EBM)方法定义解决方案:基于梯度的推理有潜在变量的能量基础模型推理例子能量基础模型和机率模型的对比自由能(Free Energy)概述 我们现在介绍一个新框架来定义模型。它提供了一个统一和系列性的方式来定义「监督模型」…...
功能测试三年,是应该改变了
前言 测试行业3年多经验,学历大专自考本科,主要测试方向web,PC端,wap站,小程序公众号都测试过,app也测过一些,C端B端都有,除功能外,接口性能也有涉猎,但是不…...
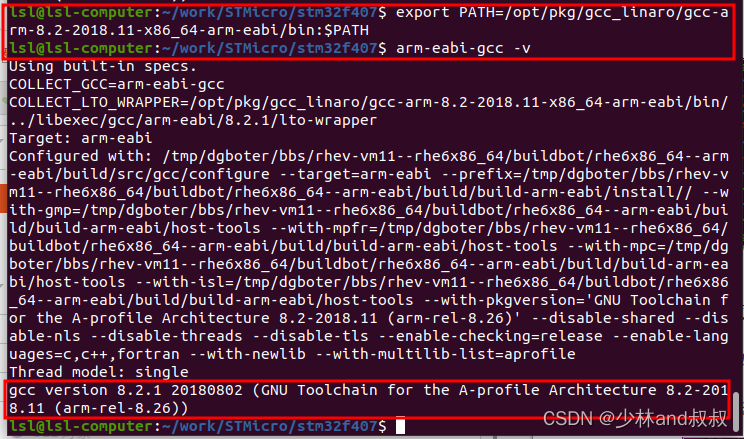
基于STM32的ubuntu交叉编译环境的搭建(arm-gcc 8.2)
常用的STM32的软件开发方法都是基于MDK keil或IAR集成开发环境,但以上两个集成开发环境软件都是需要收费的,且价格较为昂贵。本节介绍一种在ubuntu上安装arm gcc(arm-eabi)的方式,用于编译STM32的程序。 1.在arm官网下…...

数据结构:二叉树概念篇(算法基础)
目录 一.有向树的图论基础 1.有向树的相关基本概念 有向树的基本定义: 有向树的结点的度: 有向树的度: 有向树的根结点,分枝结点,叶结点: 树的子树: 树结点的层次: 树的高度: 2.一个基本的数学结论 3.有序有向树 二.数据结构中树的顺序存储结构与链式存…...

华为OD机试真题Java实现【字符串变换最小字符串】真题+解题思路+代码(20222
字符串变换最小字符串 给定一个字符串s,最多只能进行一次变换,返回变换后能得到的最小字符串(按照字典序进行比较)。 变换规则:交换字符串中任意两个不同位置的字符。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Java)真题目录汇总 ## 输入输出描述: …...

数字化转型的企业会用低代码平台深化重塑什么形态
随着数字化转型的浪潮不断推进,越来越多的企业开始关注如何更好地利用数字技术提高业务效率和创新能力。而低代码平台作为一种能够快速构建和部署应用程序的新型工具,正越来越受到企业的青睐。那么,数字化转型的企业会用低代码平台深化重塑什…...

【华为OD机试模拟题】用 C++ 实现 - 拼接 URL(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

六千字让你明白什么是数字孪生?
文章目录1. 背景2. 数字孪生基础2.1 概念2.2 价值3. 技术生态3.1 技术体系3.2 核心技术3.2.1 多领域、多尺度融合建模3.2.2 数据驱动与物理模型融合的状态评估3.2.3 数据采集和传输3.2.4 全生命周期数据管理3.2.5 虚拟现实呈现3.2.6 高性能计算3.3 建设3.3.1 重点3.3.1.1 数字孪…...
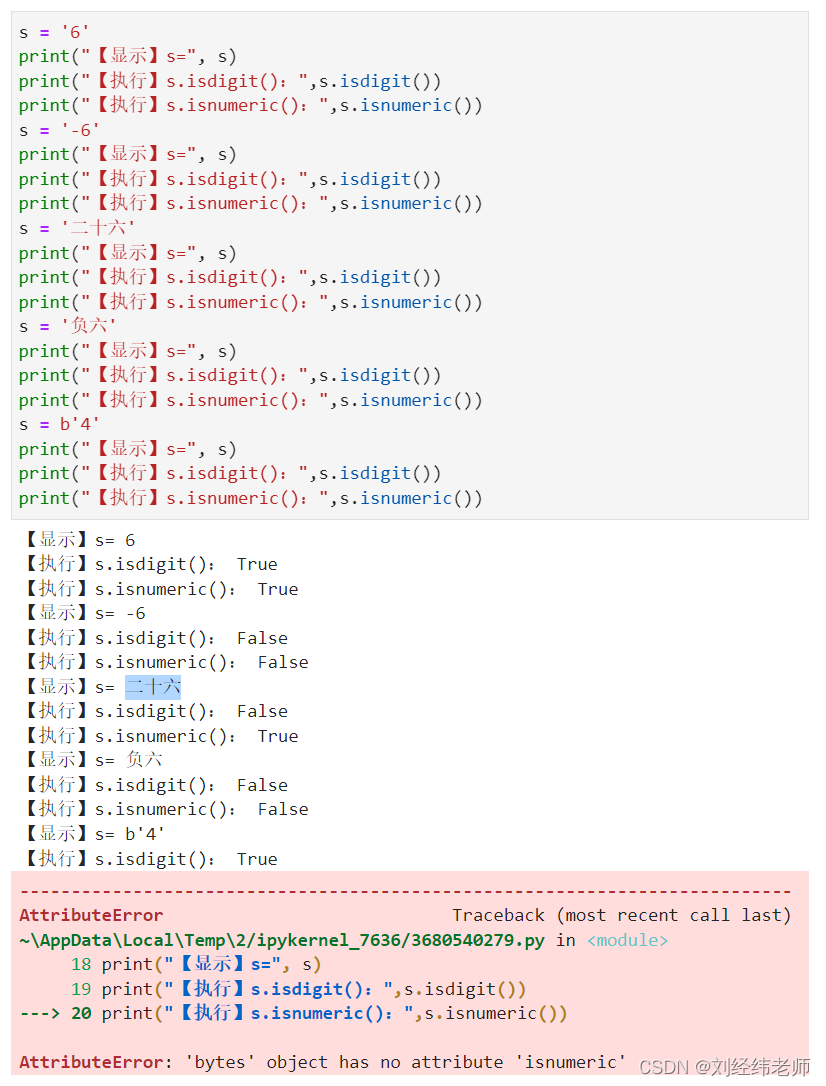
判断字符串是否是纯数字不包括符号(含符号显示False)isnumeric()和isdigit()
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 判断字符串是否是纯数字 不包括符号(含符号显示False) isnumeric()和isdigit() [太阳]选择题 对于代码中当s为‘二十六’时isdigit()和isnumeric()输出的结果是? s …...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
