【数据存储:小端模式和大端模式】
一、引言
在计算机科学中,数据存储模式是指如何将数据存储在计算机内存中的方式。小端模式和大端模式是两种主要的字节序方式,它们决定了字节在内存中的排列顺序。这种字节顺序的选择对于跨平台编程和数据传输至关重要。在这篇博客中,我们将详细介绍小端模式和大端模式,并通过图解的方式帮助你更好地理解这两种数据存储方式。
二、小端模式(Little-endian)
小端模式是一种将高字节存储在低地址处,将低字节存储在高地址处的字节序方式。在这种模式下,内存地址从低到高依次存储了多字节值的各个字节,即低地址处存储了数值的低位,高地址处存储了数值的高位。这种方式在许多现代计算机中都被广泛采用。
小端模式:
- 假设我们有一个8字节的数据(如整数或浮点数),从左到右依次为字节1、字节2、字节3、字节4、字节5、字节6、字节7和字节8。
- 在小端模式中,字节1存储在最低的内存地址处,字节8存储在最高的内存地址处。
- 读取数据时,从最低地址开始读取,依次读取每个字节,得到的结果就是原数据的反码形式(因为在内存中,最高位是物理地址的最高位)。
举个小栗子:
如果将一个 32位的整数 0x12345678 存放到一个整型变量(int)中,这个整型变量采用小端模式在内存中的存储由下表所示。
为简单起见,本文使用 OP0 表示一个 32位数据的最高字节 MSB(Most Significant Byte),使用 OP3 表示一个 32位数据最低字节 LSB(Least Significant Byte)。
| 地址偏移 | 小端模式 |
|---|---|
| 0x00 | 78(OP3) |
| 0x01 | 56(OP2) |
| 0x02 | 34(OP1) |
| 0x03 | 12(OP0) |
三、大端模式(Big-endian)
大端模式则恰恰相反,它把低字节存储在内存的高地址处,把高字节存储在内存的低地址处。在这种模式下,高地址处存储的是数值的低位,低地址处存储的是数值的高位。在一些古老的计算机体系中,大端模式被采用。
大端模式:
- 同样以一个8字节的数据为例,从左到右依次为字节1、字节2、字节3、字节4、字节5、字节6、字节7和字节8。
- 在大端模式中,字节8存储在最低的内存地址处,字节1存储在最高的内存地址处。
- 读取数据时,从最高地址开始读取,依次读取每个字节,得到的结果就是原数据的原码形式。
举个小栗子:
如果将一个 32位的整数 0x12345678 存放到一个整型变量(int)中,这个整型变量采用大端模式在内存中的存储由下表所示。
为简单起见,本文使用 OP0 表示一个 32位数据的最高字节 MSB(Most Significant Byte),使用 OP3 表示一个 32位数据最低字节 LSB(Least Significant Byte)。
| 地址偏移 | 大端模式 |
|---|---|
| 0x00 | 12(OP0) |
| 0x01 | 34(OP1) |
| 0x02 | 56(OP2) |
| 0x03 | 78(OP3) |
四、选择小端模式的原因
尽管大端模式在一些早期的计算机体系中很常见,但在现代计算机系统中,小端模式更常见,因为它在不同的系统和架构中表现得更好。小端模式的优点在于它可以更好地处理跨平台的数据传输,因为无论系统架构如何变化,数据的字节顺序都是一致的。此外,由于现代计算机系统通常使用小端模式,因此大多数编程语言(如C/C++)都默认使用小端模式进行数据存储。
五、结论
总之,小端模式和大端模式是两种不同的数据存储方式,它们的选择取决于不同的系统架构和需求。在现代计算机系统中,小端模式更为常见,因为它在各种不同的系统和架构中表现得更好。了解这两种模式对于跨平台编程和数据传输至关重要。
相关文章:

【数据存储:小端模式和大端模式】
一、引言 在计算机科学中,数据存储模式是指如何将数据存储在计算机内存中的方式。小端模式和大端模式是两种主要的字节序方式,它们决定了字节在内存中的排列顺序。这种字节顺序的选择对于跨平台编程和数据传输至关重要。在这篇博客中,我们将…...

【git】gitlab安装、备份
gitlab官网 官网:官网 中文官网:中文官网 作为一个英文不好的程序员,所以我都去中文网站去看了。下面也是带着大家去走走 安装gitlab 我不想写具体的安装方法,直接去逛网看下面是我的截图。步骤非常详细。 安装文档地址&…...
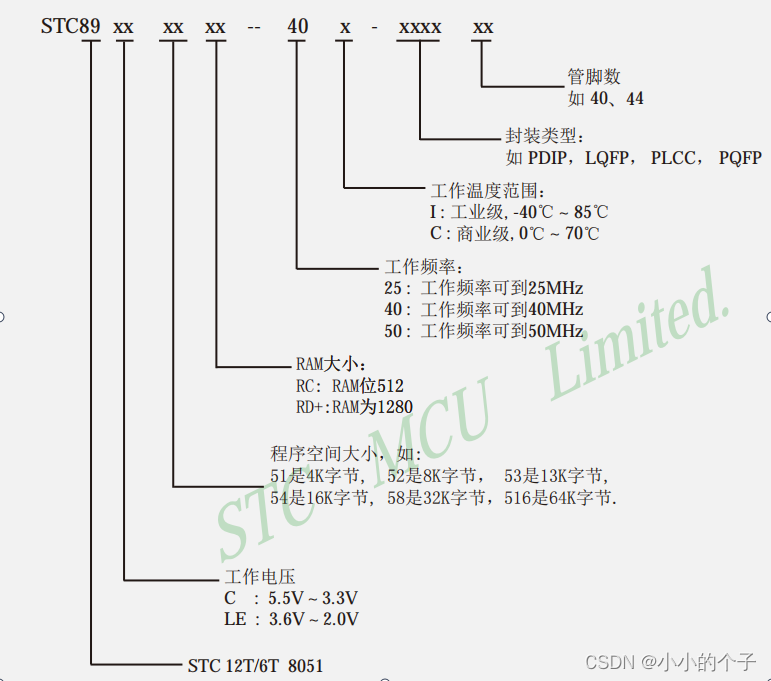
C51--基本认知
单片机基本认知: 1、什么是单片机 单片机是一种集成电路芯片。 把具有数据处理能力的中央处理器 CPU、随机存储器RAM、只读存储器ROM。 多种 I / O 口和中断系统、定时器/计数器等功能(可能还包括显示驱动电路、脉宽调制电路、模拟多路转换器、A/D转换器…...
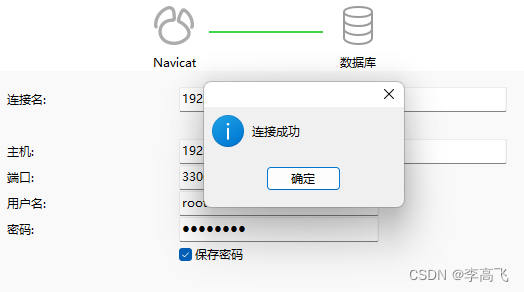
centos7 安装 mysql 8.0
文章目录 环境介绍一、安装前准备 1.卸载MariaDB 1.1 查看是否安装mariadb1.2 卸载1.3 检查是否卸载干净 2.检查依赖 2.1 查看是否安装libaio2.2 查看是否安装numactl 二、安装MySQL 1.下载资源包 1.1 官网下载1.2 wget下载 2.解压3.重命名4.创建存储数据文件5.设置用户组并赋…...
)
Vue15 计算属性VS监视属性(侦听属性)
计算属性VS监视属性(侦听属性) computed和watch之间的区别: 1.computed能完成的功能,watch都可以完成。 2.watch能完成的功能,computed不一定能完成,例如:watch可以进行异步操作。 两个重要的小…...

快速全面掌握数据库系统核心知识点
快速全面掌握数据库系统核心知识点 一、数据库系统二、三级模式-两层映射三、三级模式-视图四、数据库设计过程五、E-R模型六、关系代数七、规范化理论八、函数依赖九、规范化理论-键十、规范化理论-求候选键十一、规范化理论-范式十二、规范化理论-第一范式十三、规范化理论-第…...

学习笔记 | 音视频 | 推流项目框架及细节
推流项目: 跑起来项目,再调,创造问题,注意项目跑起来包括哪些步骤 前期准备:环境的配置 依赖库要交叉编译,编译还需注意依赖的库对应的头文件(注意是绝对路径还是相对路径) Rv1126_lib、arm_libx264、arm_libx265、arm_libsrt、arm32_ffmpeg_srt、arm_openssl Ubuntu搭…...
拓扑几何学
目录 一,欧拉定理 1,平面图论图 2,单连通多面体 3,一般多面体 一,欧拉定理 1,平面图论图 在一个联通无向图中,点数-边数面数 1 如: 7-126 1 如果把最外面的五边形外面也算…...

1.12.C++项目:仿muduo库实现并发服务器之LoopThreadPool模块的设计
文章目录 一、LoopThreadPool模块二、实现思想(一)功能(二)意义(三)功能设计 三、代码 一、LoopThreadPool模块 1.线程数量可配置(0或多个) 2. 对所有的线程进行管理,其…...

SpringBoot介绍
一、什么是SpringBoot 在使用传统的Spring去做Java EE(Java Enterprise Edition)开发中,大量的 XML 文件存在于项目之中,导致JavaEE项目变得慢慢笨重起来,繁琐的配置和整合第三方框架的配置,导致了开发和部…...

2022最新版-李宏毅机器学习深度学习课程-P17 卷积神经网络CNN
一、CNN 用于图像分类 需要图片大小统一 彩色图像分为R G B 三层,展平后首尾相接 值代表着颜色的强度 图像识别中不需要全连接的,参数太多了 观测1:通过判断多个小局部图像就能判断出图片标签 感受野的定义 简化1 感受野可以重叠ÿ…...

微博清理僵尸粉
1.选择chrome或者firefox浏览器 2.登陆微博账号 3.chrome右键点检查,选择console firefox右键点检查,选择控制台 4.粘贴下面代码到console或者控制台并且回车 let removeTargetFans false; /*是否删除符合条件的粉丝,默认关闭*/let dee…...

创建React Native的第一个hello world工程
创建React Native的第一个hello world工程 需要安装好node、npm环境 如果之前没有安装过react-native-cli脚手架的,可以按照下述步骤直接安装。如果已经安装过的,但是在使用这个脚手架初始化工程的时候遇到下述报错的话 cli.init(root, projectname);…...
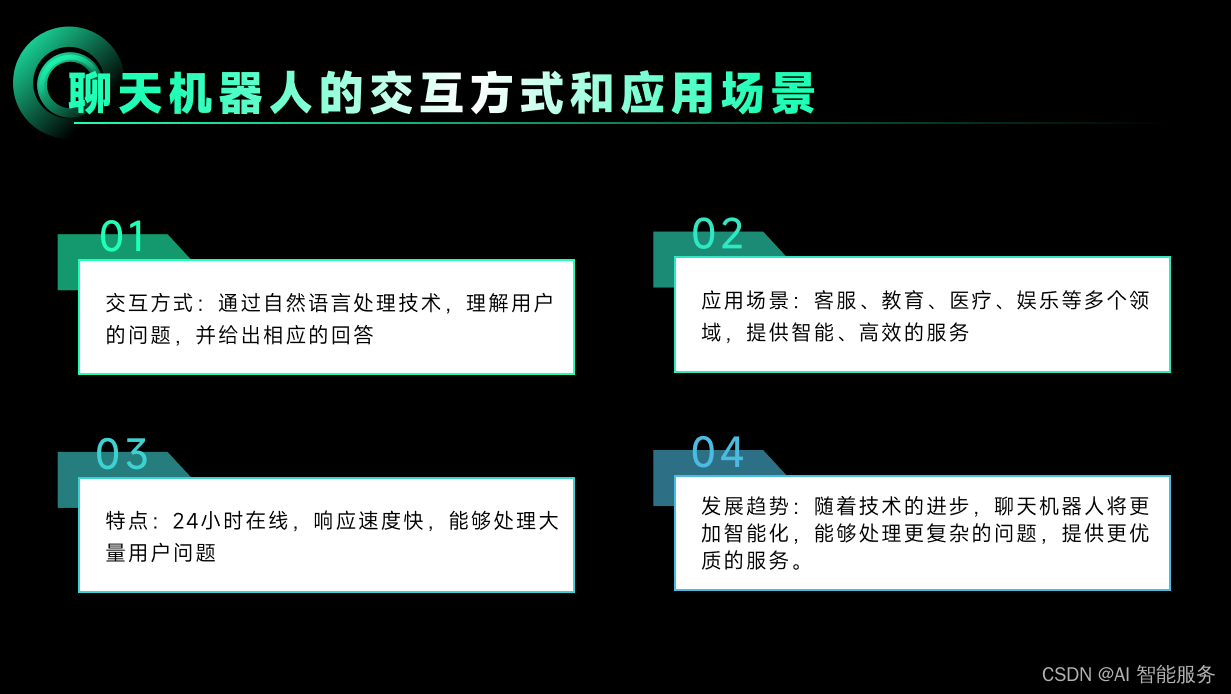
基础课3——自然语言处理的应用
自然语言处理是一种将人类语言转换为机器语言,以实现人机交互的技术。应用非常广泛,例如: 人机交互:自然语言处理技术可以应用于人机交互,让机器能够理解和运用人类语言,从而实现更加智能化的交互体验。 机…...
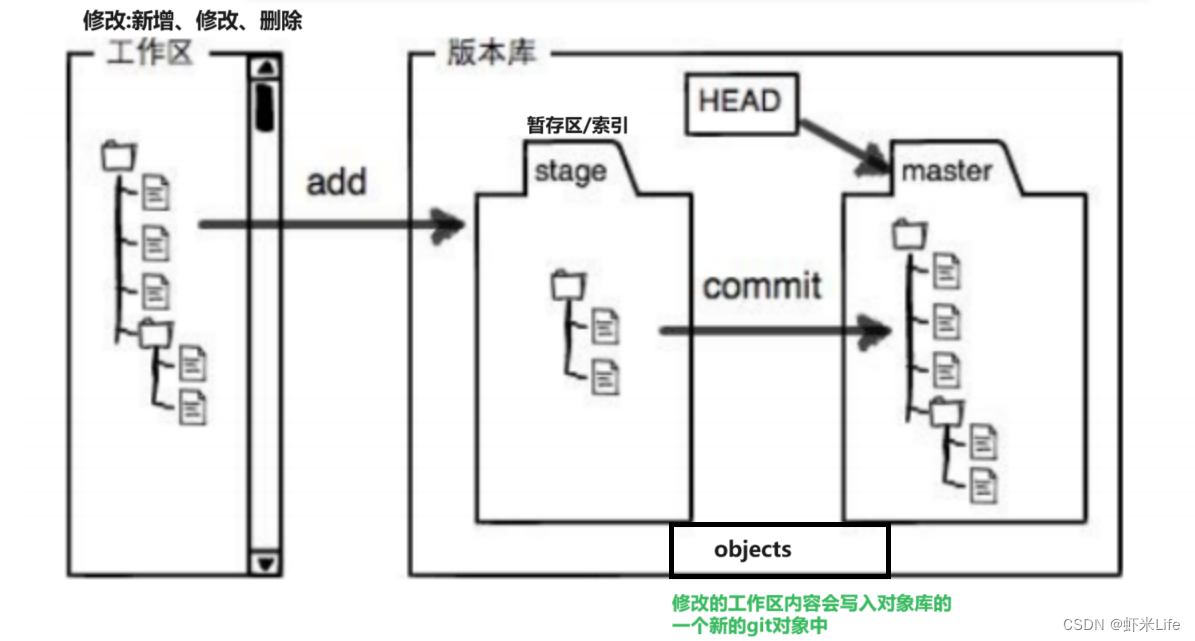
理解 Git 的三个工作区:工作区、暂存区和版本库
文章目录 创建 Git 本地仓库配置Git认识⼯作区、暂存区、版本库添加⽂件--场景查看 .git ⽂件添加⽂件--场景⼆ 创建 Git 本地仓库 要提前说的是,仓库是进⾏版本控制的⼀个⽂件⽬录。我们要想对⽂件进⾏版本控制,就必须先创建⼀个仓库出来。创建⼀个 Gi…...

web前端基础训练-----创建用户反馈表单
1,实验代码 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>用户反馈表单</title></head><body><form><fieldset><h1>用户反馈</h1><hr/><h4>亲爱的用…...

Scrum 敏捷管理流程图及敏捷管理工具
敏捷开发中的Scrum流程通常可以用一个简单的流程图来表示,以便更清晰地展示Scrum框架的各个阶段和活动。以下是一个常见的Scrum流程图示例: 转自:Leangoo.com 免费敏捷工具 这个流程图涵盖了Scrum框架的主要阶段和活动,其中包括…...

Android Handler/Looper视角看UI线程的原理
概述 Handler/Looper机制是android系统非重要且基础的机制,即使在rtos或者linux操作系统上开发应用框架时,也经常借鉴这个机制。通过该机制机制可以让一个线程循环处理事件,事件处理逻辑即在Handler的handleMessge种。本文建议android8.1源码…...
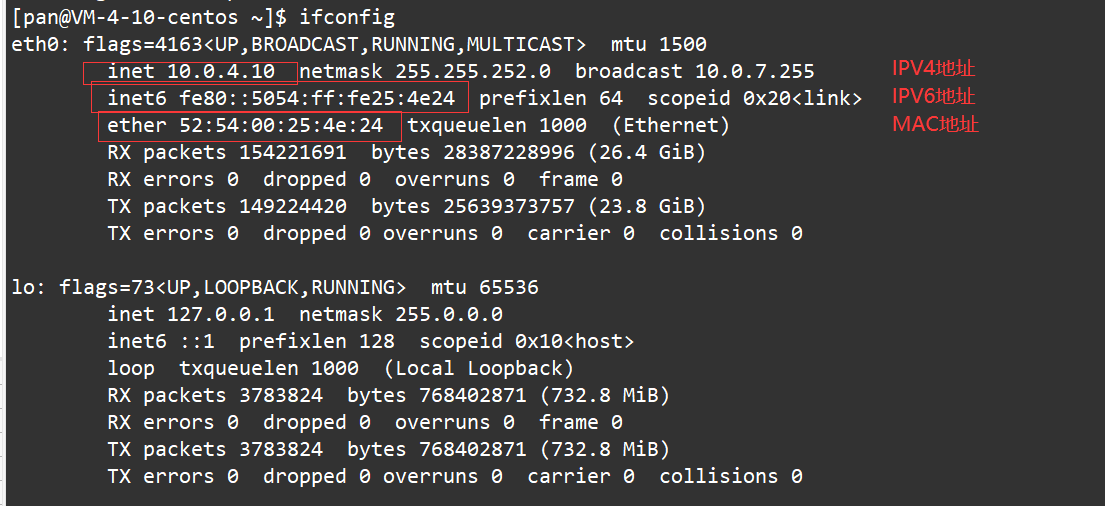
【网络】网络入门
网络入门 一、网络发展二、网络协议初识1、认识"协议"2、协议分层3、OSI七层模型4、TCP/IP五层(或四层)模型 三、网络传输基本流程1、同局域网的两台主机通信2、跨网络的两台主机通信 四、网络中的地址管理1、IP地址2、认识MAC地址 一、网络发展 独立模式:…...

GO-实现简单文本格式 文本字体颜色、大小、突出
毫无疑问GO的生态就是一坨大便。老子英文水平小学啊。 实现简单文本格式 文本字体颜色、大小、突出显示等。 创建要给docx文件容器【我估算的】 doc : document.New() defer doc.Close() doc.SaveToFile("simple.docx") 把容器保存为文件 设置标题 创建自然段…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
