企业如何通过媒体宣传扩大自身影响力
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。
企业可以通过媒体宣传来扩大自身的影响力。可以通过以下的方法。

1. 制定媒体宣传战略:
- 首先,制定一份清晰的媒体宣传战略,明确您的宣传目标、目标受众以及核心信息。
2. 媒体关系建设:
- 建立和维护良好的媒体关系,包括与记者、编辑和主编的沟通。这可以通过参加行业活动、举办媒体见面会、提供有价值的信息和故事来实现。
3. 新闻稿发布:
- 撰写和发布新闻稿,宣传企业的重要事件、新产品、合作伙伴关系或任何其他有新闻价值的信息。确保新闻稿质量高,具备吸引力,以便媒体愿意报道。
4. 社交媒体:
- 利用社交媒体平台扩大企业的声誉和影响力。分享有趣的内容,与受众互动,并使用相关标签和关键字以增加可见性。
5. 内容营销:
- 创建有吸引力的内容,如博客文章、白皮书、研究报告和视频,以展示您在行业中的专业知识。将这些内容分享到您的网站和社交媒体上,以吸引更多受众。
6. 危机管理:
- 准备好危机管理计划,以应对负面媒体报道或突发事件。及时回应问题,积极沟通,维护企业声誉。
7. 赞助和合作:
- 考虑赞助重要行业活动、项目或慈善事业,以提高企业知名度。与其他企业、组织或个人建立合作关系,以共同宣传和推广。
8.搜索引擎优化 (SEO):
- 通过优化您的网站和在线内容,提高在搜索引擎结果中的排名,以吸引更多的有机流量。
9. 使用多种媒体渠道:
- 利用不同类型的媒体,包括印刷媒体、广播、电视、在线媒体和社交媒体,以覆盖更广泛的受众。
10.度量和分析:
- 使用分析工具来追踪媒体宣传活动的效果。了解哪些策略和渠道最有效,以便进行必要的调整和改进。
媒体宣传是建立和维护企业形象的重要工具,但需要计划和执行,确保信息准确、一致,同时满足目标受众的需求。
相关文章:

企业如何通过媒体宣传扩大自身影响力
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 企业可以通过媒体宣传来扩大自身的影响力。可以通过以下的方法。 1. 制定媒体宣传战略: - 首先,制定一份清晰的媒体宣传战略,明确您的宣传目标、目标…...

处理vue直接引入图片地址时显示不出来的问题 src=“[object Module]“
在webpack中使用vue-loader编译template之后,发现图片加载不出来了,开发人员工具中显示src“[object Module]” 这是因为当vue-loader编译template块之后,会将所有的资源url转换为webpack模块请求 这是因为vue使用的是commonjs语法规范&…...
vue3 v-md-editor markdown编辑器(VMdEditor)和预览组件(VMdPreview )的使用
vue3 v-md-editor markdown编辑器和预览组件的使用 概述安装支持vue3版本使用1.使用markdown编辑器 VMdEditor2.markdown文本格式前端渲染 VMdPreview 例子效果代码部分 完整代码 概述 v-md-editor 是基于 Vue 开发的 markdown 编辑器组件 轻量版编辑器 轻量版编辑器左侧编辑…...

java正则表达式 及应用场景爬虫,捕获分组非捕获分组
正则表达式 通常用于校验 比如说qq号 看输入的是否符合规则就可以用这个 public class regex {public static void main(String[] args) {//正则表达式判断qq号是否正确//规则 6位及20位以内 0不能再开头 必须全是数子String qq"1234567890";System.out.println(qq…...

基于 Debian 稳定分支发行版的Zephix 7 发布
Zephix 是一个基于 Debian 稳定版的实时 Linux 操作系统。它可以完全从可移动媒介上运行,而不触及用户系统磁盘上存储的任何文件。 Zephix 是一个基于 Debian 稳定版的实时 Linux 操作系统。它可以完全从可移动媒介上运行,而不触及用户系统磁盘上存储的…...
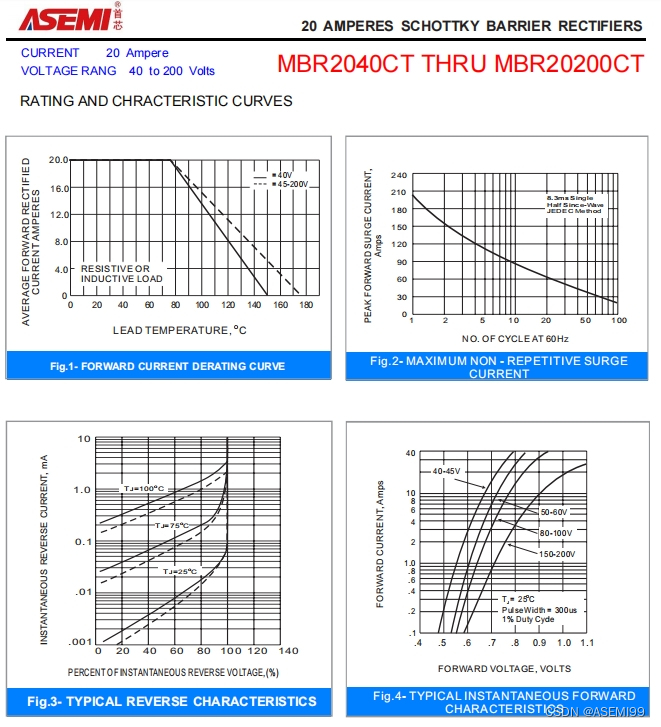
MBR20100CT-ASEMI肖特基MBR20100CT参数、规格、尺寸
编辑:ll MBR20100CT-ASEMI肖特基MBR20100CT参数、规格、尺寸 型号:MBR20100CT 品牌:ASEMI 芯片个数:2 封装:TO-220 恢复时间:>50ns 工作温度:-65C~175C 浪涌电流:…...
修炼k8s+flink+hdfs+dlink(五:安装dockers,cri-docker,harbor仓库)
一:安装docker。(所有服务器都要安装) 安装必要的一些系统工具 sudo yum install -y yum-utils device-mapper-persistent-data lvm2添加软件源信息 sudo yum-config-manager --add-repo https://mirrors.aliyun.com/docker-ce/linux/cent…...
github: kex_exchange_identification: Connection closed by remote host
问题描述 (base) ➜ test git:(dev) git pull kex_exchange_identification: Connection closed by remote host Connection closed by 192.30.255.113 port 22 致命错误:无法读取远程仓库。解决方案 参照下边文档 https://docs.github.com/en/authentication/tr…...

AWS香港Web3方案日,防御云安全实践案例受关注
9月26日,AWS合作伙伴之Web3解决方案日在香港举办。来自人工智能、Web3等领域的创业公司、技术专家、风险投资商,就元宇宙时代未来发展进行了深入交流。现场展示了顶象防御云在金融与Web3领域的安全实践案例。 Web3为互联网体系架构的一个整体演进和升级&…...

QT 集成MQTT过程
1 编译库文件 Qt QtMqtt官方源码编译教程_“qtmqtt/qmqttglobal.h”: no such file or directory-CSDN博客 2 参考文献 Qt开发MQTT(一) 之Qt官方Qt MQTT-CSDN博客 QTMQTT 使用MQTT官方库_qt mqtt 官方库-CSDN博客...
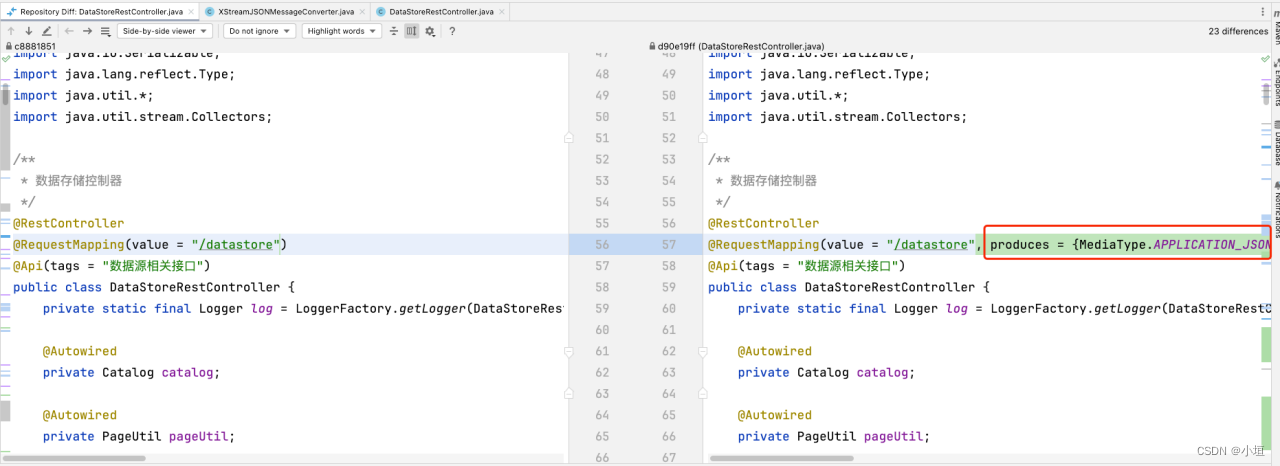
GeoServer改造Springboot启动五(解决接口返回xml而不是json)
请求接口返回的是xml,而不是我们常用的json,问题呈现如下图 40 图 40请求接口返回XML 在RequestMapping注解上增加produces {MediaType.APPLICATION_JSON_UTF8_VALUE} 图 41增加produces...
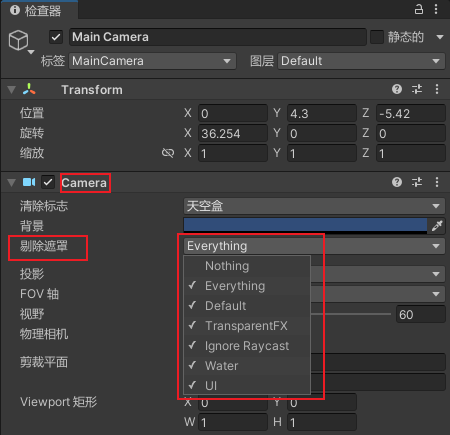
在unity中给游戏物体一个标记
标记 方便识别! 标签(Tag) 引擎内部会对物体的标签建立了索引。通过标签查找物体,要比通过名字查找物体快得多。标签最多只能有 32个。前几个是常用标签,具有特定含义,例如玩家( Player)、主摄摄像机 (Mai…...
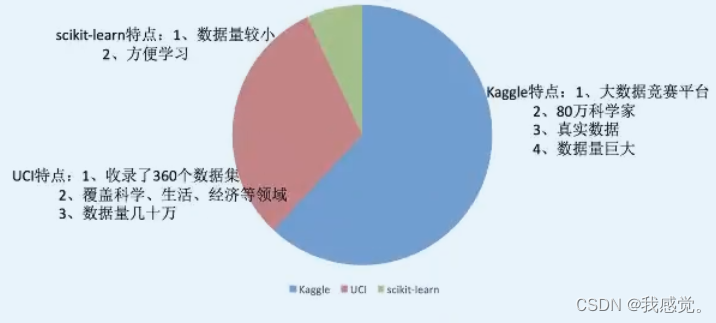
【黑马程序员】机器学习
(一)机器学习概述 一、机器学习算法分类 1、监督学习: (1)目标值是类别:分类问题 k-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归 (2)目标值是连续型的数据:回归…...

flutter card 使用示例
Card组件是卡片组件,内容可以由列表的widget组成,Card组件具有阴影圆角的功能。 常用属性: 属性 说明 margin 外边距elevation 阴影值的深度child 子元素 import package:flutter/material.dart;void main() > runApp(MyApp());class M…...

推荐算法:是否对用户判断能力有影响!!!
首先认识几种常见的推荐算法:推荐算法是一种在信息推送和个性化服务领域常用的技术。它通过分析用户的兴趣、行为和偏好,提供个性化的建议和推荐,以满足用户的需求。以下是对几种常见推荐算法的重新排版,并探讨了它们的作用、影响…...
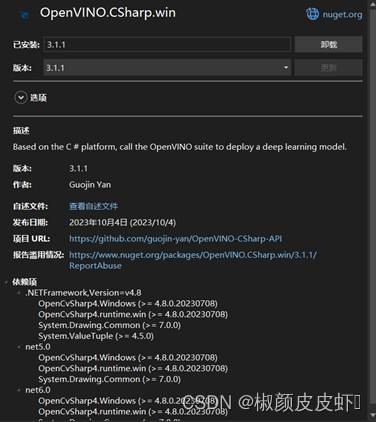
【OpenVINO】OpenVINO C# API 常用 API 详解与演示
OpenVINO C# API 常用 API 详解与演示 1 安装OpenVINO C# API2 导入程序集 3 初始化OpenVINO 运行时内核4 加载并获取模型信息4.1 加载模型4.2 获取模型信息 5 编译模型并创建推理请求6 张量Tensor6.1 张量的获取与设置6.2 张量的信息获取与设置 7 加载推理数据7.1 获取输入张量…...
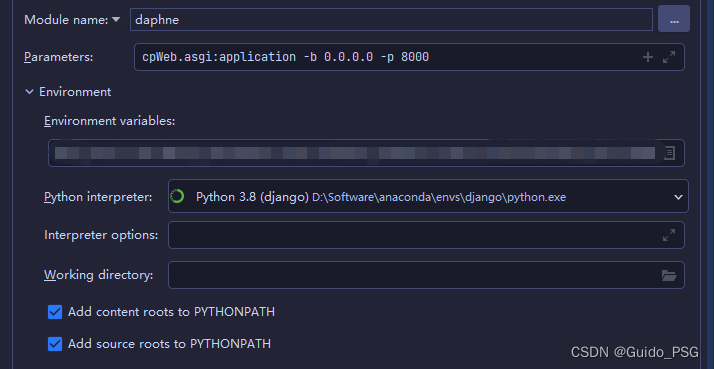
django无法导入第三方库
引子 有的人可能会很困惑,为什么自己在pip中安装了某个包,但是在django中死活无法导入。 在cmd中能够导入。 启动django,总是无法导入。 本文将会用一分钟解决你的困惑。 正文 那么本文以上述的第三方库dj_db_conn_pool为例,…...

7-k8s-helm管理
文章目录 一、为什么需要Helm二、Helm相关概念介绍三、Helm安装四、Helm指令介绍五、Helm创建tomcat六、Helm创建tomcat其他方式七、Helm创建redis 一、为什么需要Helm k8s部署:k8s平台部署的服务都是由资源文件描述组成,传统的k8s部署应用需要手工编排…...

零基础怎么样才能学好 Python?Python 入门必看
Python 目前可以用一个字来描述那就是 “火”,问题来了,这么火的语言零基础小白到底该怎样学习 Python? 首先,从基础开始学习,切勿毛躁。 刚开始学习 Python 的时候,我们可能会有些毛躁总觉得这些知识太简…...

1.X3-Warming up
/* 此程序使用 Boost Spirit 库来解析用户提供的逗号分隔的数字列表。它演示了如何使用 Spirit 来定义解析 器和执行解析操作,并且在用户输入时反复执行解析操作。用户可以提供一系列逗号分隔的数字,程序会检查它们 是否符合指定的解析规则。如果解析成功…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
