位运算基础知识及性质(精简总结)
目录
简介
基础知识
常用性质
简介
程计算机中的数在内存中都是以二进制形式进行存储的,用位运算就是直接对整数在内存中的二进制位进行操作,因此其执行效率非常高,在程序中尽量使用位运算进行操作,这会大大提高程序的性能。
基础知识
- 与运算(&):两个数的对应位都为1时结果为1。
- 或运算(|):两个数的对应位有一个为1时结果为1。
- 异或运算(^):两个数的对应位不相同时结果为1。
- 非运算(~):一个数的每个位取反。
- 左移(<<):二进制表示左移若干位,每左移一位,相当于该数乘以2
- 右移(>>):二进制表示右移若干位,每右移一位,相当于该数除以2
常用性质
- 任何数与 0 进行与运算都是 0
- 任何数与 0 进行或运算都是本身
- 双重非运算可以使得小数快速取整
- 任何数与自己进行异或运算都为 0,所以任何数与 0 进行异或运算都是本身
x^x=0,x^0=x (比较两值是否相等)
- 实现乘除法
数 a 向右移一位,相当于将 a 除以 2;数 a 向左移一位,相当于将 a 乘以 2
- 异或完成变量值交换
//位与操作 void swap(int &a, int &b) {a ^= b;b ^= a;a ^= b; }
- 与 1 进行与运算可以用来判断数的奇偶
只要根据数的最后一位是 0 还是 1 来决定即可,为 0 就是偶数,为 1 就是奇数
- (a |= 1 << i) :将第 i + 1 个二进制位设为 1
- [ a &= ~(1 << i) ] :将第 i + 1 个二进制位设为 0
相关文章:
)
位运算基础知识及性质(精简总结)
目录 简介 基础知识 常用性质 简介 程计算机中的数在内存中都是以二进制形式进行存储的,用位运算就是直接对整数在内存中的二进制位进行操作,因此其执行效率非常高,在程序中尽量使用位运算进行操作,这会大大提高程序的性能。 基…...
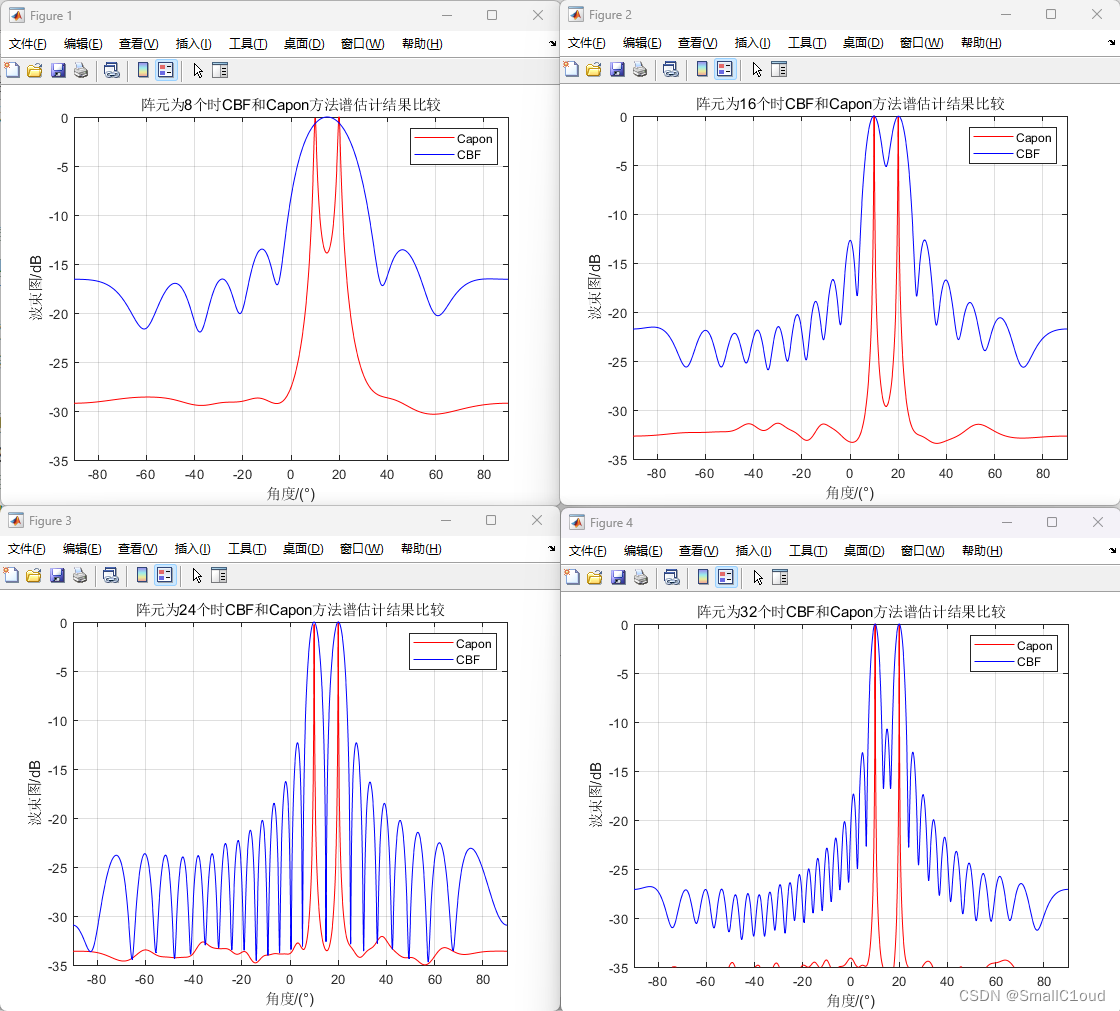
阵列信号处理_对比常规波束形成法(CBF)和Capon算法
空间谱估计 利用电磁波信号来获取目标或信源相对天线阵列的角度信息的方式,也称测向、波达方向估计(DOA)。主要应用于雷达、通信、电子对抗和侦察等领域。 发展 常规波束形成(CBF)。本质是时域傅里叶变换在空域直接…...

通过循环生成多个echarts图表并实现自适应
不推荐使用grid布局,不清楚为什么左边一列的不会自适应,换成flex布局就可以了 主要方法借助中的getInstanceByDom方法 完整代码: <template><div class"statis"><div class"content" ><!-- v-for …...
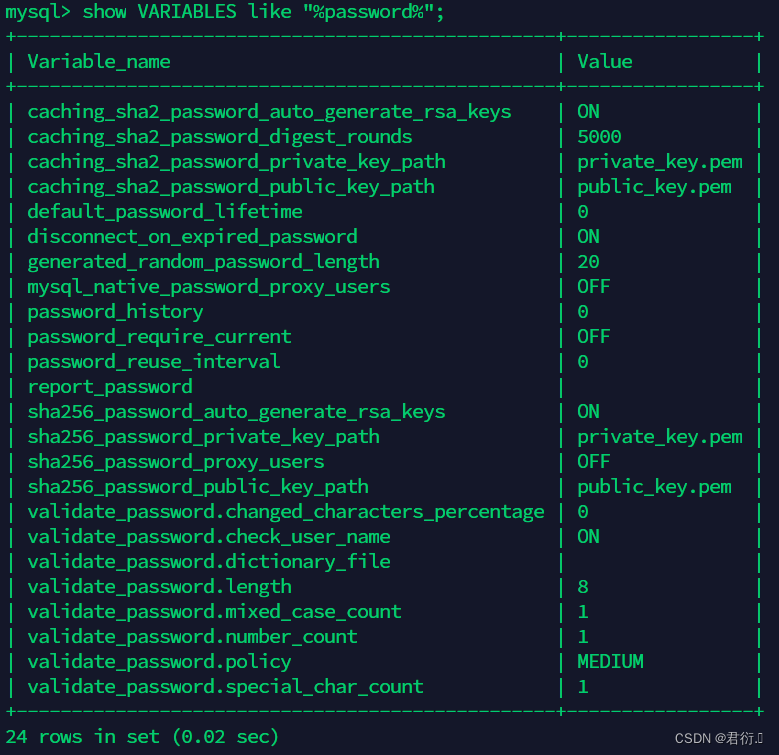
MySQL——六、库表操作(下篇)
MySQL 一、INSERT语句二、REPLACE语句三、UPDATE语句四、delete和TRUNCATE语句五、MySQL用户授权1、密码策略2、用户授权和撤销授权 一、INSERT语句 #在表里面插入数据:默认情况下,一次插入操作只插入一行 方式1: INSERT [INTO] 表名 [(colu…...

自动化办公篇之python批量改名
#批量命名 import xlwings as xw app xw.App(visibleFalse,add_bookFalse) workbook app.books.open("测试表.xlsx") for sheet in workbook.sheets:sheet.namesheet.name.replace("彩印之","银河") workbook.save() app.quit()...
Android MediaCodec将h264实时视频流数据解码为yuv,并转换yuv的颜色格式为nv21
初始化mediacodec private MediaCodec mediaCodec;private ByteBuffer[] inputBuffers;private void initMediaCodec(Surface surface) {try {Log.d(TAG, "onGetNetVideoData: ");//创建解码器 H264的Type为 AACmediaCodec MediaCodec.createDecoderByType("v…...

Postgresql SQL 字段拼接
本文介绍Postgresql 数据库sql字段拼接的方法。 1.使用字符串连接函数 select pkey || - || vname as "项目-版本" from test_jira_project_verison; 2.使用字符串连接操作符 select CONCAT(pkey, -, vname) as "项目-版本" from test_jira_project_ve…...

MySQL 迁移完不能快速导数据了?
关于 5.6 升级到 5.7 之后,GTID 的相关功能的注意事项。 作者:秦福朗,爱可生 DBA 团是队成员,负责项目日常问题处理及公司平台问题排查。热爱互联网,会摄影、懂厨艺,不会厨艺的 DBA 不是好司机,…...

Lazysysadmin靶机
信息收集 主机发现 nmap -sn 192.168.88.0/24 //-sn:制作主机发现,不做端口扫描;扫描结果包含本机IP 端口扫描 nmap --min-rate 10000 -p- 192.168.88.136 扫描端口详细信息 端口扫描发现,该主机的22、80、139、445、3306、…...
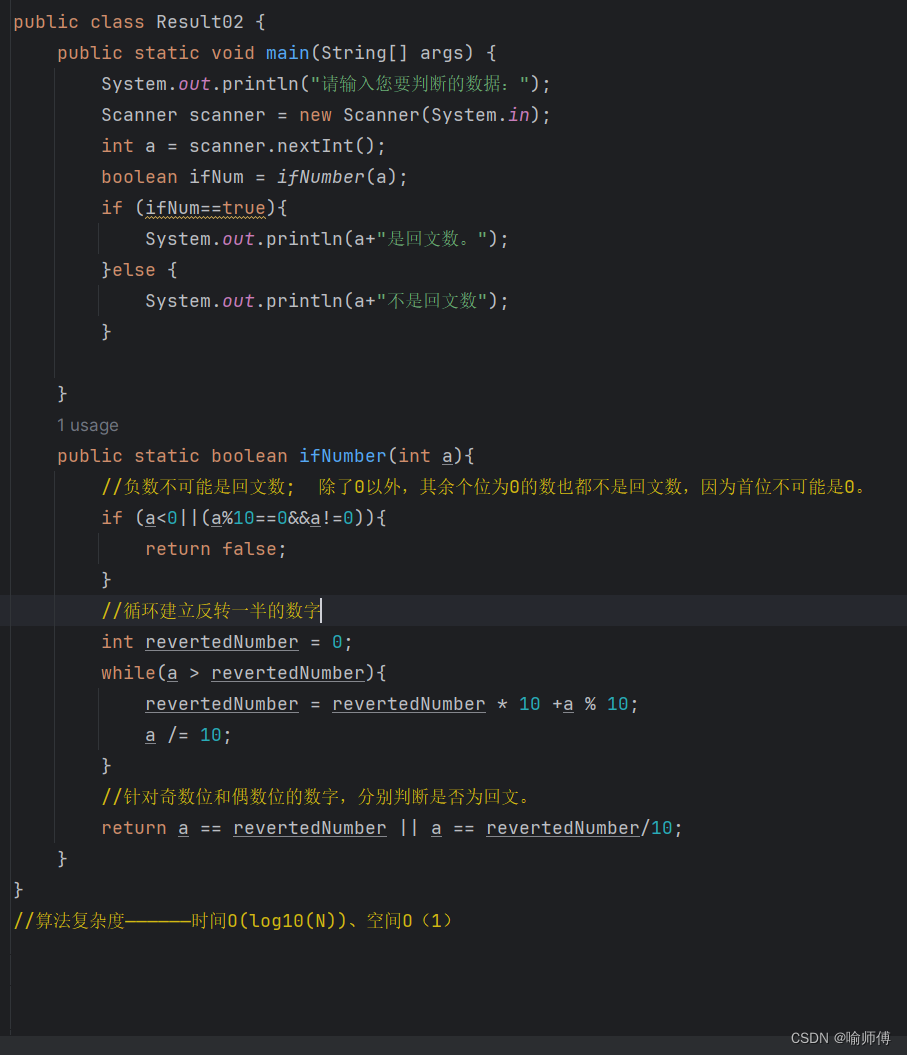
LeetCode09——回文数
LeetCode09 自己写的解,转化为字符串再反转,比较笨。 import java.util.Scanner; public class Result01 {public static void main(String[] args) {System.out.println("请输入整数,我来帮您判断是否是回文数。");Scanner scanner new Sc…...
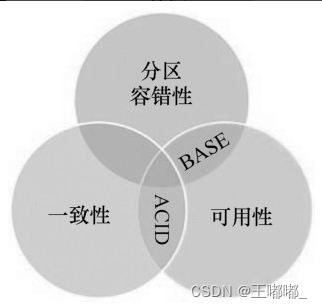
云安全—分布式基础
0x00 前言 云必然是依赖于分布式技术来进行实现的,所以有必要学习和来了解分布式相关的内容 0x01 分布式计算 1.基本概述 分布式计算的定义:通过网络互联的计算机都具有一定的计算能力,他们之间互相传递数据,实现信息共享&…...
Spring(18) @Order注解介绍、使用、底层原理
目录 一、简介二、List 注入使用示例2.1 测试接口类2.2 测试接口实现类12.3 测试接口实现类22.4 启动类(测试)2.5 测试结果场景一:场景二: 三、CommandLineRunner 使用示例3.1 接口实现类13.2 接口实现类23.3 测试结果场景一&…...

目标检测YOLO实战应用案例100讲-基于改进YOLOv6的轧钢表面细小缺陷检测
目录 前言 存在的问题 轧钢缺陷图像特征分析 2.1单一类型缺陷 2.2面状缺陷...

leetcode:507. 完美数(python3解法)
难度:简单 对于一个 正整数,如果它和除了它自身以外的所有 正因子 之和相等,我们称它为 「完美数」。 给定一个 整数 n, 如果是完美数,返回 true;否则返回 false。 示例 1: 输入:num…...

智能物联网解决方案:蓝牙IOT主控模块打造高效监测和超低功耗
物联网蓝牙模块,无论单模,还是双模,或者双模音频的选择,如下文说描述: 蓝牙芯片模块市场的百花齐放,也带来的工程师在选型时碰到很大的困难,但是无论是做半成品,还是做成品…...
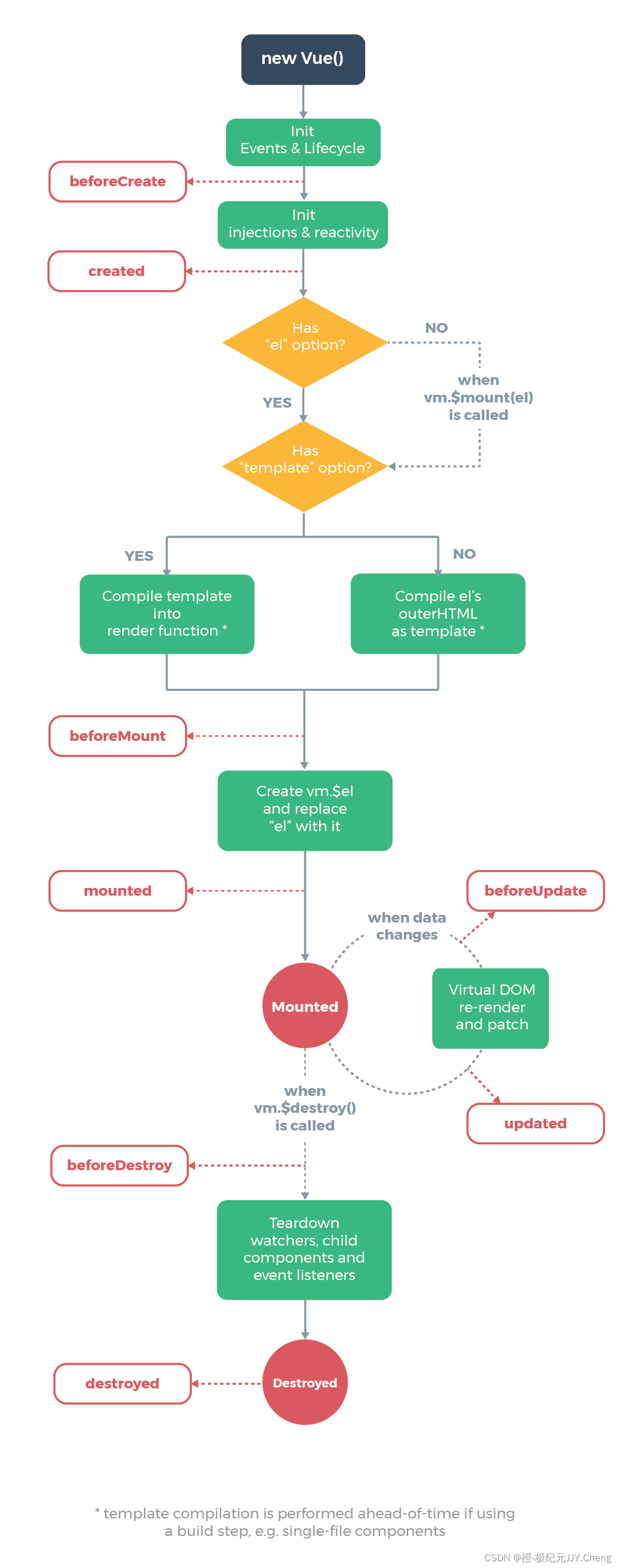
vue 拿到数据后,没有重新渲染视图,nuxt.js拿到数据后,没有重新渲染视图,强制更新视图
以下为Vue2的解决方案 一、 Vue.set() 问:什么情况下使用? 答:如果你向响应式数据添加新的“属性”,理论上,一般情况下是没问题的,但是,如果你的级别比较深,又…...
Docker基础操作命令演示
Docker中的常见命令,可以参考官方文档:https://docs.docker.com/engine/reference/commandline/cli/ 1、常见命令介绍 其中,比较常见的命令有: 命令说明文档地址docker pull拉取镜像docker pulldocker push推送镜像到DockerReg…...

XTU-OJ 1175-Change
题目描述 一个班有N个学生,每个学生有第一学期成绩Xi,第二学期成绩Yi,请问成绩上升,持平,下降的人数。 输入 每个样例的第一行是整数N(0≤N≤50),如果N0,表示输入结束,这个样例不需要处理。 第二行是N个整数…...

Python环境安装
环境安装 Windows安装Linux安装 Windows安装 下载最新版Python https://www.python.org/downloads 打开安装包 选择安装路径,安装 安装 验证安装是否成功,命令行输入python Linux安装 安装依赖环境 yum install wget zlib-devel bzip2-devel op…...

苏轼在密州的四首千古名作
苏轼,一个从诗歌王国掉落人间的落魄贵族,整个政治生涯几乎都以流浪为主,在古诗词世界或许只有李白与之最是相似,不过李白的流浪属于荡歌山水、云游四方,而苏轼的流浪则带有被动的成分:一纸贬黜公文就是苏轼…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
