C语言 形参、实参
定义
形参
形式上的参数，没有确定的值
实参
实际存在的，已经确定的参数，常量，变量，表达式，都是实参
区别
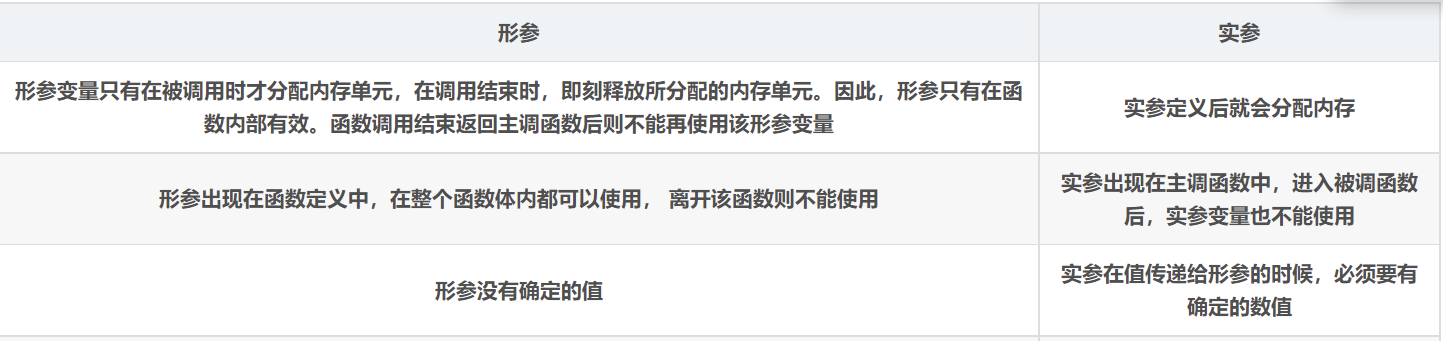
实参的值不随形参的变化而变化
在C语言中，数据传送是单向的，即只能把实参的值值传递给形参，但形参的变化不会改变实参的值，我们可以简单理解，就相当于把实参的值 复制给了另一个数（形参），而另一个数的改变不会改变原来数（实参）的值，正规来说：他们在内存中位于不同的位置，形参将实参的内容复制一份，在该函数运行结束的时候形参被释放，而实参内容不会改变。
实参传递给形参的参数个数类型和顺序都应相同
实参传递给形参的参数个数类型和顺序都应相同，否则会系统强制转换，出现数据丢失或者 “类型不匹配”的错误。
如果实参是数组名，那么形参传递的之就是地址的值
在C里面 是无法做到形参改变 实参值同步改变的
如果要用函数改变实参的值，可以用指针作为参数来改变。
形参和实参虽然可以同名，但它们之间是相互独立的，互不影响，因为实参在函数外部有效，而形参在函数内部有效
相关文章：
C语言 形参、实参
定义 形参 形式上的参数，没有确定的值 实参 实际存在的，已经确定的参数，常量，变量，表达式，都是实参 区别 实参的值不随形参的变化而变化 在C语言中，数据传送是单向的，即只能把实…...
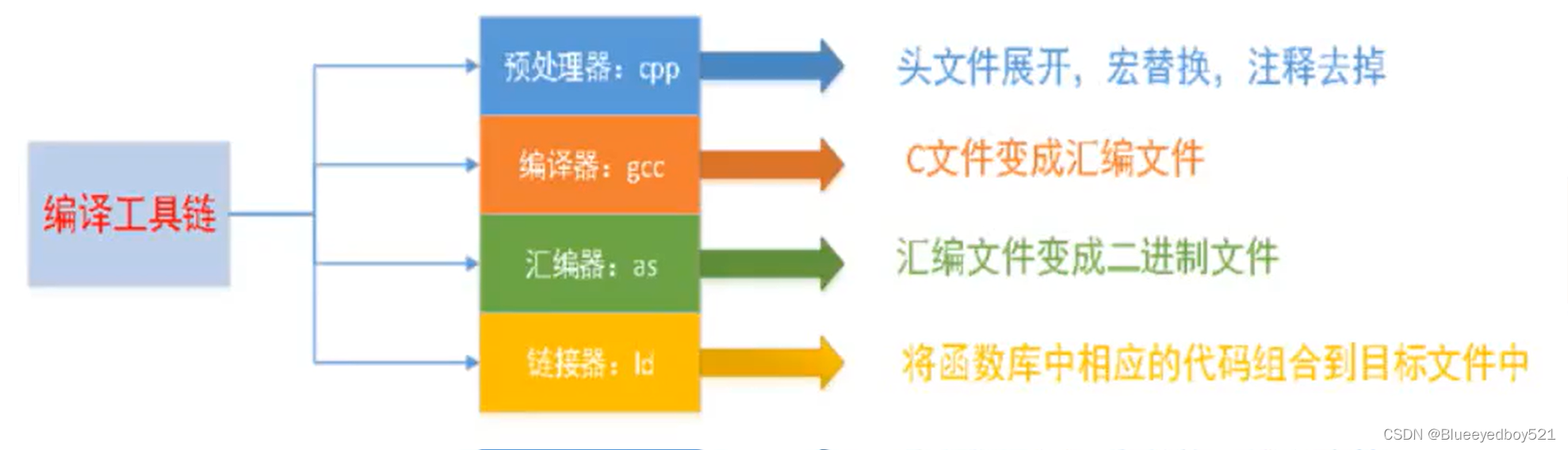
linux入门到精通-第四章-gcc编译器
目录 参考gcc概述gcc的工作流程 参考 gcc编译器 gcc概述 编辑器vi、记事本)是指我用它来写程序的 (编辑码)，而我们写的代码语句，电脑是不懂的，我们需要把它转成电脑能懂的语句，编译器就是这样的转化工具。就是说，我…...
HCIP静态路由综合实验
题目： 步骤： 第一步：搭建上图所示拓扑; 第二步：为路由器接口配置IP地址； R1： [R1]display current-configuration intinterface GigabitEthernet0/0/0ip address 192.168.1.1 255.255.255.252 interfa…...
)
nginx前端配置(新)
基础配置 server {listen 80;server_name your-frontend-domain.com;# 根目录为前端网页文件所在目录root /path/to/your/frontend/files;# 默认文档（例如 index.html）index index.html;location / {try_files $uri $uri/ /index.html; #try_files 指…...
js,jquery,vue设置html标签隐藏不显示
前端 <p id"myElement"> </p>使用js将idmyElemnt的标签隐藏 使用 style.display 属性： 通过设置 style.display 属性为 "none"，可以隐藏标签。 var element document.getElementById("myElement");element…...
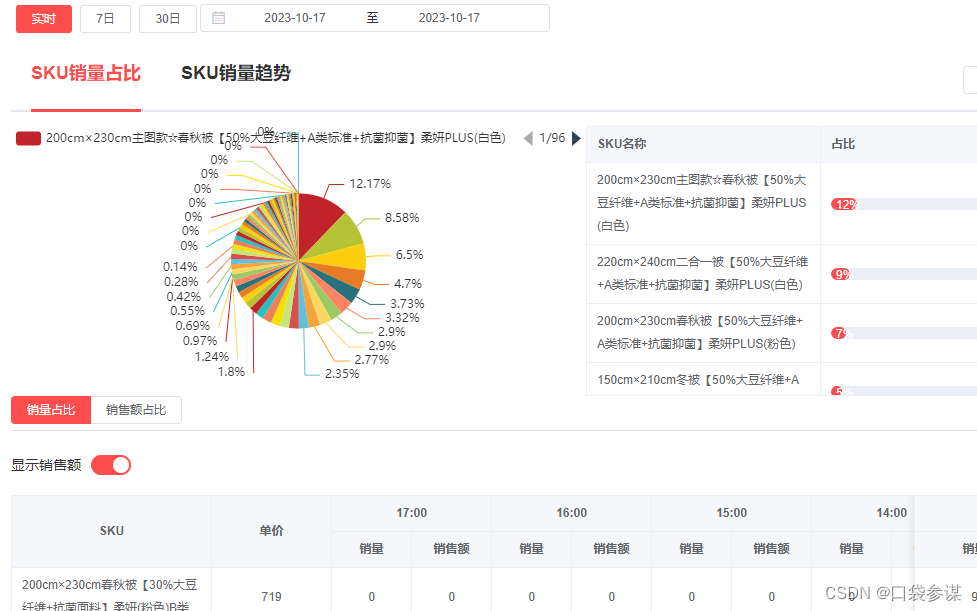
口袋参谋：如何实时监控对手数据？
在如此激烈的淘宝天猫上开店，如何才能获取对手的数据呢？ 俗话说的好，知己知彼百战百胜，那么这句话同样也适用于淘宝天猫上。 只有掌握对手推广策略以及数据，我们才有机会反超，因此做好竞品监控是运营店…...
Q-learning如何与ABC等一些元启发式算法能够结合在一起？
1、出现的问题 Q-learning能和元启发式算法（如ABC、PSO、GA、SSA等）结合在一起，实现工作流调度问题？ Q-learning和ABC (Artificial Bee Colony) 等元启发式算法可以结合在一起以解决特定类型的问题。Q-learning是一种强化学习算法…...
mysql 过滤多列重复的值（保留其中一条），对单列或者多列重复的值去重
建立测试数据表 CREATE TABLE test (id int(11) NOT NULL AUTO_INCREMENT,account varchar(255) DEFAULT NULL,password varchar(255) DEFAULT NULL,deviceId varchar(255) DEFAULT NULL,PRIMARY KEY (id) ) ENGINEInnoDB AUTO_INCREMENT11 DEFAULT CHARSETutf8mb4;INSERT INT…...
面向红队的自动化引擎工具
gogo 介绍 面向红队的、高度可控的可拓展的自动化引擎。特征如下： 自由的端口配置 支持主动/主动指纹识别 关键信息提取，如标题、证书以及自定义提取信息的正则 支持nuclei poc，poc目录：https://chainreactors.github.io/wiki/…...
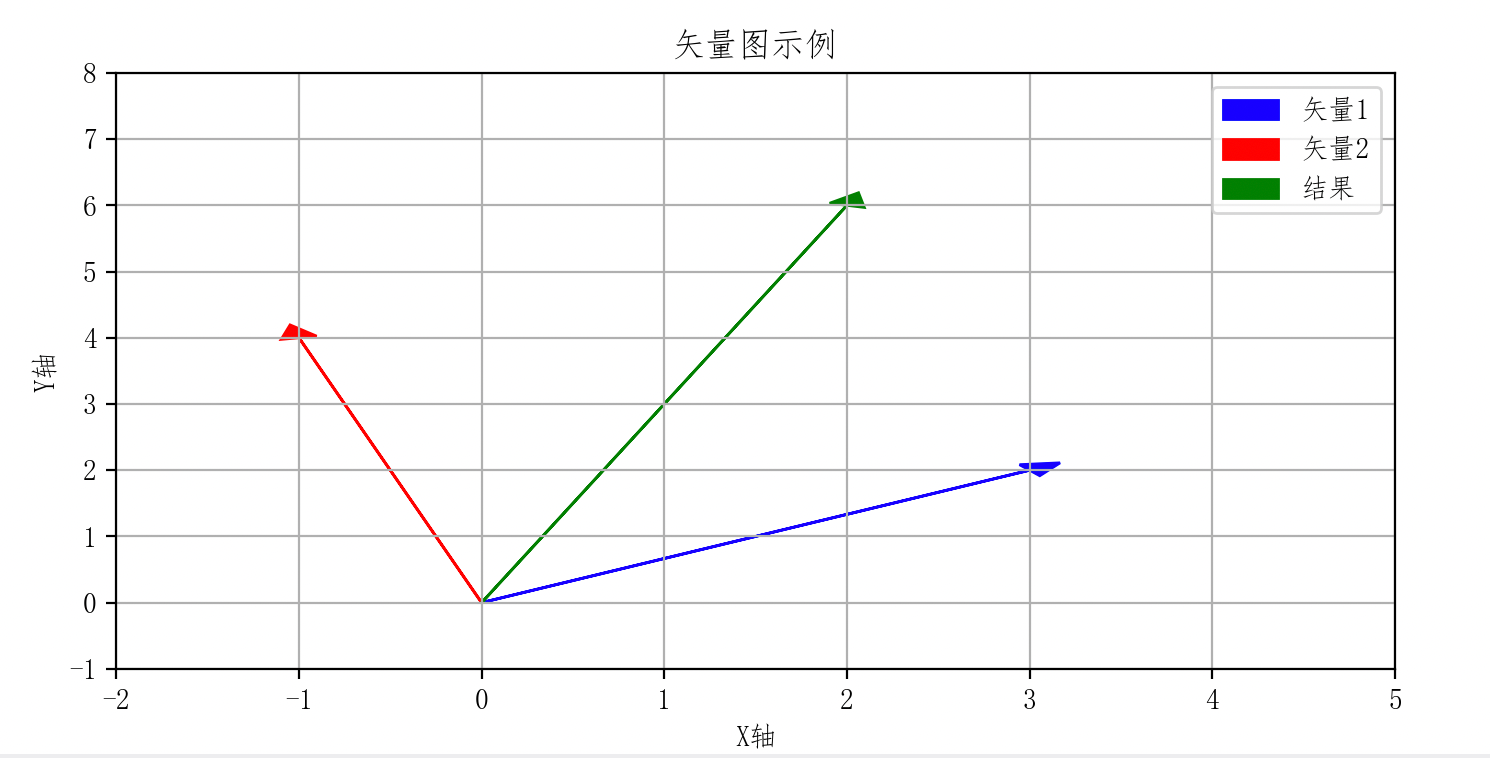
Python库学习(十):Matplotlib绘画库
1. 介绍 Matplotlib 是一个用于绘制图表和可视化数据的 Python 库。它提供了丰富的绘图工具，可以用于生成各种静态、交互式和动画图表。Matplotlib 是数据科学、机器学习和科学计算领域中最流行的绘图库之一。 1.1 关键特性 以下是 Matplotlib 的一些关键特性&…...
coverity工具 代码审计
第39篇：Coverity代码审计/代码扫描工具的使用教程_希潭实验室ABC123的博客-CSDN博客...
女鹅冬天的第一件羽绒服，当然要时尚经典的
90白鸭绒，高密度充绒量和蓬松度 让这件羽绒服更加饱满更有型 三防工艺，立领连帽设计 下摆抽绳，帽子上的魔术贴设计 无一不将保暖落实在实处 宽松版型立体感很强，对身材的包容性也是非常不错...
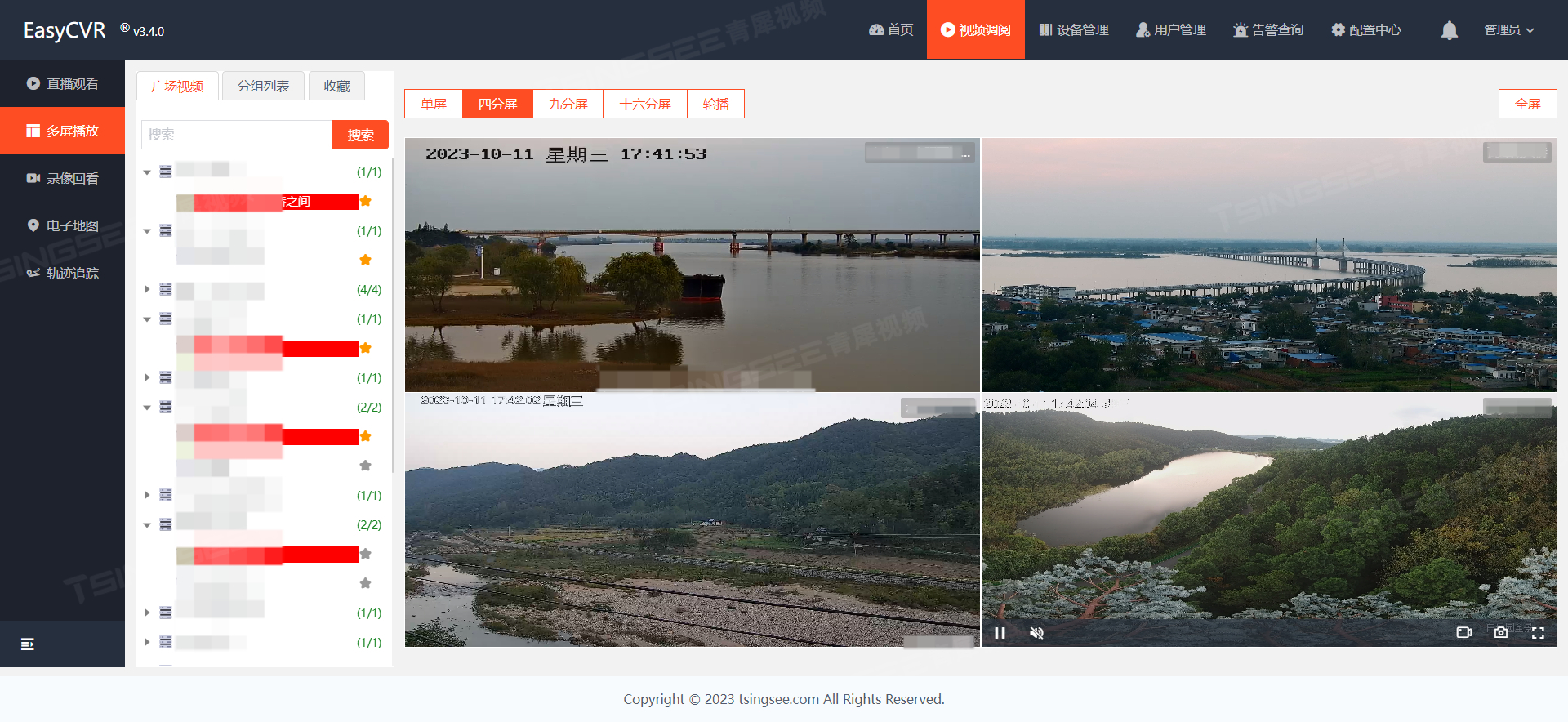
智慧渔业方案：AI渔政视频智能监管平台助力水域禁渔执法
一、方案背景 国内有很多水库及河流设立了禁渔期，加强渔政执法监管对保障国家渔业权益、维护渔业生产秩序、保护渔民群众生命财产安全、推进水域生态文明建设具有重要意义。目前，部分地区的监管手段信息化水平低下，存在人员少、职责多、任务…...
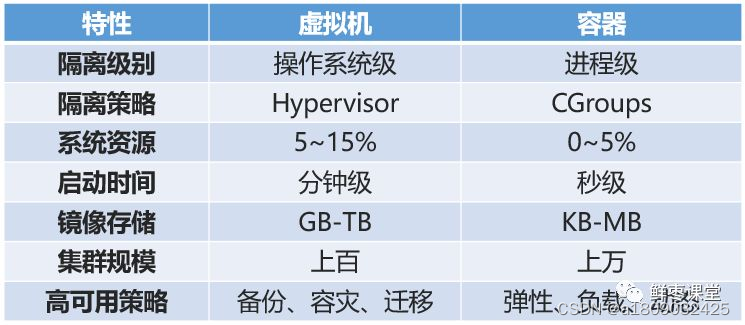
LXC、Docker、 Kubernetes 容器以及Hypervisor的区别
LXC、Docker、 Kubernetes 容器以及Hypervisor的区别 SaaS: Software-as-a-Service（软件即服务） PaaS: Platform-as-a-Service（平台即服务） IaaS: Infrastructure-as-a-Service（基础设施即服务） 1、Docke…...
电子杂志制作不求人：简单易用的工具推荐
如果你想要制作一份精美的电子杂志，但是又不想花费太多的时间和金钱，也不想求及朋友帮忙制作，那么可以试试这个网站制作电子杂志，展现出的效果跟专业级设计师的效果没什么区别哦 赶快收藏吧-------FLBOOK在线制作电子杂志平台&a…...
Excel冻结窗格
1、冻结表格首行 点击菜单栏中的“视图”，选择“窗口”选项卡中的“冻结窗格”下的小三角，再选择“冻结首行”； 2.冻结表格首列 点击菜单栏中的“视图”，选择“窗口”选项卡中的“冻结窗格”下的小三角，再选择“冻结…...
Flink自定义sink并支持insert overwrite 功能
前言 自定义flink sink，批模式下，有insert overwrite 需求或需要启动任务或任务完成后时，只执行一次某些操作时，则可参考此文章 组件： flink: 1.15 参考文档：https://nightlies.apache.org/flink/flink-docs-release-1.15/docs/dev/table/sourcessinks/ 分析 inser…...
CSS Vue/RN 背景使用opacity，文字在背景上显示
Vue <div class"training_project_tip"> <div class"tip">展示的文字</div> </div> .training_project_tip { font-size: 12px; font-weight: 400; text-align: left; color: #ffffff; margin-top: 8px; position: relative; dis…...
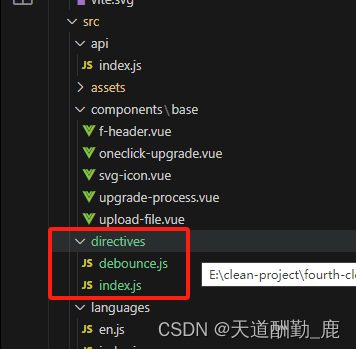
vue3自定义指令批量注册
第一步、在src目录下新建directives文件文件夹 用来存放不同的指令，以dbounce指令为例： 第二步、在directives目录下创建debounce.js文件，文件内容如下： // 防抖 const debounceClick {mounted(el, binding) {let timerel.addE…...
山西电力市场日前价格预测【2023-10-18】
日前价格预测 预测说明： 如上图所示，预测明日（2023-10-18）山西电力市场全天平均日前电价为348.72元/MWh。其中，最高日前电价为505.50元/MWh，预计出现在18: 00。最低日前电价为288.10元/MWh，预计…...
装饰模式（Decorator Pattern）重构java邮件发奖系统实战
前言 现在我们有个如下的需求，设计一个邮件发奖的小系统， 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式（Decorator Pattern）允许向一个现有的对象添加新的功能，同时又不改变其…...
论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）
HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...
DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽，大家好，我是左手python！ Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库，用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣（LeetCode） 思路 使用两个栈：一个存储重复次数，一个存储字符串 遍历输入字符串： 数字处理：遇到数字时，累积计算重复次数左括号处理：保存当前状态&a…...
抖音增长新引擎：品融电商，一站式全案代运营领跑者
抖音增长新引擎：品融电商，一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中，品牌如何破浪前行？自建团队成本高、效果难控；碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...
视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞！！！ 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用，因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型（VLMs）在字幕生成方面…...
DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API，查询的是单条数据，比如根据主键ID查询用户信息，sql如下： select id, name, age from user where id #{id}API默认返回的数据格式是多条的，如下： {&qu…...
QT： `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中，将 long long 类型转换为 QString 可以通过以下两种常用方法实现： 方法 1：使用 QString::number() 直接调用 QString 的静态方法 number()，将数值转换为字符串： long long value 1234567890123456789LL; …...
服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行！ sudo su - 1. CentOS 系统： yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定，这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中，积分电荷法最为常用，其原理是通过测量在电容器上积累的热释电电荷，从而确定热释电系数…...