51单片机点阵
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、点阵是什么?
- 1.点阵的原理
- 2. 3*3 点阵显示原理
- 3. 8*8点阵实物图
- 4. 8*8点阵内部原理图
- 5. 16*16点阵实物图,显示原理
- 二、使用步骤
- 1.先看原理图,确定点阵是8*8 16*16 ,共阴,共阳?
- 2.写代码
- 核心问题,段码怎么来?
- 三、实物操作
- 1.原理图
- 2.编程思路
- 四、 书上的代码讲解
- 总结
前言
学习了数码管的静态和动态显示,利用动态数码管显示的原理,搞定点阵。
一、点阵是什么?
1.点阵的原理
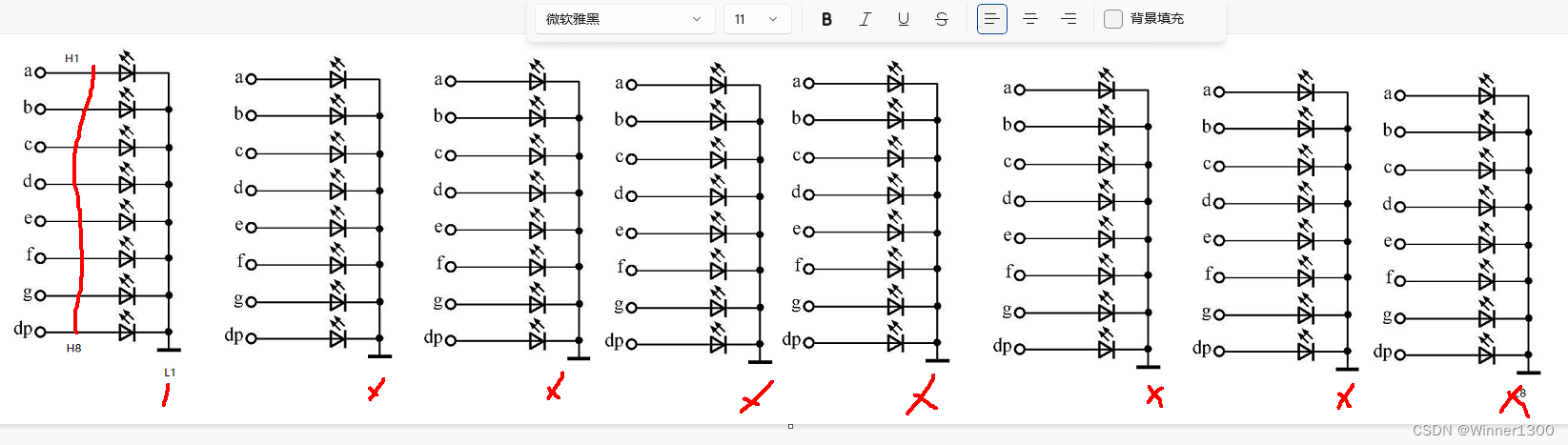
2. 3*3 点阵显示原理
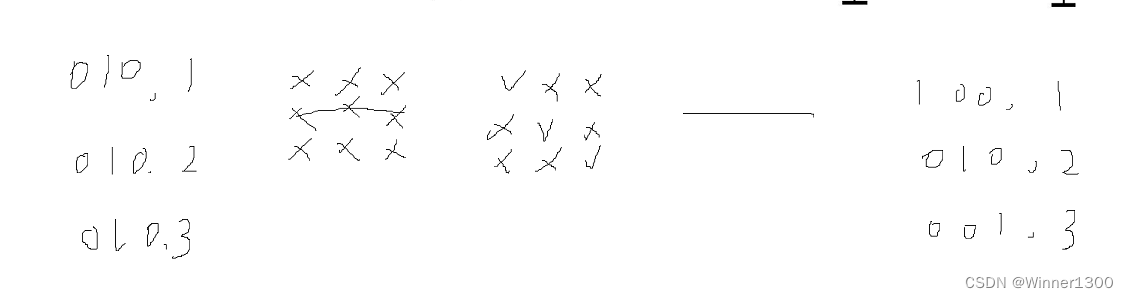
3. 8*8点阵实物图

4. 8*8点阵内部原理图

5. 16*16点阵实物图,显示原理
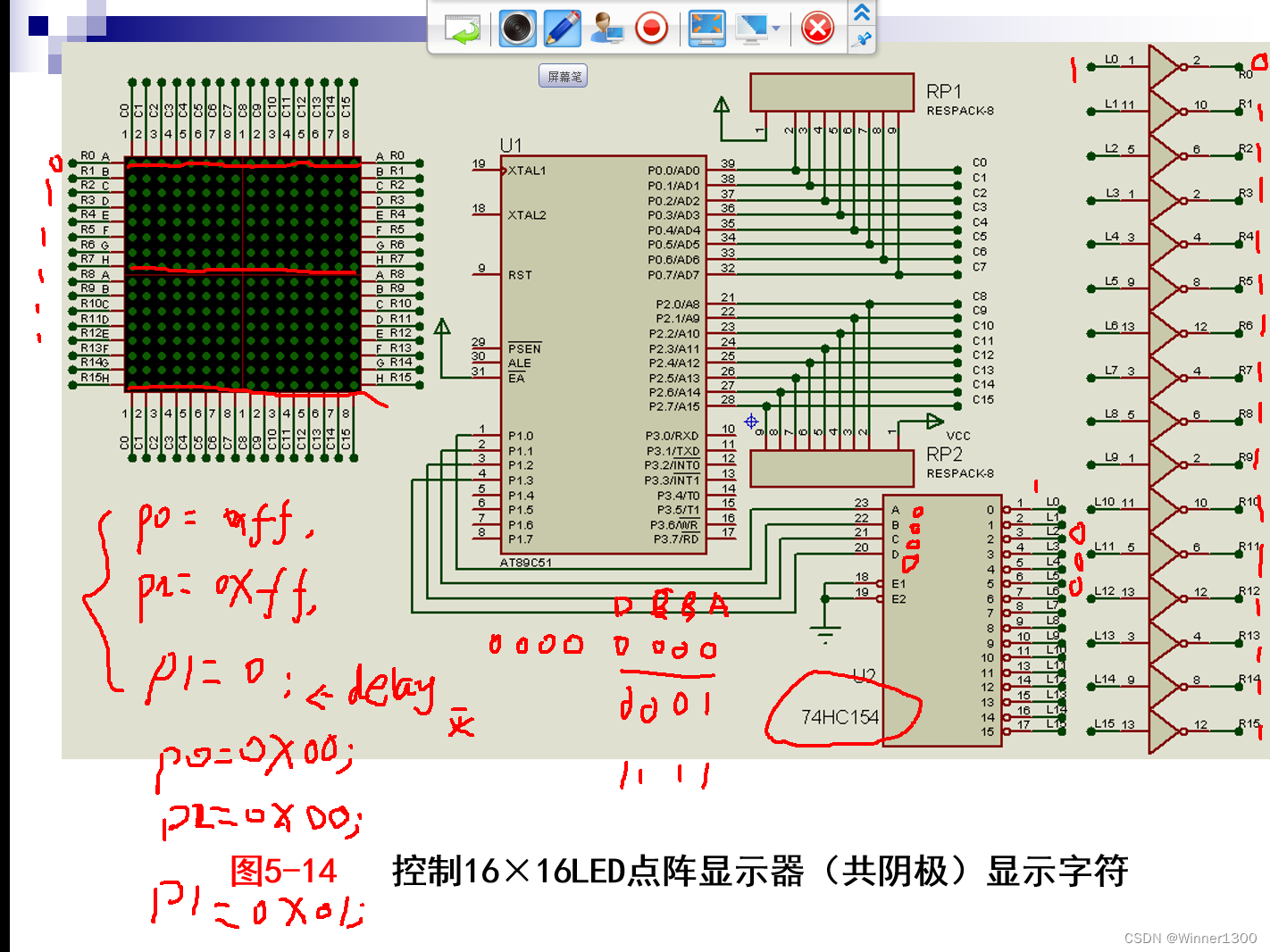
二、使用步骤
1.先看原理图,确定点阵是88 1616 ,共阴,共阳?
代码如下(示例):
取段码:用专门的软件。
2.写代码
代码如下(示例):
逐行:第一行
1.先给段码
P0=0X?
P2=0X?
P1=0X00;第一行
1.先给段码
P0=0X?
P2=0X?
P1=0X01;0000~1111 0-15for(i=0;i<16;i++)
{P0=0X?P2=0X?P1=i;delay(?);P0=0X00;P2=0X00;}核心问题,段码怎么来?
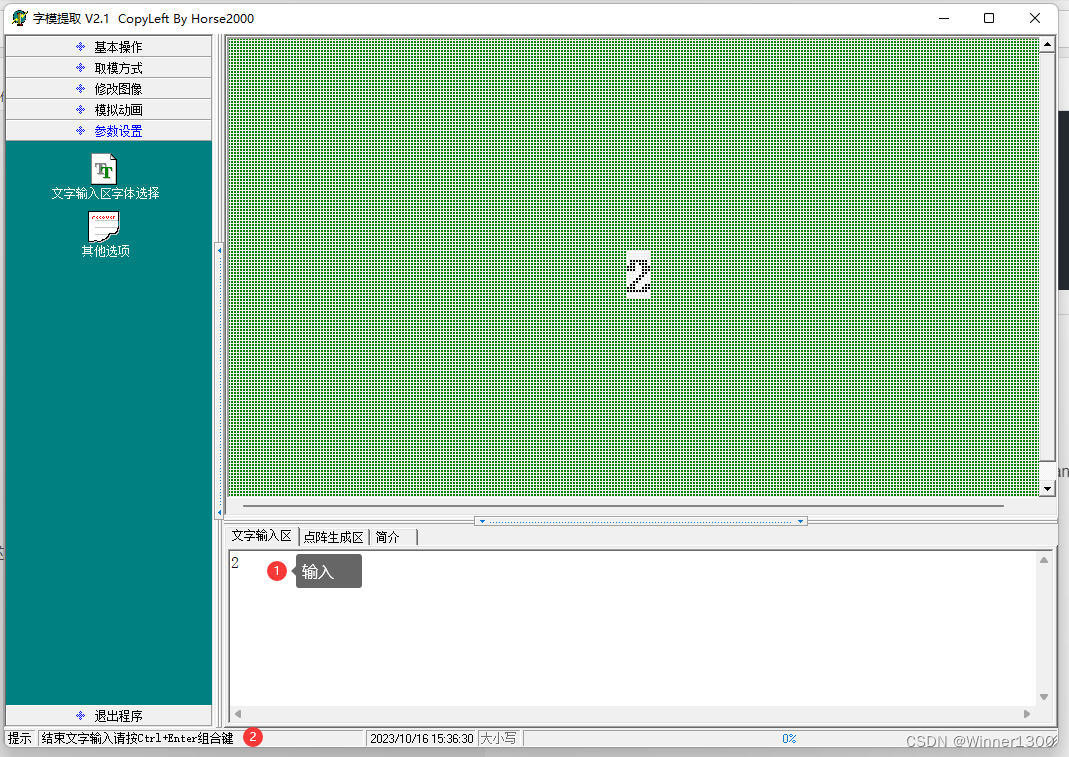
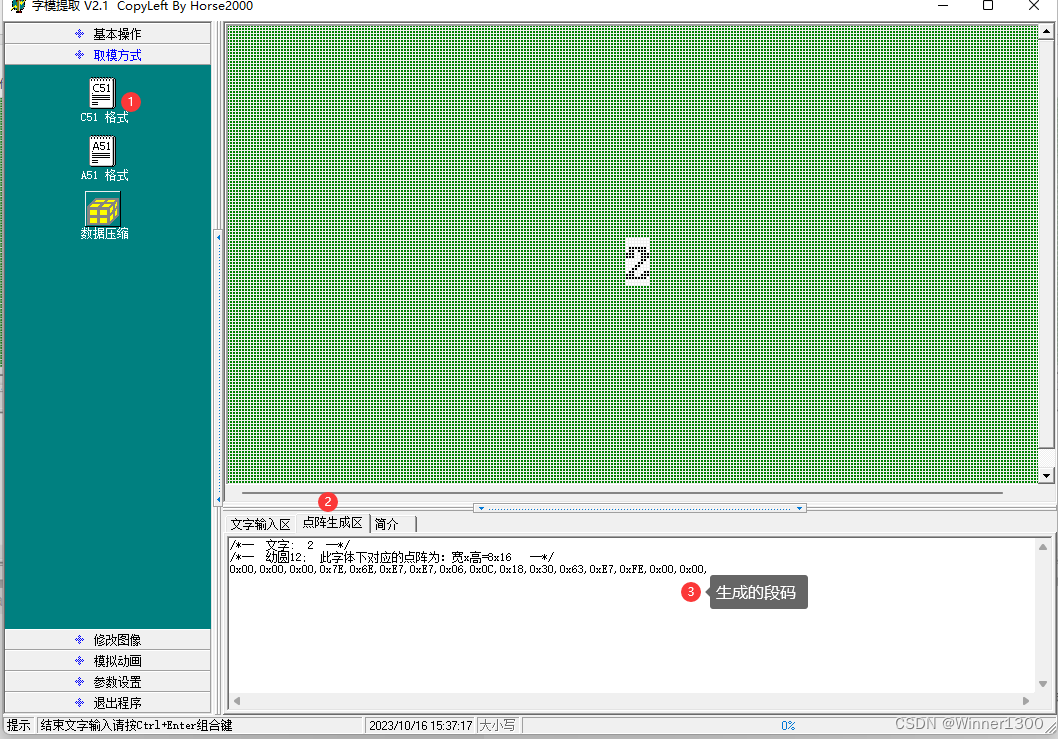
三、实物操作
1.原理图

2.编程思路
- 段码 P0=0X?
- 位选
P35 pclk
P36 srclk
P34 SER
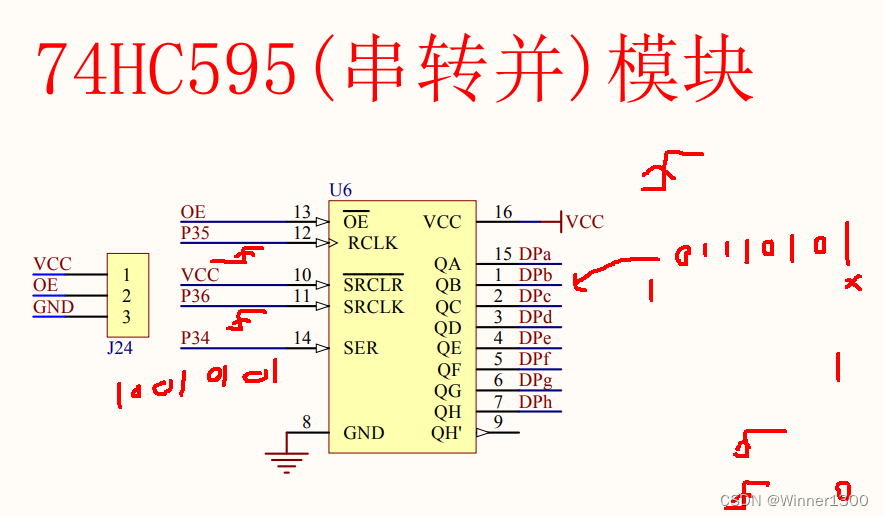
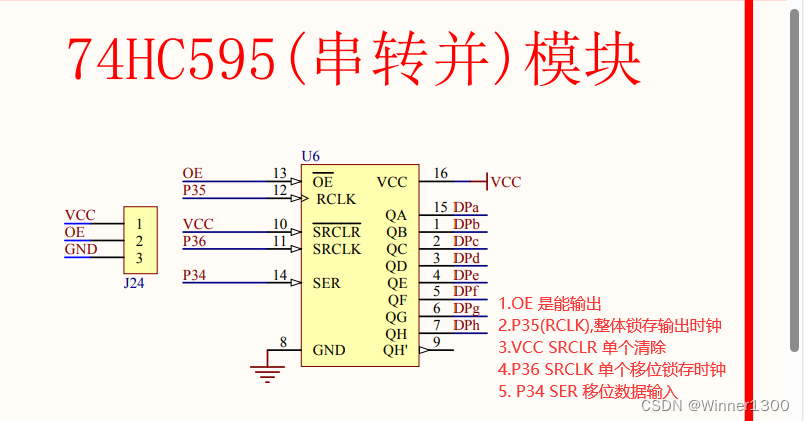
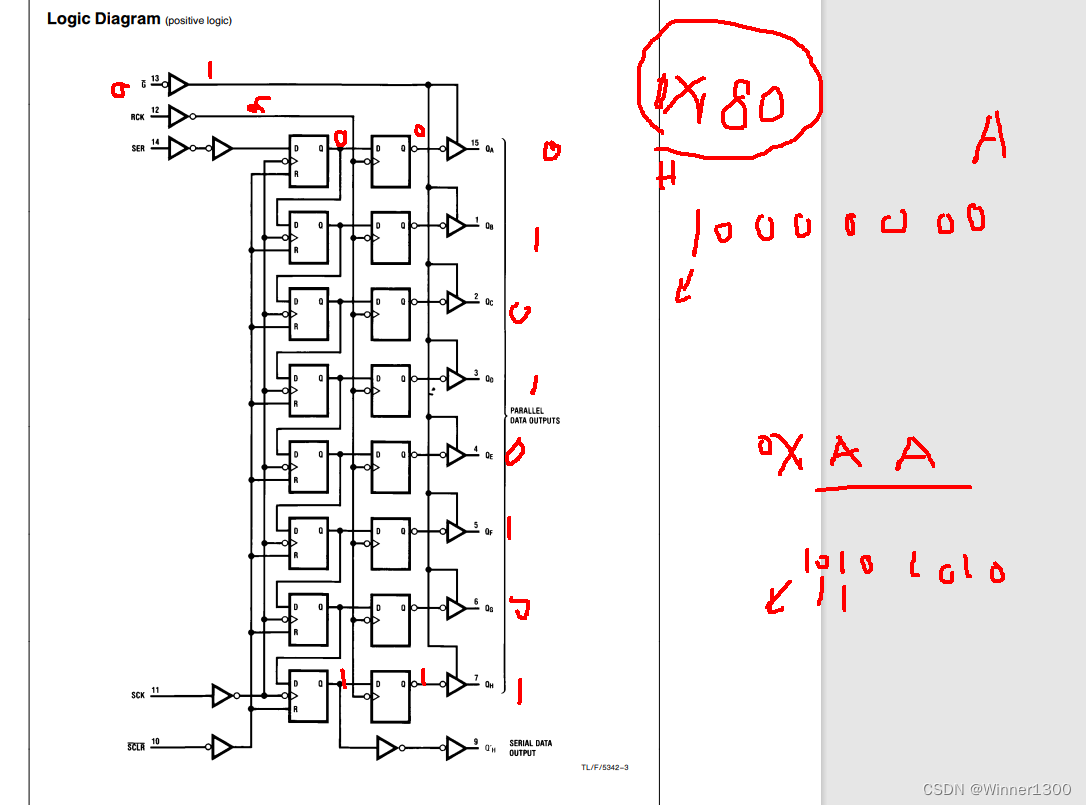
J24 接 GND
P35_RCLK
P34_data
P36_SRCLK
一次移位
P34_data=1;
P36_SRCLK=0;
P36_SRCLK=1;八次移位:
最简单的方法将上面的代码赋值八次
P34_data=?; // 是0 给00,是1给1
P36_SRCLK=0;
P36_SRCLK=1;
........P35_RCLK=0;
P35_RCLK=1;//发送 x =0x01 第一行// 0000 0001
// 1000 0000
&
//= 0000 0000//x =x<<1;// 0000 0010for(i=0;i<8;i++)
{if((x&0x80)==0){P34_data=0; // 是0 给00,是1给1}esle{P34_data=1; // 是0 给00,是1给1}P36_SRCLK=0;P36_SRCLK=1;x=x<<1;}
P35_RCLK=0;
P35_RCLK=1;P36_SRCLK=0;
P35_RCLK=0;//发送0x02 第二行 for(i=0;i<8;i++)
{P34_data=?; // 是0 给00,是1给1P36_SRCLK=0;P36_SRCLK=1;}
P35_RCLK=0;
P35_RCLK=1;P36_SRCLK=0;
P35_RCLK=0;简化的方法:
// 1000 0000
// 1 000 0000 0for(i=0;i<8;i++)
{X=X<<1;P34_data=CY; // 是0 给00,是1给1P36_SRCLK=0;P36_SRCLK=1;}
P35_RCLK=0;
P35_RCLK=1;P36_SRCLK=0;
P35_RCLK=0;
P0=0X?
HC595(0X01)temp=0x01;
for(i=0;i<8;i++)
{P0=0X?HC595(temp) //0x01temp=temp<<1;delay();P0=0X?//,灭
}
四、 书上的代码讲解


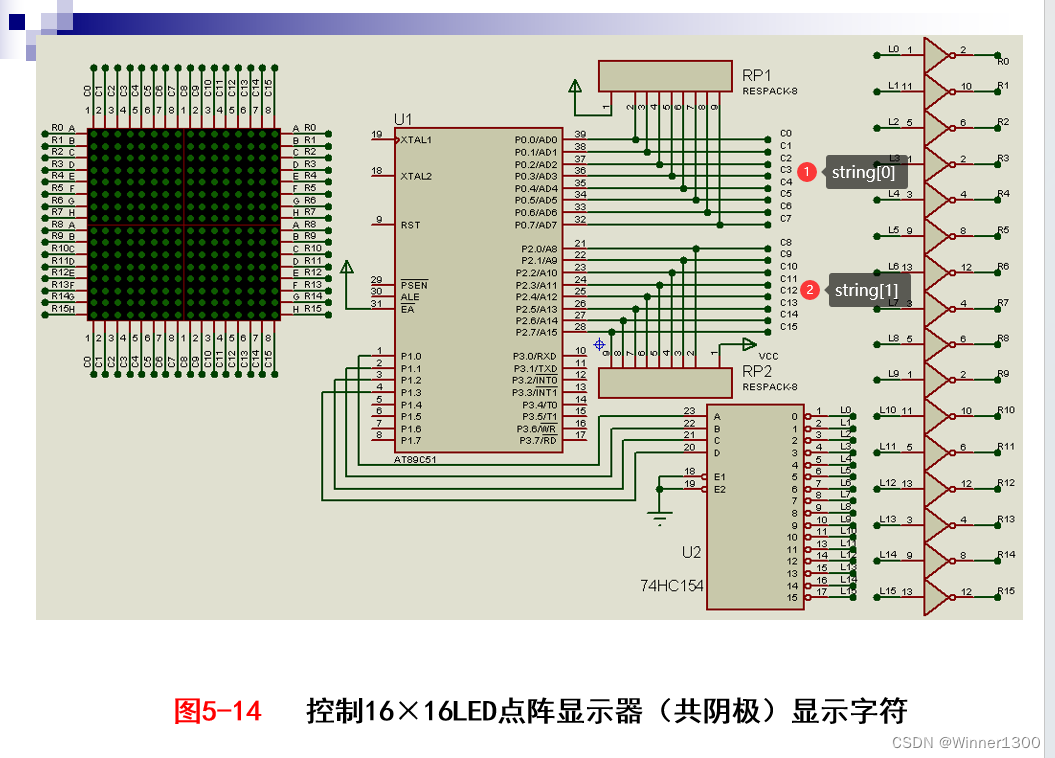
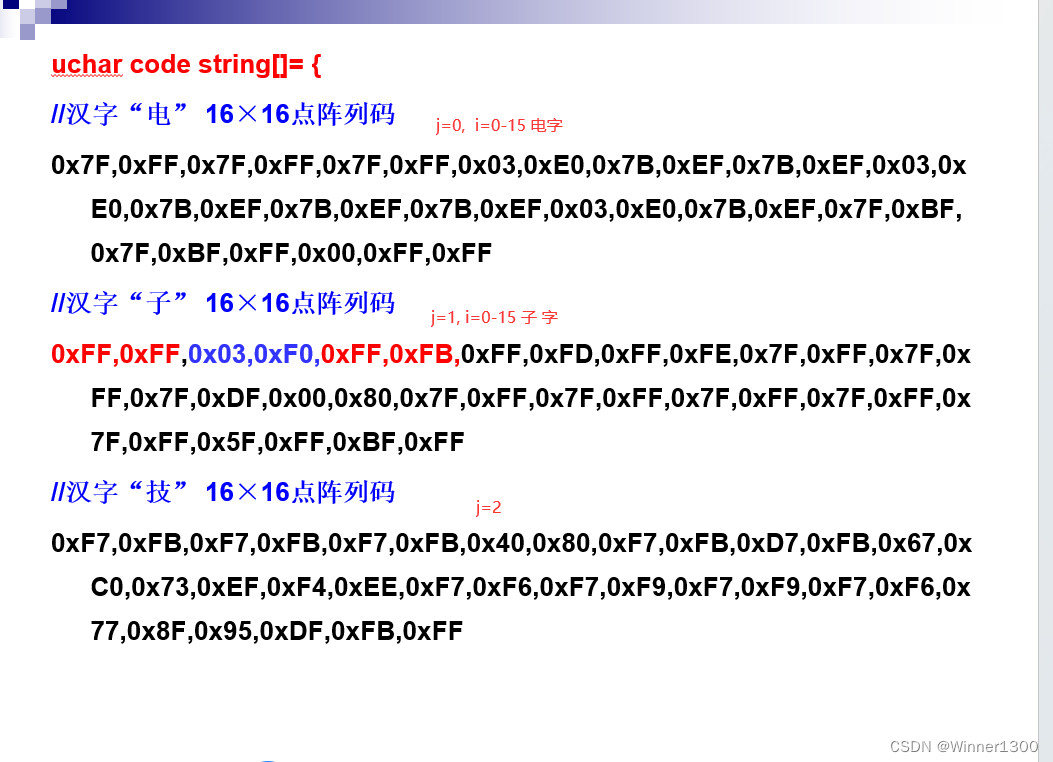
改变j显示不同的汉字,改变i显示不同行的段码;
n的讲解

总结
利用动态数码管显示的原理,用点阵显示字符。
相关文章:

51单片机点阵
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、点阵是什么?1.点阵的原理2. 3*3 点阵显示原理3. 8*8点阵实物图4. 8*8点阵内部原理图5. 16*16点阵实物图,显示原理 二、使用步骤1.先…...
远程VPN登录,IPsec,VPN,win10
windows10 完美解决L2TP无法连接问题 windows10 完美解决L2TP无法连接问题 - 哔哩哔哩...
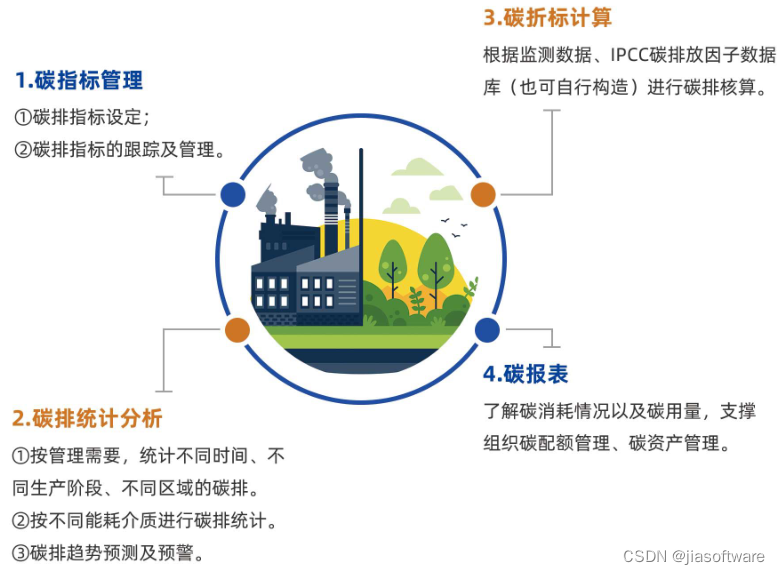
“零代码”能源管理平台:智能管理能源数据
随着能源的快速增长,有效管理和监控能源数据变得越来越重要。为了帮助企业更好的管理能源以及降低能源成本,越来越多的能源管理平台出现在市面上。 “零代码”形式的能源管理平台,采用IT与OT深度融合为理念,可进行可视化、拖拽、…...
】06 - SA8295P XBL Loader 阶段 sbl1_main_ctl 函数代码分析)
【SA8295P 源码分析 (一)】06 - SA8295P XBL Loader 阶段 sbl1_main_ctl 函数代码分析
【SA8295P 源码分析】06 - SA8295P XBL Loader 阶段 sbl1_main_ctl 函数代码分析 一、XBL Loader 汇编源码分析1.1 解析 boot\QcomPkg\XBLLoader\XBLLoader.inf1.2 boot\QcomPkg\XBLDevPrg\ModuleEntryPoint.S:跳转 sbl1_entry 函数1.3 XBLLoaderLib\sbl1_Aarch64.s:跳转 sbl…...
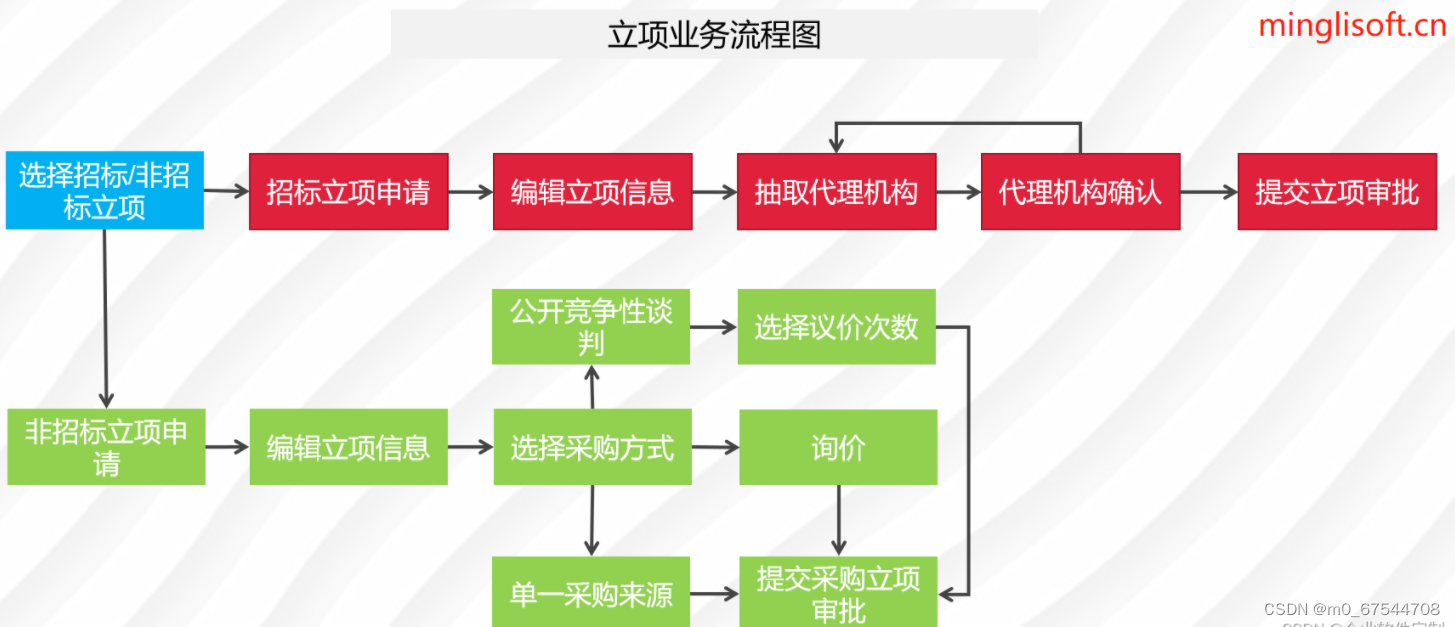
Java版本spring cloud + spring boot企业电子招投标系统源代码
项目说明 随着公司的快速发展,企业人员和经营规模不断壮大,公司对内部招采管理的提升提出了更高的要求。在企业里建立一个公平、公开、公正的采购环境,最大限度控制采购成本至关重要。符合国家电子招投标法律法规及相关规范,以及审…...

软考高级信息系统项目管理师系列论文一:论信息系统项目的整体管理
软考高级信息系统项目管理师系列论文一:论信息系统项目的整体管理 一、项目整体管理相关知识点二、摘要三、正文四、总结一、项目整体管理相关知识点 软考高级信息系统项目管理师系列之:项目整体管理...
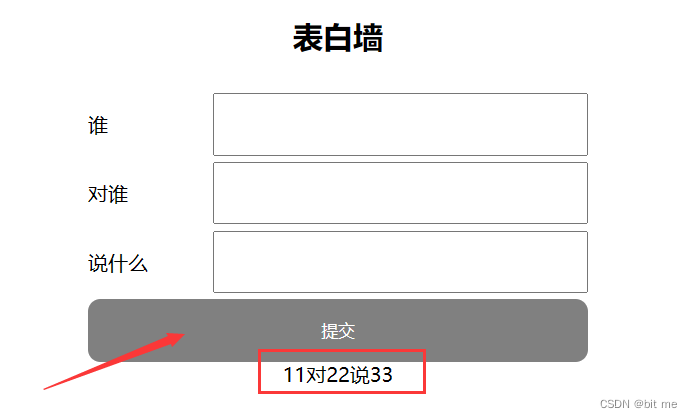
【前端】JS - WebAPI
目 录 一.WebAPI 背景知识什么是 WebAPI什么是 APIAPI 参考文档 二.DOM 基本概念什么是 DOMDOM 树 三.获取元素querySelectorquerySelectorAll 四.事件初识基本概念事件三要素 五.操作元素获取/修改元素内容(innerHTML)获取/修改元素属性获取/修改样式属…...

H5+Vue3编写官网,并打包发布到同一个域名下
背景 因为html5有利于搜索引擎抓取和收录我们网站更多的内容,对SEO很友好,可以为网站带来更多的流量,并且多端适配,兼容性和性能都非常不错,所以使用h5来编写官网首页。 因为用户个人中心可以通过官网跳转,不需要被浏…...
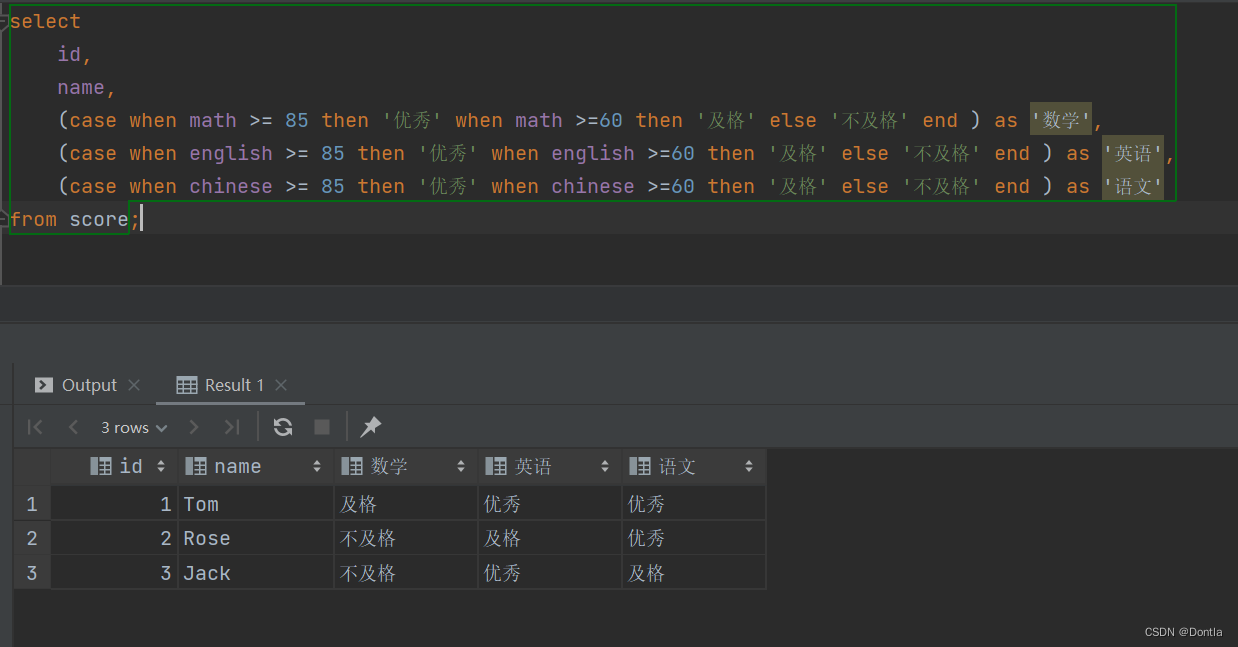
黑马mysql教程笔记(mysql8教程)基础篇——函数(字符串函数、数值函数、日期函数、流程函数)
参考文章1:https://www.bilibili.com/video/BV1Kr4y1i7ru/ 参考文章2:https://dhc.pythonanywhere.com/article/public/1/ 文章目录 基础篇函数字符串函数常用函数使用示例实例:更新已有的所有员工号,使其满足5位数长度ÿ…...

Python武器库开发-基础篇(一)
前言 以Python编程为主,围绕渗透测试展开的一门专栏。专栏内容包括: Python基础编程(Python基础、语法、对象、文件操作,错误和异常),Python高级编程(正则表达式、网络编程、WEB编程࿰…...
Qt (QFileDialogQColorDialogQFontDialog) 对话框实战
目录 一、QFileDialog 类 (文件对话框) 二、QColorDialog 类(颜色对话框) 三、QFontDialog 类(字体对话框类) 一、QFileDialog 类 (文件对话框) QFileDialog 是 Qt 框架中的一个类,用于在应用程序中提供文件对话框。它允许用户选择文件或目录,并且可…...

2.SpringSecurity - 处理器简单说明
文章目录 SpringSecurity 返回json一、登录成功处理器1.1 统一响应类HttpResult1.2 登录成功处理器1.3 配置登录成功处理器1.4 登录 二、登录失败处理器2.1 登录失败处理器2.2 配置登录失败处理器2.3 登录 三、退出成功处理器3.1 退出成功处理器3.2 配置退出成功处理器3.3 退出…...
AGI热门方向:国内前五!AI智能体TARS-RPA-Agent落地,实在智能打造人手一个智能助理
早在 1950 年代,Alan Turing 就将「智能」的概念扩展到了人工实体,并提出了著名的图灵测试。这些人工智能实体通常被称为 —— 代理(Agent)。 代理这一概念起源于哲学,描述了一种拥有欲望、信念、意图以及采取行动能力…...

运动品牌如何做到“全都要”?来看看安踏的答案
文 | 螳螂观察 作者 | 易不二 运动鞋服是兼具高景气和清晰格局的优质消费赛道。 中信证券给出的这一预测,欧睿国际也做出了更具体的测算:预计到2027年,中国运动服饰市场规模有望以约为8.7%的年复合增长率,突破5500亿元人民币。…...

LeetCode75——Day6
文章目录 一、题目二、题解 一、题目 151. Reverse Words in a String Given an input string s, reverse the order of the words. A word is defined as a sequence of non-space characters. The words in s will be separated by at least one space. Return a string …...

http代理有什么好处,怎么通过http代理服务安全上网呢?
通过http代理上网是一种常见的网络代理方式。http代理是指通过代理服务器进行网络连接,以实现隐藏自己的真实IP地址、保护个人隐私等目的。下面我们将介绍通过http代理上网的好处以及如何使用http代理服务来安全上网。 一、通过http代理上网的好处 1. 保护个人隐私 …...
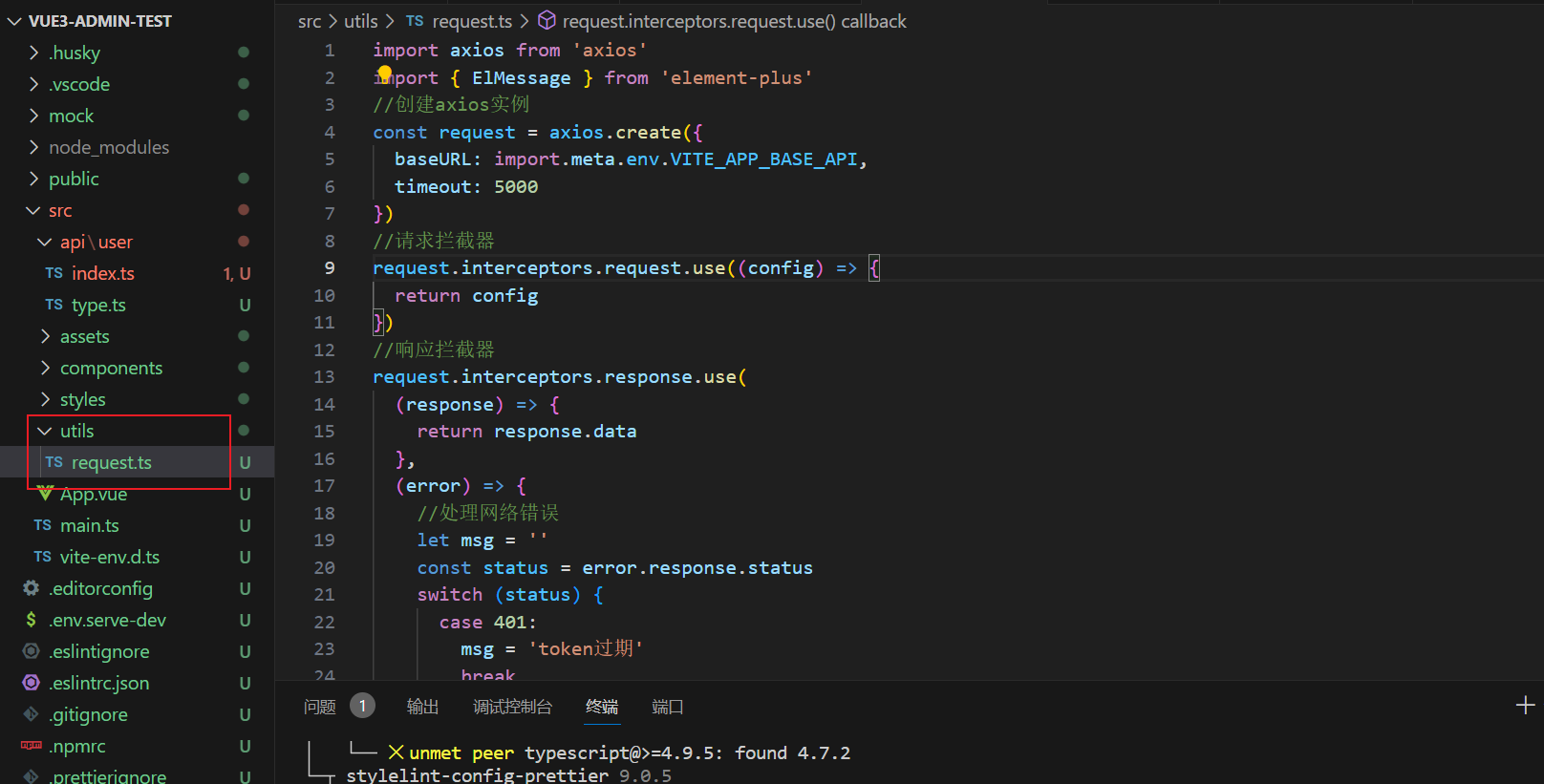
vue3后台管理框架之axios二次封装
在开发项目的时候避免不了与后端进行交互,因此我们需要使用axios插件实现发送网络请求。在开发项目的时候 我们经常会把axios进行二次封装。 目的: 1:使用请求拦截器,可以在请求拦截器中处理一些业务(开始进度条、请求头携带公共参数) 2:使用响应拦截器…...
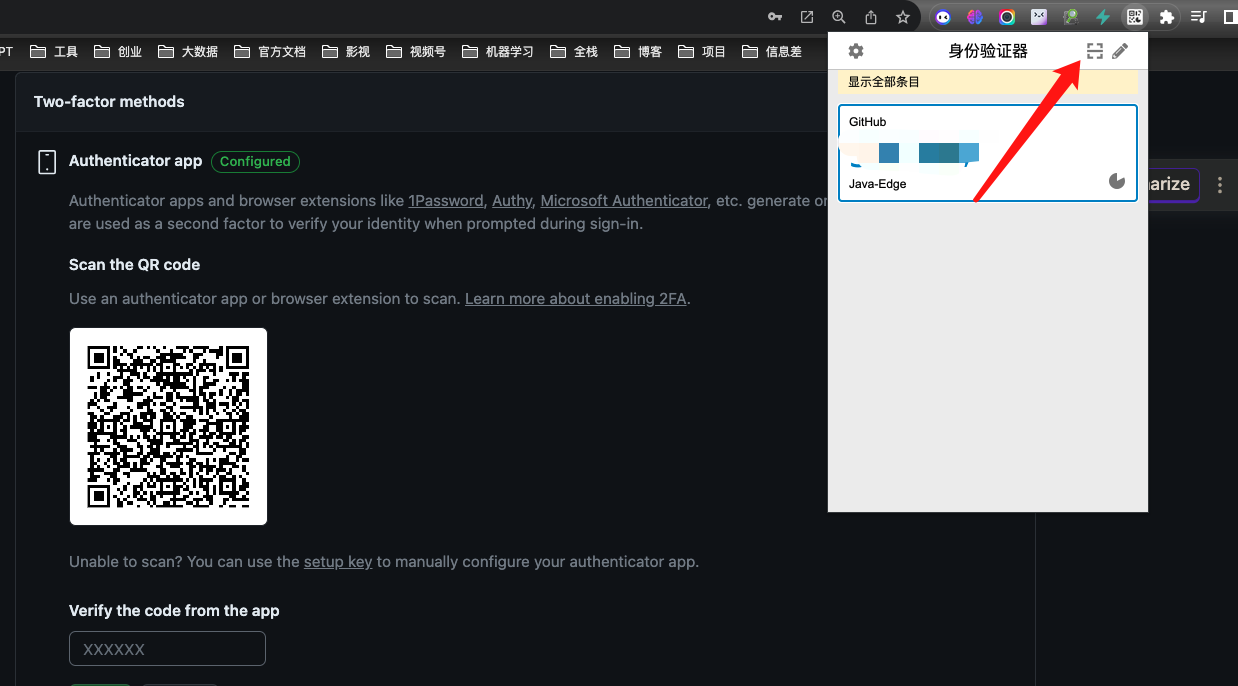
你的Github账户可能被封禁!教你应对Github最新的2FA二次验证! 无地区限制, 无额外设备的全网最完美方案
1 2FA 的定义 双因素身份验证 (2FA) 是一种身份和访管理安全方法,需要经过两种形式的身份验证才能访河资源和数据,2FA使企业能够监视和帮助保护其最易受攻击的信息和网络。 2 2FA 的身份验证方法 使用双因素身份验证时有不同的身份验证方法。此处列出…...

【C语言】#define宏与函数的优劣对比
本篇文章目录 1. 预处理指令#define宏2. #define定义标识符或宏,要不要最后加上分号?3.宏的参数替换后产生的运算符优先级问题3.1 问题产生3.2 不太完美的解决办法3.3 完美的解决办法 4.#define的替换规则5. 有副作用的宏参数6. 宏与函数的优劣对比6.1 宏…...

flask基础开发知识学习
之前做了一些LLM的demo,接口用flask写的,但是涉及到后端的一些业务就感觉逻辑写的很乱,代码变成屎山,于是借助官方文档和GPT迅速补了一些知识,总结一下一个很小的模板 于是决定边学边重构之前的代码… 文章目录 代码结…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
