深入理解强化学习——智能体的类型:有模型强化学习智能体与免模型强化学习智能体
分类目录:《深入理解强化学习》总目录
根据智能体学习的事物不同,我们可以把智能体进行归类。基于价值的智能体(Value-based agent)显式地学习价值函数,隐式地学习它的策略。策略是其从学到的价值函数里面推算出来的。基于策略的智能体(Policy-based Agent)直接学习策略,我们给它一个状态,它就会输出对应动作的概率。基于策略的智能体并没有学习价值函数。把基于价值的智能体和基于策略的智能体结合起来就有了Actor-Critic智能体(Actor-Critic Agent)。这一类智能体把策略和价值函数都学习了,然后通过两者的交互得到最佳的动作。本文就将介绍有模型强化学习智能体和免模型强化学习智能体的区别。
我们可以通过智能体到底有没有学习环境模型来对智能体进行分类。 有模型(Model-based)强化学习智能体通过学习状态的转移来采取动作。 免模型(Model-free)强化学习智能体没有去直接估计状态的转移,也没有得到环境的具体转移变量,它通过学习价值函数和策略函数进行决策。免模型强化学习智能体的模型里面没有环境转移的模型。
我们可以用马尔可夫决策过程来定义强化学习任务,并将其表示为四元组 < S , A , P , R > <S, A, P, R> <S,A,P,R>,即状态集合、动作集合、状态转移函数和奖励函数。如果这个四元组中所有元素均已知,且状态集合和动作集合在有限步数内是有限集,则智能体可以对真实环境进行建模,构建一个虚拟世界来模拟真实环境中的状态和交互反应。 具体来说,当智能体知道状态转移函数 P ( s t + 1 ∣ s t , a t ) P(s_{t+1}|s_t, a_t) P(st+1∣st,at)和奖励函数 R ( s t , a t ) R(s_t, a_t) R(st,at)后,它就能知道在某一状态下执行某一动作后能带来的奖励和环境的下一状态,这样智能体就不需要在真实环境中采取动作,直接在虚拟世界中学习和规划策略即可。这种学习方法称为有模型强化学习。 有模型强化学习的流程如下图所示:
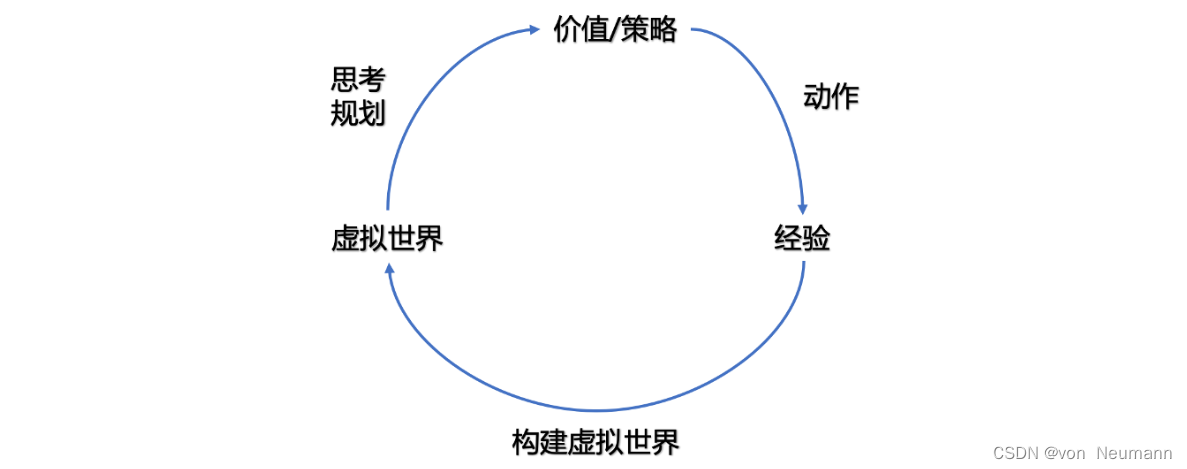
然而在实际应用中,智能体并不是那么容易就能知道马尔可夫决策过程中的所有元素的。通常情况下,状态转移函数和奖励函数很难估计,甚至连环境中的状态都可能是未知的,这时就需要采用免模型强化学习。免模型强化学习没有对真实环境进行建模,智能体只能在真实环境中通过一定的策略来执行动作,等待奖励和状态迁移,然后根据这些反馈信息来更新动作策略,这样反复迭代直到学习到最优策略。
针对是否需要对真实环境建模,强化学习可以分为有模型强化学习和免模型强化学习。有模型强化学习是指根据环境中的经验,构建一个虚拟世界,同时在真实环境和虚拟世界中学习;免模型强化学习是指不对环境进行建模,直接与真实环境进行交互来学习到最优策略。
总之,有模型强化学习相比免模型强化学习仅仅多出一个步骤,即对真实环境进行建模。因此,一些有模型的强化学习方法,也可以在免模型的强化学习方法中使用。在实际应用中,如果不清楚该用有模型强化学习还是免模型强化学习,可以先思考在智能体执行动作前,是否能对下一步的状态和奖励进行预测,如果能,就能够对环境进行建模,从而采用有模型学习。
免模型强化学习通常属于数据驱动型方法,需要大量的采样来估计状态、动作及奖励函数,从而优化动作策略。例如,在雅达利平台上的《太空侵略者》游戏中,免模型的深度强化学习需要大约两亿帧游戏画面才能学到比较理想的效果。相比之下,有模型的深度强化学习可以在一定程度上缓解训练数据匮乏的问题,因为智能体可以在虚拟世界中进行训练。 免模型学习的泛化性要优于有模型强化学习,原因是有模型强化学习算需要对真实环境进行建模,并且虚拟世界与真实环境之间可能还有差异,这限制了有模型强化学习算法的泛化性。 有模型的强化学习方法可以对环境建模,使得该类方法具有独特魅力,即“想象能力”。在免模型强化学习中,智能体只能一步一步地采取策略,等待真实环境的反馈;有模型强化学习可以在虚拟世界中预测出将要发生的事,并采取对自己最有利的策略。
目前,大部分深度强化学习方法都采用了免模型强化学习,这是因为:免模型强化学习更为简单、直观且有丰富的开源资料,如AlphaGo系列都采用免模型强化学习;在目前的强化学习研究中,大部分情况下环境都是静态的、可描述的,智能体的状态是离散的、可观察的(如雅达利游戏平台),这种相对简单、确定的问题并不需要评估状态转移函数和奖励函数,可直接采用免模型强化学习,使用大量的样本进行训练就能获得较好的效果。
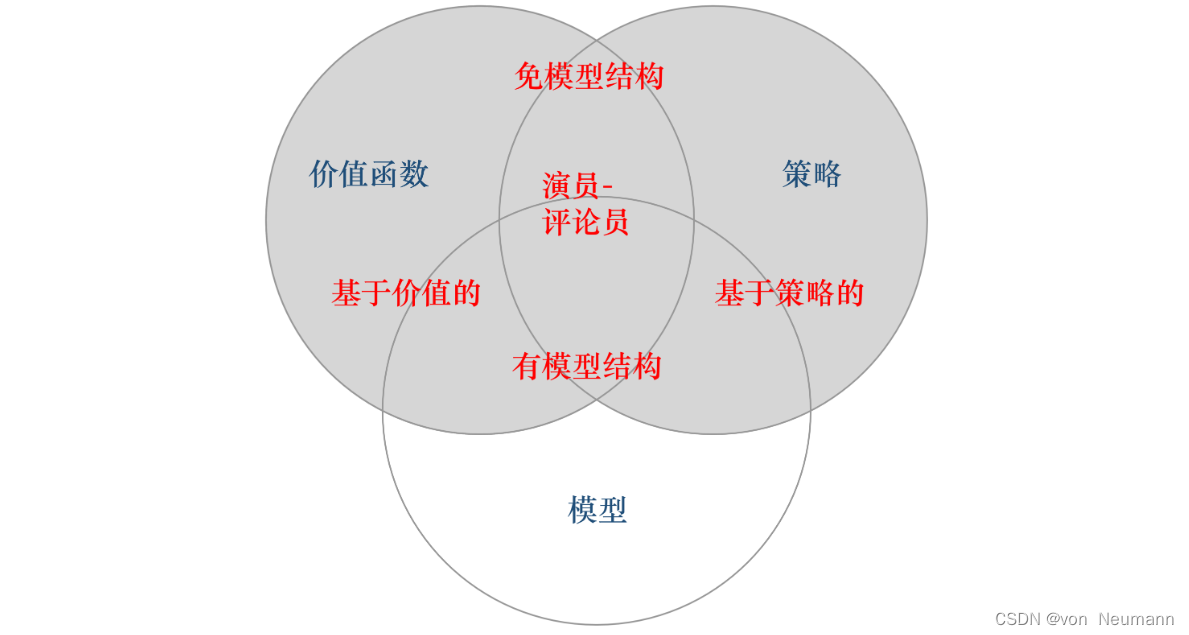
如下图所示,我们可以把几类模型放到同一个图里面。下图有3个组成成分:价值函数、策略和模型。按一个智能体具有三者中的三者、两者或一者的情况可以把它分成很多类:
参考文献:
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习(第2版)[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践(原书第2版)[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL:强化学习教程 [M]. 人民邮电出版社, 2022
相关文章:

深入理解强化学习——智能体的类型:有模型强化学习智能体与免模型强化学习智能体
分类目录:《深入理解强化学习》总目录 根据智能体学习的事物不同,我们可以把智能体进行归类。基于价值的智能体(Value-based agent)显式地学习价值函数,隐式地学习它的策略。策略是其从学到的价值函数里面推算出来的。…...
vue项目获得开源代码之后跳过登录界面
readme运行 进入到账号和密码 找到main.js 比如说,以上这段代码 剩下next()就成功进入了...
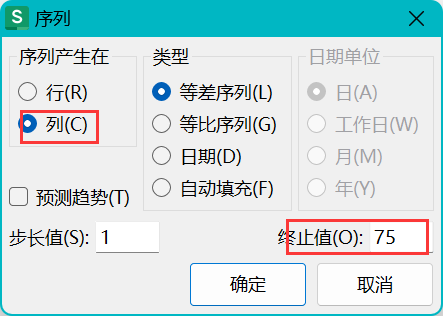
WPS、Excel表格增加一列,序列1到任意大小 / 填充某个范围的数字到列
Excel添加一列递增的数字方法有如下: 一、最常用的,使用鼠标放到右下角下拉增加 1、选中起始框的右下角,直到显示黑色实心十字 2、一直向下拖动 3、成功 这种填充方式是最常用的,100以内都可以轻松瞬间完成 1~100填充 但是如果…...
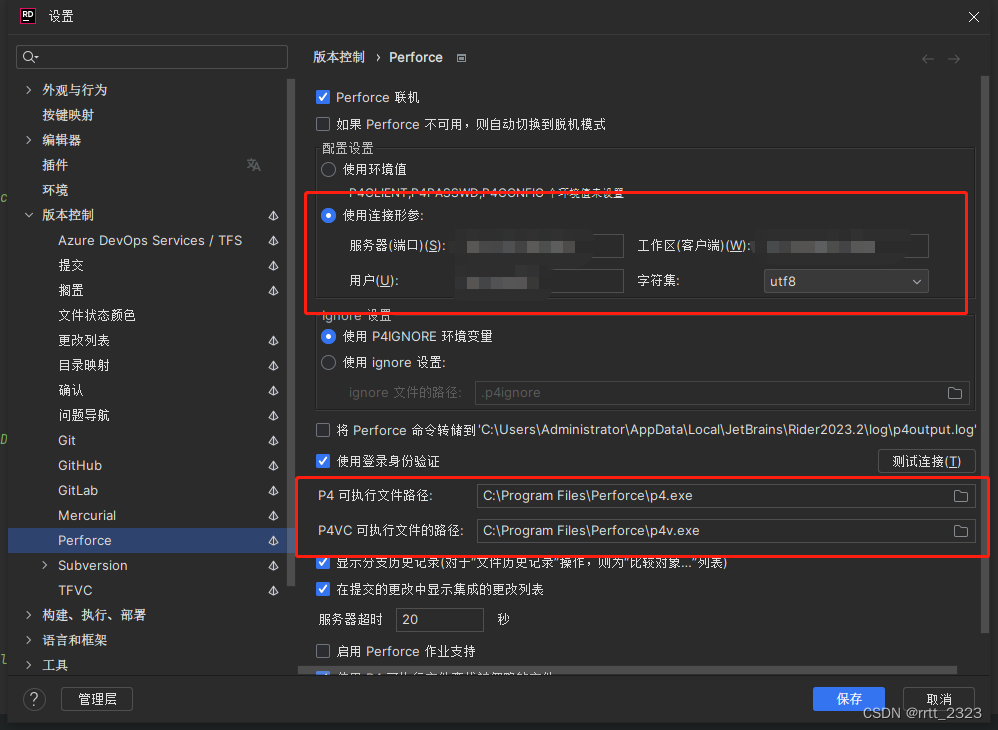
在 rider 里用配置 Perforce(P4)的注意事项
整个配置界面里,关键就配2处位置,但是都有些误导性。 1是连接形参的4个参数都得填,字符集看你项目的要求,这里工作区其实指的是你的工作空间,还不如显示英文的 Workspace 呢,搞得我一开始没填,…...
)
在Spring中,标签管理的Bean中,为什么使用@Autowired自动装配修饰引用类(前提条件该引用类也是标签管理的Bean)
Autowired是Spring框架的一个注解,它可以用来完成自动装配。 自动装配是Spring框架的一个特性,它可以避免手动去注入依赖,而是由框架自动注入。这样可以减少代码的重复性和提高开发效率。 在使用Autowired注解时,Spring会自动搜…...

俄罗斯YandexGPT 2在国家考试中获得高分;OpenAI API开发者快速入门指南
🦉 AI新闻 🚀 俄罗斯YandexGPT 2聊天机器人成功在国家考试中获得高分 摘要:俄罗斯YandexGPT 2聊天机器人通过国家统一考试文学科目,以55分的加权分数成功进入大学。Yandex团队强调他们在开发过程中确保数据库不包含任何关于统考…...

Nginx 同一端口下部署多个 Vue3 项目
前言 前端多项目部署到 Nginx 的同一监听端口下的解决方案,项目由一个主项目和多个子项目组成,主项目和子项目都是单独打包。 主子项目之间是使用的腾讯开源的无界(WebComponent 容器 iframe 沙箱)前端框架,能够完善…...
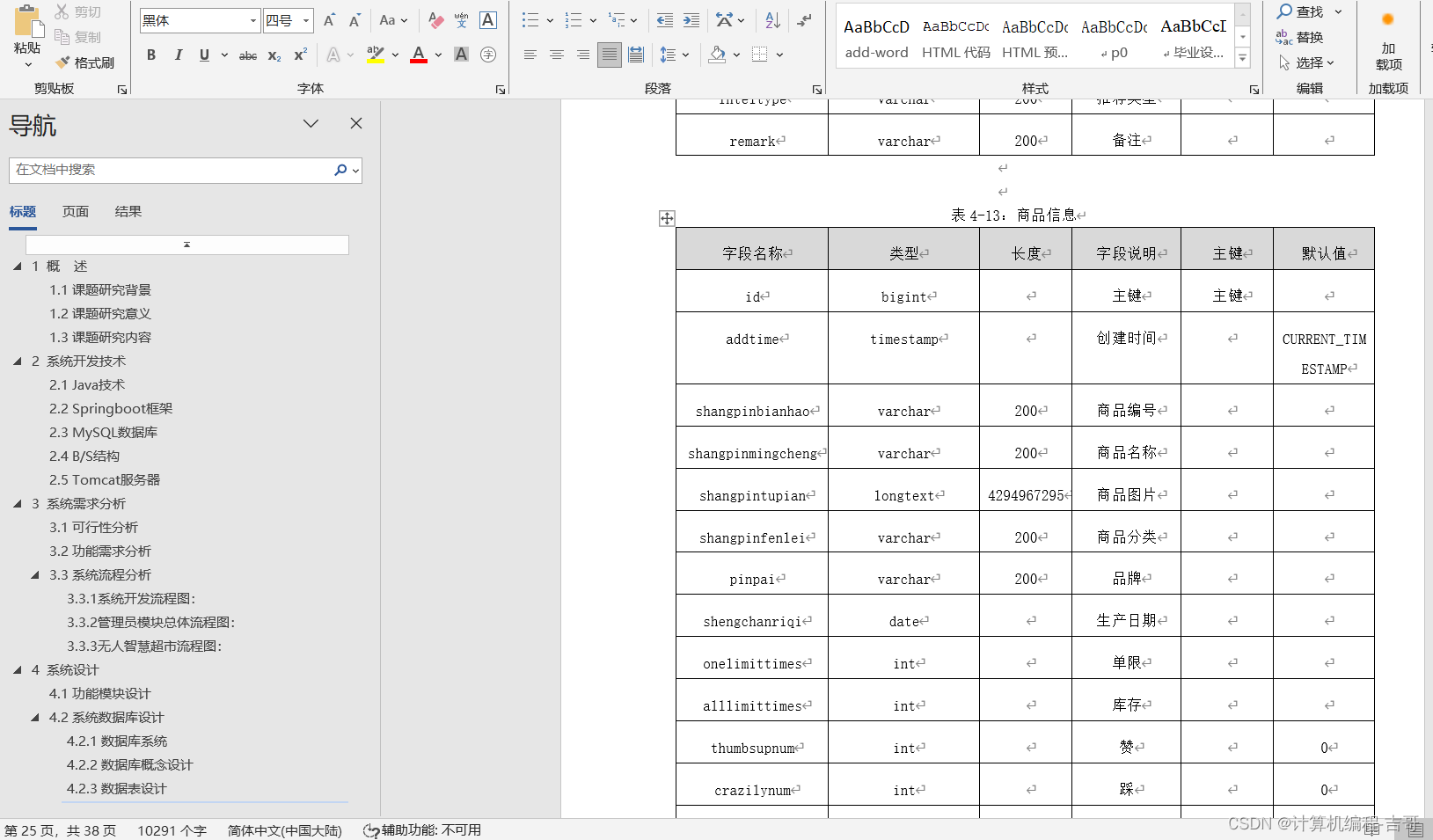
计算机毕业设计 无人智慧超市管理系统的设计与实现 Javaweb项目 Java实战项目 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

js构造函数和原型链
以下是一个简单的JS原型链代码示例: function Person(name, age) {this.name name;this.age age; }Person.prototype.sayHello function() {console.log(Hello, Im ${this.name} and Im ${this.age} years old.); }let person1 new Person(Alice, 20);person1.…...
矩阵和array()数组(待完善))
python中matrix()矩阵和array()数组(待完善)
参考:python矩阵中matrix()和array()函数区别-CSDN博客 区别: 维度:ndarray可以是多维的,包括1D、2D、3D等,而matrix只能是2维的,也就是矩阵。数据类型:ndarray的数据类型可以不一致…...
设计海报都有哪些好用的软件推荐
在新媒体时代,设计在各个方面都是不可分割的。它最初是设计师的工作,并逐渐成为新媒体编辑的必要技能。 网页内容需要图片和文字,应用程序需要独特的风格基调,人们更喜欢分享视频和图片,而不是简单的文本。因此&#…...
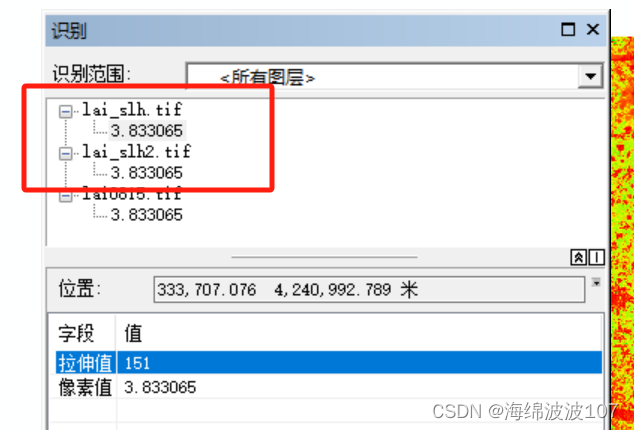
Arcgis中像元值变化问题,拉伸显示的是否为实际像元值范围?
Arcgis中合并栅格但像元值变化 问题描述 这是四幅栅格,范围都在-1-9之间,怀疑这个范围是否是真实的范围。因为经常听到同学说放到arcgis拉伸显示之后,值变化了,所以研究一下。 原因 可以打开ENVI的像元快速统计工具ÿ…...
oracle库中数据利用datax工具同步至mysql库
查看oracle版本 $sqlplus aaa/aaaa192.168.1.1/lcfaSQL*Plus: Release 19.0.0.0.0 - Production on Tue Oct 17 15:56:46 2023 Version 19.15.0.0.0Copyright (c) 1982, 2022, Oracle. All rights reserved.Last Successful login time: Tue Oct 17 2023 15:56:03 08:00Conne…...
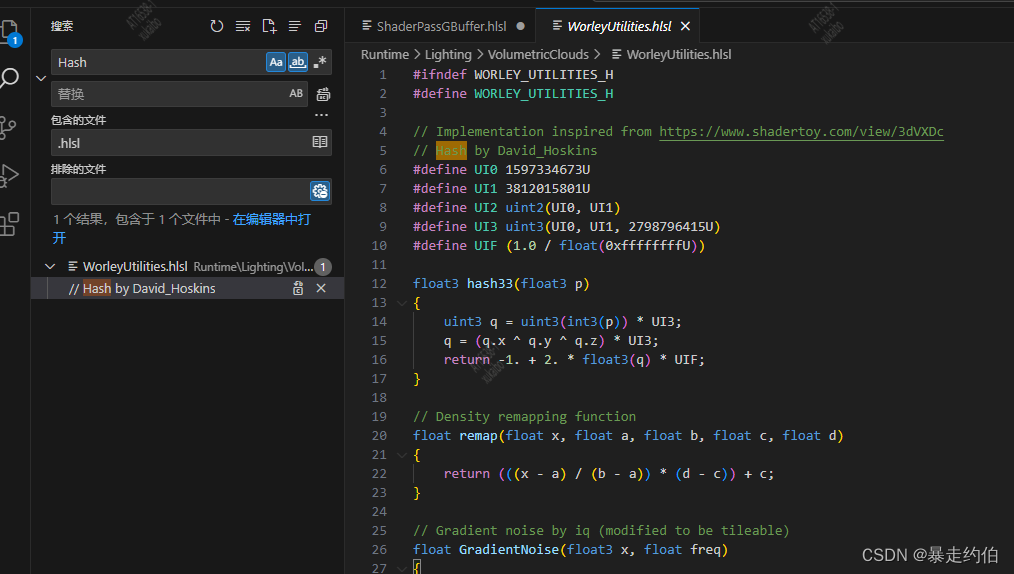
【Unity HDRP渲染管线下的WorleyUtilities文件,“Hash”函数】
Unity HDRP内置文件WorleyUtilities WorleyUtilities文件路径如下:文件代码如下然后转译到ShaderLab中:存档:WorleyUtilities文件路径如下: D:…\Library\PackageCache\com.unity.render-pipelines.high-definition@14.0.8\Runtime\Lighting\VolumetricClouds\WorleyUtili…...

前端跨域问题解决
一、同源策略 同源策略是一个重要的安全策略,它用于限制一个Origin的文档或者它加载的脚本如何能与另一个源的资源进行交互。它能帮助阻隔恶意文档,减少可能被攻击的媒介。 Origin:指web文档的来源,Web 内容的来源取决于访问的U…...
【前端】Js
目 录 一.前置知识第一个程序JavaScript 的书写形式注释输入输出 二.语法概览变量的使用理解 动态类型基本数据类型 三.运算符算术运算符赋值运算符 & 复合赋值运算符自增自减运算符比较运算符逻辑运算符位运算移位运算 四.条件语句if 语句三元表达式switch 五.循环语句whi…...
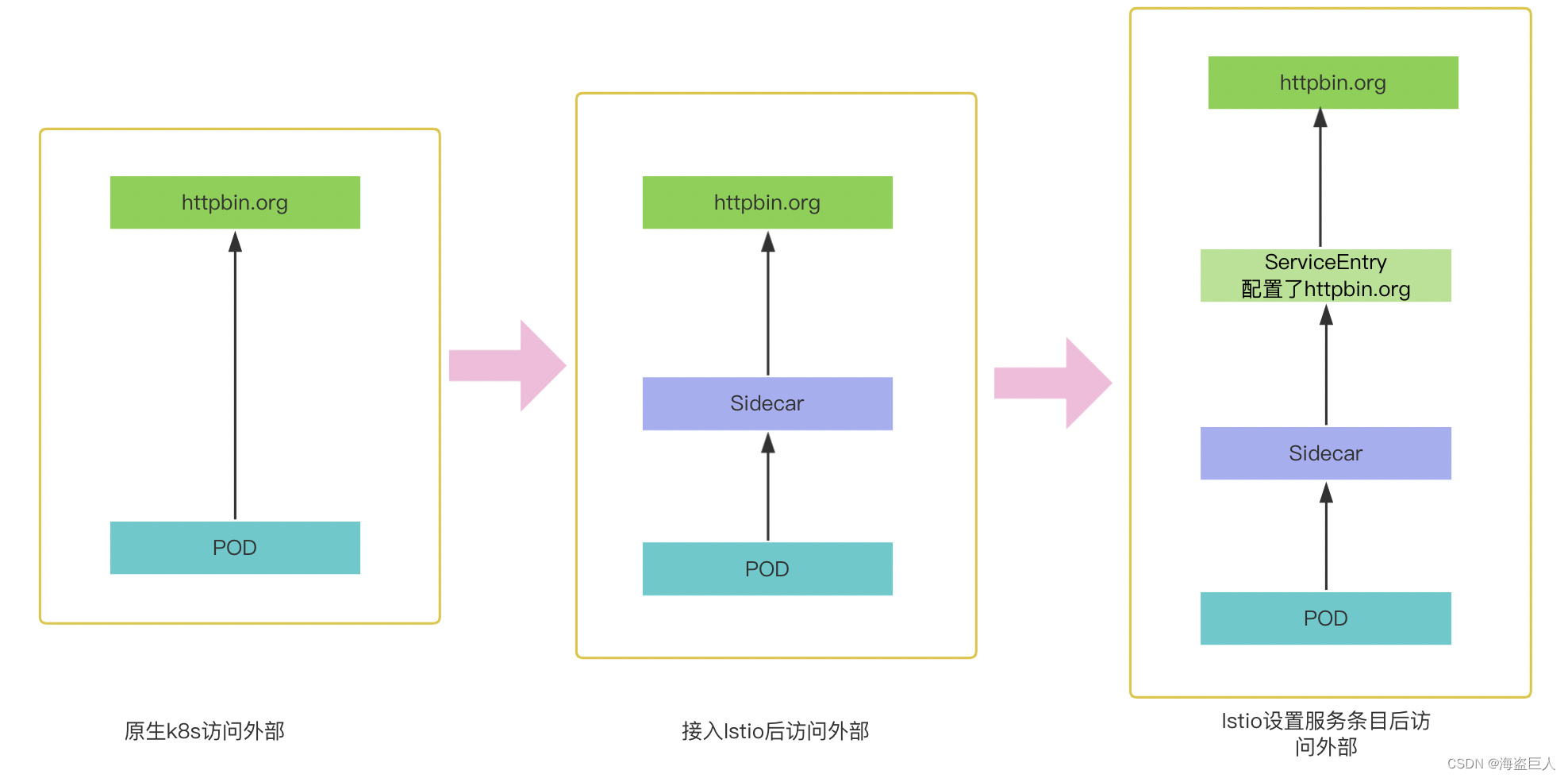
第四章 Istio出口流量管理
文章目录 访问外部服务Envoy 代理将请求传递给网格外服务配置服务条目以提供对外部服务的受控访问访问外部 HTTP 服务 直接访问外部服务 出口网关清理 HTTP 网关其他 访问外部服务 为了更好的做好网络访问控制,k8s结合Istio出口网络升级示意图 来自 Istio 的 pod…...

leetcode做题笔记188. 买卖股票的最佳时机 IV
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。 注意:你不能同时参与多…...
基于springboot实现大学生社团活动平台项目【项目源码+论文说明】
摘要 21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,网络管理工作的重要性已逐渐被人们所认识,科学化的管理,使信…...

力扣--第三大的数
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。 示例 1: 输入:[3, 2, 1] 输出:1 解释:第三大的数是 1 。 示例 2: 输入:[1, 2] 输出࿱…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
