leetcode做题笔记188. 买卖股票的最佳时机 IV
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3] 输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
思路一:动态规划
c解法
int maxProfit(int k, int* prices, int pricesSize) {int n = pricesSize;if (n == 0) {return 0;}k = fmin(k, n / 2);int buy[n][k + 1], sell[n][k + 1];memset(buy, 0, sizeof(buy));memset(sell, 0, sizeof(sell));buy[0][0] = -prices[0];sell[0][0] = 0;for (int i = 1; i <= k; ++i) {buy[0][i] = sell[0][i] = INT_MIN / 2;}for (int i = 1; i < n; ++i) {buy[i][0] = fmax(buy[i - 1][0], sell[i - 1][0] - prices[i]);for (int j = 1; j <= k; ++j) {buy[i][j] = fmax(buy[i - 1][j], sell[i - 1][j] - prices[i]);sell[i][j] = fmax(sell[i - 1][j], buy[i - 1][j - 1] + prices[i]);}}int ret = 0;for (int i = 0; i <= k; i++) {ret = fmax(ret, sell[n - 1][i]);}return ret;
}分析:
本题为买卖股票例题,利用动态规划即可解决,题目中要求买k次卖k次所能赚得的最大数,状态方程则要考虑买卖k次的情况,所以 buy[i][j] = fmax(buy[i - 1][j], sell[i - 1][j] - prices[i]);循环k次判断前k次中怎样使利润最大,最后返回数组内最大值即可
总结:
本题考察动态规划的应用,判断k次后得到每次交易后所能得到的最大利润,最后返回最大值即可解决
相关文章:

leetcode做题笔记188. 买卖股票的最佳时机 IV
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。 注意:你不能同时参与多…...
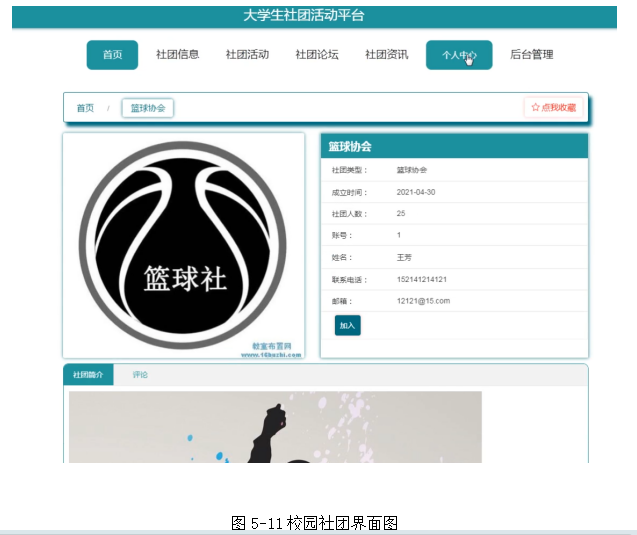
基于springboot实现大学生社团活动平台项目【项目源码+论文说明】
摘要 21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,网络管理工作的重要性已逐渐被人们所认识,科学化的管理,使信…...

力扣--第三大的数
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。 示例 1: 输入:[3, 2, 1] 输出:1 解释:第三大的数是 1 。 示例 2: 输入:[1, 2] 输出࿱…...

Android 11.0 禁用adb reboot recovery命令实现正常重启功能
1.前言 在11.0的系统开发中,在定制recovery模块的时候,由于产品开发需要要求禁用recovery的相关功能,比如在通过adb命令的 adb reboot recovery的方式进入recovery也需要实现禁用,所以就需要了解相关进入recovery流程来禁用该功能 2.禁用adb reboot recovery命令实现正常…...

Cesium Vue(一)— 项目初始化配置
1. 创建VUE项目工程 创建项目 vue create cesium-vue配置Vue3 2. 创建vue.config.js文件 const { defineConfig } require(vue/cli-service)// The path to the CesiumJS source code const cesiumSource node_modules/cesium/Source; const cesiumWorkers ../Build/C…...
】)
【linux下centos7.9安装docker,docker-composed(root用户)】
一 安装docker 1.联网下载安装docker curl -fsSL https://get.docker.com | bash -s docker --mirror Aliyun 2.安装成功 docker -v 3.将docker注册为service,进入/etc/systemd/system/目录,并创建docker.service文件(注意insecure-registry修改成自己的…...
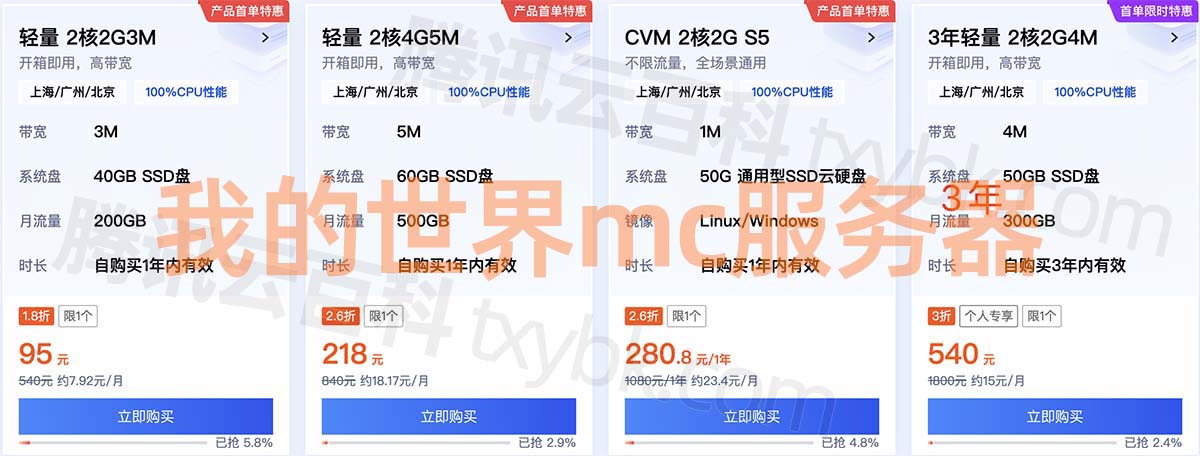
腾讯云我的世界mc服务器配置怎么选择?
使用腾讯云服务器开Minecraft我的世界服务器配置怎么选择?10人以内玩2核4G就够用了,开我的世界服务器选择轻量应用服务器就够了,腾讯云轻量CPU采用至强白金处理器,大型整合包一般1.12版本的,轻量2核4G配置都差不多的&a…...
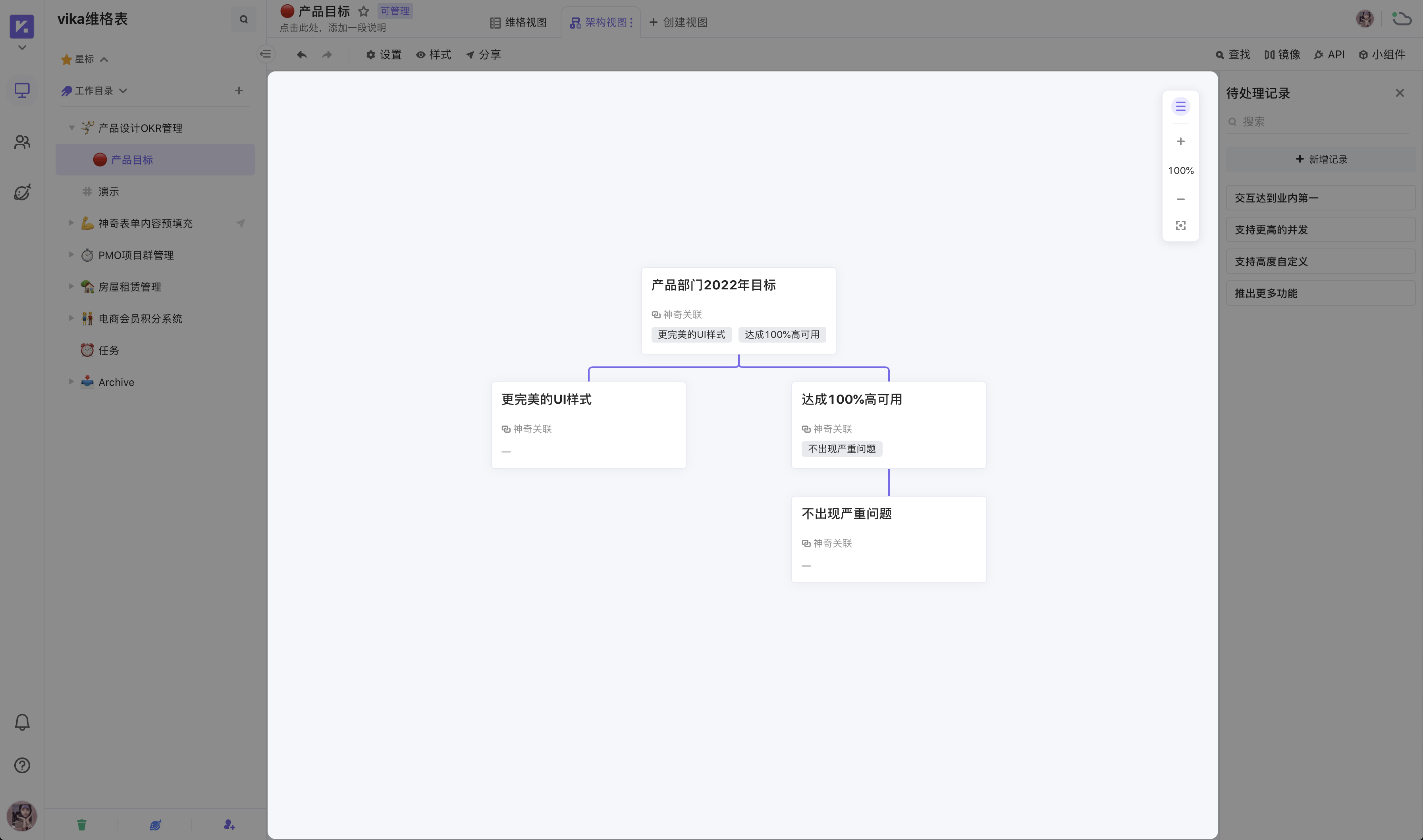
《低代码指南》——AI低代码维格云架构视图怎么用?
架构视图是一个展示信息层级关系的视图,轻轻拖拽卡片,就能搭建精巧缜密的企业组织架构视图、实现信息结构化。 利用好架构视图,可以很好地解决以下场景: 展示企业/团队的组织关系 可视化管理产品开发架构 统筹全员 OKR 完成情况 架构视图的基础知识 架构视图分为以下几个…...
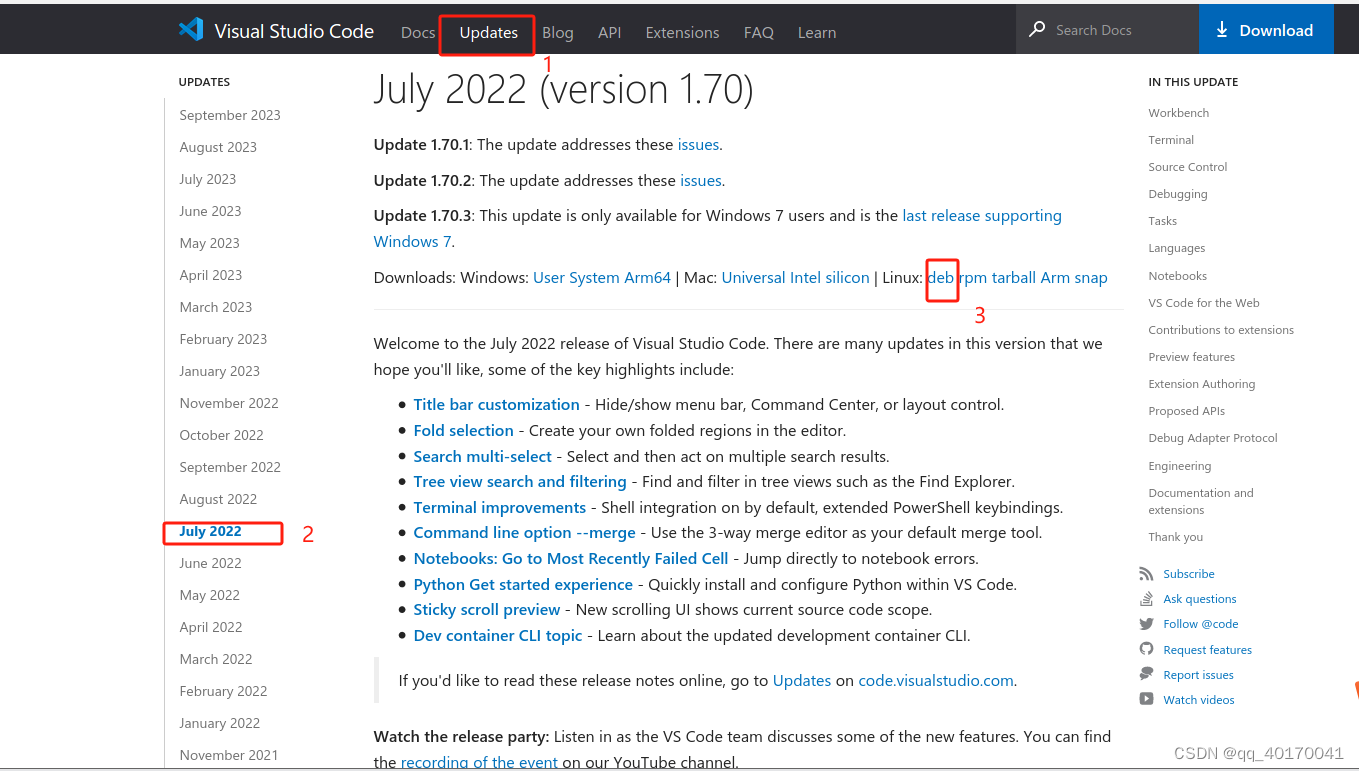
ubuntu16.04安装vscode遇到的code 依赖于 libnss3 (>= 2:3.30)解决
ubuntu16.04安装vscode遇到的code 依赖于 libnss3 (> 2:3.30);然而:系统中 libnss3:amd64 的版本为 2:3.28.4-0ubuntu0.16.04.14解决方法 一开始下载了最新版本的vscode,安装时出现了上面的错误状况,最新版本的依赖库版本过低的…...
它来了,xhadmin多应用Saas框架正式发布!
这是一个很激动人心的时刻,因为这个框架从立项到现在已经一年多的时间了,先给大家欣赏下颜值吧。 上图所示是总后台的首页截图,看上去还是比较满意的,不过后续还有一些小小的调整。 应用市场的效果也是相当炸裂的,整体…...

PixMIM论文笔记
论文名称:PixMIM: Rethinking Pixel Reconstruction in Masked Image Modeling 发表时间:2023 年 3 月 4 日 作者及组织:上海人工智能实验室、西蒙菲莎大学、香港中文大学 GitHub:https://github.com/open-mmlab/mmselfsup/tree/d…...
设计师首选:最佳的5款网页设计软件
对于UI设计师来说,网页设计是一项必要的技能。如何做好网页设计?除了设计理念,网页设计和制作软件的应用也是不可或缺的。目前市场上有很多这样的软件,工人要想做好,就必须先磨利工具。如果他们想做网页设计࿰…...

ES6箭头函数
1.箭头函数的写法 如果函数内有返回值 var fn v > v 1 返回值如果不是表达式(是对象),用()括号返回 var fn v > ({ obj: v }) 返回值如果不是表达式(也不是对象)方法体内按正常写 var fu () > {var a 1;var b a1;return b; } 2.箭头函数和普通…...

毫米波雷达在环境监测中的关键作用
随着环境问题的日益凸显,精确、实时的环境监测成为了保护地球的关键一环。在这个背景下,毫米波雷达技术逐渐崭露头角,以其在环境监测中的独特优势成为不可或缺的工具。本文将探讨毫米波雷达在环境监测中的关键作用,以及它是如何应…...
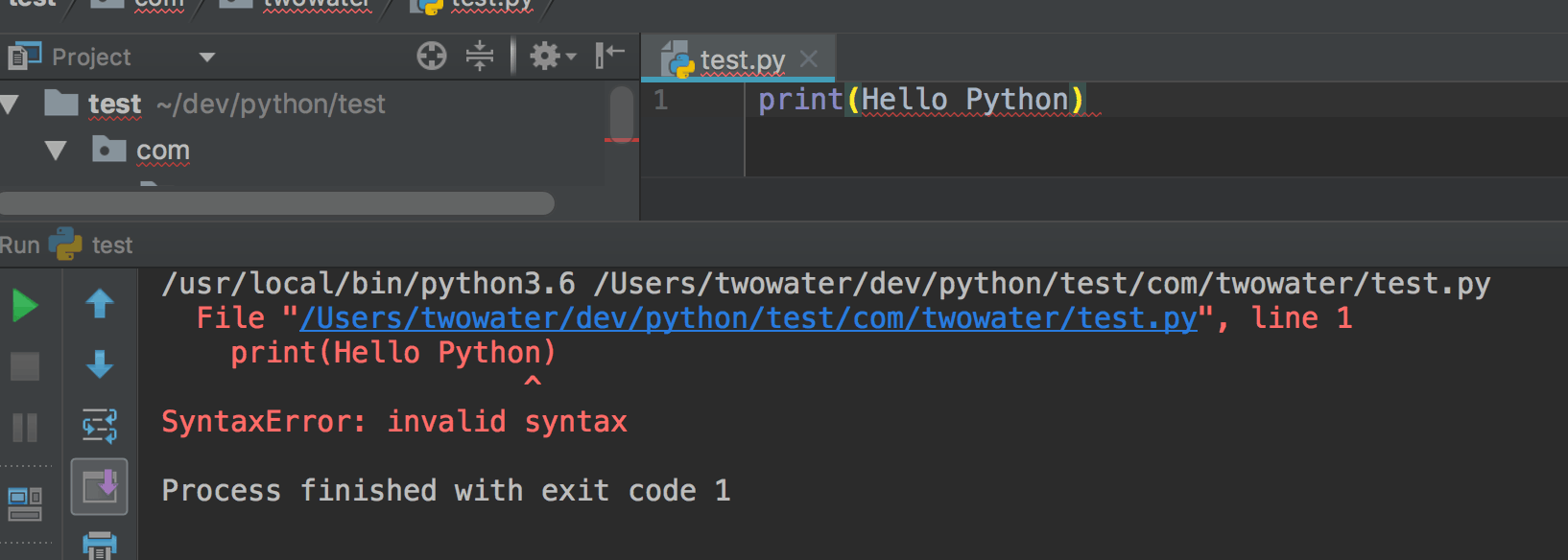
print() 函数
二、print() 函数 这里先说一下 print() 函数,如果你是新手,可能对函数不太了解,没关系,在这里你只要了解它的组成部分和作用就可以了,后面函数这一块会详细说明的。 print() 函数由两部分构成 : 指令&a…...
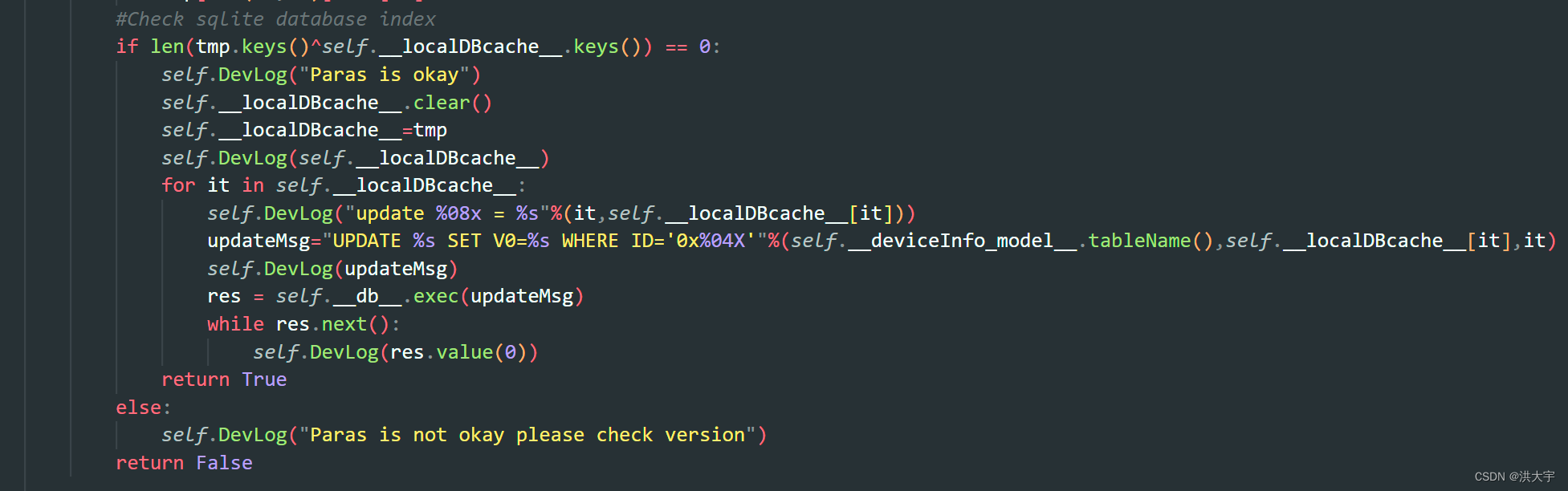
PyQt 小程序
设备管理程序 v0.0.1.0, 终于出了一个基础版本,… … 两个字典的键值判断 辛亏用的是Python 这个编码时间大大缩短了...

大模型技术实践(五)|支持千亿参数模型训练的分布式并行框架
在上一期的大模型技术实践中,我们介绍了增加式方法、选择式方法和重新参数化式方法三种主流的参数高效微调技术(PEFT)。微调模型可以让模型更适合于我们当前的下游任务,但当模型过大或数据集规模很大时,单个加速器&…...
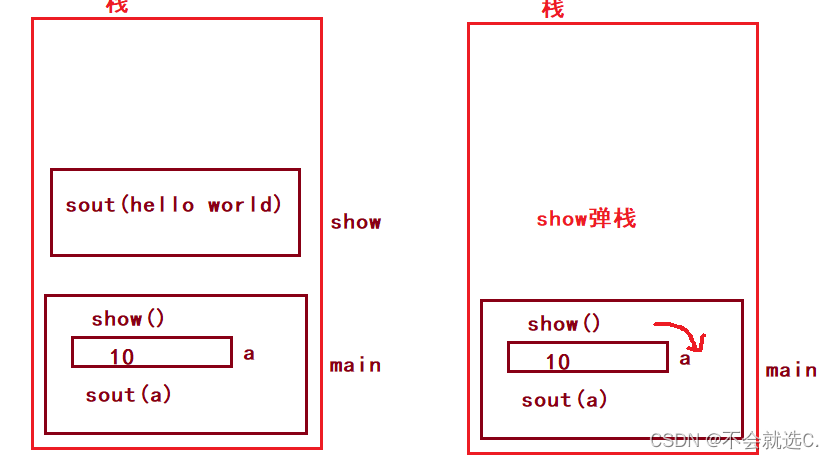
[正式学习java②]——数组的基本使用,java内存图与内存分配
一、数组的两种初始化方式 1.完整格式(静态初始化) 数据类型[] 数组名 new 数据类型[]{元素1,元素2…}; //范例 int[] arr new int[]{1,2,3,4}; 简化书写 一般我们会省略后面的 new 数据类型[] int[] arr {1,2,3,4}; 2.动态初始化 当不知道数组里面的初始值的时候…...

ESP32网络开发实例-TCP服务器数据传输
TCP服务器数据传输 文章目录 TCP服务器数据传输1、IP/TCP简单介绍2、软件准备3、硬件准备4、TCP服务器实现本文将详细介绍在Arduino开发环境中,实现一个ESP32 TCP服务器,从而达到与TCP客户端数据交换的目标。 1、IP/TCP简单介绍 Internet 协议(IP)是 Internet 的地址系统,…...

四川天蝶电子商务有限公司抖音电商服务引领行业标杆
随着电子商务的飞速发展,四川天蝶电子商务有限公司作为一家领先的抖音电商服务提供商,已经脱颖而出。本文将详细解析四川天蝶电子商务有限公司的抖音电商服务,让您一探究竟。 一、卓越的服务理念 四川天蝶电子商务有限公司始终坚持以客户为中…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...
