二叉树与递归的相爱相杀
数据结构之二叉树
- 一、基于二叉树的基础操作
- 1.二叉树的构建
- 2.二叉树的遍历
- ①前序遍历(深度遍历)
- ②中序遍历
- ③后序遍历
- ④层序遍历
- 判断一棵二叉树是否是完全二叉树(基于层序遍历的思想)
- 3.二叉树的数量问题
- ①求二叉树结点个数
- ②求二叉树叶子结点个数
- ③求二叉树第K层结点个数
- 4.查找某个结点所在位置
- 5.二叉树的高度
- 二、与二叉树相关的练习题(点击标题即可跳转至对应题目)
- 1.单值二叉树
- 2.判断两棵二叉树是否相同
- 3.对称二叉树
- 4.另一棵树的子树
- 4.二叉树的前序遍历
- 6.二叉树的构建及遍历
- 三、第一部分的全部代码(复制粘贴到vs一定能跑通)
- BinaryTree.h
- BinaryTree.c
- test.c
一、基于二叉树的基础操作
1.二叉树的构建
先看下面两句话
我们整个操作是建立在三个文件上的。BinaryTree.h放置全部需要引用的头文件、二叉树结点的定义以及所有自定义函数的声明;BinaryTree.c放置所有自定义函数的实现(这里并不是很准确,有一些自定义函数是供其他一些自定义函数使用的函数是可以不用放到.h文件中去的,.h文件中放置的自定义函数主要是在test.c文件中需要使用的函数)test.c就放置主函数,供我们测试二叉树写得是否正确。其中BinaryTree.c和test.c文件引用BinaryTree.h
前序遍历构建方法在第六道练习题中体现
刚开始我们用很简单的方法构建(三步搞定)
第一步:首先我们要定义单个结点
//BinaryTree.h
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;int val;
}BTNode;
第二步:基本架构
//test.c
int main()
{//构建6个节点BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);//建立这六个节点的指向关系node1->left = node2;node2->left = node3;node1->right = node4;node4->left = node5;node4->right = node6;
}
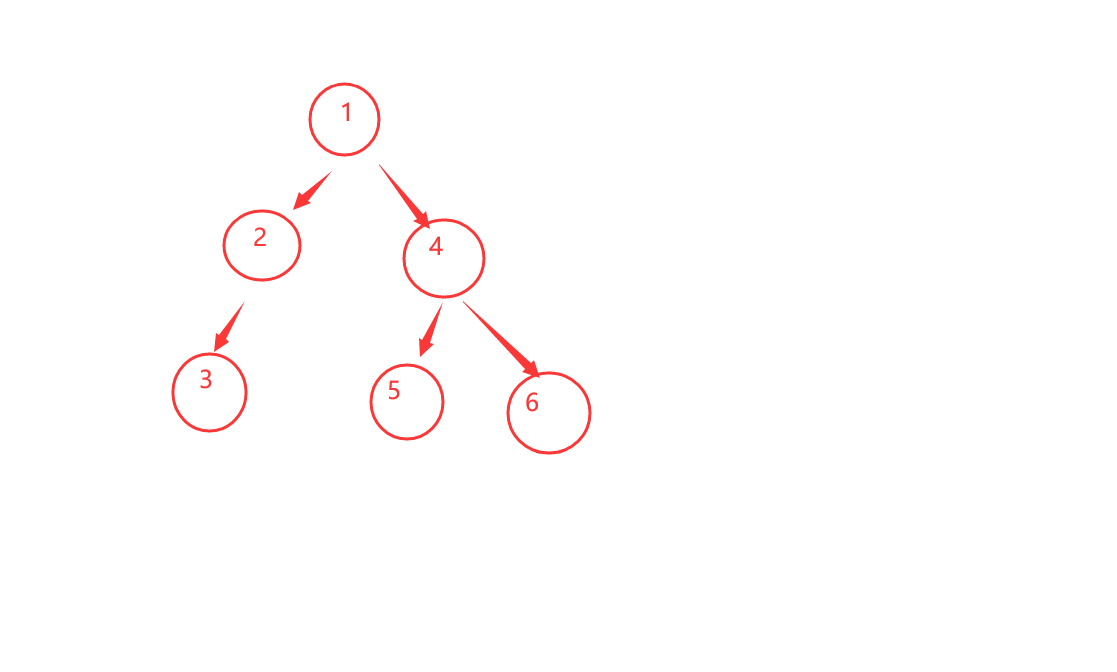
第三步:把BuyNode函数补上
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc failed");exit(-1);}node->left = NULL;node->right = NULL;node->val = x;return node;
}
2.二叉树的遍历
①前序遍历(深度遍历)
正如文章标题所说的,二叉树与递归相爱相杀,所以这里必然用的是递归来遍历
至于原因呢,就是二叉树是一个很好的递归结构(二路递归)
- 就拿前序遍历来说,先访问根,然后是左子树,右子树。其中访问左子树的时候,也是先访问左子树的根结点、左子树的左子树、左子树的右子树
- 这就很好的满足了递归的思想——把大问题化成与其类似的规模较小的子问题,通过递归调用解决小问题。
- 要注意的每次递归都会使问题变得更简单,直到问题已经简单到不需要进一步递归即可解决
- 递归的两个关键属性是基本情况和递推关系。基本情况是指递归过程中不再继续递归的条件,而递推关系则是将所有其他情况转换为基本情况的规则。
- 一般情况下基本情况写在递推关系前面
void PreOrder(BTNode* root)
{//前面说到的,这就是递归的基本情况----递归不再继续的条件if (root == NULL)return;//递归的基本关系----大问题化小问题printf("%d ", root->val);//先访问根,遇到根就打印PreOrder(root->left);//根访问完,访问左子树PreOrder(root->right);//再访问右子树
}递归图,按顺序走
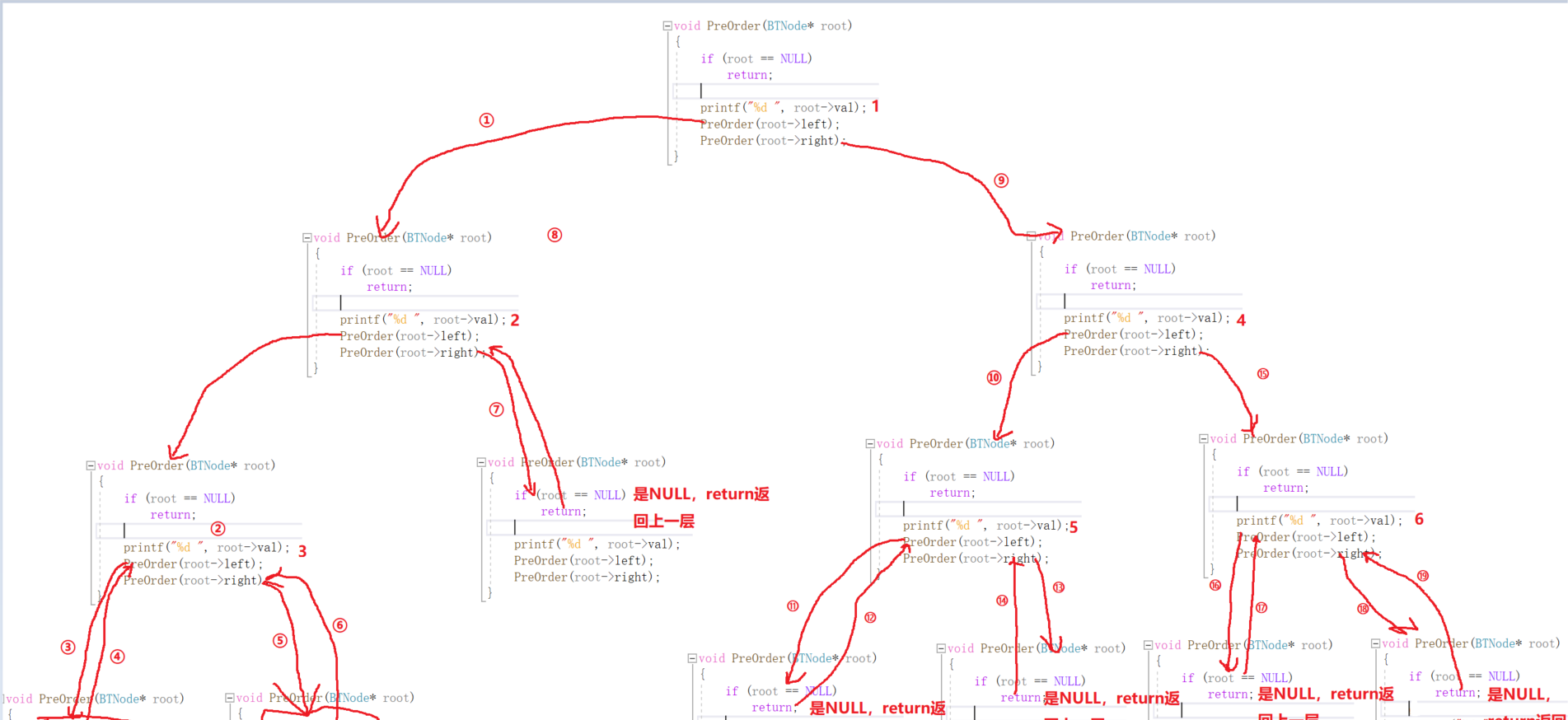
最终打印结果(空未打印)

②中序遍历
中序、后序和前序很类似,只是改一下根节点访问时机,这里我就放一下代码
void InOrder(BTNode* root)
{if (root == NULL)return;InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}
③后序遍历
void PastOrder(BTNode* root)
{if (root == NULL)return;PastOrder(root->left);PastOrder(root->right);printf("%d ", root->val);
}
④层序遍历
层序遍历要结合队列来解决
- 二叉树的层序遍历利用队列的原因主要在于队列的先进先出(FIFO)特性。
层序遍历的目标是按层级顺序遍历二叉树的所有节点。- 具体地说,首先将二叉树的根节点推入队列,然后检查队列是否为空。如果不为空,就从队列中取出队头的元素,并访问这个元素代表的节点。
然后,如果这个节点有左子树,就将左子树推入队列;如果有右子树,也将右子树推入队列。重复这个过程,直到队列为空。- 这样做的原因是,队列保证了我们总是先处理最先进入队列的节点,即按照层级顺序进行遍历。同时,这种方法适用于各种不同的二叉树结构
代码如下:(前提是有队列这个数据结构哈,没有的我会把代码一起放在第三部分,这里就展示层序遍历这部分的代码)
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);// 首先根不为空,让根进队列if (root != NULL)QueuePush(&q, root);//在队列不为空的情况下while (!QueueEmpty(&q)){//读取对头元素printf("%d", QueueFront(&q)->val);//在左右子树不为空的情况下,让左右子树入队列if (QueueFront(&q)->left != NULL)QueuePush(&q,QueueFront(&q)->left);if (QueueFront(&q)->right != NULL)QueuePush(&q, QueueFront(&q)->right);//让对头元素出队列QueuePop(&q);}QueueDestroy(&q);
}
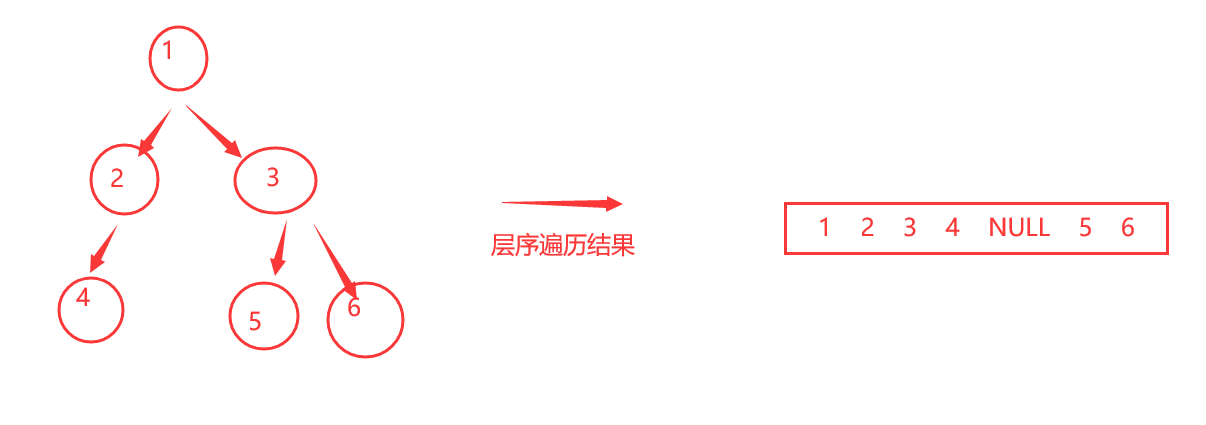
层序遍历的过程如下图(子树为空的时候不进队列)
判断一棵二叉树是否是完全二叉树(基于层序遍历的思想)
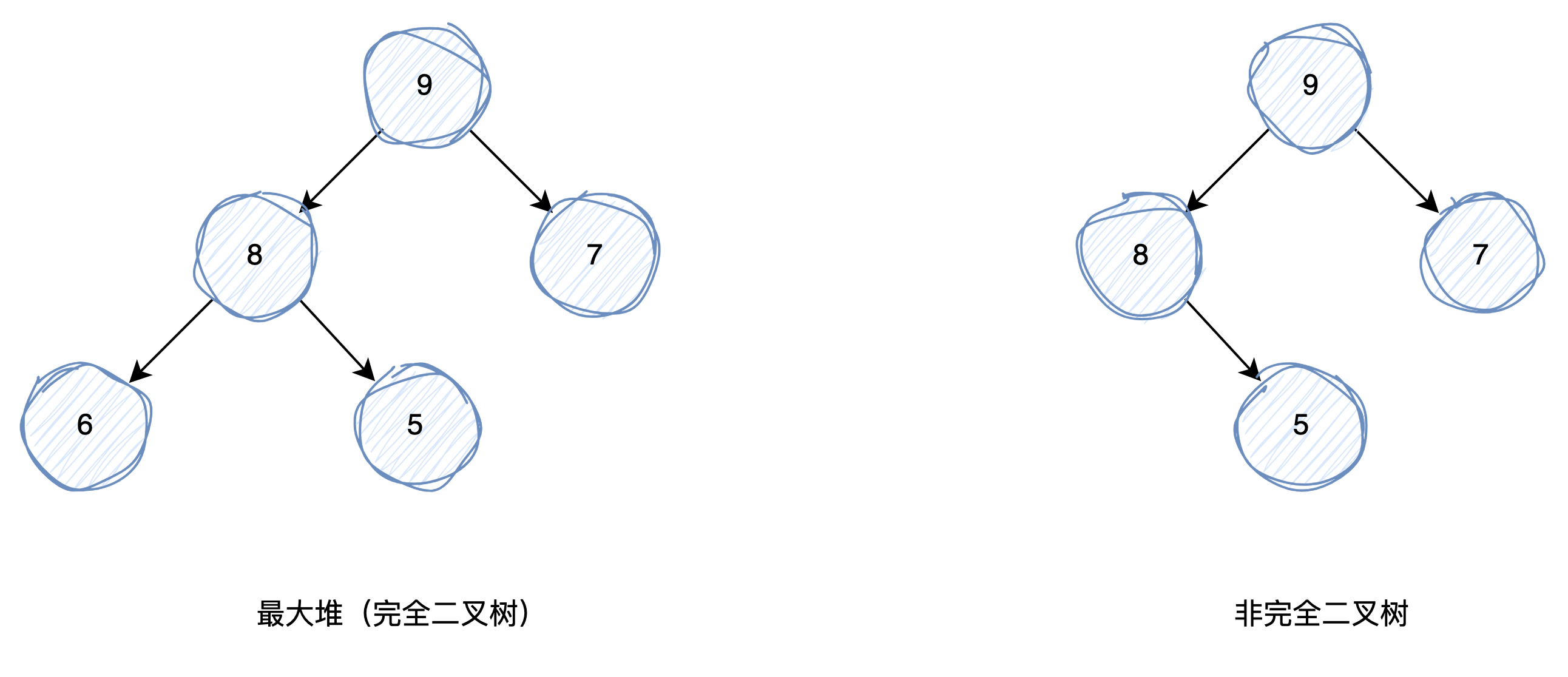
- 完全二叉树的特点大家还记得吗,就是假如完成二叉树有k层,那么其前k-1层都是满的,而第k层所有结点都连续集中在最左边
- 那么如何和层序遍历结合起来呢,就是我们按照层序遍历的方式一次将每一层入队列,然后出结点,接着带入左右子树。左右子树为空的时候也要入进去,就入个空值就好
- 如果不是完全二叉树,那么在出队列时遇到空值时,队列里还有非空元素。而如果是完全二叉树,遇到空值的时候也代表则元素已经遍历完了
非完全二叉树
完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root == NULL)return 1;QueuePush(&q, root);while (!QueueEmpty(&q)){//此处碰到空值就跳出循环开始判断是否是完全二叉树if (QueueFront(&q) == NULL)break;//if (QueueFront(&q)->left != NULL)QueuePush(&q, QueueFront(&q)->left);//if (QueueFront(&q)->right != NULL)QueuePush(&q, QueueFront(&q)->right);QueuePop(&q);}//上述代码就是入队列的过程//走到这意味着遇到空,如果此时队列里都是空,则表示是完成二叉树while (!QueueEmpty(&q)){if (QueueFront(&q) == NULL){QueuePop(&q);continue;}//走到这里说明此时队列不为空,而出现了空值QueueDestroy(&q);return 0;}QueueDestroy(&q);return 1;
}
3.二叉树的数量问题
①求二叉树结点个数
递归思想:要求二叉树结点的个数,可以化为求左子树的结点个数+右子树结点个数+1(这个1就是算上根结点)
//相当于二叉树的后序遍历
int TreeSize(BTNode* root)
{//写法1//if (root == NULL)// return 0;划分为左树的节点数+右树的节点数+1//return TreeSize(root->left) + TreeSize(root->right) + 1;//写法2//更简洁的写法return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
②求二叉树叶子结点个数
思路和上一题类似,只不过是找到叶子结点才算数
int TreeLeafSize(BTNode* root)
{//1.空节点返回0if (root == NULL)return 0;//注意,这里不能写成 return ; 因为 return ; 时默认就return 1回去,所以这样子求得的数值就是最后一层满载的时候的节点个数//2.叶子节点返回1if (root->left == NULL && root->right == NULL)return 1;//3.其他节点就递归到左右子树return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}③求二叉树第K层结点个数
- 这个有难度了,该怎么求第k层的结点个数呢?
- 其实也是递归的思想:求从根结点开始的第k层的个数,等同于求从第二层开始的第k-1层的结点个数,也等同于求从第三层开始的第k-2层结点的个数。。。。。。
int TreeKLevelSize(BTNode* root, int k)
{if (root == NULL)return 0;//从第一层看第k层等于第二层看第k-1层//走到这k == 1时表示递归走到了该层,此时节点不会为空,,即表示这层有节点if (k == 1)return 1;//二叉树中双路递归的思想真的很重要!!!return TreeKLevelSize(root->left, k - 1) + TreeKLevelSize(root->right, k - 1);
}
4.查找某个结点所在位置
- 看到这个问题,大概思路大家肯定都能想到,就遍历呗,在遍历的过程中比较值是否相等呗,很简单
- 但是这里有个问题哈,我们函数的返回值是找到的结点的地址,如果直接return回去,假如我们最开始就找到了这个地址,但是在后续的递归过没找到。而这个地址被NULL值覆盖了怎么办?
-解决办法就是:加个判断,当ret不等于NULL时才return,这样子及时在函数最开始root == NULL时(即到了叶子结点)返回了NULL,但在后续对ret的判断时也不会让NULL覆盖真正的地址
BTNode* BinaryTreeFind(BTNode* root, int x)
{if (root == NULL)return NULL;else if (root->val == x)return root;BTNode* ret = NULL;//通过判空的方式很好的解决了如果后续的值不符合时返回的null值如何规避ret = BinaryTreeFind(root->left,x);if (ret != NULL)return ret;ret = BinaryTreeFind(root->right,x);if (ret != NULL)return ret;
}5.二叉树的高度
- 有了上面这些递归事例的基础,看这个问题就很简单了
- 思路就是二叉树的高度等于左右子树的中较高的高度+1,然后再把子树给向下递归即可
int BinaryTreeHeight(BTNode* root)
{if (root == NULL)return 0;int LeftHeight = BinaryTreeHeight(root->left);int RightHeight = BinaryTreeHeight(root->right);return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}
- 不过这里要注意一个问题
- 很多同学为了偷懒而像下面这样简写是不对的
- 这样子看似代码简洁,但是这个代码的效率很低,你看不论较高的子树是左子树还是右子树,比较完之后还需要计算一遍左右子树的高度,效率很低!
int BinaryTreeHeight(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeHeight(root->left) > BinaryTreeHeight(root->right) ? BinaryTreeHeight(root->left) + 1 : BinaryTreeHeight(root->right)+ 1;
}
二、与二叉树相关的练习题(点击标题即可跳转至对应题目)
1.单值二叉树
- 思路:判断二叉树是不是单值二叉树,就是看其左右子树是不是单值二叉树
- 在这个递归的题目中,有一点很重要的就是,既然是判断是否,那肯定就是有些条件下是return false,有些条件是return true,所以代码中第二个if处不能写成
if(root->left = = NULL && root->left->val == root->val)
return true;
这个条件其实是继续递归的条件,你在这里就return了,如果后面还有不等的情况怎么办?
bool isUnivalTree(struct TreeNode* root){if(root == NULL)return true;if(root->left != NULL && root->left->val != root->val)return false;if(root->right != NULL && root->right->val != root->val)return false;return isUnivalTree(root->left) && isUnivalTree(root->right);
}
2.判断两棵二叉树是否相同
这个题相对来说就比较简单了,但是这个题是下个题的基础
bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL && q == NULL)return true;//走到这里肯定只有一个会为空,一空一非空肯定不相等if(p == NULL || q == NULL)return false;//走到这里肯定两个都不为空if(p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
3.对称二叉树
把上一题的两棵树合成一棵树了
bool isSame(struct TreeNode* p,struct TreeNode* q)
{if(p == NULL && q == NULL)return true;if(p == NULL || q == NULL)return false;if(p->val != q->val)return false;return isSame(p->left,q->right) && isSame(p->right,q->left);
}bool isSymmetric(struct TreeNode* root){return isSame(root->left,root->right);
}
4.另一棵树的子树
思路:让root及其子树依次的去和subRoot比较,用于比较的函数就是上上一题所写的
bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL && q == NULL)return true;//走到这里肯定只有一个会为空if(p == NULL || q == NULL)return false;//走到这里肯定两个都不为空if(p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}//subRoot不动root动bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root == NULL)return false;if(root->val == subRoot->val){//为什么不直接return isSameTree,因为这里如果isSameTree结果是false,并不能直接return回去,因为还要去子树继续比较,唯一返回false的条件就是走到空了if(isSameTree(root,subRoot))return true;}//这里用‘或’就行,只要子树有一个满足条件就OK了return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}
4.二叉树的前序遍历
这里题目要求,需要把遍历的结果放入数组中,所以我们需要先计算树中有多少个结点,然后构建多大的数组。
int TreeSize(struct TreeNode* root)
{if (root == NULL)return 0;return TreeSize(root->left) + TreeSize(root->right) + 1;
}// static int i = 0;
void PreTree(struct TreeNode* root, int* a,int* pi)
{if (root == NULL)return;a[(*pi)++] = root->val;//如果直接定义普通的i,那么在两路递归里这俩i是形参,值改变了对另外一个i没有影响PreTree(root->left, a,pi);PreTree(root->right,a, pi);
}//returnSize是返回数组的元素个数,要返回的还是数组!!!
int* preorderTraversal(struct TreeNode* root, int* returnSize) {int n = TreeSize(root);int* a = (int*)malloc(sizeof(int) * n);int i = 0;PreTree(root, a,&i);*returnSize = n;return a;
}
这俩就留着你们来砍瓜切菜了
二叉树的中序遍历
二叉树的后序遍历
6.二叉树的构建及遍历
- 实现是构建,思路也是用递归,这里我用前序遍历构建,既然是前序遍历,那我们是按照根-左-右的顺序来的,所以先构建根结点,然后递归调用CreateTree,最后别忘了终止条件——在遇到’#'代表着空节点,记得return NULL
-遍历的话,就按照题目要求的后序遍历即可
#include <stdio.h>
#include<stdlib.h>typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;char val;
}BTNode;BTNode* CreateTree(char* str,int* pi)
{if(str[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->val = str[*pi];(*pi)++;root->left = CreateTree(str,pi);root->right = CreateTree(str,pi);return root;
}void InOrder(BTNode* root)
{if(root == NULL){return;}InOrder(root->left);printf("%c ",root->val);InOrder(root->right);
}int main() {char str[100];scanf("%s",str);int i = 0;BTNode* root = CreateTree(str,&i);InOrder(root);return 0;
}
三、第一部分的全部代码(复制粘贴到vs一定能跑通)
BinaryTree.h
#pragma once#include<stdio.h>
#include<stdlib.h>typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;int val;
}BTNode;BTNode* BuyNode(int x);void PreOrder(BTNode* root);
void InOrder(BTNode* root);
void PastOrder(BTNode* root);int TreeSize(BTNode* root);
int TreeLeafSize(BTNode* root);
int TreeKLevelSize(BTNode* root, int k);void LevelOrder(BTNode* root);//层序遍历BTNode* BinaryTreeFind(BTNode* root, int x);
void BinaryTreeDestroy(BTNode* root);
//是完全二叉树返回1,否则返回0
int BinaryTreeComplete(BTNode* root);
int BinaryTreeHeight(BTNode* root);
BinaryTree.c
#define _CRT_SECURE_NO_WARNINGS 1#include"BinaryTree.h"
#include"Queue.h"BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc failed");exit(-1);}node->left = NULL;node->right = NULL;node->val = x;return node;
}void PreOrder(BTNode* root)
{if (root == NULL)return;printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL)return;InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}void PastOrder(BTNode* root)
{if (root == NULL)return;PastOrder(root->left);PastOrder(root->right);printf("%d ", root->val);
}//相当于二叉树的后序遍历
int TreeSize(BTNode* root)
{//if (root == NULL)// return 0;划分为左树的节点数+右树的节点数+1//return TreeSize(root->left) + TreeSize(root->right) + 1;//更简洁的写法(不过有弊端,在下个函数提)return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}//这个写法ok
//int TreeLeafSize(BTNode* root)
//{
// //这里也要记得判断
// //当递归不断深入时,遇到NULL不能继续使用了
// if (root == NULL)
// return;
//
// static count = 0;
//
// if (root->left == NULL && root->right == NULL)
// count++;
//
// TreeLeafSize(root->left);
// TreeLeafSize(root->right);
//
// return count;
// //这里在递归里可以return是因为虽然随着递归的进行,每次递归分路回流的时候都会return一次count
// //但是最后正确的count会覆盖之前的值
//}//递归写法
int TreeLeafSize(BTNode* root)
{//1.空节点返回0if (root == NULL)return 0;//为什么这里空节点 return; 时结果却是4呢//经测试,return ; 时默认就return 1回去,所以这样子求得的数值就是最后一层满载的时候的节点个数//2.叶子节点返回1if (root->left == NULL && root->right == NULL)return 1;//3.其他节点就递归到左右子树return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}int TreeKLevelSize(BTNode* root, int k)
{if (root == NULL)return 0;//从第一层看第k层等于第二层看第k-1层//k == 1时表示递归走到了该层,此时节点不会为空,,即表示这层有节点if (k == 1)return 1;//二叉树中双路递归的思想真的很重要!!!return TreeKLevelSize(root->left, k - 1) + TreeKLevelSize(root->right, k - 1);
}BTNode* BinaryTreeFind(BTNode* root, int x)
{if (root == NULL)return NULL;else if (root->val == x)return root;BTNode* ret = NULL;//通过判空的方式很好的解决了如果后续的值不符合时返回的null值如何规避ret = BinaryTreeFind(root->left,x);if (ret != NULL)return ret;ret = BinaryTreeFind(root->right,x);if (ret != NULL)return ret;
}//后序遍历销毁
void BinaryTreeDestroy(BTNode* root)
{if (root == NULL)return;BinaryTreeDestroy(root->left);BinaryTreeDestroy(root->right);free(root);//在这里置空无用,因为是形参//root = NULL;
}//要利用队列先进先出的特点
//最高层先入队列,然后依次出队列,在出队列的过程中将左右子树带入队列,直到队列为空
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root != NULL)QueuePush(&q, root);while (!QueueEmpty(&q)){printf("%d", QueueFront(&q)->val);if (QueueFront(&q)->left != NULL)QueuePush(&q,QueueFront(&q)->left);if (QueueFront(&q)->right != NULL)QueuePush(&q, QueueFront(&q)->right);QueuePop(&q);}QueueDestroy(&q);
}//思路类似层序遍历,只不过在入队列的时候要把左右子树全部入进去,即时是为空的情况下
//为什么呢,因为完全二叉树在物理结构上一定是连续的
//如果队列还没出完的情况下,就已经遇到空值了,说明就不是完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root == NULL)return 1;QueuePush(&q, root);while (!QueueEmpty(&q)){if (QueueFront(&q) == NULL)break;//if (QueueFront(&q)->left != NULL)QueuePush(&q, QueueFront(&q)->left);//if (QueueFront(&q)->right != NULL)QueuePush(&q, QueueFront(&q)->right);QueuePop(&q);}//走到这意味着遇到空,如果此时队列里都是空,则表示是完成二叉树while (!QueueEmpty(&q)){if (QueueFront(&q) == NULL){QueuePop(&q);continue;}QueueDestroy(&q);return 0;}QueueDestroy(&q);return 1;
}int BinaryTreeHeight(BTNode* root)
{if (root == NULL)return 0;int LeftHeight = BinaryTreeHeight(root->left);int RightHeight = BinaryTreeHeight(root->right);return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}
test.c
#define _CRT_SECURE_NO_WARNINGS 1#include"BinaryTree.h"
#include"Queue.h"int main()
{//手动构建一棵树BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);//BTNode* node7 = BuyNode(7);//BTNode* node8 = BuyNode(8);node1->left = node2;node2->left = node3;//node2->right = node7;node1->right = node4;node4->left = node5;node4->right = node6;//node3->right = node8;//前中后序// //PreOrder(node1);//printf("\n");////InOrder(node1);//printf("\n");//PastOrder(node1);//printf("\n");//总节点数、叶子节点数、第k层节点数// //printf("%d\n", TreeSize(node1));//printf("%d\n", TreeLeafSize(node1));//count = 0;//这里有个缺陷就是使用static局部变量之后这个函数只能调用一次//printf("%d\n", TreeLeafSize(node1));//printf("%d", TreeKLevelSize(node1,3));//BTNode* ret = BinaryTreeFind(node1,5);//printf("%d", ret->val);//BinaryTreeDestroy(node1);//node1 = NULL;//在外面置空一下就好了//LevelOrder(node1);//printf("%d", BinaryTreeComplete(node1));//printf("%d", BinaryTreeHeight(node1));return 0;
}
相关文章:

二叉树与递归的相爱相杀
数据结构之二叉树 一、基于二叉树的基础操作1.二叉树的构建2.二叉树的遍历①前序遍历(深度遍历)②中序遍历③后序遍历④层序遍历判断一棵二叉树是否是完全二叉树(基于层序遍历的思想) 3.二叉树的数量问题①求二叉树结点个数②求二…...

Docker 安装 reids
docker run -itd --name myredis -p 6379:6379 redis --requirepass “123456” --restartalways --appendonly yes...

opensl学习——base16编码解码、base64编码解码、ASCII码表、扩展ASCII码
文章目录 ASCII表概述base家族简单说明 Hex(十六进制)编码、Base32编码、Base64编码、base256编码base16编码与解码base64编码概述转换过程不足 3 字节处理方法例子一,不足3字节,只有一个字节例子二,不足3字节,只有两个字节 base64示例代码1代码分析 acl…...

gazebo各种插件
类别 libgazebo_ros_api_plugin.so:提供与Gazebo仿真环境进行通信的API接口。 libgazebo_ros_block_laser.so:模拟激光传感器的插件。 libgazebo_ros_bumper.so:模拟碰撞传感器的插件。 libgazebo_ros_camera.so:模拟相机传感器的…...

C语言Free空指针会怎样?
在C语言中,使用free函数释放一个空指针是安全的,不会引发任何错误或异常。具体来说,当使用free函数释放一个空指针时,free函数会忽略这个空指针,并且不会执行任何操作。这是因为free函数只对有效的指针进行内存释放操作…...

软件测试全套教程,软件测试自学线路图
软件测试: 软件测试是为了发现程序中的错误而执行程序的过程。 通俗的说,软件测试需要在发布软件之前,尽可能的找软件的错误,尽量避免在发布之后给用户带来不好的体验,并要满足用户使用的需求。 现在市面上这么多软…...

禁止浏览器缩放
禁止浏览器缩放 1. 页面中添加如下代码:2. css单位统一使用rem,如下: 两个条件即可实现: 1. 动态修改html属性fontsize的值; 2. css单位统一使用rem。 1. 页面中添加如下代码: // 定义基准字体 new functi…...

前端食堂技术周刊第 100 期:TS 5.3 Beta、ViteConf2023、Rspress 1.0、Fresh 1.5、Chrome 118
美味值:🌟🌟🌟🌟🌟 口味:乌龙金桂 食堂技术周刊仓库地址:https://github.com/Geekhyt/weekly 大家好,我是童欧巴。欢迎来到前端食堂技术周刊,我们先来看下…...

汇川IT7000系列HMI使用脚本实现画面跳转时自动切换手自动模式
汇川IT7070E工业HMI使用实例(1) 用脚本切换模式 我们在使用工业HMI做画面时,可能会有这样的需求,希望切换画面时,可以根据不同的画面,自动切换相应的模式,比如有些画面是进行手动操作的,有些画面是进行自动操作的,当我们需要手动时,希望进入画面自动切换为“手动模…...
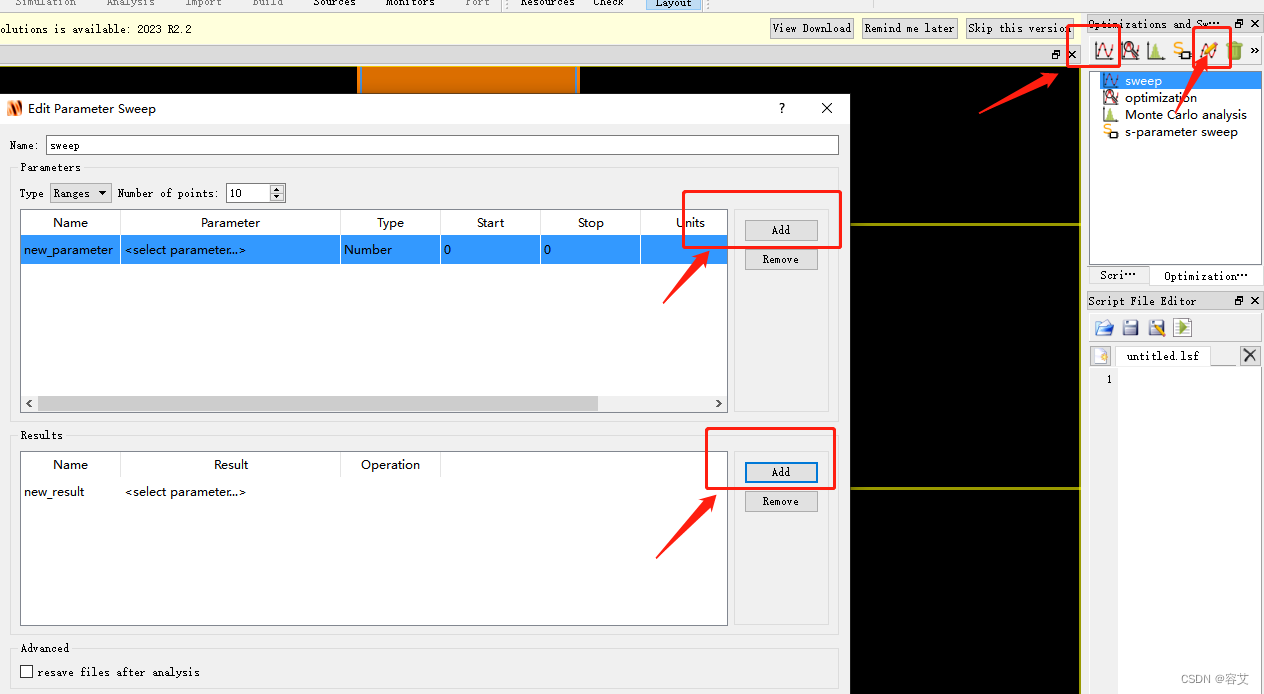
FDTD Solutions笔记
FDTD Solutions笔记 目录使用流程实例 目录 使用流程 实例 材料条件 步骤 基底 2. 添加规则膜层 3. 添加仿真区 解释: 仿真区为(0,0),x方向为0.4,y方向是1 解释: 一般先用低精度进行计算 解释:…...
 语法)
SQL SELECT DISTINCT(选择不同) 语法
SQL SELECT DISTINCT 语法 SELECT DISTINCT语法用于仅返回不同的(different)值。 在一张表内,一列通常包含许多重复的值; 有时你只想列出不同的(different)值。 SELECT DISTINCT语句用于仅返回不同的(diffe…...
常见的数据结构及应用
文章目录 前言数据结构介绍数组链表队列和栈树堆 总结 前言 数据结构是计算机存储、组织数据的方式。在工作中,我们通常会直接使用已经封装好的集合API,这样可以更高效地完成任务。但是作为一名程序员,掌握数据结构是非常重要的,…...
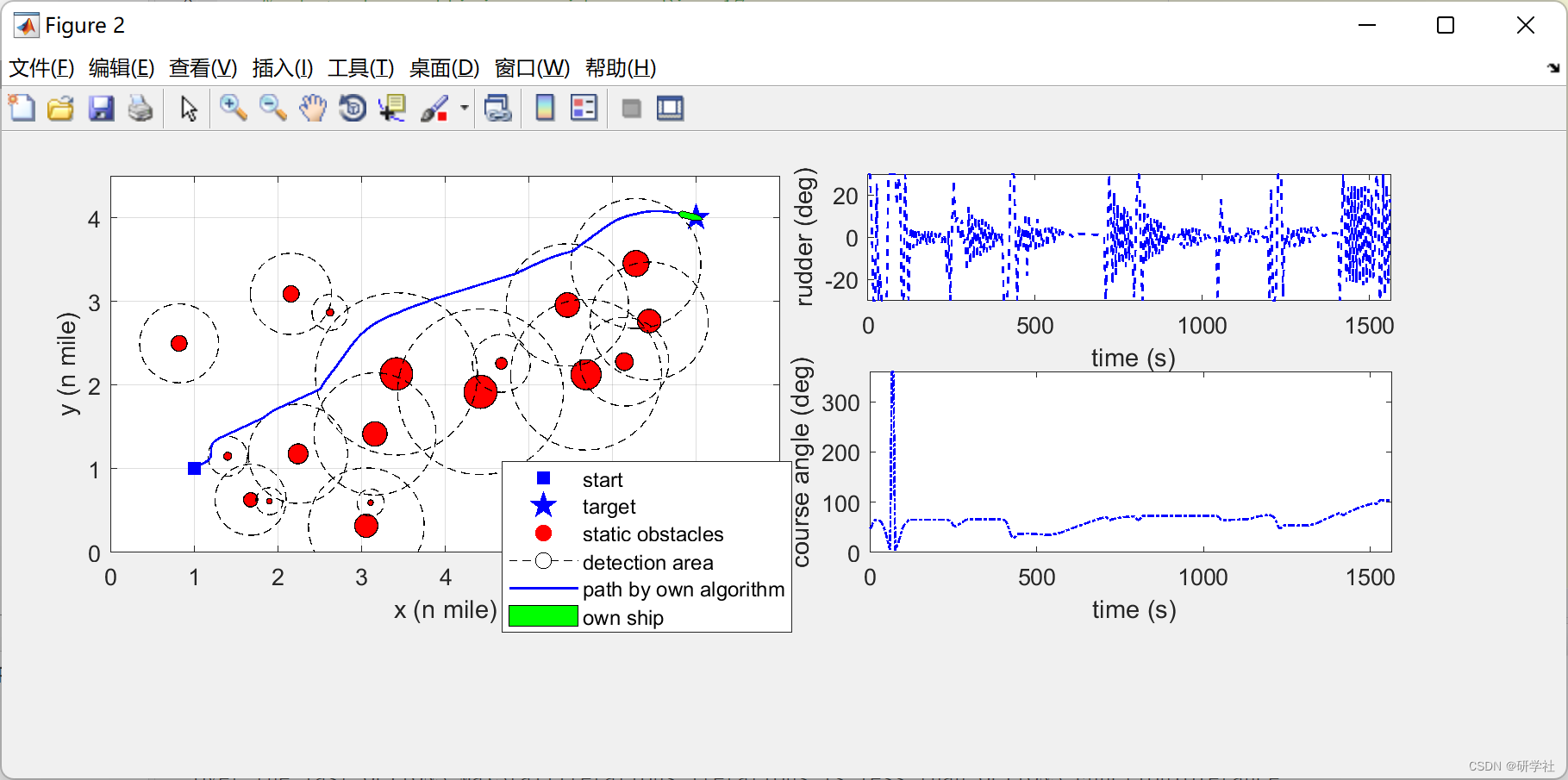
基于模型预测人工势场的船舶运动规划方法,考虑复杂遭遇场景下的COLREG(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
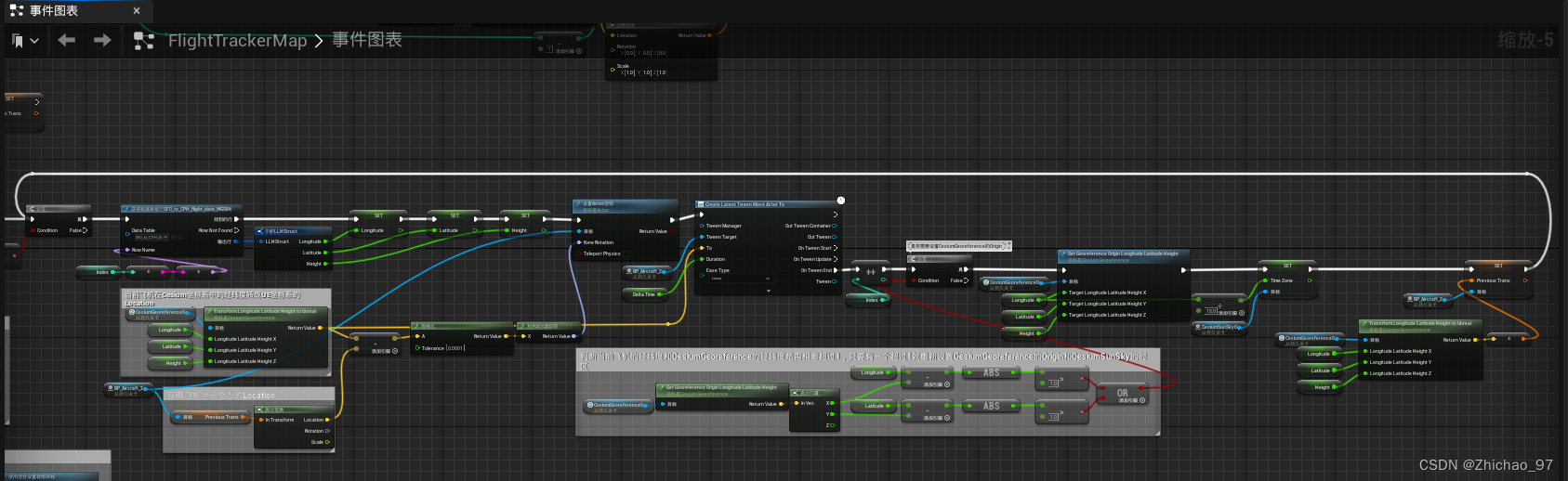
【UE5 Cesium】19-Cesium for Unreal 建立飞行跟踪器(4)
遗留问题 在上一篇博客中(【UE5 Cesium】18-Cesium for Unreal 建立飞行跟踪器(3)),我们实现了飞机变速飞行的功能,但是还存在两个问题,分别是: (1)由于UE的…...

TrustZone
TrustZone技术 让我们从最重要的问题开始:为什么存在TrustZone技术,它防御什么?保护用 C 和 C 编写的大型程序免受黑客攻击可能是一个挑战。内存损坏漏洞是一个常见问题,尽管消除它们是安全工程师的核心目标,但从操作…...

✔ ★【备战实习(面经+项目+算法)】 10.16学习时间表(总计学习时间:5h)
✔ ★【备战实习(面经项目算法)】 坚持完成每天必做如何找到好工作1. 科学的学习方法(专注!效率!记忆!心流!)2. 每天认真完成必做项,踏实学习技术 认真完成每天必做&…...

React + Router
React Router 这个只是专门讲解 React Router 新开的例子。 教程来源:https://reactrouter.com/en/main/start/tutorial 创建新项目 yarn create vite my-react-router-app --template react-ts cd my-react-router-app yarn安装 React Router 依赖: yarn add…...

微信小程序设置动态变量设值
微信小程序设置动态变量设值 微信小程序如何动态变量设值? 示例代码如下: setValFunc() {const key this.data.currentPickerid; // 业务需求动态键值key,或者是上一界面获取的动态key值const value 变量值;this.setData({[${key}]: valu…...

闪站侠洗衣洗鞋多门店多用户管理系统,洗鞋店干洗店小程序开发;
闪站侠洗护软件是多分店多用户管理系统,一个分店可以同时关联多个用户。闪站侠洗护管理软件通过互联网为洗衣店/洗鞋店干洗店提供加盟或直营连锁管理; 实现会员洗衣的门店收衣->上门收衣->开单拍照->清洗护理/工厂洗涤->微|信/短…...
JDBC增删改查示例
数据库表 CREATE TABLE customers ( id int NOT NULL AUTO_INCREMENT, name varchar(15) DEFAULT NULL, email varchar(20) DEFAULT NULL, birth date DEFAULT NULL, photo mediumblob, PRIMARY KEY (id) ) ENGINEInnoDB AUTO_INCREMENT39 DEFAULT CHARSETgb2312;…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...