【SPSS】单样本T检验分析详细操作教程(附案例实战)

🤵♂️ 个人主页:@艾派森的个人主页
✍🏻作者简介:Python学习者
🐋 希望大家多多支持,我们一起进步!😄
如果文章对你有帮助的话,
欢迎评论 💬点赞👍🏻 收藏 📂加关注+
目录
推断统计与参数检验
假设检验
单样本t检验
单样本t检验应用举例
推断统计与参数检验

推断统计
- 推断统计方法是根据样本数据推断总体特征的方法
- 推断统计包括参数估计 (点估计和区间估计)和假设检验两大类
参数检验 VS 非参数检验
- 参数检验(参数假设检验)
总体分布已知 (如总体为正态分布)的情况下,根据样本数据对总体分布的统计参数(如均值、方差等)进行推断
- 非参数检验(非参数假设检验)
总体分布未知的情况下,根据样本数据对总体的分布形式或数字特征进行推断
假设检验

假设检验的基本思想
1 首先,对总体参数值提出假设
2 然后,利用样本告知的信息去验证先前提出的假设是否成立
- 如果样本数据不能够充分证明和支持假设,则应拒绝假设
- 如果样本数据能够充分证明和支持假设,则不能推翻假设
小概率原理:
- 发生概率很小的随机事件在某一次特定的实验中是几乎不可能发生的
- 小概率原理是假设检验所依据的原理
假设检验的基本步骤
1.提出原假设(记为H0 )和备择假设(记为H1 ) 通常,将希望推翻的假设放在原假设上
2.选择检验统计量:检验统计量服从或近似服从某种已知的理论分布
3.计算概率P值:在认为原假设成立的条件下,根据样本数据和检验统计量计算 概率P值,该概率值间接地给出了样本值(或更极端值)在原假设成 立条件下发生的概率,即:P(拒绝H0|H0为真)
4.给定显著性水平α,并作出统计决策:显著性水平α是在原假设H0正确的前提下却拒绝原假设的概率,即“弃真”概率,一般设定为 0.05或0.01 若概率P值小于等于α,拒绝原假设;否则,不能拒绝原假设
单样本t检验

单样本t检验介绍
- 单样本t检验是指研究问题中仅涉及一个总体,且将采用t检验的方法进行分析
- 单样本t检验的前提是样本来自的总体应服从或近似服从正态分布
- 单样本t检验的目的:利用来自某总体的样本数据,推断该总体的均值是否与指定的检验值存在显 著差异,是对总体均值的假设检验
单样本t检验的基本步骤
1.提出原假设(记为H0 )和备择假设(记为H1 )
双侧检验:
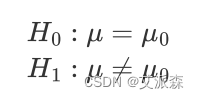
单侧检验:
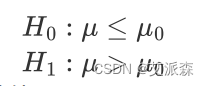
μ为总体均值;μ0为检验值
2.选择检验统计量
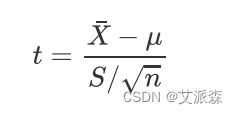
- S是样本标准差,n是样本容量
- t统计量的自由度为n-1
- 当认为原假设成立时,μ用μ0代入
3.计算概率P值
SPSS会自动将样本均值、μ0、样本标准差、样本容量代入 检验统计量,计算得到t统计量的观测值,同时依据t统计量所服从的分布计算其对应的概率P值
4.给定显著性水平α,并作出统计决策
若概率P值小于等于α,拒绝原假设;否则,不能拒绝原假设因为SPSS给出的是双侧概率P值,所以在单侧检验中,应将P/2与α进行比较
单样本t检验应用举例

【案例】 为研究信用卡消费现状,对某地区500名信用卡持有者进行了随机调查,得到其月平均刷卡金额数据。据估计,该地区信用卡月刷卡金额的平均值不低于3000元。现依据所获得的调查数据判断是否支持平均刷卡金额不低于3000元的假设。
分析:
由于该问题涉及的是单个总体,且进行总体均值检验,同时月刷卡金额的总体可近似认为服从正态分布,因此,可采用单样本t检验来进行分析。
操作步骤:
①选择菜单【分析】----> 【比较均值】----> 【单样本T检验】
②选择待检验的变量到【检验变量(T)】框中,在【检验值(V)】框中输入原假设中的检验值
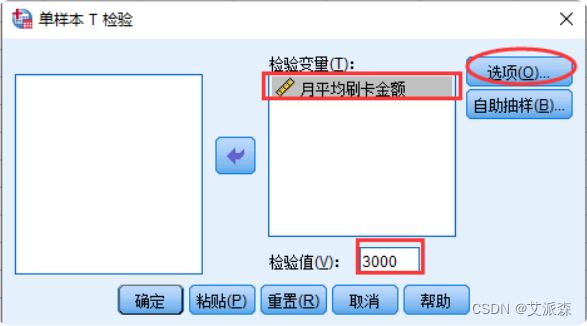
③点击【选项(O)】按钮指定缺失值的处理方法,并设置置信区间百分比
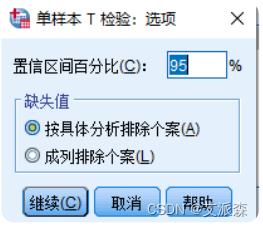
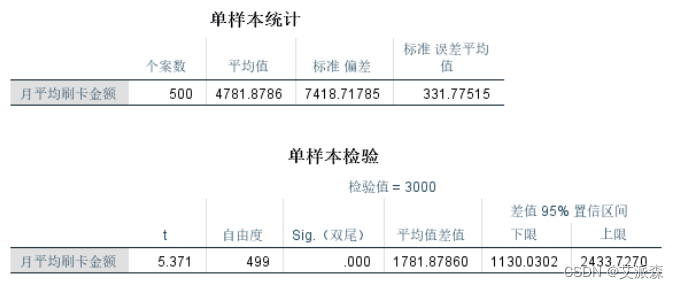
④分别点击“继续”、“确定”,分析结果如下:
结论:由以上分析可知:
从表一可得:500个被调查者月刷卡金额的平均值为4781.8786 元,标准差为7418.71785元,标准误差平均值(S/√n)为 331.77515;
从表二可得:t统计量的观测值为5.371,自由度为499(即n-1=500-1),Sig.(双尾)是t统计量观测值的双侧概率P值,平均值差值是样本均值与原假设检验值的差(4781.8786- 3000=1781.8786),这也是t统计量的分子部分,它除以表一的标 准误差平均值后得到t统计量的观测值,最后两列是总体均值μ与原 假设值μ0差的95%的置信区间,为(1130.0302,2433.7270),由此计算出总体均值的95%置信区间为(4130.0302,5433.7270)。 结合题意,可认为SPSS在分析的时候,原假设为:H0 :μ≤3000, 备择假设为: H1 :μ>3000,是一个单侧检验的问题,因此比较α和 p/2。由于p/2小于α,因此应该拒绝原假设,接受备择假设,认为该地区信用卡月刷卡金额的平均值与3000元有显著差异,且远远高 于3000元。另一方面,95%的置信区间也告诉我们有95%的把握认为月刷卡金额均值在4130.0~5433.7之间,3000元没有包含在置信区间内,也证实了上述推断。
相关文章:

【SPSS】单样本T检验分析详细操作教程(附案例实战)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
计算机网络笔记、面试八股(三)—— HTTPS协议
本章目录3. HTTPS协议3.1 HTTPS协议简介3.2 SSL/TLS协议3.2.1 SSL/TLS功能的实现3.3 HTTP和HTTPS的区别3.4 HTTPS协议的优点3.5 HTTPS协议的缺点3.6 HTTPS协议的工作流程3.7 HTTPS是如何解决HTTP的缺点的3.7.1 解决内容可能被窃听的问题——加密3.7.1.1 方法1.对称加密3.7.1.2 …...
浅谈liunx init.d 和 rc.local 两种起动方式
浅谈liunx init.d 和 rc.local 两种起动方式 以rabbitmq 举例 (一).init.d 方式 开机自动重启设置 1.在/etc/init.d 目录下新建一个 rabbitmq [rootlocalhost init.d]# vi rabbitmq具体脚本如下所示: #!/bin/bash # # chkconfig: 2345 …...

元宇宙+教育,正在引发哪些剧烈变革?机会在哪里?丨圆桌实录
图片来源:由无界AI绘画工具生成2月23日,温州元宇宙创新中心为2023年第一批申请入驻的项目企业举办了签约仪式。温州临境网络科技有限公司、温州好玩文化产业有限公司、温州云兮科技有限公司(筹)等企业完成签约。这意味着ÿ…...
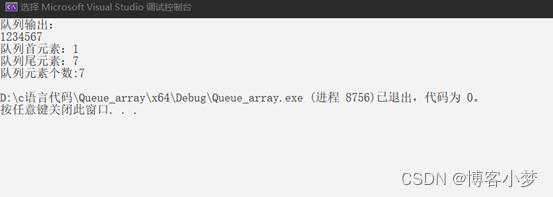
追梦之旅【数据结构篇】——详解C语言实现顺序队列
详解C语言实现顺序队列~😎前言🙌预备小知识🙌队列的概念及结构😊1.顺序队列头文件编写🙌2.Queue.c文件的编写🙌1)队列的初始化函数实现😊2)队列的销毁函数实现Ƕ…...

使用自己的数据集Fine-tune PaddleHub预训练模型
使用自己的数据Fine-tune PaddleHub预训练模型 果农需要根据水果的不同大小和质量进行产品的定价,所以每年收获的季节有大量的人工对水果分类的需求。基于人工智能模型的方案,收获的大堆水果会被机械放到传送带上,模型会根据摄像头拍到的图片…...

带组态物联网平台源码 代码开源可二次开发 web MQTT Modbus
物联网IOT平台开发辅助文档 技术栈:JAVA [ springmvc / spring / mybatis ] 、Mysql 、Html 、 Jquery 、css 使用协议和优势: TCP/IP、HTTP、MQTT 通讯协议 1.1系统简介 IOT通用物联网系统平台带组态,是一套面向通用型业务数据处理的系统…...

计算机网络的发展历程
计算机网络的历史可以追溯到20世纪60年代。那个时候,计算机还非常昂贵,只有少数大型机可以被用于处理重要任务。这些大型机通常被安装在大型企业、政府机构和大学中。由于这些机器非常昂贵,许多企业、机构和大学只能通过终端连接来访问它们。…...

【华为OD机试模拟题】用 C++ 实现 - 不含 101 的数(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

面试题-下单后位置信息上报的方案
面试题:外卖下单后每10min上报位置事件的具体实现方案。需要考虑哪些点。存储方案:考虑到数据量很大,需要快速响应查询请求,建议使用分布式存储方案,如 HBase、MongoDB 等。这些分布式存储系统可以水平扩展,…...
视觉人培训团队把它称之为,工业领域人类最伟大的软件创造,它的名字叫Halcon
目前为止,世界上综合能力强大的机器视觉软件,,它的名字叫Halcon。 视觉人培训团队把它称之为,工业领域人类最伟大的软件创造,它的名字叫Halcon。 持续不断更新最新的图像技术,软件综合能力持续提升。 综…...
干了2年的手工点点点,感觉每天浑浑噩噩,我的自动化测试之路...
作为一个测试人员,从业年期从事手工测试的工作是没有太多坏处的,当然,如果一直点来点去那么确实自身得不到提高,这时候选择学习自动化测试是一件很有必要的事情,一来将自己从繁重的重复工作中解放出来,从事…...
嵌入式系统硬件设计与实践(学习方法)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 刚读书的时候,对什么是嵌入式,其实并不太清楚。等到自己知道的时候,已经毕业很多年了。另外对于计算机毕业的学…...
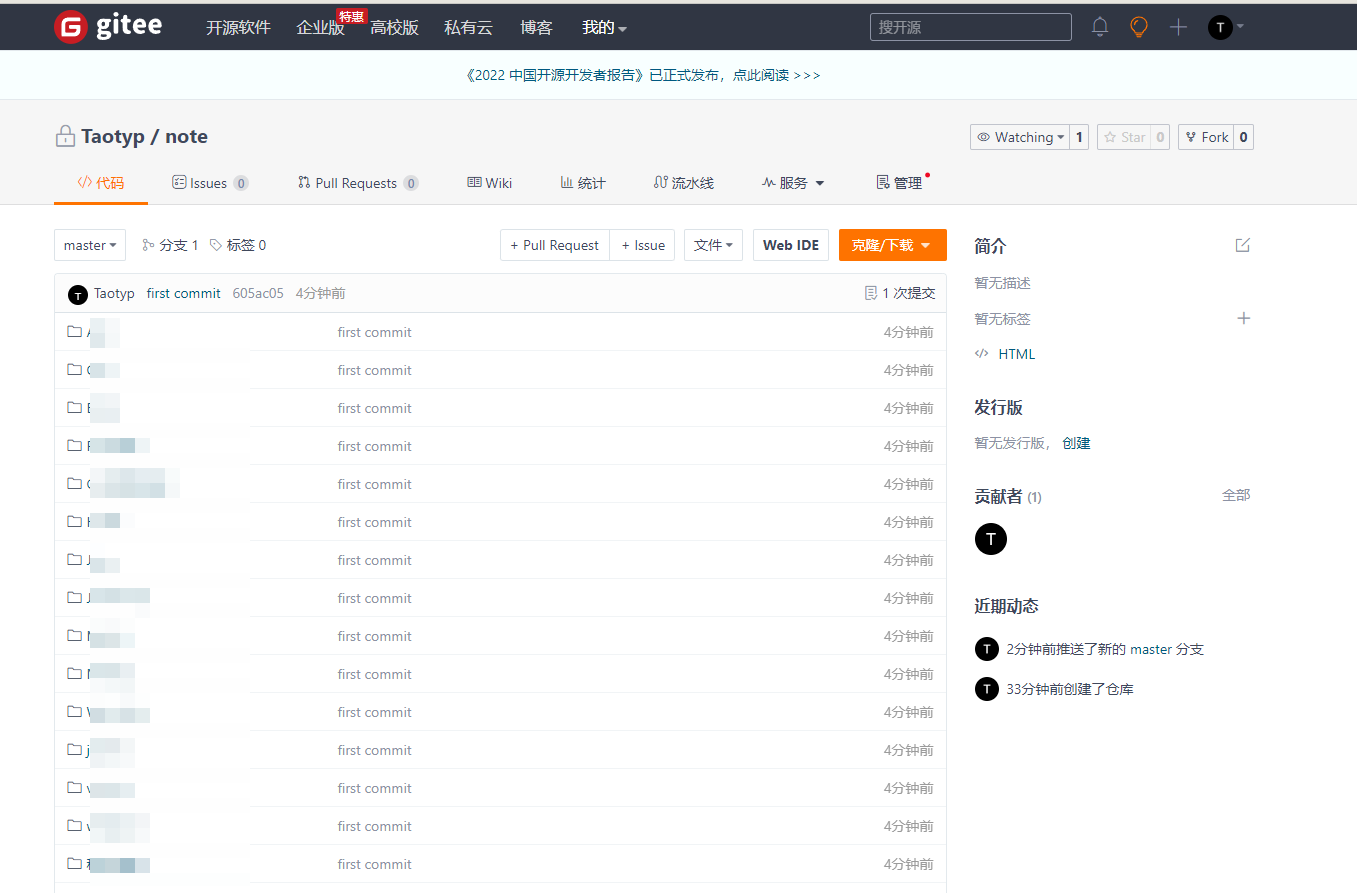
如何拥有自己的Gitee代码仓库
本教程适用码云代码托管平台 https://gitee.com/ 首先在电脑上安装Git(哔站有安装Git教程)和注册gitee账号后再来阅读此教程 1、在设置页面中点击 SSH公钥 2、点击 怎样生成公钥 3、点击公钥管理 4、点击 生成\添加SSH公钥 5、打开终端 输入如图红框中的…...
通用信息抽取技术UIE产业案例解析,Prompt 范式落地经验分享!
想了解用户的评价究竟是“真心夸赞”还是“阴阳怪气”?想快速从多角色多事件的繁杂信息中剥茧抽丝提取核心内容?想通过聚合相似事件准确地归纳出特征标签?……想了解UIE技术在产业中的实战落地经验?通用信息抽取技术 UIE 产业案例…...
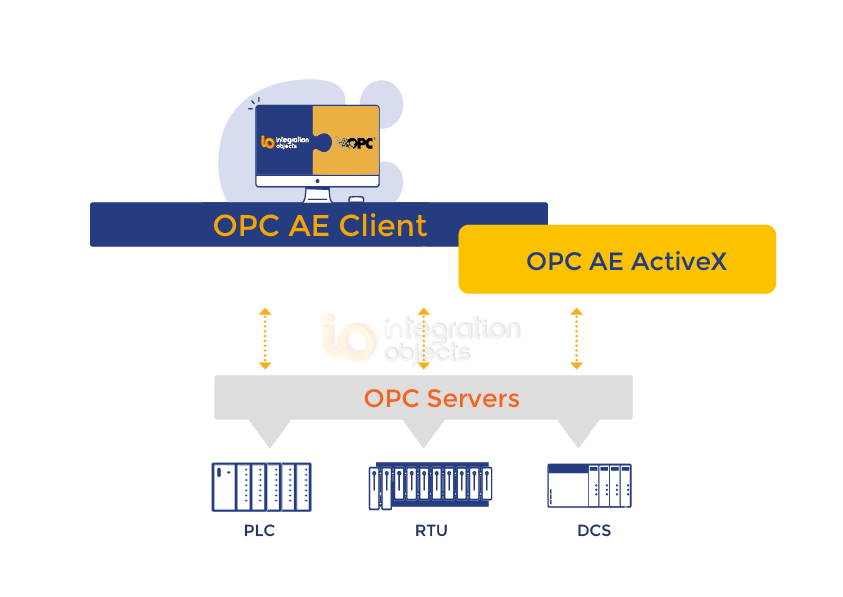
integrationobjects/OPC AE Client ActiveX Crack
使用 OPC AE 客户端 ActiveX 进行快速 OPC 警报和事件客户端编程! OPC AE Client ActiveX包括多个 OPC ActiveX 控件,可以轻松嵌入到最流行的 OLE 容器中。这允许用户与任何 OPC AE 服务器连接并实时检索警报和事件。 这种易于使用的 OPC AE ActiveX 简化…...
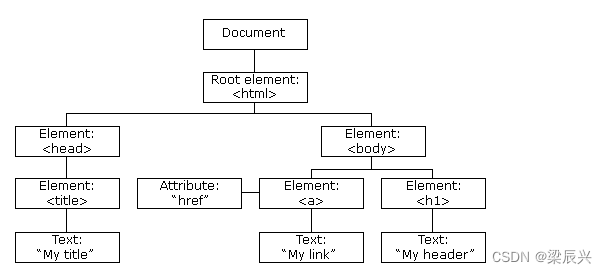
JavaScript HTML DOM 简介
文章目录JavaScript HTML DOM 简介HTML DOM (文档对象模型)HTML DOM 树查找 HTML 元素通过 id 查找 HTML 元素通过标签名查找 HTML 元素通过类名找到 HTML 元素下面我们将学到如下内容JavaScript HTML DOM 简介 通过 HTML DOM,可访问 JavaScript HTML 文档的所有元素…...
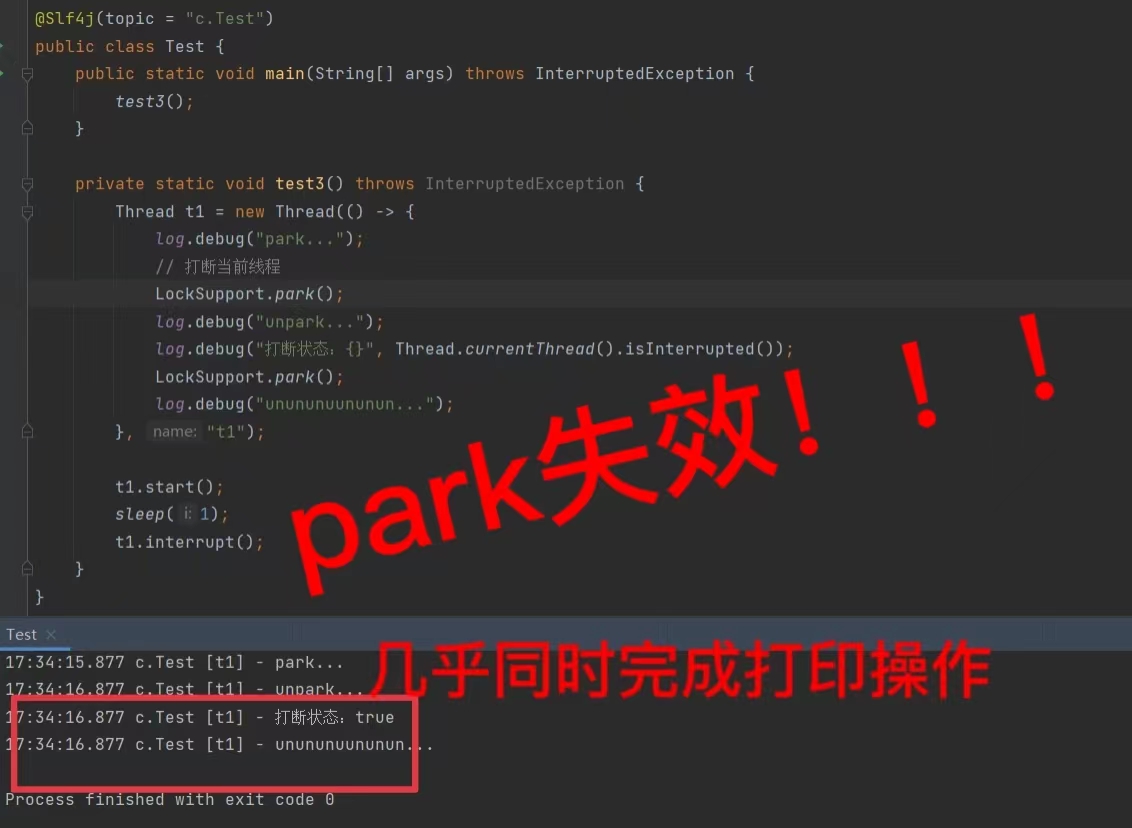
interrupt多线程设计模式
1. 两阶段终止-interrupt Two Phase Termination 在一个线程T1中如何“优雅”终止线程T2?这里的【优雅】指的是给T2一个料理后事的机会。 错误思路 ● 使用线程对象的stop()方法停止线程(强制杀死) —— stop()方法…...
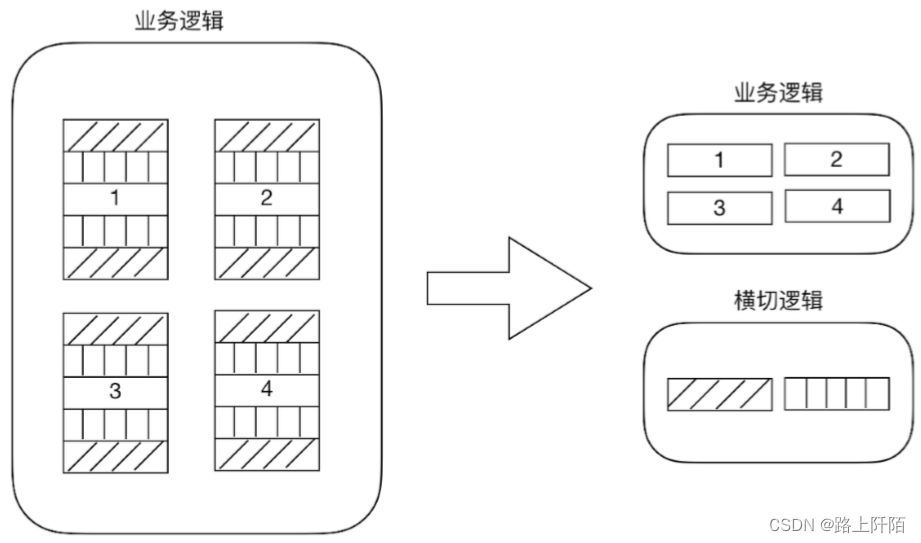
Spring IoC 和 Spring AOP
Spring IoC Ioc(Inversion of control:即控制反转)是一种设计思想,而不是一种具体的技术实现。IoC的思想就是将原本在程序中手动创建对象的控制权交给Spring框架来管理。 不过, IoC 并非 Spring 特有,在其…...

taobao.top.oaid.merge( OAID订单合并 )
¥开放平台免费API必须用户授权 基于OAID(收件人ID, Open Addressee ID)做订单合并,确保相同收件人信息的订单合并到相同组。 公共参数 请求地址: HTTP地址 http://gw.api.taobao.com/router/rest 公共请求参数: 公共响应参数: 请…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
