力扣环形链表(1)进阶环形链表(2)及环形链表的约瑟夫问题
为了加深对环形链表的理解和掌握,这两道题是很不错的选择。
这里所说环形链表不是一个圈圈的结构,而是带环链表。链接:环形链表(1)
注意这里链表的长度
所以要注意链表是否为空
第一种方法,应该是比较容易想到的方法(偷鸡取脚)
遍历链表,将每个节点的val更改为一个不容易想到的值,如666666,当遇到一个666666时就返回true,如果在遍历过程中一直走到空都再没有遇到一个666666,那就返回false。
代码如下bool hasCycle(struct ListNode *head) {struct ListNode*p=head;while(p){if(p->val!=666666){p->val=666666;p=p->next;}else return true;}return false; }这种方法明显是投机取巧,所以还有可能被抓到。
运行后还是也可以通过
双指针法(正经方法)
就想操场的跑道上,有跑的快的人和跑得慢的人,快的人会不断追上慢的人。
设置双指针,从head开始走,快指针一次跑两步,慢指针一次跑一步,链表中是有环的,快指针一定会抓到慢指针。
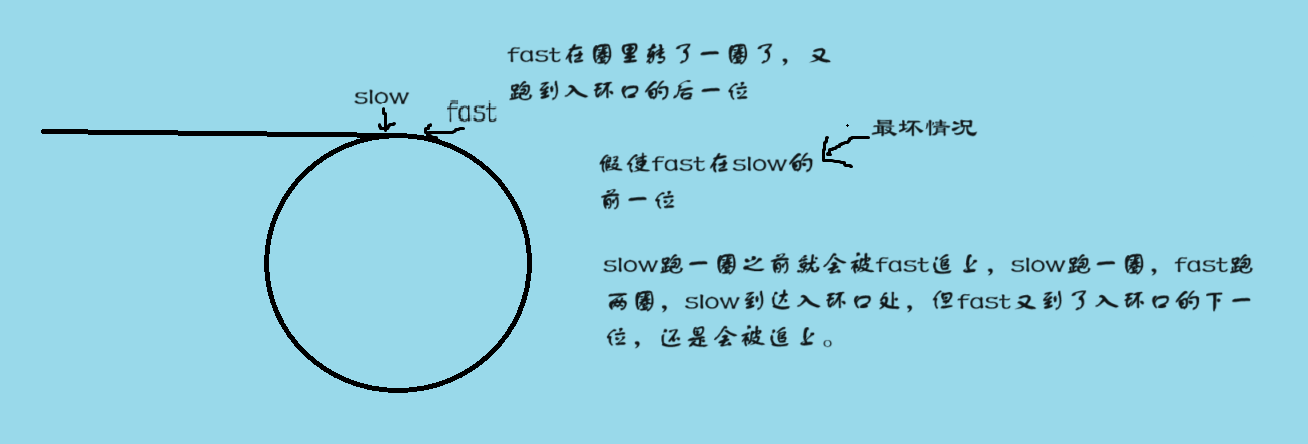
在慢指针进环时,快指针已经在环状里转圈圈了,慢指针一次走一步,快指针一次走两步,慢指针走半圈,快指针就走一圈。
代码如下bool hasCycle(struct ListNode *head) {struct ListNode*slow=head,*fast=head;while(fast&&fast->next){fast=fast->next->next;slow=slow->next;if(slow==fast){return true;}}return false; }一直找找找,如果有环一定会相遇。
思考:如果快指针一次走3步,还可以保证能抓到慢指针吗?
假使慢指针进环时,快慢指针差距m个位置,每次快指针与慢指针的距离差距减小为2,有两种情况。
- m为偶数
每次距离都减小2
m-2
m-4
m-6
…
4
2
0
最终快指针会遇到慢指针。
2. m为奇数
m-2
m-4
…
3
1
-1
当相差为-1时,快慢指针间的距离变为了m-1。
假设C是环的长度,这里的-1即为C-1;如果环的长度为偶数,那么快慢指针最近的距离为1,因为一次减小的距离为2,所以永远也追不上慢指针。
环形链表(2)
和第一道题不一样的是这道题如果有环,就返回入环的第一个节点,如果链表无环,就返回NULL。
接下来就要进行分析
当快指针与慢指针相遇时,快指针所走的路程是慢指针的两倍。
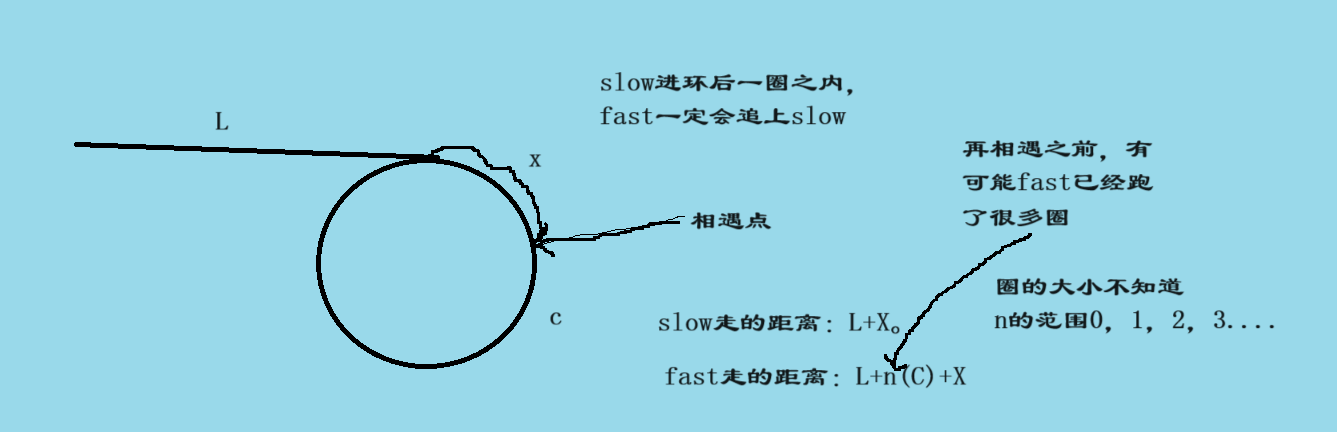
假设起点到入环口的距离是L,圆环的长度为C,入口点到相遇点的距离为x,这时通过分析就可以列出一个等式。
快指针的路程是慢指针的二倍2(L+X)=L+n( C )+X
可得
L+X=n( C )
L=n( C )-X;设置两个指针,第一个指针从起始位置出发,另一个指针从相遇点出发,他们就会在环的入口处相遇。
套用第一道题的思路,快慢指针相遇时找到相遇点,在设置两个指针分别出发,直到相遇,如果没有环的话就返回NULL;
代码如下struct ListNode*fast=head;struct ListNode*slow=head;while(fast&&fast->next){fast=fast->next->next;slow=slow->next;if(slow==fast){struct ListNode*meet=slow;while(head!=meet){head=head->next;meet=meet->next;}return meet;}}return NULL; }提交后顺利通过。
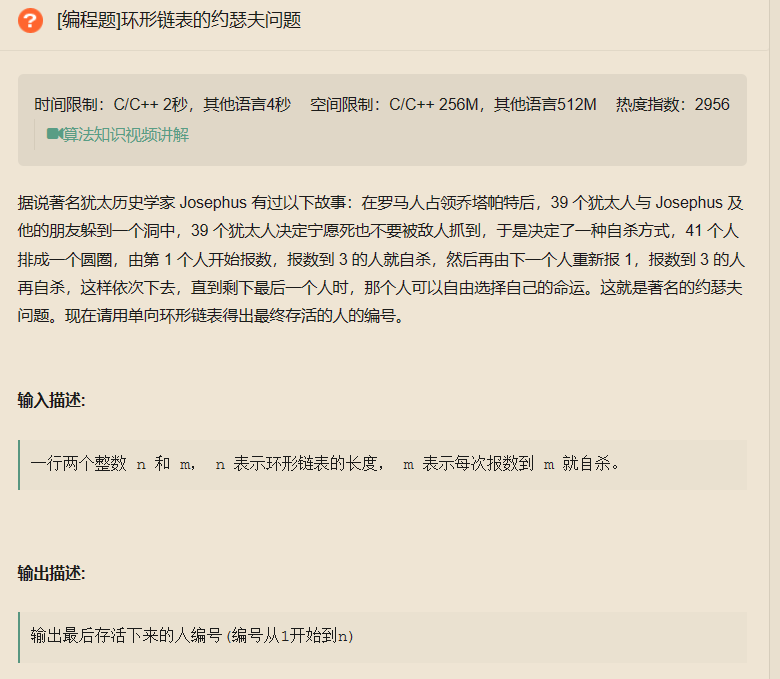
环形链表的约瑟夫问题
链接:
环形链表的约瑟夫问题
要使用单向链表实现。
分析题目,构建一个链表,依次储存节点的位置,然后找到链表的尾,尾的next等于头节点,这样一个环形链表就构建成功了。
从第一个节点开始往后走m-1步(数数时为m,因为第一个节点数1,所以往后走m-1到达目标节点),保存这个节点的next,将起始位置更改为该next,然后从新的起始位置继续往后边数,直到删除到只剩最后一个节点为止,假设这个节点为hei,那么循环结束的条件就是hei->next==hei,判断条件就是hei->next!-hei。
要注意
看代码,讲解很详细
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef struct ListNode
{int val;struct ListNode* next;
}LN;LN* Initnode()
{LN* head = (LN*)malloc(sizeof(LN));head->next = NULL;head->val = 0;return head;
}LN* GetNewnode(int x)
{LN* newnode = (LN*)malloc(sizeof(LN));newnode->next = NULL;newnode->val = x;return newnode;
}
void Pushnode(LN* head, int x)
{assert(head);LN* pre = head;while (pre->next){pre = pre->next;}pre->next = GetNewnode(x);
}void Popnode(LN*head,LN* node)
{LN* cur = head;while (cur->next != node){cur = cur->next;找到要删除的节点的前一个}LN* next = node->next;cur->next = next;free(node);node = NULL;
}int main()
{int m, n;scanf("%d %d", &m, &n);//建立链表LN* head = GetNewnode(1);//第一个编号为1for (int i = 2; i <= m; i++){Pushnode(head, i);//建立链表}//找尾LN* cur = head;while (cur->next != NULL){cur = cur->next;}cur->next = head;//环形链表弄完//数数删位LN* hei = head;while (hei->next != hei){for (int i = 1; i < n; i++)//因为移动三步,是移动量两次。{hei = hei->next;}LN* pop = hei;//找到要删除的节点pophei = hei->next;//更换hei的位置Popnode(hei,pop);//删除pop。}printf("%d ", hei->val);//打印留下的节点的数值。return 0;
}
本文的讲解到这里就结束啦,鄙人才识短浅,如有错误还请多多指教。
相关文章:
力扣环形链表(1)进阶环形链表(2)及环形链表的约瑟夫问题
为了加深对环形链表的理解和掌握,这两道题是很不错的选择。 这里所说环形链表不是一个圈圈的结构,而是带环链表。 链接:环形链表(1) 注意这里链表的长度 所以要注意链表是否为空 第一种方法,应该是比较容易…...

linux文件权限与目录配置
用户与用户组 linux一般将文件可读写的身份分为三个类别:拥有者(owner)、所属群组(group)、其他人(other) 三种身份都有读、写、执行等权限 文件拥有者 linux是个多人多任务的系统,…...
2023年10月wxid转微信号方法
在9月份tx做了一次调整,以前很多wxid转微信号的办法都失效了。 今天分析了一下微信。捣鼓了一下午。现在已经实现了wxid转微信号。不管对方是否在群里,是否是你的好友 都能转。一分钟出60条左右。 我们先创建一个文本文件,将要转换wxid 放进…...

【Spring Boot 源码学习】@Conditional 条件注解
Spring Boot 源码学习系列 Conditional 条件注解 引言往期内容主要内容1. 初识 Conditional2. Conditional 的衍生注解 总结 引言 前面的博文,Huazie 带大家从 Spring Boot 源码深入了解了自动配置类的读取和筛选的过程,然后又详解了OnClassCondition、…...

jupyter_快速开始
文章目录 使用 Anaconda 启动 jupyter-lab纯 python 环境使用 jupyter-notebook纯 python 环境使用 jupyter-labjupyter-lab 配置文件相关jupyter-notebook 配置文件相关jupyter-lab 与 jupyter-notebook 的关系与区别 使用 Anaconda 启动 jupyter-lab 启动一个cmd 命令行&…...
英特尔 SGX 技术概述
目录 介绍概述指示结构Memory安全区页面缓存Enclave Page Cache (EPC)安全区页面缓存映射Enclave Page Cache Map (EPCM) Memory ManagementStructures页面信息Page Information (PAGEINFO)安全信息Security Information (SECINFO)分页加密元数据Paging …...
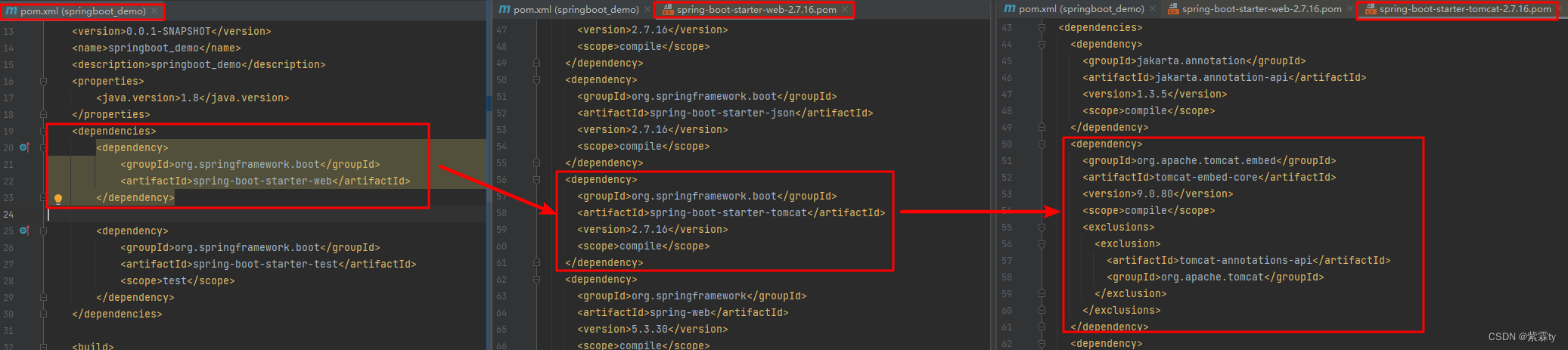
SpringBoot核心功能与基础配置
SpringBoot简介 原先的Spring程序缺点,包括依赖设置繁琐,每项jar的引用都需要自己撰写。并且配置繁琐,配置文件中也需要自己写加载bean等。由此针对原始的Spring程序,Pivotal团队提供的全新框架——SpringBoot,其设计…...
vue3后台管理框架之Mock开发
前言 在前后端对接中,有时后端的接口数据没有 那么快能给出,因此我们可以通过mock模拟自己的请求数据,在后端接口没有给出的同时,先使用mock请求的数据完成前端相关的逻辑 官方文档:vite-plugin-mock vite 的数据模…...

03_51单片机点亮LED灯
51单片机是一种非常常见的单片机型号,广泛应用于各种嵌入式系统和电子设备中。LED灯是一种常见的输出设备,用于显示信息或指示状态。下面是关于51单片机控制LED灯的介绍: 1. 连接LED灯:将LED的正极连接到51单片机的一个I/O引脚&a…...

【前端设计模式】之备忘录模式
备忘录模式是一种行为设计模式,它允许在不破坏封装性的前提下捕获和恢复对象的内部状态。在前端开发中,备忘录模式可以用于保存和恢复用户界面的状态,以及实现撤销和重做功能。 备忘录模式特性: 封装了对象的状态:备…...

复习Day15:栈与队列part02:20. 有效的括号、1047.删除字符串中所有相邻重复项
我用的方法是在leetcode再过一遍例题,明显会的就复制粘贴,之前没写出来就重写,然后从拓展题目中找题目来写。辅以Labuladong的文章看。然后刷题不用CLion了,使用leetcode自带的IDE模拟面试环境。 历史博客链接: http…...

基于Java的宠物商城管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

Python的GIL存在的情况下,是否还有必要添加线程锁。
GIL锁的产生: 为了保证在单线程情况下,Python的正常执行和效率,GIL锁产生了,由于只有一把锁就不会产生死锁也不用切换。 对于Python语言而言,只有CPython解释器(用C语言编写的Python解释库)存在…...
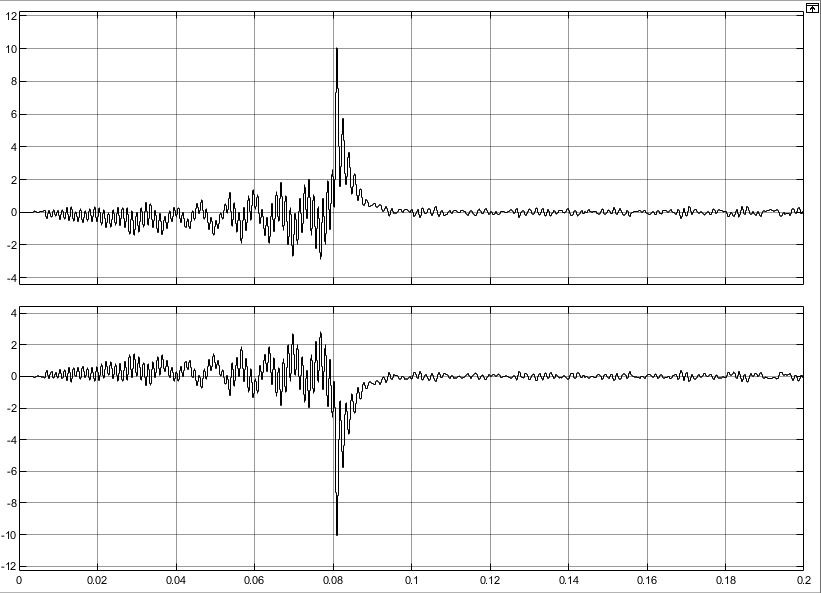
基于下垂控制的孤岛双机并联逆变器环流抑制MATLAB仿真模型
微❤关注“电气仔推送”获得资料(专享优惠) 在实际应用中逆变器都是并联运行的,但是逆变器的并联运行也存在不少问题,由于线路阻抗差异、各个逆变器输出端瞬时电压幅值不同等,都容易导致环流的出现。环流会导致逆变器损耗增加,从而影响微电网的输出效率…...

spring事务面试题
1.Spring 事务实现方式有哪些? 事务就是一系列的操作原子操作,Spring事务机制主要 包括声明式事务和编程式事务。 编程式事务:通过编程的方式管理事务,自己设置未提交模式,自己获取连接,自己预编译,自己回…...

C++标准库算法整理
目录 1、数值操作 1.1、std::accumulate 1.2、std::inner_product 1.3、std::partial_sum 1.4、std::exclusive_scan 1.5、std::inclusive_scan 1.6、std::reduce 2、相邻元素 2.1、std::adjacent_difference 2.2、std::adjacent_find 2.3、std::unique 2.4、std::u…...
【待补】)
【Codeforces】Codeforces Round 903 (Div. 3)【待补】
Dashboard - Codeforces Round 903 (Div. 3) - Codeforces Problem - C - Codeforces Problem - D - Codeforces...
)
workerman 运行时报错 Call to undefined function posix_getpid()
使用 验证php扩展是否齐全 curl -Ss https://www.workerman.net/check | php缺少posix 下载 在 Linux 系统上,可以使用包管理器来安装 php-posix 扩展,例如 Ubuntu 系统可以通过以下命令进行安装: sudo apt-get install php-posix如果你使用…...

【探讨C++中的临时对象:一时之物还是永恒之道?】
在C编程中,临时对象是一个经常引起讨论的话题。它们是什么,为什么它们存在,以及如何正确使用它们?本文将深入探讨C中的临时对象,帮助您理解它们的含义和用途。 什么是临时对象? 临时对象(Temp…...
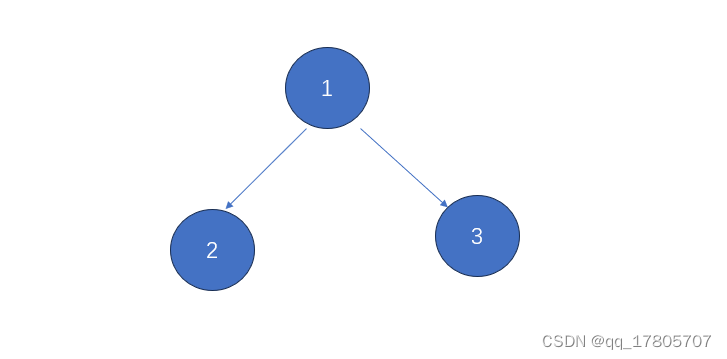
二叉树相关算法
1、二叉树基本操作 二叉树的定义就不在这里多说了,下面这个图就是一个简单的二叉树: 二叉树的三种遍历方式: 前序遍历:头左右,也就是先头后左再右:1245367 public static void prePrint(BinaryTreeNode …...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
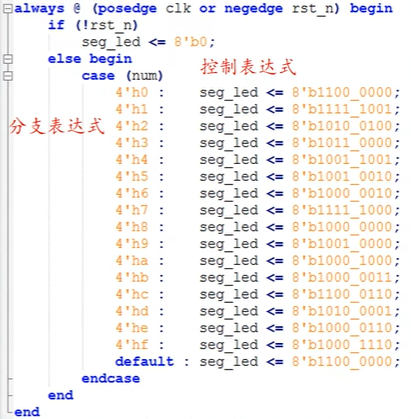
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...