【LeetCode热题100】--287.寻找重复数
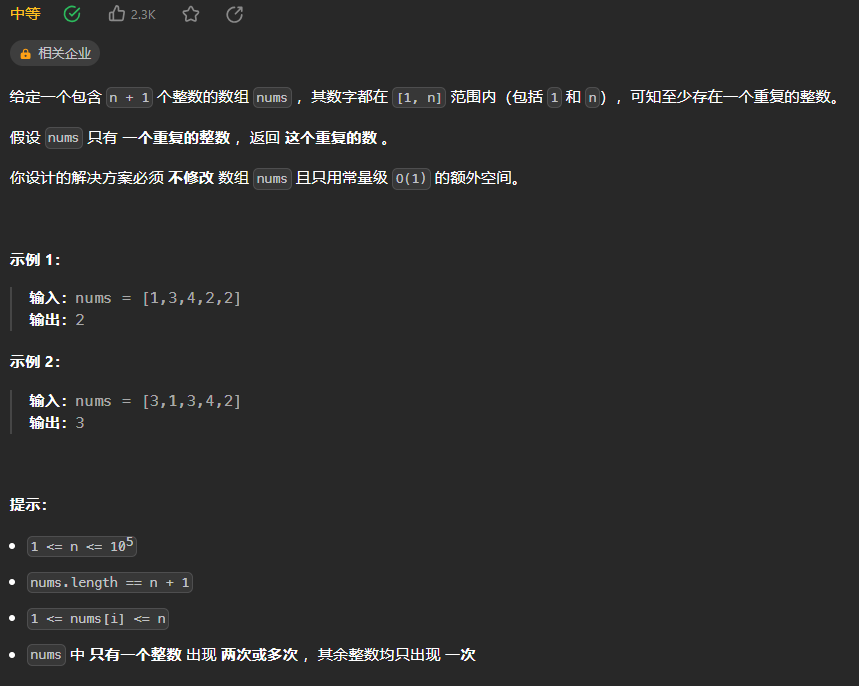
287.寻找重复数
方法:使用快慢指针
使用环形链表II的方法解题(142.环形链表II),使用 142 题的思想来解决此题的关键是要理解如何将输入的数组看作为链表。 首先明确前提,整数的数组 nums 中的数字范围是 [1,n]。考虑一下两种情况:
- 如果数组中没有重复的数,以数组 [1,3,4,2]为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n), 其映射关系 n->f(n)为: 0->1 1->3 2->4 3->2 我们从下标为 0 出发,根据 f(n)计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推,直到下标超界。这样可以产生一个类似链表一样的序列。 0->1->3->2->4->null
- 如果数组中有重复的数,以数组 [1,3,4,2,2] 为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n), 其映射关系 n->f(n) 为: 0->1 1->3 2->4 3->2 4->2 同样的,我们从下标为 0 出发,根据 f(n)f(n)f(n) 计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推产生一个类似链表一样的序列。 0->1->3->2->4->2->4->2->…… 这里 2->4 是一个循环,那么这个链表可以抽象为下图:

从理论上讲,数组中如果有重复的数,那么就会产生多对一的映射,这样,形成的链表就一定会有环路了,
综上 1.数组中有一个重复的整数 <–> 链表中存在环 2.找到数组中的重复整数 <–> 找到链表的环入口
至此,问题转换为 142 题。那么针对此题,快、慢指针该如何走呢。根据上述数组转链表的映射关系,可推出 142 题中慢指针走一步 slow = slow.next ==> 本题 slow = nums[slow] 142 题中快指针走两步 fast = fast.next.next ==> 本题 fast = nums[nums[fast]]
class Solution {/*** 287.数组nums有n+1个整数,均位于[1,n]内,可知至少存在一个重复整数;假设nums中只有一个重复整数,找出该整数* 要求:不能修改nums且空间复杂度为O(1)* 方法:根据nums构造链表,链表中每个节点既表示nums中下标,又表示nums中值* 如[1,3,4,2]对应链表:0->1->3->2->4* nums对应的链表中,每个节点的出度都为1,因为nums.length == n+1,所以nums[n]是存在的,* 进而链表中第n个节点(尾结点)又会指向一个前驱节点,必定形成环* 对于[1,3,4,2,2],链表尾的4号节点又会指向2号节点,形成环,2号节点是环的入口,* 其入度又为2,代表着nums中出现了两次2这个取值,因此2就是重复整数* 现在,问题就转化成了142题的环形链表入口检测问题* */public int findDuplicate(int[] nums) {int n = nums.length - 1;int slow = 0, fast = 0;slow = nums[slow]; // 对于本题, slow = slow.next对应于slow = nums[slow]fast = nums[nums[fast]]; // fast = fast.next.next对应于fast = nums[nums[fast]]// 第一阶段:slow与fast相遇,判断成环while (slow != fast) {slow = nums[slow];fast = nums[nums[fast]];}// 第二阶段:找到入环点// slow与fast相遇时,假设slow走过的路程是l+b,其中l是slow入环前走过的路程,b是slow入环后走过的路程// 假设环的长度为r,则fast走过的路程可以表达为2(l+b)=l+b+k*r,整理后可得l=k*r-b// 上述等式意味着,若一个指针p1从链表头开始前进,当他到达环的入口时(走过l的路程),// 另一个从slow与fast相遇的位置出发的指针p2也回到了环的入口(走过l=k*r-b的路程),此时二者第一次相遇// 因此设置这样两个指针,当p1与p2第一次相遇,即找到了环的入口int p1 = 0, p2 = slow;while (p1 != p2) {p1 = nums[p1];p2 = nums[p2];}return p1;}
}
相关文章:

【LeetCode热题100】--287.寻找重复数
287.寻找重复数 方法:使用快慢指针 使用环形链表II的方法解题(142.环形链表II),使用 142 题的思想来解决此题的关键是要理解如何将输入的数组看作为链表。 首先明确前提,整数的数组 nums 中的数字范围是 [1,n]。考虑一…...
)
JUC并发编程——Stream流式计算(基于狂神说的学习笔记)
Stream流式计算 什么是Stream流式计算 Stream流式计算是一种基于数据流的计算模式,它可以对数据进行实时处理和分析,而不需要将所有数据存储在内存中。 Stream流式计算是将数据源中的数据分割成多个小的数据块,然后对每个小的数据块进行并…...
【Eclipse】取消按空格自动补全,以及出现没有src的解决办法
【Eclipse】设置自动提示 教程 根据上方链接,我们已经知道如何设置Eclipse的自动补全功能了,但是有时候敲变量名的时候按空格,本意是操作习惯,不需要自动补全,但是它却给我们自动补全了,这就造成了困扰&…...

ps制作透明公章 公章变透明 ps自动化批量抠图制作透明公章
ps制作透明公章 公章变透明 ps自动化批量抠图制作透明公章 1、抠图制作透明公章2、ps自动化批量抠图制作透明公章 1、抠图制作透明公章 抠图过程看视频 直接访问视频连接可以选高清画质 https://live.csdn.net/v/335752 ps抠图制作透明公章 2、ps自动化批量抠图制作透明公章 …...

Fetch与Axios数据请求
什么是Polyfill? Polyfill是一个js库,主要抚平不同浏览器之间对js实现的差异。比如,html5的storage(session,local), 不同浏览器,不同版本,有些支持,有些不支持。Polyfill(Polyfill有很多,在Gi…...
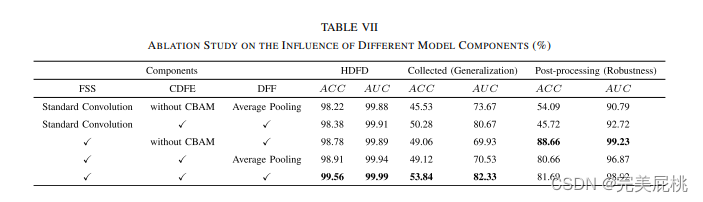
论文阅读-FCD-Net: 学习检测多类型同源深度伪造人脸图像
一、论文信息 论文题目:FCD-Net: Learning to Detect Multiple Types of Homologous Deepfake Face Images 作者团队:Ruidong Han , Xiaofeng Wang , Ningning Bai, Qin Wang, Zinian Liu, and Jianru Xue (西安理工大学,西安交…...
云服务器快速搭建网站
目录 安装Apache Docker 安装 Mysql 安装 Docker 依赖包 添加 Docker 官方仓库 安装 Docker 引擎 启动 Docker 服务并设置开机自启 验证 Docker 是否成功安装 拉取 MySQL 镜像 查看本地镜像 运行容器 停止和启动容器 列出正在运行的容器 安装PHP环境 搭建网站 安装…...

小程序首页搭建
小程序首页搭建 1. Flex布局是什么?2. 容器的属性2.1 flex-direction属性2.2 flex-wrap属性2.3 flex-flow属性2.4 justify-content属性2.5 align-items属性2.6 align-content属性 二.首页布局搭建二.1moke模拟数据实现轮播图4.信息搭建 Flex弹性布局 1. Flex布局是…...
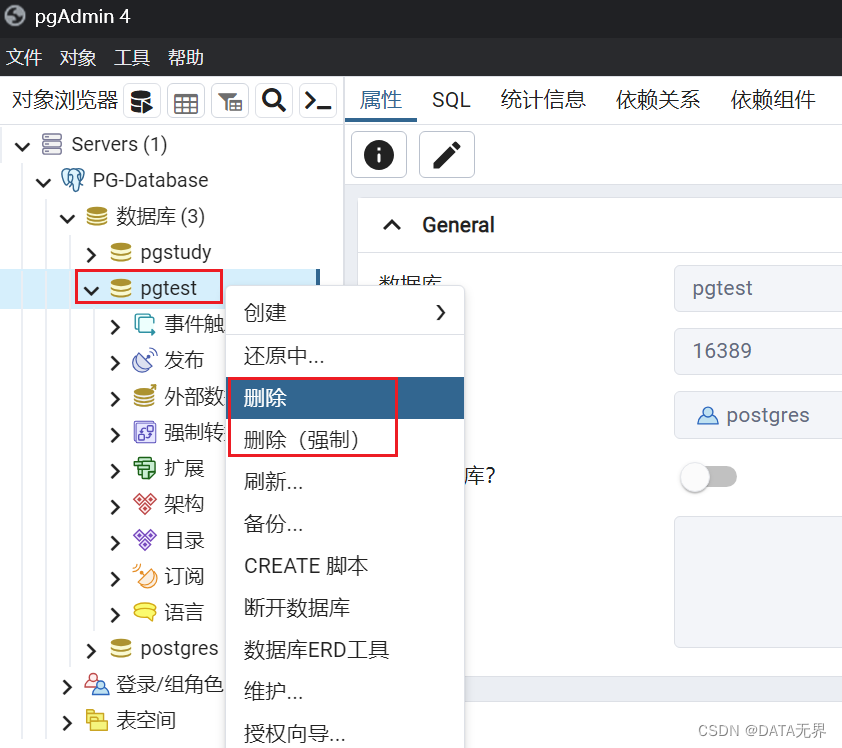
5、使用 pgAdmin4 图形化创建和管理 PostgreSQL 数据库
通过上几篇文章我们讲解了如何安装 PostgreSQL 数据库软件和 pgAdmin4 图形化管理工具。 今天我们继续学习如何通过 pgAdmin4 管理工具图形化创建和管理 PostgreSQL 数据库。 一、PostgreSQL的基本工作方式 在学习如何使用PostgreSQL创建数据库之前,我们需要了解一…...

EtherCAT转Modbus-TCP协议网关与DCS连接的配置方法
远创智控YC-ECTM-TCP,自主研发的通讯网关,将为你解决以太网通讯难题。YC-ECTM-TCP是一款EtherCAT主站功能的通讯网关,能够将EtherCAT网络和Modbus-TCP网络连接起来。它可以作为EtherCAT网络中的主站使用,同时也可以作为Modbus-TCP…...

合伙企业的执行事务合伙人委派代表是什么样的存在
当合伙企业的执行事务合伙人为法人或非法人组织时,通常会委派自然人代表其执行合伙事务,特别是各类投资基金、信托、资产证券化等合伙企业类型的SPV中,由法人执行事务合伙人委派代表执行合伙企业事务比较常见,由此可能出现合伙企业…...
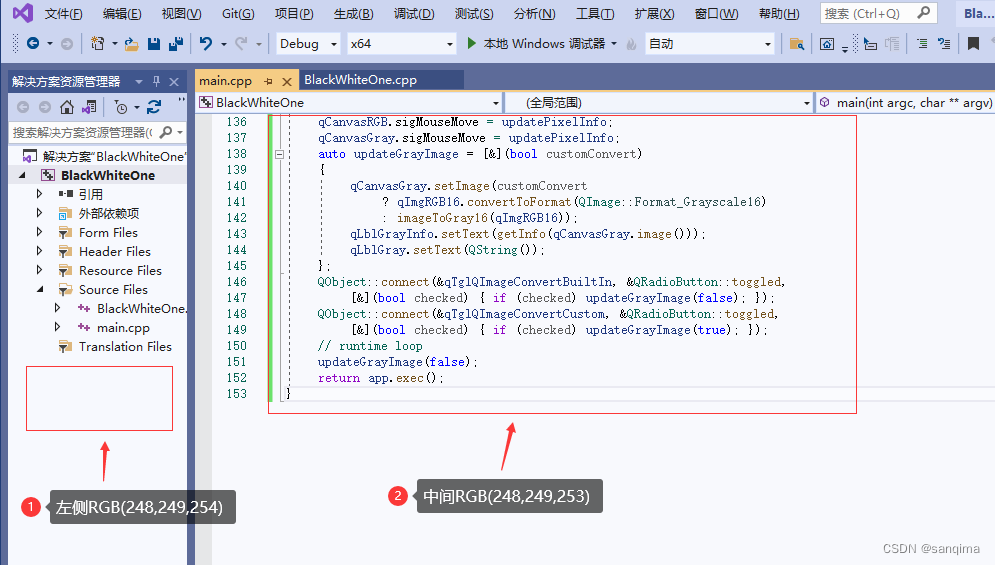
visual studio设置主题和背景颜色
visual studio2019默认的主题有4种,分别是浅白色、深黑色、蓝色、蓝(额外对比度),背景颜色默认是纯白色RGB(255,255,255)。字体纯白色看久了,眼睛会感到酸痛、疲劳,建议改成浅白RGB(250,250,250)、豆沙绿RGB(85,123,105)、透明蓝白…...

[JVM]问下,对象在堆上的内存分配是怎样的
Java 技术体系的自动内存管理,最根本的目标是自动化地解决两个问题:自动给对象分配内存以及自动回收分配给对象的内存 这里面最重要的就是,对象在堆上的内存分配 这篇文章来具体讲讲 堆整体上来说,主要分为 新生代 & 老年代 新生代又分为: Eden 区和 Survivor 区, Survivo…...
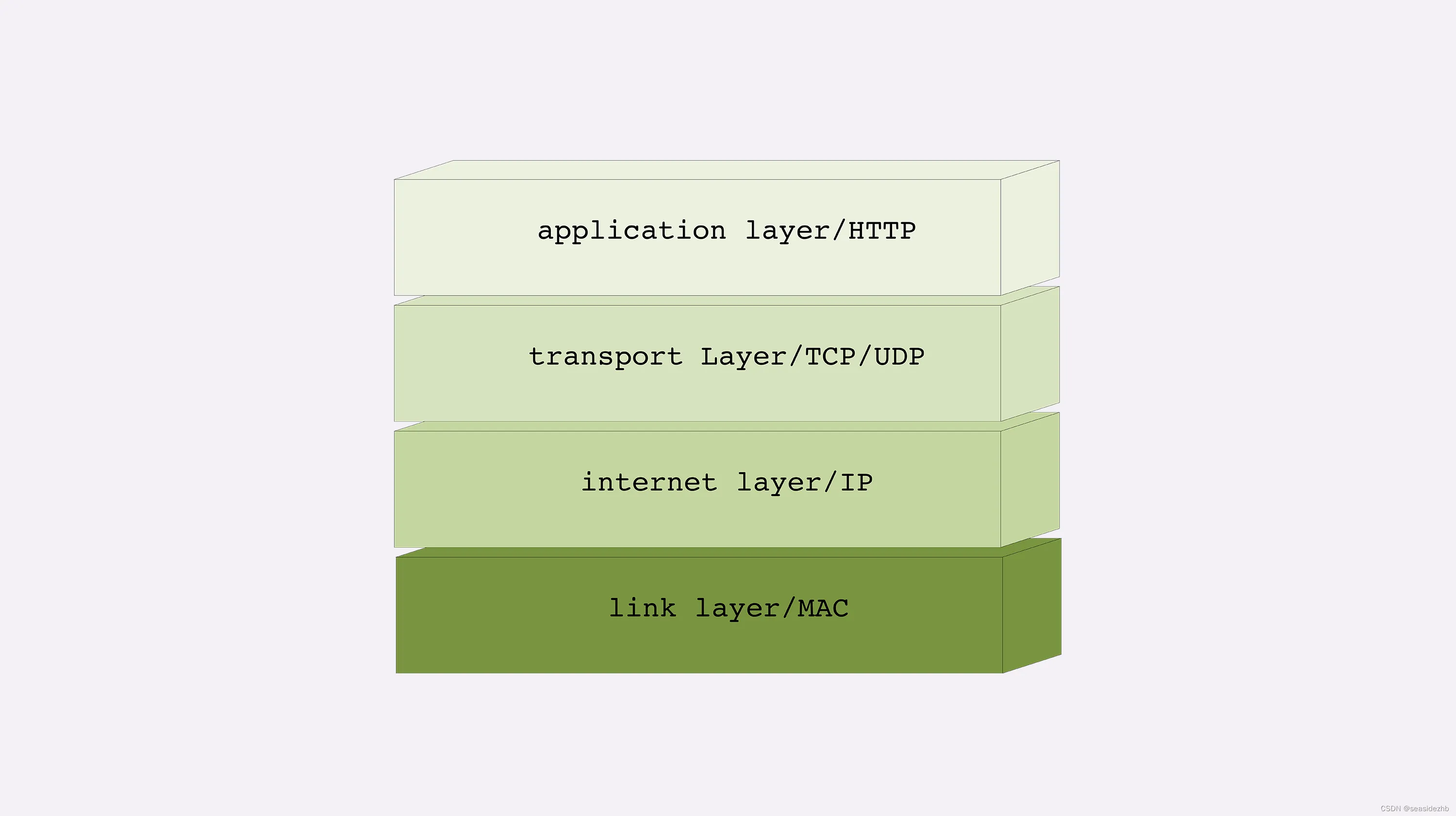
TCP/IP网络分层模型
TCP/IP当初的设计者真的是非常聪明,创造性地提出了“分层”的概念,把复杂的网络通信划分出多个层次,再给每一个层次分配不同的职责,层次内只专心做自己的事情就好,用“分而治之”的思想把一个“大麻烦”拆分成了数个“…...

数据结构-----红黑树的插入
目录 前言 红黑树的储存结构 一、节点旋转操作 左旋(Left Rotation) 右旋(Right Rotation) 二、插入节点 1.插入的是空树 2.插入节点的key重新重复 3.插入节点的父节点是黑色 4.插入节点的父节点是红色 4.1父节点是祖父…...
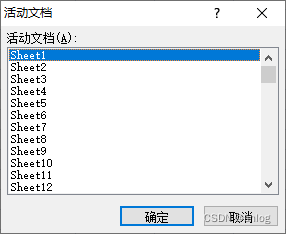
Excel大量表格选择,快速定位表格
excel有大量表格,快速定位表格方法。 在这个区域电机鼠标右键 出现表格选择。(此处方便查看15个表格),如果超过15个表格可以选择其他工资表。 选择其他工作表会弹出列表框如下图 特此记录 anlog 2023年10月12日...
力扣环形链表(1)进阶环形链表(2)及环形链表的约瑟夫问题
为了加深对环形链表的理解和掌握,这两道题是很不错的选择。 这里所说环形链表不是一个圈圈的结构,而是带环链表。 链接:环形链表(1) 注意这里链表的长度 所以要注意链表是否为空 第一种方法,应该是比较容易…...

linux文件权限与目录配置
用户与用户组 linux一般将文件可读写的身份分为三个类别:拥有者(owner)、所属群组(group)、其他人(other) 三种身份都有读、写、执行等权限 文件拥有者 linux是个多人多任务的系统,…...
2023年10月wxid转微信号方法
在9月份tx做了一次调整,以前很多wxid转微信号的办法都失效了。 今天分析了一下微信。捣鼓了一下午。现在已经实现了wxid转微信号。不管对方是否在群里,是否是你的好友 都能转。一分钟出60条左右。 我们先创建一个文本文件,将要转换wxid 放进…...

【Spring Boot 源码学习】@Conditional 条件注解
Spring Boot 源码学习系列 Conditional 条件注解 引言往期内容主要内容1. 初识 Conditional2. Conditional 的衍生注解 总结 引言 前面的博文,Huazie 带大家从 Spring Boot 源码深入了解了自动配置类的读取和筛选的过程,然后又详解了OnClassCondition、…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
