数据结构-----红黑树的插入
目录
前言
红黑树的储存结构
一、节点旋转操作
左旋(Left Rotation)
右旋(Right Rotation)
二、插入节点
1.插入的是空树
2.插入节点的key重新重复
3.插入节点的父节点是黑色
4.插入节点的父节点是红色
4.1父节点是祖父节点的左子节点
4.1.1叔叔节点是红色
4.1.2叔叔节点是黑色
4.1.2-1 插入节点是作左子节点
4.1.2-2插入节点是作右子节点
4.2父节点是祖父节点的右子节点
4.2.1叔叔节点是红色
4.2.2 叔叔节点是黑色
4.2.1-1 插入节点是作左子节点
4.2.1-2 插入节点是作右子节点
三、完整代码展示
前言
上一期我们初步学习了红黑树的基本概念和特性(上一期链接:数据结构-----红黑树简介_Gretel Tade的博客-CSDN博客 如果不了解红黑树相关性质的话建议看看这个),那么从这一期开始,我们就进入到了红黑树的深入学习,首先我通过这一期来详细介绍红黑树的插入操作实现,下面就看看怎么去把数据插入到红黑树吧!
红黑树的储存结构
根据红黑树的要求,我们可以去定义红黑树节点和树的结构体,如下所示:
//宏定义颜色
#define red 0
#define black 1//数据类型Datatype
typedef char Datatype;
//红黑树节点存储结构
typedef struct node {Datatype data;int color;int key;//排序键值,根据key大小排序struct node* par;//父节点指针struct node* left, * right;//左右子节点指针
}Node;//红黑树的定义rbtree
typedef struct tree {Node* root;//指向根节点指针Node* nil;//叶子节点(哨兵)
}rbtree;一、节点旋转操作
在数据结构当中,旋转操作是一种很常见的操作,可能去实现数据结构平衡或者其他相关特性的要求,同样的的AVL树和红黑树里边也是要进行旋转操作的,通过旋转来满足平衡的特性。旋转分两种:左旋(Left Rotation)和右旋(Right Rotation)
左旋(Left Rotation)
左旋是一种将某个节点的右子节点旋转上来的操作。也就是说当前节点的右子节点顶替了自己,然后自己变为右子节点的左子节点,以保持树的平衡。
操作如下:
- 将当前节点的右子节点设为新的父节点。
- 将新的父节点的左子节点设为当前节点的右子节点。
- 如果当前节点有父节点,将新的父节点替代当前节点的位置。
- 将当前节点设为新的父节点的左子节点。
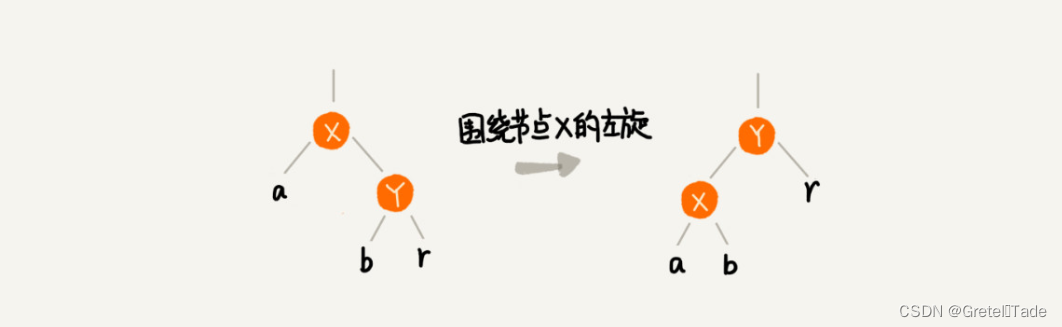 代码实现:
代码实现:
//左旋(以x为旋转点,向左旋转)
void left_rotate(rbtree* T, Node* x) {Node* y = x->right;//标记到右子节点x->right = y->left;//y的左子节点代替x的右子节点if (x->right != T->nil)x->right->par = x;//如果不为空(nil)其父节点指向xy->par = x->par;//把y的父节点指向x的父节点,此时x与y没有直接联系了if (x->par == T->nil) {//判断x的父节点是否为根结点T->root = y;//如果是的话,y就变为根结点}else {//y顶替x的位置if (x == x->par->left)x->par->left = y;//如果x是父节点的左边,那y就代替x成为左子节点elsex->par->right = y;//如果x是父节点的右边,那y就代替x成为右子节点}//y的左子节点指向x,x的父节点指向yy->left = x;x->par = y;
}右旋(Right Rotation)
同样的右旋也是将左子节点顶替自己成为父节点, 然后自己成为左子节点的右子节点。
操作如下:
- 将当前节点的左子节点设为新的父节点
- 将新的父节点的右子节点设为当前节点的左子节点
- 如果当前节点有父节点,将新的父节点替代当前节点的位置
- 将当前节点设为新的父节点的右子节点
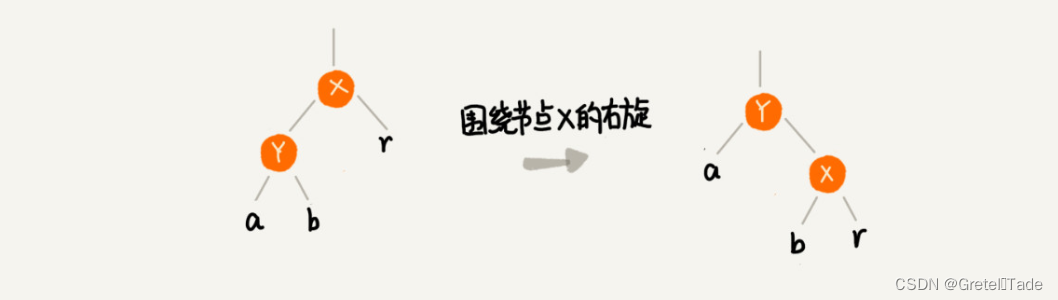
代码实现:
//右旋(以x为旋转点,向右旋转)
void right_rotate(rbtree* T, Node* x) {Node* y = x->left;//标记到左子节点yx->left = y->right;//y的右子节点代替x的左子节点if (x->left != T->nil)x->left->par = x;y->par = x->par;//y的父节点指向x的父节点if (x->par == T->nil)T->root = y;//如果x是根结点的话,那么y代替x成为根结点else {if (x == x->par->left)x->par->left = y;elsex->par->right = y;}//y的右子节点指向x,x的父节点为yy->right = x;x->par = y;
}二、插入节点
再讲之前,我分享一个网址给大家(链接:Red/Black Tree Visualization),这个是一个红黑树模拟器的网址,你们可以去进行红黑树插入删除遍历等操作,可以自己试试看。如下图所示:
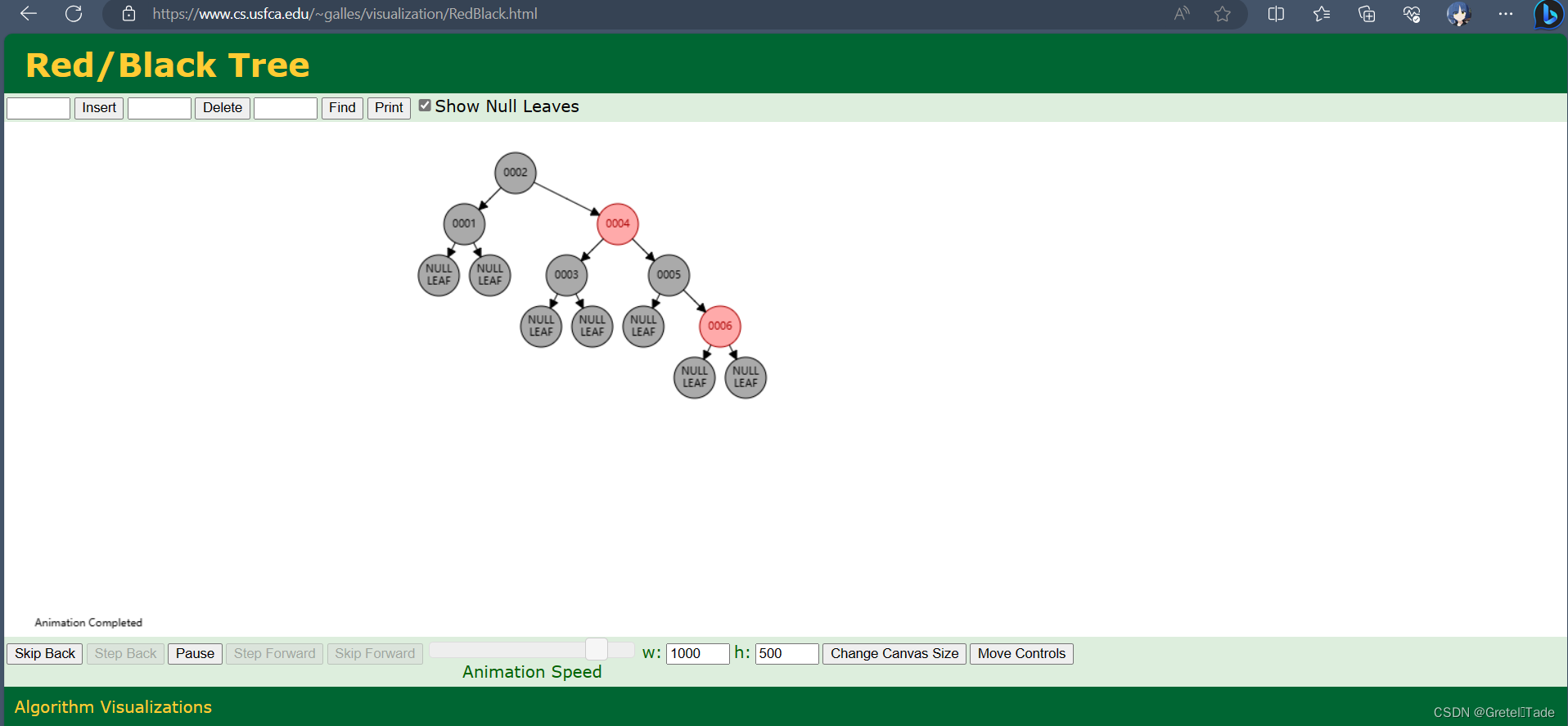 废话不多说了,上正文!
废话不多说了,上正文!
红黑树的插入操作分两步走:
- 找到插入位置
- 进行自平衡调整
注意:插入节点初始为红色
原因分析:因为红黑树中任意一个节点到叶子节点路径所含黑色节点数量相同,也就是说如果我插入的节点为黑色的话,那么就会破坏红黑树的要求,所以插入的节点必须是红色节点,才能保证红黑树的性质。
下面就开始讨论红黑树的几种插入情况:
1.插入的是空树
这是最简单的插入情况,当插入第一个节点的时候,红黑树为空我们只需要让根节点指向这个节点即可。操作如下:
- 根节点指向此节点
- 把根节点染黑
2.插入节点的key重新重复
这种情况的话我们可以根据自己喜好去处理,如果出现了重复的key,那么就把这个key里面的值进行更新;或者我们不进行插入操作,因为key不可以重复,直接退出插入操作。
3.插入节点的父节点是黑色
这很好处理,直接插入就行了,因为父节点为黑色,插入节点为红色,所以不会影响红黑树的平衡性。
- 直接插入即可
4.插入节点的父节点是红色
这种情况是最为复杂的,由于父节点颜色是红色,所以要进行平衡调整,所以要去进一步的讨论才行。那具体根据什么去调整呢?是看叔叔节点的颜色来调整(父节点的兄弟节点),具体分以下几种情况:

大的有两种情况,要看父节点是祖父节点的左边还是右边,下面我就以父节点为左子节点为例子:
下文图标说明:
t 表示插入的节点
P表示父节点
B表示叔叔节点
PP表示祖父节点
4.1父节点是祖父节点的左子节点
4.1.1叔叔节点是红色
如果叔叔节点的颜色是红色的话,这里不需要进行旋转操作,只需要让父节点和叔叔节点颜色变为黑色,祖父节点颜色变为红色即可。流程如下:
- 把P 和B 节点染黑
- 把PP节点染红
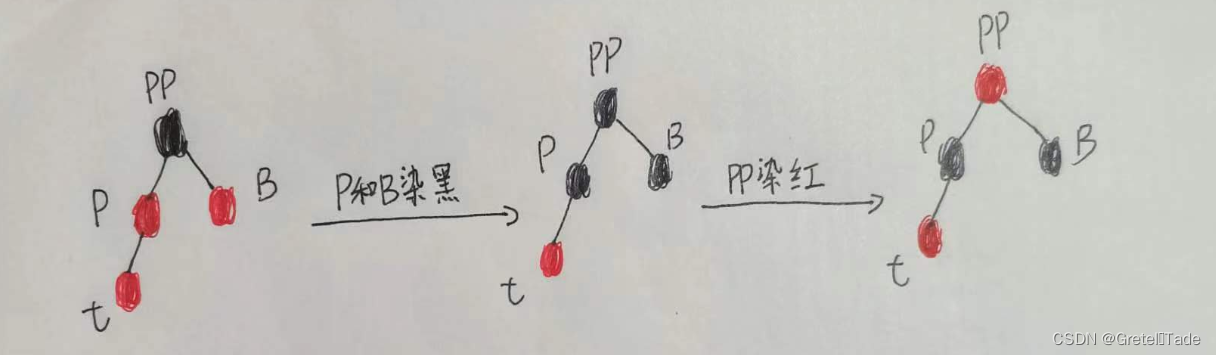
4.1.2叔叔节点是黑色
这里的话又要去分两种情况:
- 插入节点是父节点的左子节点
- 插入节点是父节点的右子节点
4.1.2-1 插入节点是作左子节点
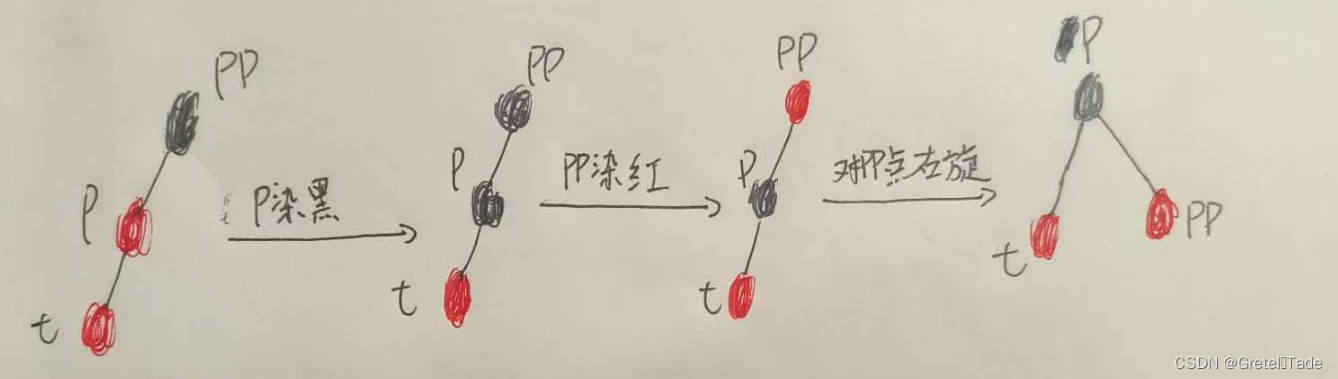
如果插入的节点是父节点的左子节点的话,那么要进行以下操作:
- 把P染黑
- 把PP染红
- 对PP进行右旋
4.1.2-2插入节点是作右子节点
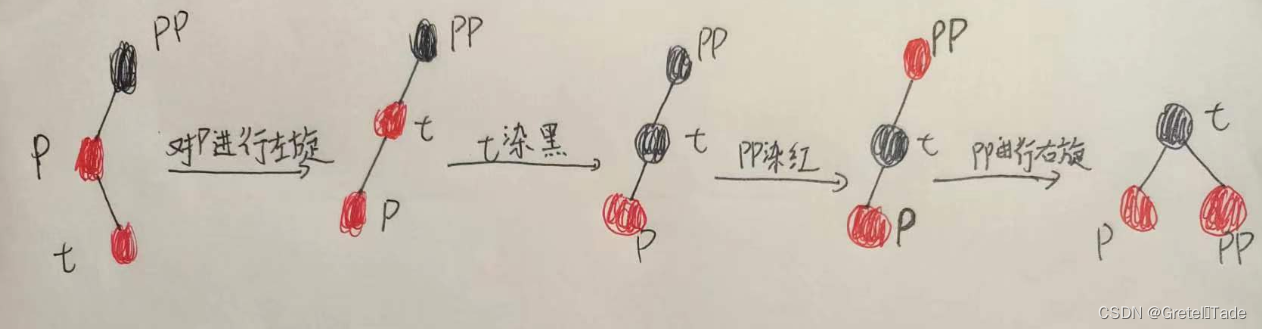
如果插入节点是作为父节点的右子节点的话,要进行以下操作:
- 对P进行左旋
- 把t 染黑
- 把PP染红
- 对PP进行右旋
4.2父节点是祖父节点的右子节点
这里的操作跟4.1基本上是一模一样的,只是对称过去是了,但是我还是想详细列出来吧,下面接着看。
4.2.1叔叔节点是红色
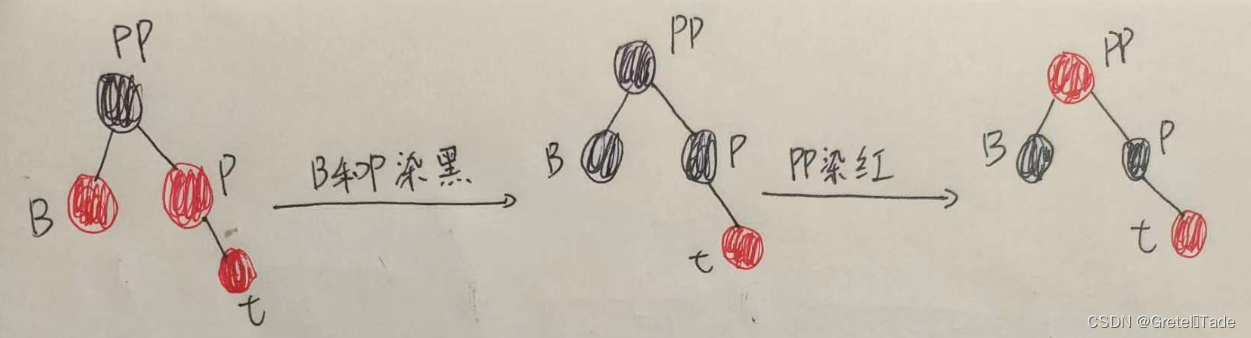
操作步骤如下:
- 把B(叔叔节点)和P(父节点)然黑
- 把PP(祖父节点)染红
4.2.2 叔叔节点是黑色
同样的也是分以下两种情况讨论:
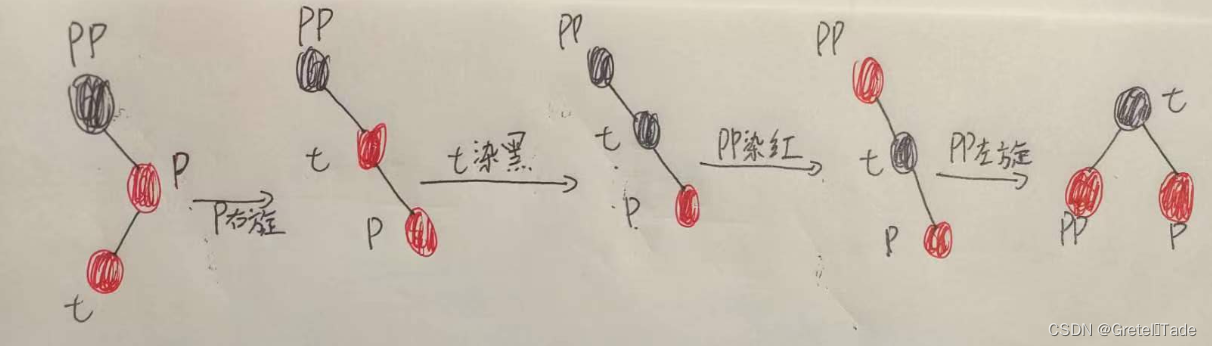
4.2.1-1 插入节点是作左子节点
- 对P 进行右旋
- 将t 染黑
- 将PP 然红
- 对PP 进行左旋
4.2.1-2 插入节点是作右子节点
- 将P 染黑
- 将PP 然红
- 对PP进行左旋
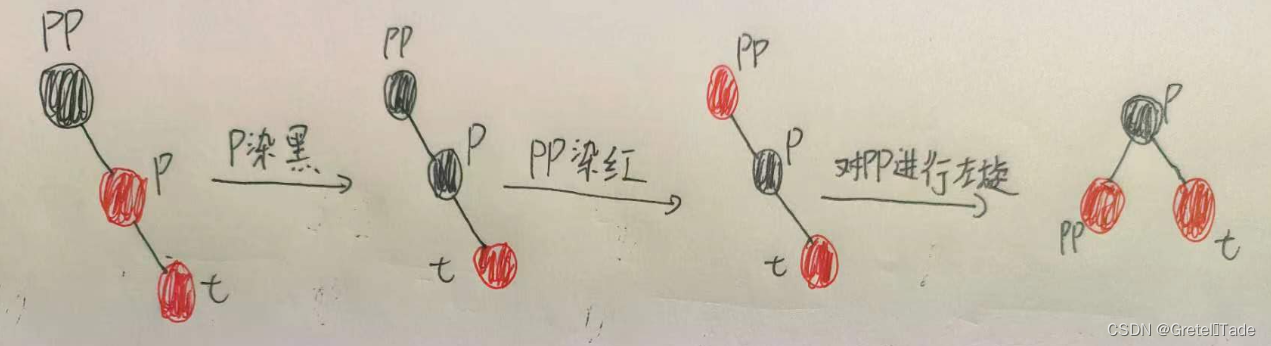
以上这些就是红黑树的插入全部可能了,是不是很多啊,其实还好啦!只要我们把这些情况一个一个分类,然后思路捋一捋很容易弄明白的,后面讲到红黑树的删除还有更多种情况呢!还有就是,这些图片是我自己画的,呃画得不太好,不好意思哈。
三、完整代码展示
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>//宏定义颜色
#define red 0
#define black 1//数据类型Datatype
typedef char Datatype;
//红黑树节点存储结构
typedef struct node {Datatype data;int color;int key;struct node* par;//父节点指针struct node* left, * right;//左右子节点指针
}Node;//红黑树的定义rbtree
typedef struct tree {Node* root;//指向根节点指针Node* nil;//叶子节点(哨兵)
}rbtree;//创建初始化红黑树
rbtree* Create_inittree() {rbtree* T = (rbtree*)malloc(sizeof(rbtree));assert(T);T->nil = (Node*)malloc(sizeof(Node));assert(T->nil);//T->nil是不储存数据的节点,作为空节点代替NULL,也就是哨兵节点(表示空)T->nil->color = black;T->nil->par = NULL;T->nil->left = T->nil->right = NULL;T->root = T->nil;return T;
}//创建一个节点
Node* Create_node(rbtree*T ,Datatype data, int key) {Node* new_node = (Node*)malloc(sizeof(Node));assert(new_node);new_node->data = data;new_node->color = red;//初始化颜色红色//左右父节点为nil哨兵节点new_node->left=new_node->right = T->nil;new_node->par = T->nil;new_node->key = key;return new_node;
}//左旋(以x为旋转点,向左旋转)
void left_rotate(rbtree* T, Node* x) {Node* y = x->right;//标记到右子节点x->right = y->left;//y的左子节点代替x的右子节点if (x->right != T->nil)x->right->par = x;//如果不为空(nil)其父节点指向xy->par = x->par;//把y的父节点指向x的父节点,此时x与y没有直接联系了if (x->par == T->nil) {//判断x的父节点是否为根结点T->root = y;//如果是的话,y就变为根结点}else {//y顶替x的位置if (x == x->par->left)x->par->left = y;//如果x是父节点的左边,那y就代替x成为左子节点elsex->par->right = y;//如果x是父节点的右边,那y就代替x成为右子节点}//y的左子节点指向x,x的父节点指向yy->left = x;x->par = y;
}
//右旋(以x为旋转点,向右旋转)
void right_rotate(rbtree* T, Node* x) {Node* y = x->left;//标记到左子节点yx->left = y->right;//y的右子节点代替x的左子节点if (x->left != T->nil)x->left->par = x;y->par = x->par;//y的父节点指向x的父节点if (x->par == T->nil)T->root = y;//如果x是根结点的话,那么y代替x成为根结点else {if (x == x->par->left)x->par->left = y;elsex->par->right = y;}//y的右子节点指向x,x的父节点为yy->right = x;x->par = y;
}//插入后平衡调整
void Insert_adjust(rbtree* T, Node* t) {//如果父节点的颜色是红色那就进行调整操作了if (t->par->color == red) {Node* p = t->par;Node* pp = p->par;//01 p节点是pp左子节点if (p == pp->left) {Node* uncle = pp->right;//01-1 叔叔节点颜色是红色if (uncle->color == red) {p->color = black;uncle->color = black;pp->color = red;t = pp;}//01-2 叔叔节点颜色是黑色else {//01-2-1 插入节点t是p的左子节点if (t == p->left) {p->color = black;pp->color = red;right_rotate(T, pp);t = p;}//01-2-2 插入节点t是p的右子节点else if(t==p->right){left_rotate(T, p);t->color = black;pp->color = red;right_rotate(T, pp);}}}//02 p节点是pp的右子节点else { Node* uncle = pp->left;//02-1 叔叔节点颜色是红色if (uncle->color == red) {pp->color = red;p->color = black;uncle->color = black;t = pp;}//02-2 叔叔节点颜色是黑色else {//02-2-1 插入节点t是p的右子节点if (t == p->right) {p->color = black;pp->color = red;left_rotate(T,pp);t = p;}//02-2-2 插入节点t是p的左子节点else {right_rotate(T, p);t->color = black;pp->color = red;left_rotate(T, pp);}}}}//根节点标记黑色T->root->color = black;
}//插入节点
void Insert_node(rbtree* T, Datatype data,int key) {assert(T);Node* t = Create_node(T ,data, key);Node* root = T->root;//快指针Node* cur=T->nil;//慢指针//1.如果根节点为空if (T->root==T->nil) {T->root = t;//根结点指向新创建的节点}else {while (root != T->nil) {cur = root;//cur标记为root的上一个节点(父节点)if (t->key > root->key)root = root->right;else if (t->key < root->key)root = root->left;//如果出现插入重复的key值,就退出,不进行插入操作else {printf("Don't insert the same key!\n");free(t);t = NULL;return;}}}//判断插入的位置if (key < cur->key)cur->left = t;//小的话就插入左边elsecur->right = t;//大的话就插入右边t->par = cur;//新插入的父节点指针指向curInsert_adjust(T, t);//平衡调整
}单单值考虑插入操作就有两百多行代码,后面还有删除操作,查找操作,总共的话大概400行代码,这里就先发今天所讲的插入操作内容的代码,注释很详细,慢慢看哈,我相信你一点看得懂的!
以上就是本期的全部内容了,我们下一期讲红黑树的删除操作,下次见!
分享一张壁纸: 
相关文章:

数据结构-----红黑树的插入
目录 前言 红黑树的储存结构 一、节点旋转操作 左旋(Left Rotation) 右旋(Right Rotation) 二、插入节点 1.插入的是空树 2.插入节点的key重新重复 3.插入节点的父节点是黑色 4.插入节点的父节点是红色 4.1父节点是祖父…...
Excel大量表格选择,快速定位表格
excel有大量表格,快速定位表格方法。 在这个区域电机鼠标右键 出现表格选择。(此处方便查看15个表格),如果超过15个表格可以选择其他工资表。 选择其他工作表会弹出列表框如下图 特此记录 anlog 2023年10月12日...
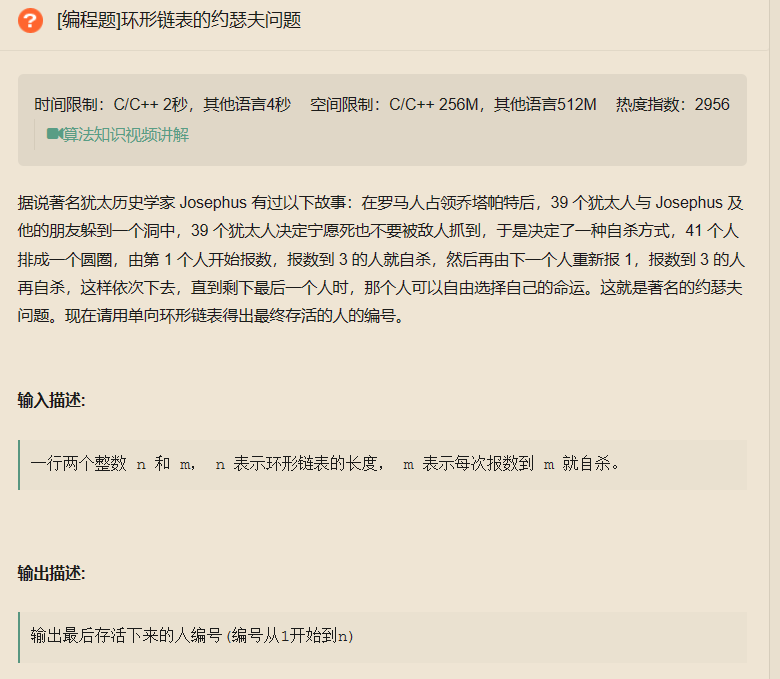
力扣环形链表(1)进阶环形链表(2)及环形链表的约瑟夫问题
为了加深对环形链表的理解和掌握,这两道题是很不错的选择。 这里所说环形链表不是一个圈圈的结构,而是带环链表。 链接:环形链表(1) 注意这里链表的长度 所以要注意链表是否为空 第一种方法,应该是比较容易…...

linux文件权限与目录配置
用户与用户组 linux一般将文件可读写的身份分为三个类别:拥有者(owner)、所属群组(group)、其他人(other) 三种身份都有读、写、执行等权限 文件拥有者 linux是个多人多任务的系统,…...
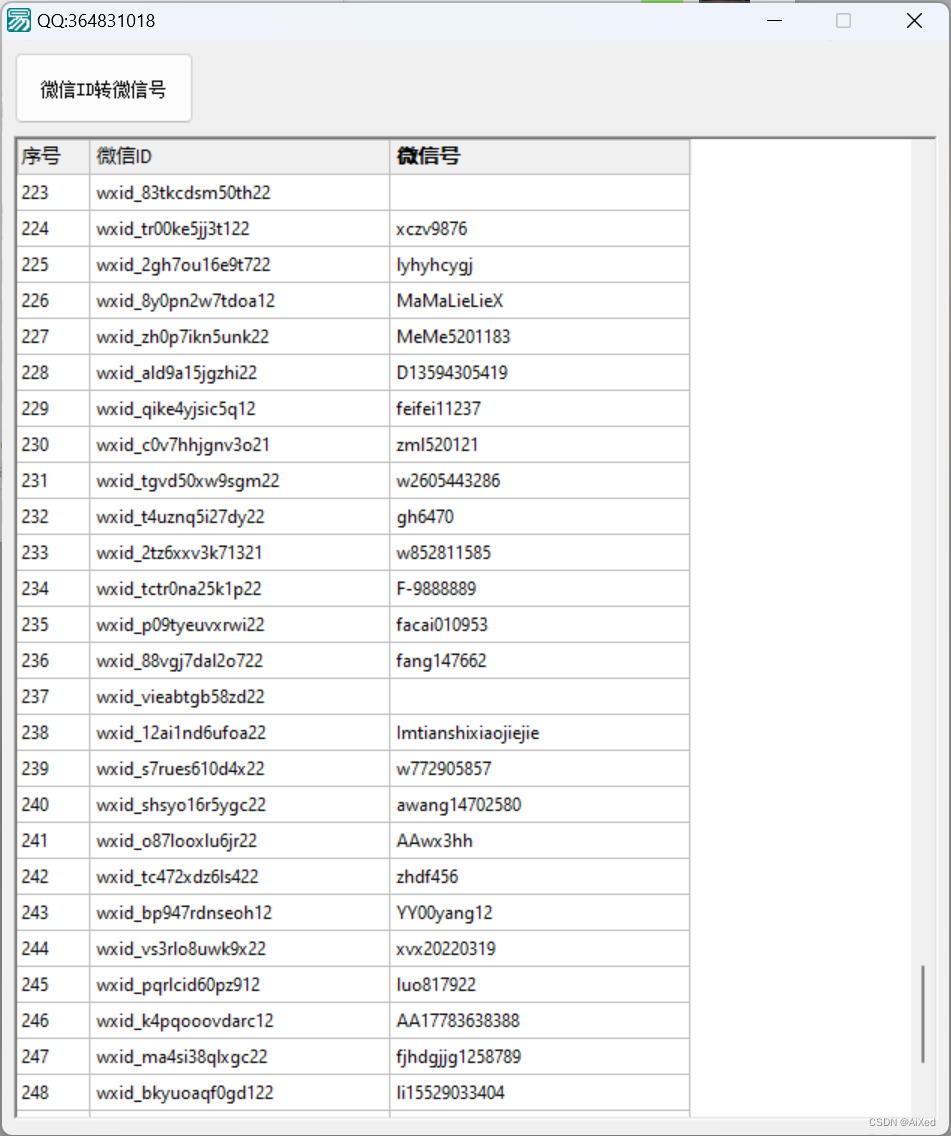
2023年10月wxid转微信号方法
在9月份tx做了一次调整,以前很多wxid转微信号的办法都失效了。 今天分析了一下微信。捣鼓了一下午。现在已经实现了wxid转微信号。不管对方是否在群里,是否是你的好友 都能转。一分钟出60条左右。 我们先创建一个文本文件,将要转换wxid 放进…...

【Spring Boot 源码学习】@Conditional 条件注解
Spring Boot 源码学习系列 Conditional 条件注解 引言往期内容主要内容1. 初识 Conditional2. Conditional 的衍生注解 总结 引言 前面的博文,Huazie 带大家从 Spring Boot 源码深入了解了自动配置类的读取和筛选的过程,然后又详解了OnClassCondition、…...

jupyter_快速开始
文章目录 使用 Anaconda 启动 jupyter-lab纯 python 环境使用 jupyter-notebook纯 python 环境使用 jupyter-labjupyter-lab 配置文件相关jupyter-notebook 配置文件相关jupyter-lab 与 jupyter-notebook 的关系与区别 使用 Anaconda 启动 jupyter-lab 启动一个cmd 命令行&…...
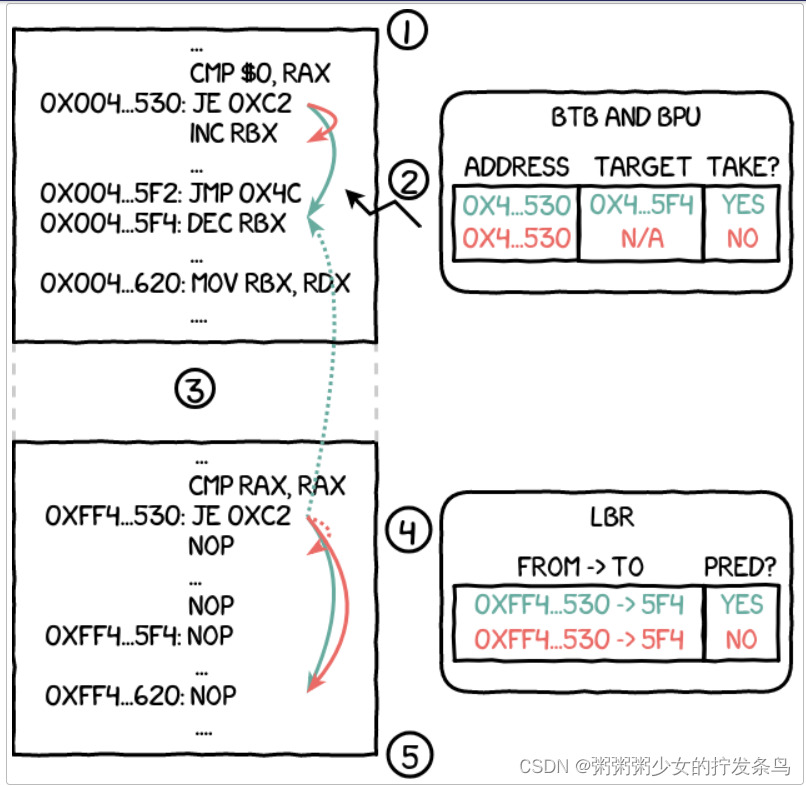
英特尔 SGX 技术概述
目录 介绍概述指示结构Memory安全区页面缓存Enclave Page Cache (EPC)安全区页面缓存映射Enclave Page Cache Map (EPCM) Memory ManagementStructures页面信息Page Information (PAGEINFO)安全信息Security Information (SECINFO)分页加密元数据Paging …...
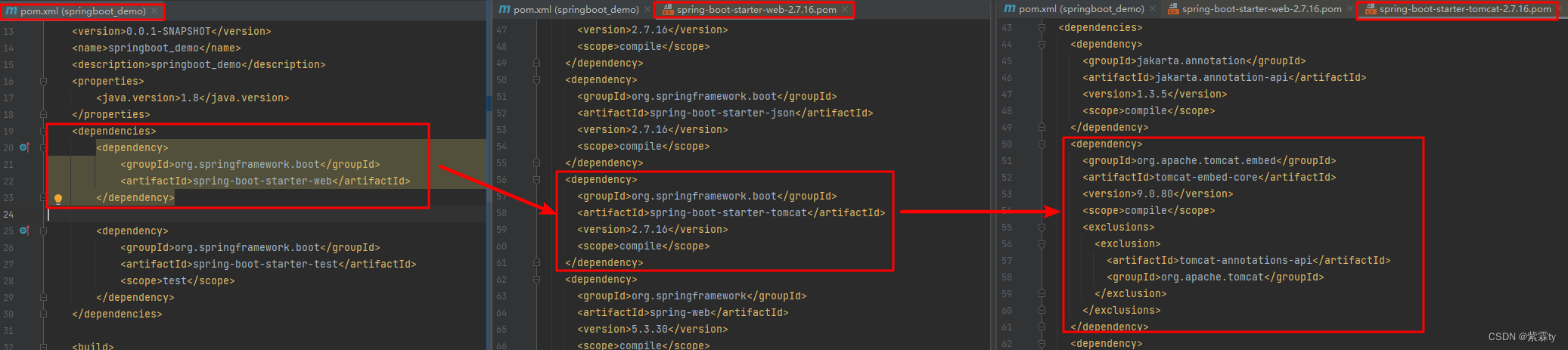
SpringBoot核心功能与基础配置
SpringBoot简介 原先的Spring程序缺点,包括依赖设置繁琐,每项jar的引用都需要自己撰写。并且配置繁琐,配置文件中也需要自己写加载bean等。由此针对原始的Spring程序,Pivotal团队提供的全新框架——SpringBoot,其设计…...
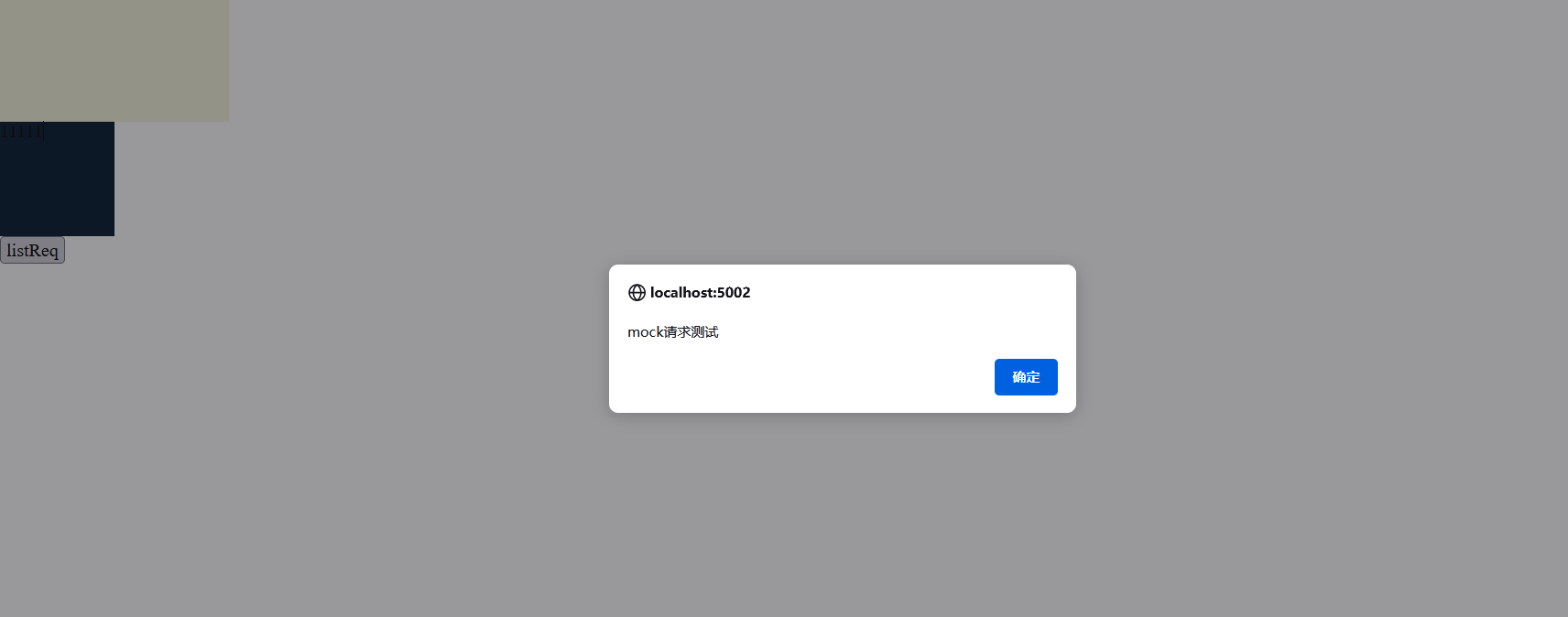
vue3后台管理框架之Mock开发
前言 在前后端对接中,有时后端的接口数据没有 那么快能给出,因此我们可以通过mock模拟自己的请求数据,在后端接口没有给出的同时,先使用mock请求的数据完成前端相关的逻辑 官方文档:vite-plugin-mock vite 的数据模…...

03_51单片机点亮LED灯
51单片机是一种非常常见的单片机型号,广泛应用于各种嵌入式系统和电子设备中。LED灯是一种常见的输出设备,用于显示信息或指示状态。下面是关于51单片机控制LED灯的介绍: 1. 连接LED灯:将LED的正极连接到51单片机的一个I/O引脚&a…...

【前端设计模式】之备忘录模式
备忘录模式是一种行为设计模式,它允许在不破坏封装性的前提下捕获和恢复对象的内部状态。在前端开发中,备忘录模式可以用于保存和恢复用户界面的状态,以及实现撤销和重做功能。 备忘录模式特性: 封装了对象的状态:备…...

复习Day15:栈与队列part02:20. 有效的括号、1047.删除字符串中所有相邻重复项
我用的方法是在leetcode再过一遍例题,明显会的就复制粘贴,之前没写出来就重写,然后从拓展题目中找题目来写。辅以Labuladong的文章看。然后刷题不用CLion了,使用leetcode自带的IDE模拟面试环境。 历史博客链接: http…...

基于Java的宠物商城管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

Python的GIL存在的情况下,是否还有必要添加线程锁。
GIL锁的产生: 为了保证在单线程情况下,Python的正常执行和效率,GIL锁产生了,由于只有一把锁就不会产生死锁也不用切换。 对于Python语言而言,只有CPython解释器(用C语言编写的Python解释库)存在…...
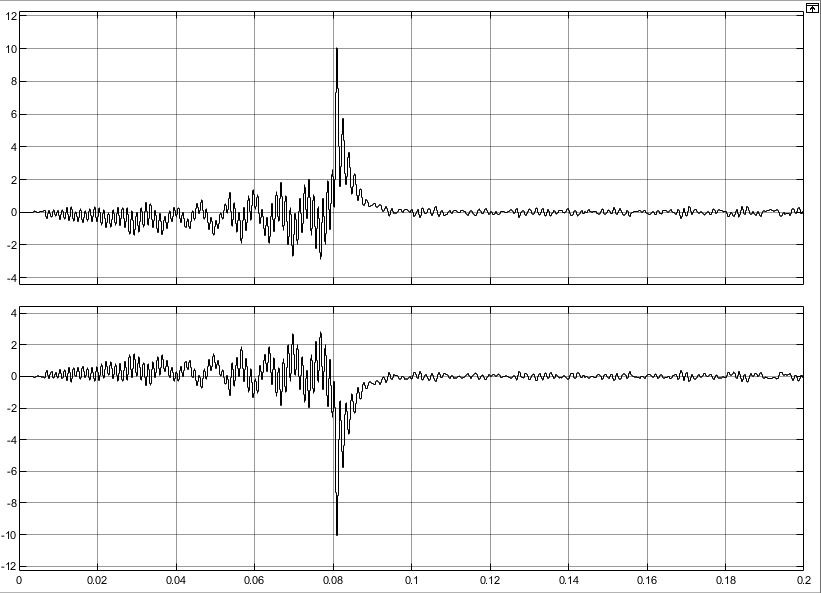
基于下垂控制的孤岛双机并联逆变器环流抑制MATLAB仿真模型
微❤关注“电气仔推送”获得资料(专享优惠) 在实际应用中逆变器都是并联运行的,但是逆变器的并联运行也存在不少问题,由于线路阻抗差异、各个逆变器输出端瞬时电压幅值不同等,都容易导致环流的出现。环流会导致逆变器损耗增加,从而影响微电网的输出效率…...

spring事务面试题
1.Spring 事务实现方式有哪些? 事务就是一系列的操作原子操作,Spring事务机制主要 包括声明式事务和编程式事务。 编程式事务:通过编程的方式管理事务,自己设置未提交模式,自己获取连接,自己预编译,自己回…...

C++标准库算法整理
目录 1、数值操作 1.1、std::accumulate 1.2、std::inner_product 1.3、std::partial_sum 1.4、std::exclusive_scan 1.5、std::inclusive_scan 1.6、std::reduce 2、相邻元素 2.1、std::adjacent_difference 2.2、std::adjacent_find 2.3、std::unique 2.4、std::u…...
【待补】)
【Codeforces】Codeforces Round 903 (Div. 3)【待补】
Dashboard - Codeforces Round 903 (Div. 3) - Codeforces Problem - C - Codeforces Problem - D - Codeforces...
)
workerman 运行时报错 Call to undefined function posix_getpid()
使用 验证php扩展是否齐全 curl -Ss https://www.workerman.net/check | php缺少posix 下载 在 Linux 系统上,可以使用包管理器来安装 php-posix 扩展,例如 Ubuntu 系统可以通过以下命令进行安装: sudo apt-get install php-posix如果你使用…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...
