Kafka SASL认证授权(五)ACL源码解析
Kafka SASL认证授权(五)ACL源码解析。
官网地址:https://kafka.apache.org/
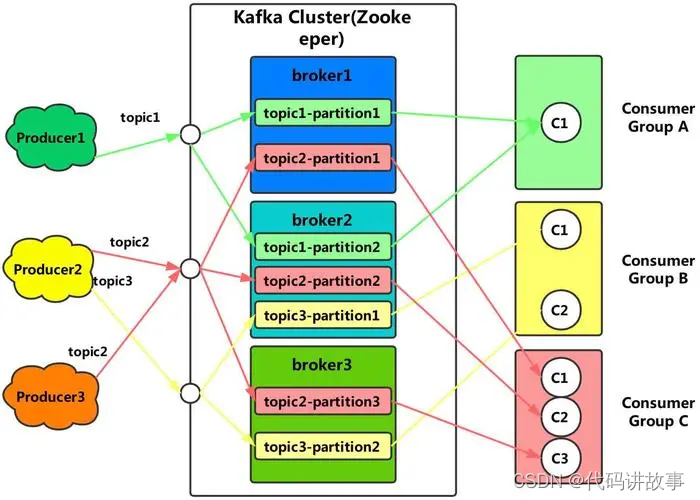
一、ACL检查流程解析
一起看一下kafka server的启动与监听流程:
Kafka -> KafkaServer -> SocketServer、KafkaRequestHandler
其中KafkaServer做相关的初始化,包括SocketServer 与 handler pool。
SocketServer的start up流程

看一下acceptor

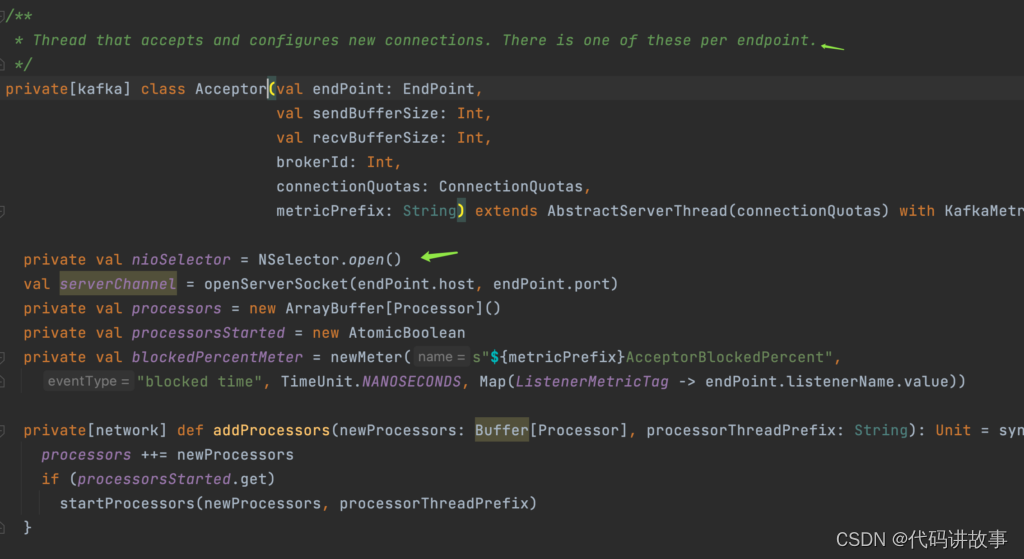
acceptor实际执行流程:监听网络事件,提交给processor处理
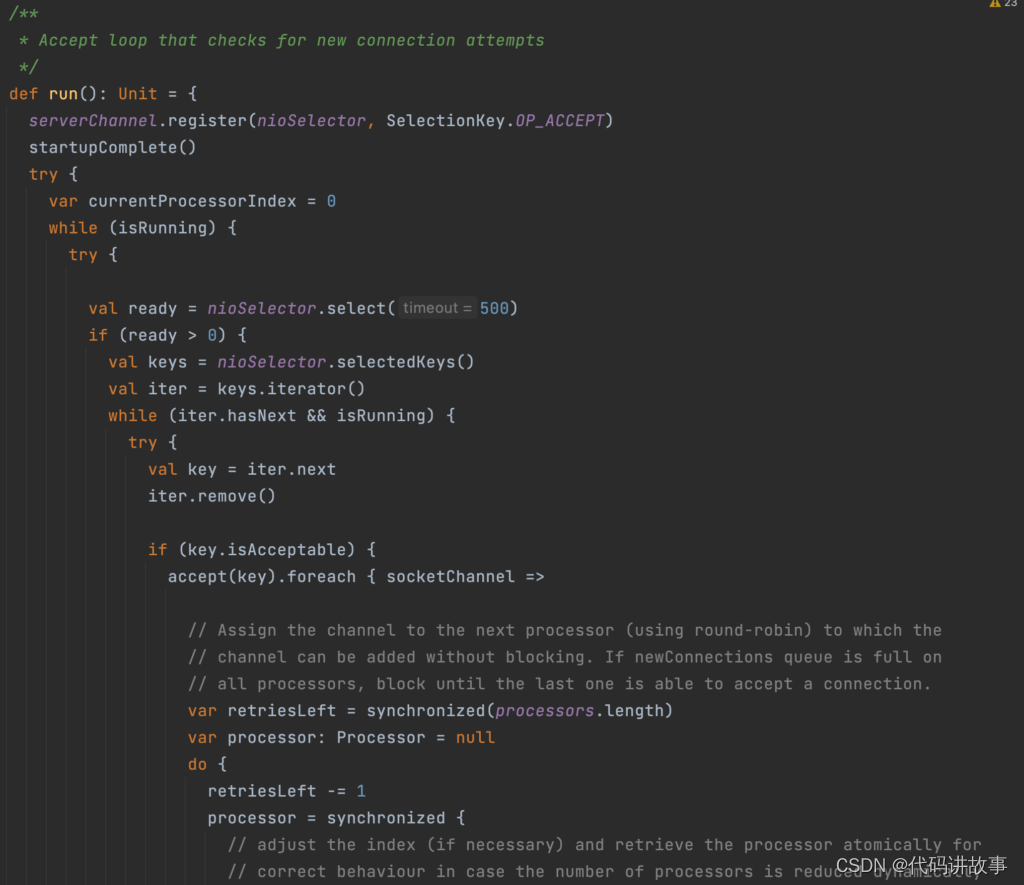
看一下processor,截取KafkaServer代码:这边的numIoThreads就是配置的具体处理线程数量。KafkaApis封装具体的各api的
相关文章:

Kafka SASL认证授权(五)ACL源码解析
Kafka SASL认证授权(五)ACL源码解析。 官网地址:https://kafka.apache.org/ 一、ACL检查流程解析 一起看一下kafka server的启动与监听流程: Kafka -> KafkaServer -> SocketServer、KafkaRequestHandler 其中KafkaServer做相关的初始化,包括SocketServer 与 han…...

logback-spring.xml 中根据不同的业务表示,分类打印到不同的文件夹、时区动态设置
logback-spring.xml 中根据不同的业务表示,分类打印到不同的文件夹、时区动态设置 logback-spring.xml 完整配置 <?xml version"1.0" encoding"UTF-8"?> <configuration debug"false" scan"true" scanPeriod&…...

linux系统编程之一
1)fcntl的使用方法 fcntl作用:可以用fcntl函数改变一个已打开的文件属性而不必重新打开文件; 堆排序是完全二叉树,但不是排序二叉树; 排序二叉树要求兄弟节点之间有大小关系,比如说左小右大; 堆排序仅要求…...

【LeetCode】《LeetCode 101》第十三章:链表
文章目录 13.1 数据结构介绍13.2 链表的基本操作206. 反转链表(简单)21. 合并两个有序链表(简单)24.两两交换链表中的节点(中等) 13.3 其它链表技巧160. 相交链表(简单)234. 回文链表…...
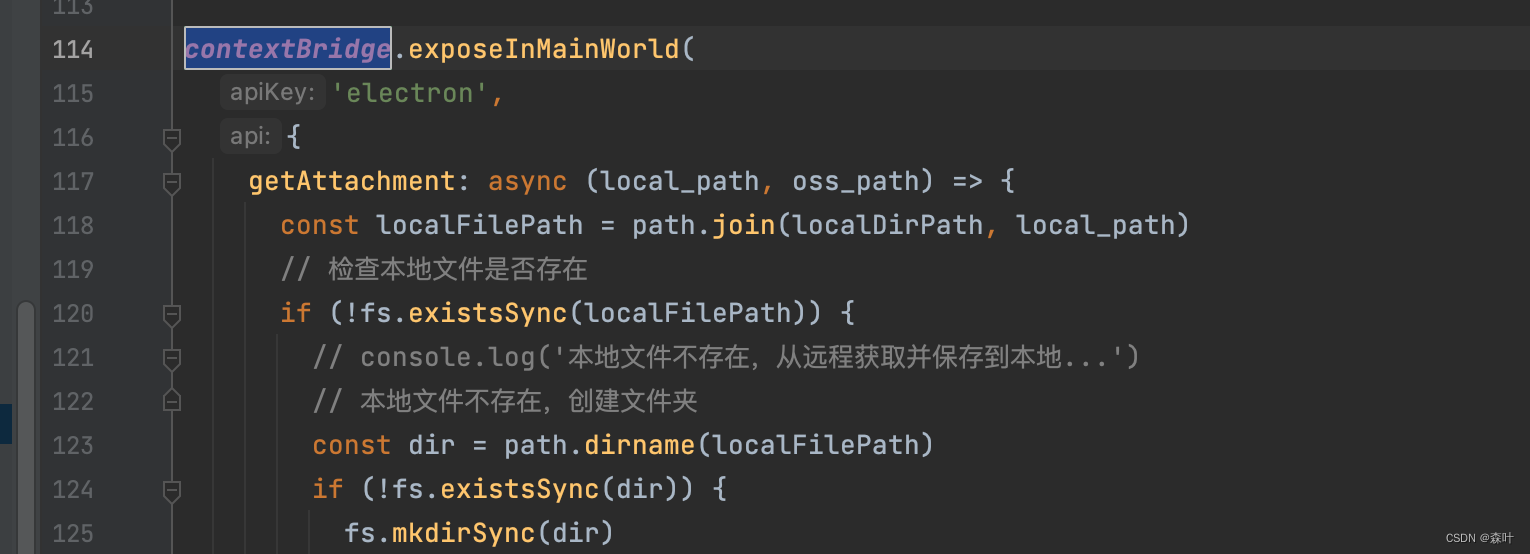
Electron webview 内网页 与 preload、 渲染进程、主进程的常规通信 以及企业级开发终极简化通信方式汇总
Electron 嵌入的页面中注入的是 preload.js 通过在标签中给 prelaod赋值,这里提到了 file://前缀,以及静态目录 static 怎么获取 实际代码,其中__static就是我们存放静态文件的地方,这个 static 是 electron 源代码根目录下的文件…...

AI人工训练师,提升外呼机器人的运营效果
外呼机器人是企业客服和营销的重要工具,外呼机器人可以通过语音识别和语音合成技术,自动拨打电话并进行客户服务和营销推广等工作。由于外呼机器人错误识别和理解偏差容易影响外呼效果,许多外呼机器人厂商选择通过AI人工训练师的技术手段来提…...
nginx正向代理、反向代理、负载均衡(重中之重)
nginx中有两种代理方式: 七层代理(http协议) 四层代理(基于tcp或udp的流量转发) 一、七层代理 原理:客户端请求代理服务器,由代理服务器转发客户端的http请求,转发到内部的服务器…...

MySQl_2
目录 函数 一.字符串函数 二.数值函数 三.日期函数 四.流程控制函数 约束 多表查询 多表关系 一.内连接 二.外连接 三.自连接 四.联合查询 五.子查询 标量子查询 列子查询 行子查询 表子查询 函数 一.字符串函数 二.数值函数 SELECT LPAD(FLOOR(RAND()*1000000),…...
)
使用Filter AND Interceptor校验等录(全网独一份,机不可失)
说明:基于spring boot进行的校验 1.熟悉如何使用jwt令牌。(不会的看这里:带你领略JWTl令牌的魅力!!!-CSDN博客) Filter和Interceptor共用文件:(可以仿照,根据…...
ubuntu20.04安装FTP服务
安装 sudo apt-get install vsftpd# 设置开机启动并启动ftp服务 systemctl enable vsftpd systemctl start vsftpd#查看其运行状态 systemctl status vsftpd #重启服务 systemctl restart vsftpdftp用户 sudo useradd -d /home/ftp/ftptest -m ftptest sudo passwd ftptest…...
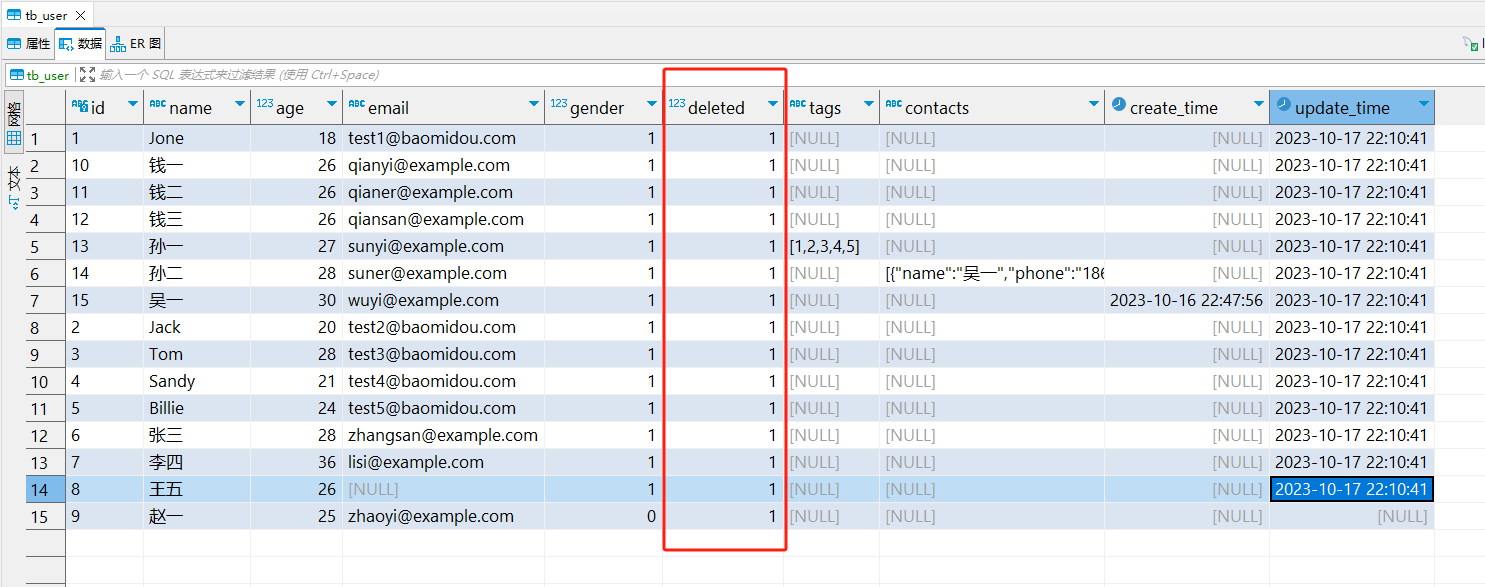
MyBatisPlus(二十)防全表更新与删除
说明 针对 update 和 delete 语句,阻止恶意的全表更新和全表删除。 实现方式 配置BlockAttackInnerInterceptor拦截器 代码 package com.example.core.config;import com.baomidou.mybatisplus.annotation.DbType; import com.baomidou.mybatisplus.extension.p…...

14.9 Socket 高效文件传输
网络上的文件传输功能也是很有必要实现一下的,网络传输文件的过程通常分为客户端和服务器端两部分。客户端可以选择上传或下载文件,将文件分块并逐块发送到服务器,或者从服务器分块地接收文件。服务器端接收来自客户端的请求,根据…...

第二节 threejs简单案例
1. 创建3D场景 // 创建3D场景对象Scene const scene new THREE.Scene();// 更改场景背景颜色 scene.background new THREE.Color(#F5F5F5);2. 创建透视投影相机 // 实例化一个透视投影相机对象 const camera new THREE.PerspectiveCamera();相机位置 // 根据需要设置相机…...
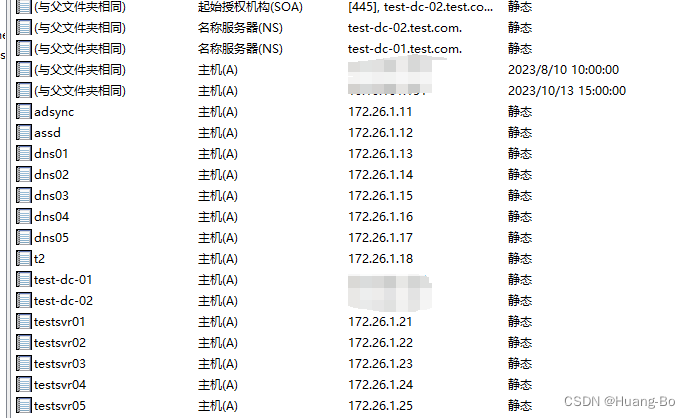
PowerShell批量修改DNS域名解析
批量添加DNS A记录 $dnsServerName"" # DNS服务器的服务器名称,如果是在DNS服务器本机执行则可留空 $containerName"test.com" # 域名的后缀也就是DNS Zone Name $mydns[WMIClass]"ROOT\MicrosoftDNS:MicrosoftDNS_resourceRecord"…...
uniapp(uncloud) 使用生态开发接口详情3(新增产品分类,产品列表,新闻列表)
我的想法是有产品分类,产品列表,新闻咨询,新闻列表 项目中, uniCloud > database 目录下新建 sy_product_nav.schema.json // 代码如下 {"bsonType": "object","required": ["classname"],"permission": {"read&…...

XTU-OJ 1339-Interprime
题目描述 n是两个连续的奇素数的平均值,且n不是素数,那么我们称这样的数是"内部素数"。求区间[a,b]内"内部素数"的个数。比如,前5个"内部素数"是4,6,9,12,15。 输入 第一行是样例数T(1≤T≤1000)。 每个样例一…...

FPGA中的LUT查找表工作原理。
在RAM中填入1110,后续的不同AB组合选通对应RAM,Y输出对应RAM存储的值,实现上面逻辑表达式的功能。...

Python爬虫:制作一个属于自己的IP代理模块
前言 在Python爬虫过程中,为了避免被网站的反爬虫机制干扰,我们需要使用IP代理。所谓IP代理,就是通过修改网络请求中的IP地址,来达到隐藏真实IP地址的效果。本文将教你如何制作一个自己的IP代理模块,让你的爬虫更加稳…...

解决QT中文乱码
选中文本带有中文字符的文件,然后按如下点击 弹出对话框,选择当前操作系统的编码格式,选择Save with Encoding 中文字符前用u8进行标识...

GPIO基本原理
名词解释 高低电平:GPIO引脚电平范围:0V~3.3V(部分引脚可容忍5V)数据0就是0V,代表低电平;数据1就是3.3V,代表高电平; STM32是32位的单片机,所以内部寄存器也都是32位的…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
