分类算法-逻辑回归与二分类
1、逻辑回归的应用场景
- 广告点击率
- 是否为垃圾邮件
- 是否患病
- 金融诈骗
- 虚假账号
看到上面的例子,我们可以发现其中的特点,那就是都属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器。
2、 逻辑回归的原理
2.1 输入
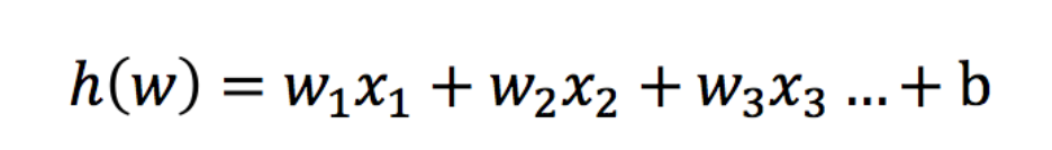
逻辑回归的输入就是一个线性回归的结果。
2.2 激活函数
- sigmoid函数
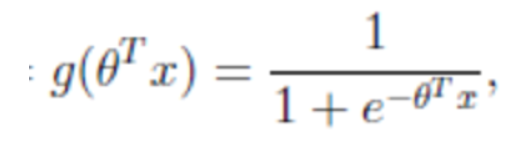
- 分析
- 回归的结果输入到sigmoid函数当中
- 输出结果:[0, 1]区间中的一个概率值,默认为0.5为阈值
逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别,并且这个类别默认标记为1(正例),另外的一个类别会标记为0(反例)。(方便损失计算)
输出结果解释(重要):假设有两个类别A,B,并且假设我们的概率值为属于A(1)这个类别的概率值。现在有一个样本的输入到逻辑回归输出结果0.6,那么这个概率值超过0.5,意味着我们训练或者预测的结果就是A(1)类别。那么反之,如果得出结果为0.3那么,训练或者预测结果就为B(0)类别。
所以接下来我们回忆之前的线性回归预测结果我们用均方误差衡量,那如果对于逻辑回归,我们预测的结果不对该怎么去衡量这个损失呢?我们来看这样一张图
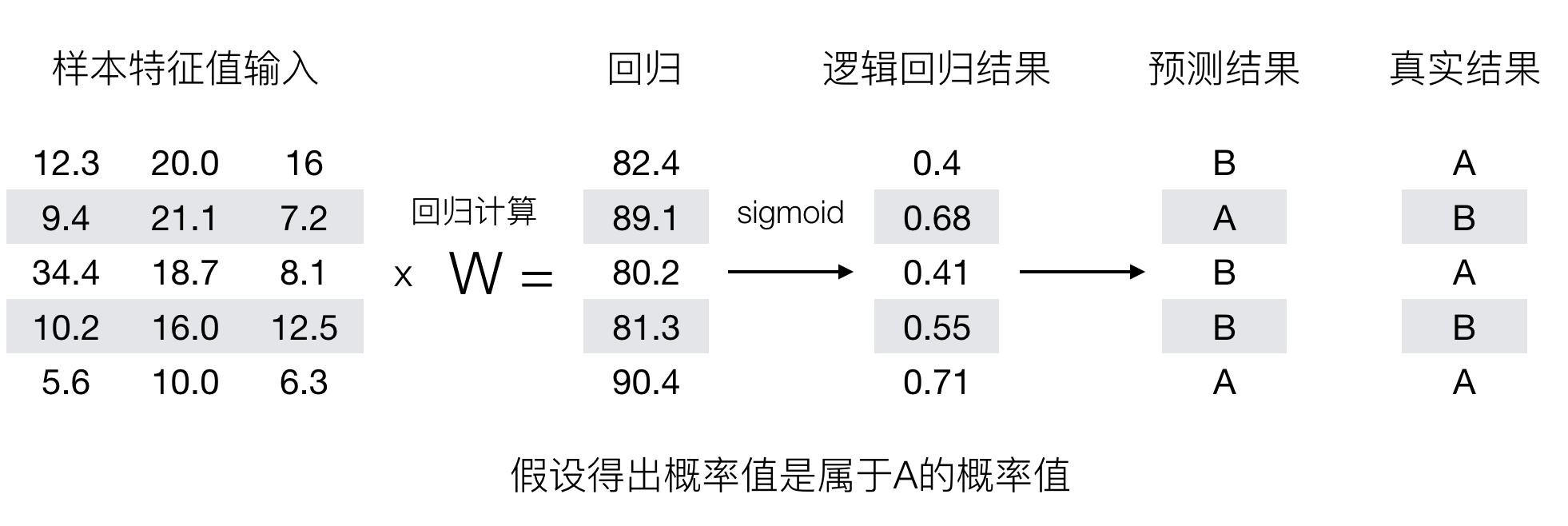
那么如何去衡量逻辑回归的预测结果与真实结果的差异呢?
2.3 损失以及优化
逻辑回归的损失,称之为对数似然损失,公式如下:
- 分段函数:
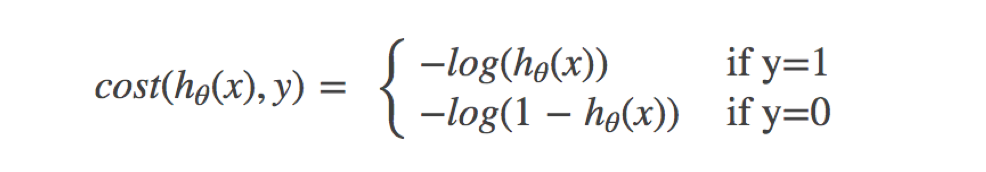
y 代表真实值,h(x)代表预测值
怎么理解单个的式子呢?这个要根据log的函数图像来理解
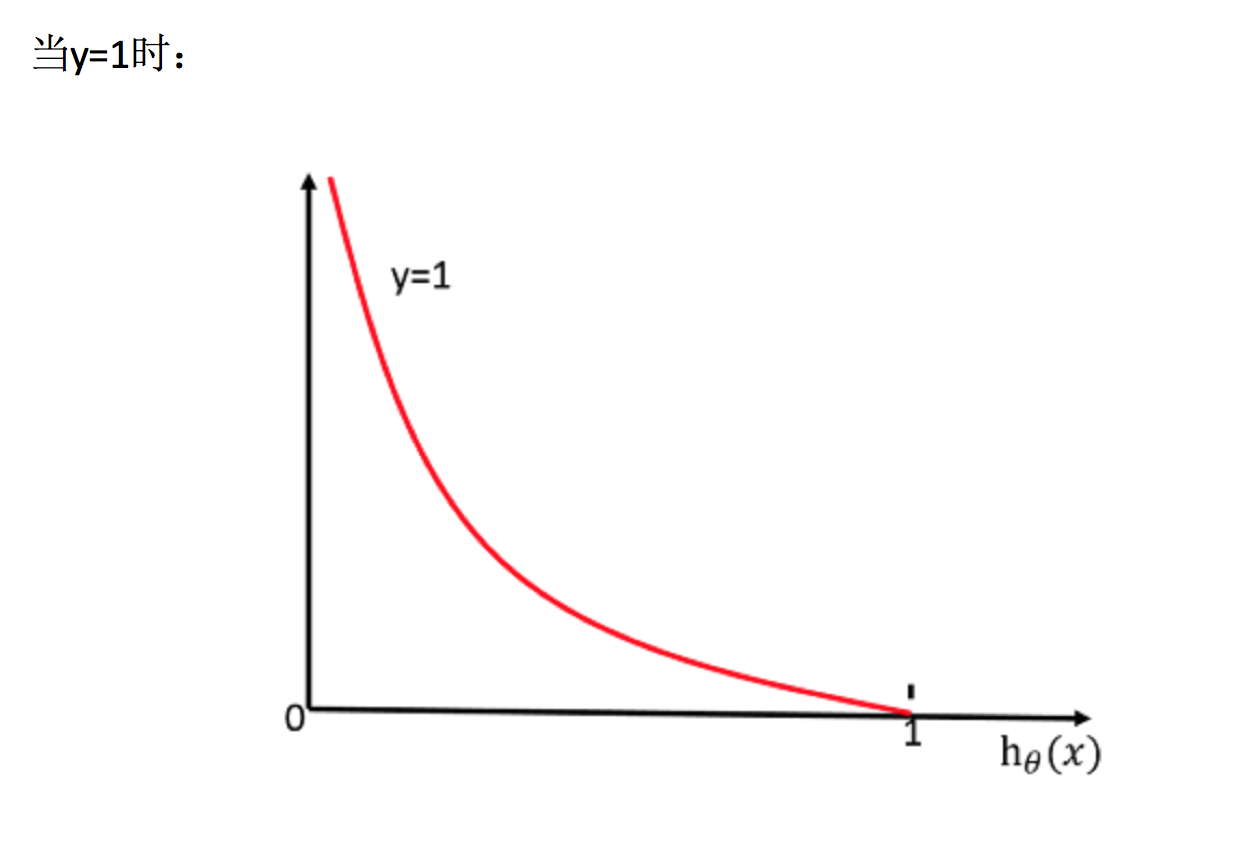
由图像可以看出,当预测值h(x)等于1的时候,纵轴(损失值)就是0,即损失值最小,符合要求;
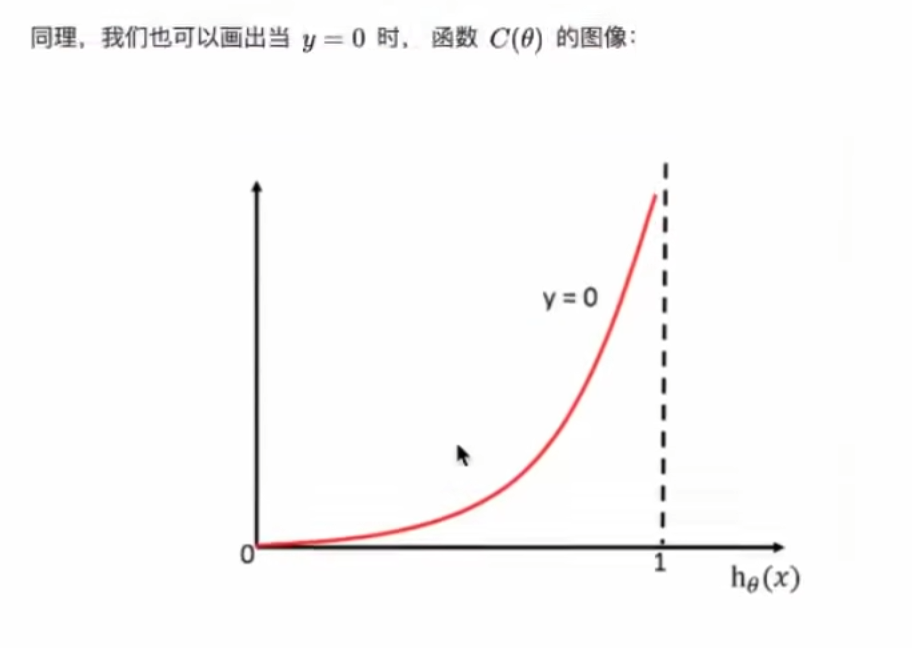
由图像可以看出,当预测值h(x)等于0的时候,纵轴(损失值)就是0,即损失值最小,符合要求;
- 综合完整损失函数
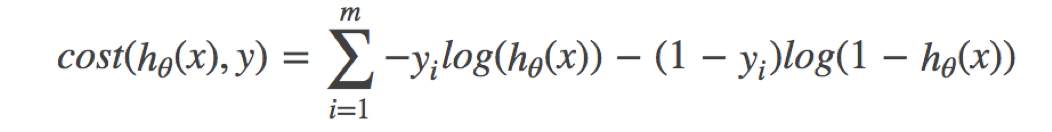
接下来我们呢就带入上面那个例子来计算一遍,就能理解意义了。

2.4 优化
同样使用梯度下降优化算法,去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数,提升原本属于1类别的概率,降低原本是0类别的概率。
3、逻辑回归API
- sklearn.linear_model.LogisticRegression(solver=‘liblinear’, penalty=‘l2’, C = 1.0)
- solver:优化求解方式(默认开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数)
- sag:根据数据集自动选择,随机平均梯度下降
- penalty:正则化的种类
- C:正则化力度
- solver:优化求解方式(默认开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数)
默认将类别数量少的当做正例
LogisticRegression方法相当于 SGDClassifier(loss=“log”, penalty=" "),SGDClassifier实现了一个普通的随机梯度下降学习,也支持平均随机梯度下降法(ASGD),可以通过设置average=True。而使用LogisticRegression(实现了SAG)
4、 案例:
通过学习时间,预测考试是否通过
5、分类的评估方法
5.1 精确率与召回率
5.1.1混淆矩阵
在分类任务下,预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合,构成混淆矩阵(适用于多分类)
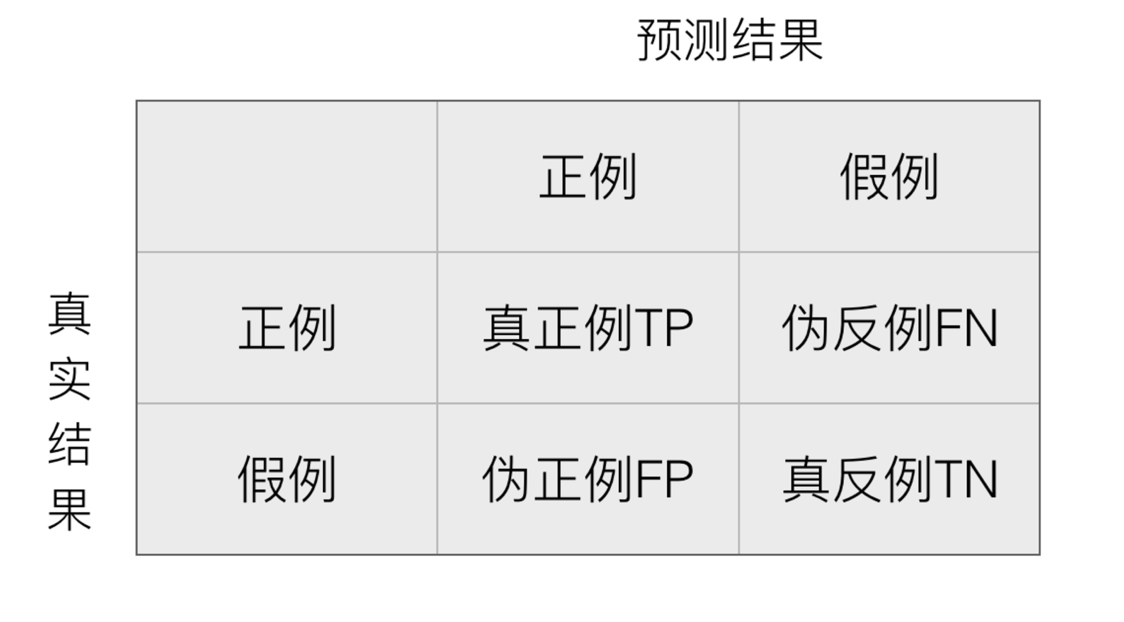
5.1.2 精确率(Precision)与召回率(Recall)
- 精确率:预测结果为正例样本中真实为正例的比例(了解)

- 召回率:真实为正例的样本中预测结果为正例的比例(查的全,对正样本的区分能力)

那么怎么更好理解这个两个概念
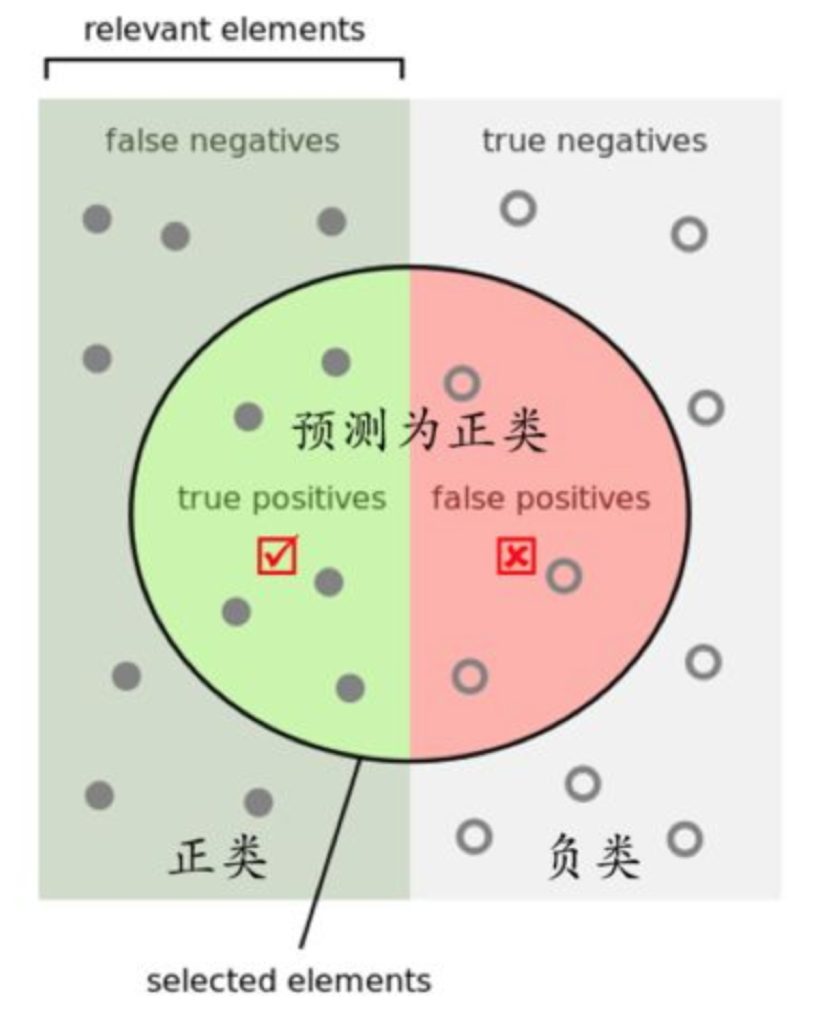
还有其他的评估标准,F1-score,反映了模型的稳健型
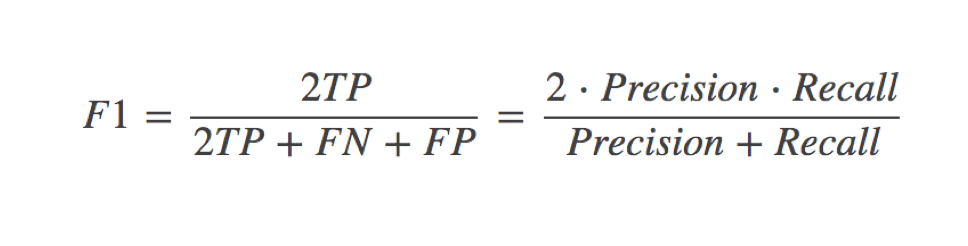
5.1.3 分类评估报告API
- sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )
- y_true:真实目标值
- y_pred:估计器预测目标值
- labels:指定类别对应的数字
- target_names:目标类别名称
- return:每个类别精确率与召回率
根据前面案例,得到结果:
print("精确率和召回率为:", classification_report(y_test, result, labels=[0, 1], target_names=['通过', '不及格']))
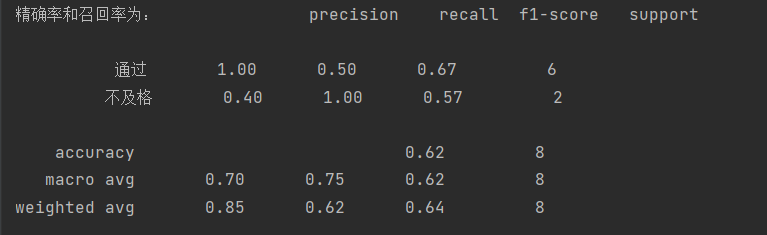
假设这样一个情况,如果99个样本癌症,1个样本非癌症,不管怎样我全都预测正例(默认癌症为正例),准确率就为99%但是这样效果并不好,这就是样本不均衡下的评估问题
问题:如何衡量样本不均衡下的评估?
5.2 ROC曲线与AUC指标
5.2.1 知道TPR与FPR
- TPR = TP / (TP + FN)
- 所有真实类别为1的样本中,预测类别为1的比例
- FPR = FP / (FP + FN)
- 所有真实类别为0的样本中,预测类别为1的比例
5.2.2 ROC曲线
- ROC曲线的横轴就是FPRate,纵轴就是TPRate,当二者相等时,表示的意义则是:对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的,此时AUC为0.5
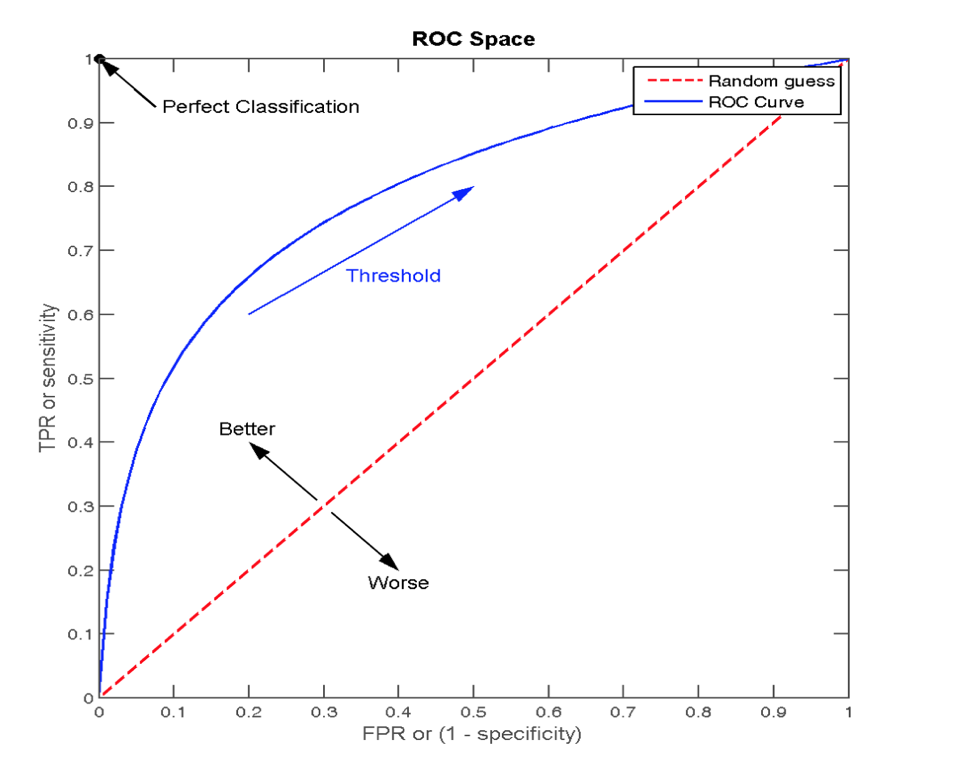
5.2.3AUC指标
- AUC的概率意义是随机取一对正负样本,正样本得分大于负样本的概率
- AUC的最小值为0.5,最大值为1,取值越高越好
- AUC=1,完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5<AUC<1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
最终AUC的范围在[0.5, 1]之间,并且越接近1越好
5.2.4 AUC计算API
- from sklearn.metrics import roc_auc_score
- sklearn.metrics.roc_auc_score(y_true, y_score)
- 计算ROC曲线面积,即AUC值
- y_true:每个样本的真实类别,必须为0(反例),1(正例)标记
- y_score:每个样本预测的概率值
- sklearn.metrics.roc_auc_score(y_true, y_score)
print("AUC指标:", roc_auc_score(y_test, model.predict(X_test)))
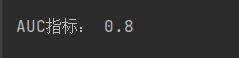
5.2.5、总结
- AUC只能用来评价二分类
- AUC非常适合评价样本不平衡中的分类器性能
相关文章:

分类算法-逻辑回归与二分类
1、逻辑回归的应用场景 广告点击率是否为垃圾邮件是否患病金融诈骗虚假账号 看到上面的例子,我们可以发现其中的特点,那就是都属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器。 2、 逻辑回归的原理 2.1 输入 逻辑回归的输入就是一个线性…...

金融液冷数据中心,噱头还是趋势?
当前,全社会数字化进程加速,金融行业已全面进入数字化和智能化时代。与此同时,随着云计算、分布式架构、大数据分析、通用人工智能等技术的广泛运用,金融行业从数据大集中到分布式融合,金融企业的数据中心建设正围绕其…...
LeetCode 高频题目分类列表
💡 LeetCode 高频面试题分类列表,总共24类,312道题目! 图 133.克隆图 207.课程表 210.课程表 II 399.除法求值 547.省份数量 684.冗余连接 743.网络延迟时间 785.判断二分图 堆 215.数组中的第K个最大元素 295.数据流的中位数 26…...

为什么模方有时候置平之后再打开,置平的地方纹理就缺失了,显示为下图中反光的灰色?
答:一般置平后结构改动多的位置会用灰面填充纹理,可以联动PS或者空三映射进行纹理贴图。 模方是一款针对实景三维模型的冗余碎片、水面残缺、道路不平、标牌破损、纹理拉伸模糊等共性问题研发的实景三维模型修复编辑软件。模方4.0新增单体化建模模块&am…...

k8s基础 随笔
写个笔记,后面再完善 部署第一个应用 为什么先实战水平扩缩?因为这个最简单,首先来部署一个喜闻乐见的nginx kubectl create deployment web --imagenginx:1.14 --dry-run -o yaml > web.yaml --dry-run表示试运行,试一下看…...
c# 关于某管理业务系统对数据统计问题.
1.业务系统主要的就是功能的稳定,流畅性. 最近客户提出某统计功能数据加载到页面很慢.反映到运维工程师处,运维跟我说之后我(研发), 我看了看代码,有几处代码确实需要优化,统计功能调用了4次服务端,每一次客户端调用服务端的时候返回结果3S左右,有三次调用服务端,一共大约耗时…...

nginx 配置相关详解
目录 Nginx的优点 Nginx简介 Nginx的优点 可以高并发连接 内存消耗少 成本低廉 配置文件非常易懂 稳定性高 内置有健康的检查功能 支持Rewrite重写 支持热部署 Nginx与Apache的对比 Nginx多进程工作原理跟设计 Nginx是如何实现高性能的 事件驱动模型 多进程机制…...

解决spring项目中无法加载resources下文件
解决spring项目中无法加载resources下文件 问题发现问题解决步骤一:检查文件名步骤二:确保测试资源目录步骤三:检查文件路径是否正确 问题发现 在学习Spring过程中,TestContext框架试图检测一个默认的XML资源位置。如果您的类被命…...
【广州华锐互动】人体血管器官3D动态展示为医学生提供哪些便利?
人体血管器官3D动态展示是一种采用先进的计算机图形技术和立体成像技术,对人体内部结构和功能进行三维可视化的教学方法。这种教学方式以其独特的优势,正在改变传统的解剖学教学模式,为医学教育带来了革新。 首先,3D动态演示能够提…...
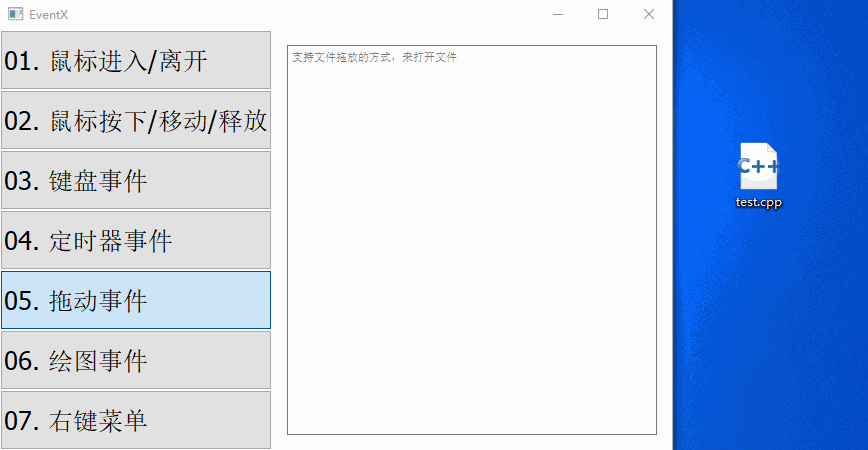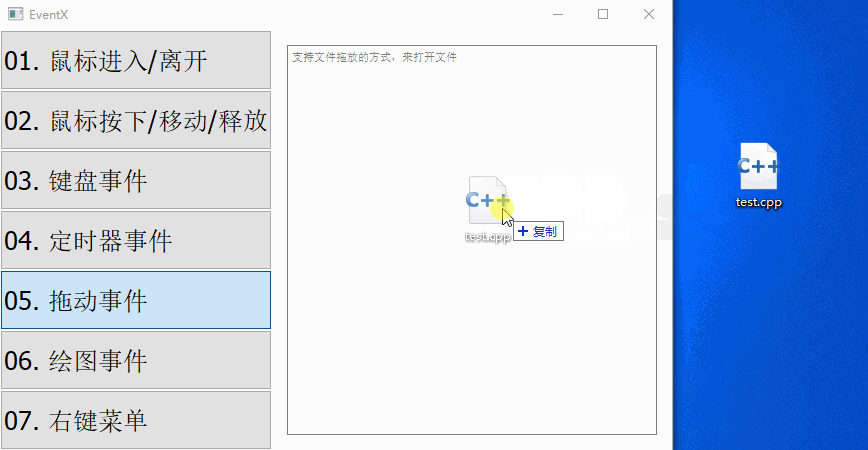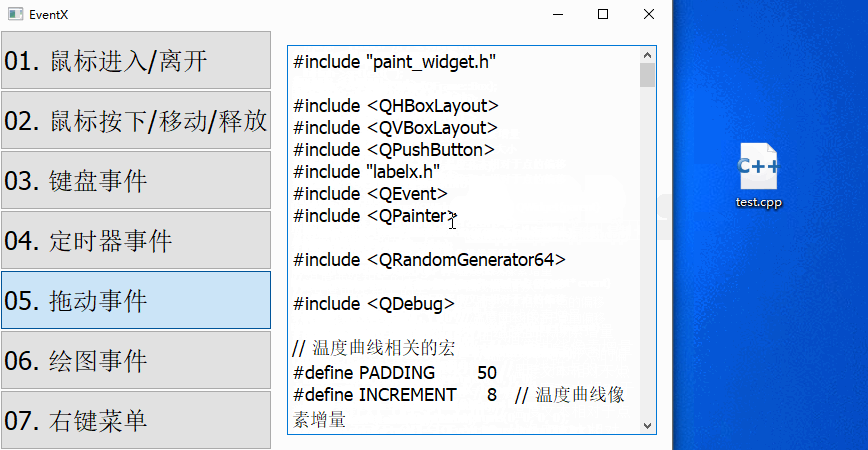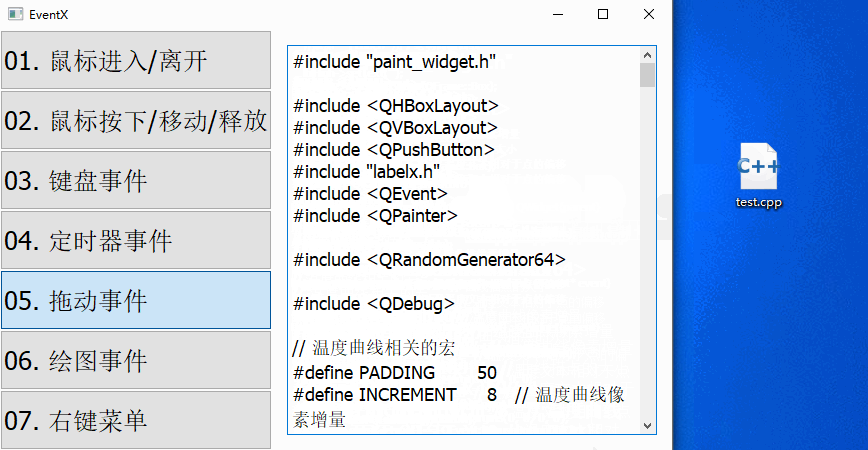
【QT开发笔记-基础篇】| 第四章 事件QEvent | 4.7 拖放事件
本节对应的视频讲解:B_站_链_接 【QT开发笔记-基础篇】 第4章 事件 4.7 拖动事件 本章要实现的整体效果如下: QEvent::DragEnter 当拖动文件进入到窗口/控件中时,触发该事件,它对应的子类是 QDragEnterEvent QEvent::DragLe…...

【Linux】介绍 Docker 的基本概念和优势,以及在应用程序开发中的实际应用
Docker 是一种轻量级的虚拟化技术,它基于 Linux 容器技术,能够在不同平台、不同主机上快速地运行和部署应用程序。Docker 的基本概念包括以下几点: 镜像(Image):Docker 镜像是一个只读的模板,它…...

GUN C/C++ undefined reference to symbol ‘dlclose@@GLIBC_2.2.5‘
编译问题: /usr/bin/ld: ../../3rdParty/lib/libluajit.a(lj_clib.o): undefined reference to symbol dlcloseGLIBC_2.2.5 //usr/lib64/libdl.so.2: error adding symbols: DSO missing from command line collect2: error: ld returned 1 exit status make[1]: …...

RabbitMQ概述,死信队列
RabbitMQ(Rabbit Message Queue)是一个开源的消息队列中间件,它实现了高级消息队列协议(AMQP)并提供可靠的消息传递机制。RabbitMQ 在分布式系统中广泛用于消息传递和事件驱动的架构。以下是一些 RabbitMQ 的重要知识点…...

【开发日常】insmod: error inserting ‘*.ko‘: -1 Unknown symbol in module原理分析
问题的起源是一次面试,面试官询问加载内核的时候,如果insmod失败,且提示Unknown symbol in module。请问我里面的原理是什么呢?为什么内核知道当前缺少的是这个symbol? 想了解下具体的原因。 首先是模拟一个环境。 写…...

圆弧插补【C#】
圆弧: 圆弧插补方法可以通过提供圆弧的起点、终点和半径来画弧。下面是一个用C#实现的圆弧插补方法的示例代码: public void DrawArc(Point startPoint, Point endPoint, int radius, bool isClockwise) {// 计算圆心坐标int centerX (startPoint.X e…...

Redis EmbeddedString
前言 Redis 写入键值对时,首先会先创建一个 RedisObject 对象来存储 Value。 如果写入的 Value 是字符串,那么 Redis 会再根据写入的字符串长度,来创建对应的 sdshdr 来存储字符串,最后把 RedisObject 的 ptr 指针指向 sdshdr。 …...

SpringMVC之WEB-INF下页面跳转@ModelAttributeIDEA tomcat控制台中文乱码问题处理
WEB-INF下页面跳转 ModelAttribute来注解非请求处理方法 用途:预加载数据,会在每个RequestMapping方法执行之前调用。 特点:无需返回视图,返回类型void IDEA tomcat控制台中文乱码问题处理 复制此段代码:-Dfile.e…...
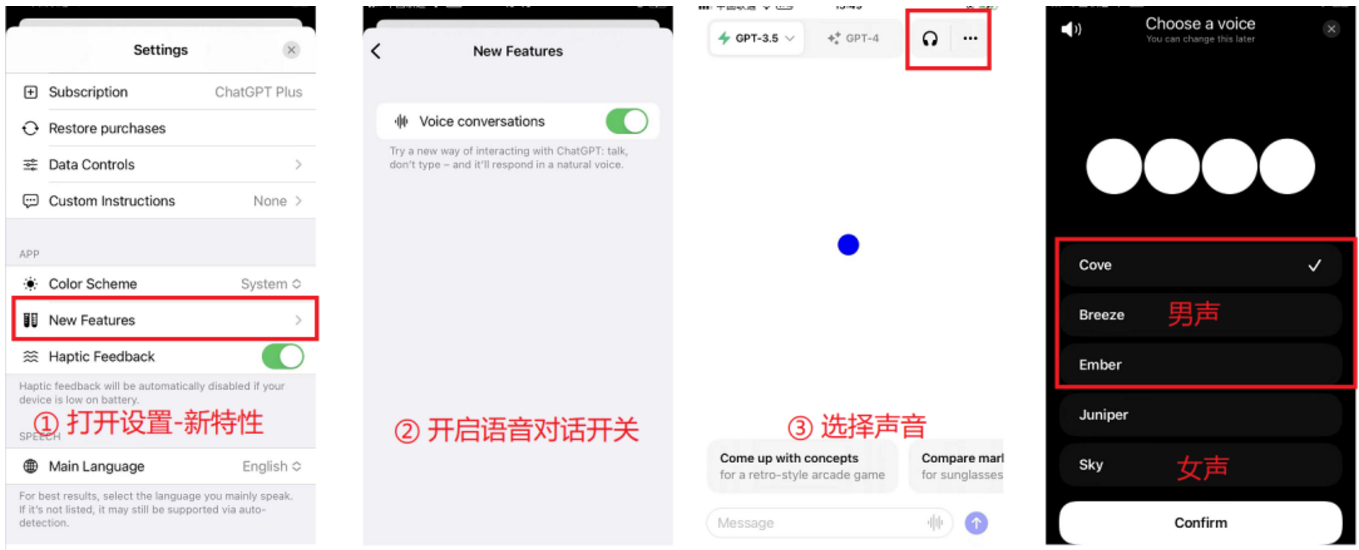
利用ChatGPT练习口语
目录 ChatGPT 这两天发布了一个激动人心的新功能,App端(包括iOS和Android)开始支持语音对话以及图片识别功能。 这两个功能一如既往的优先开放给Plus用户使用,现在将App更新到最新版本,就能体验。 为什么说激动人心&a…...
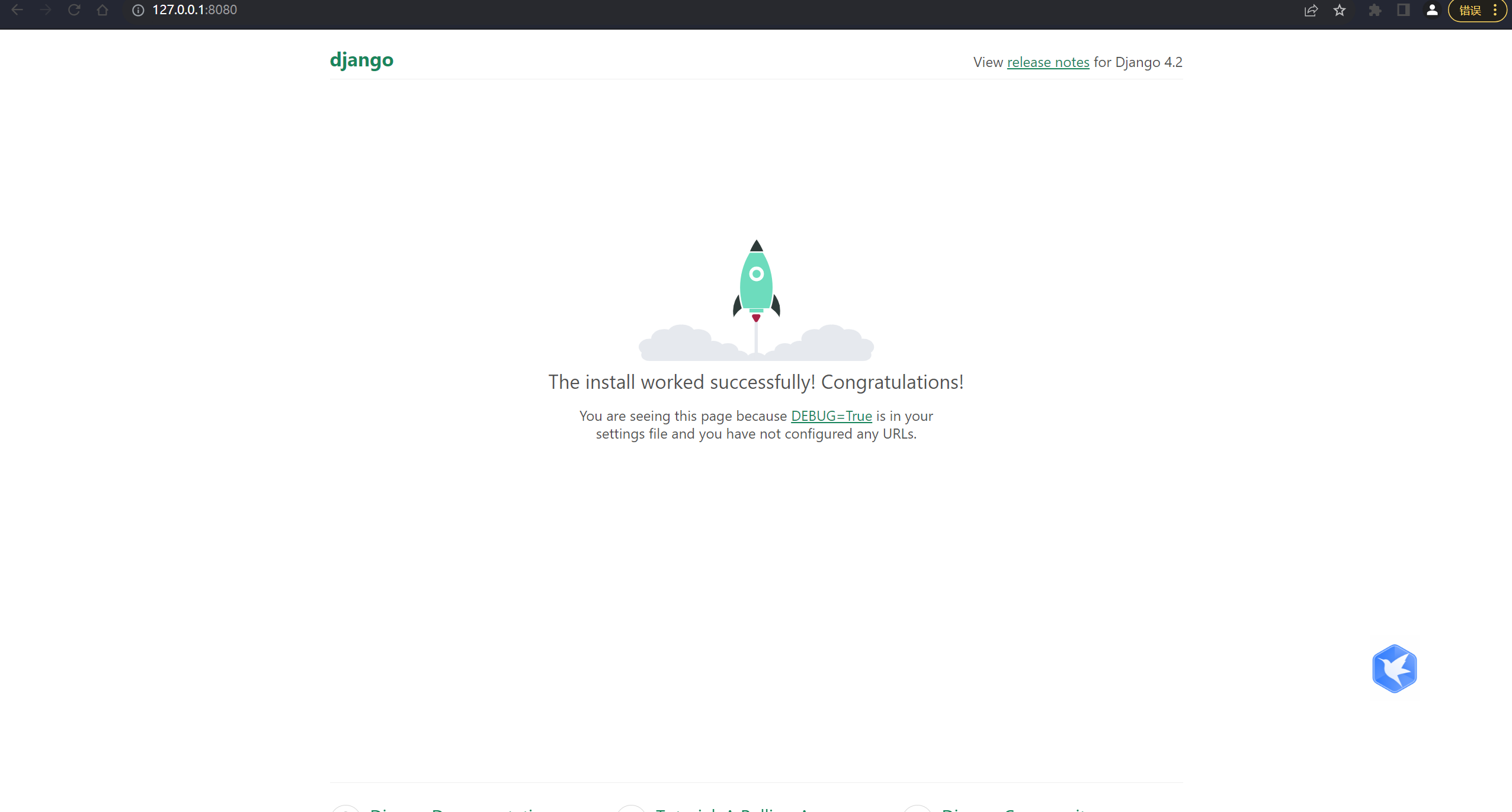
【Django 01】环境搭配与项目配置
1. 介绍 https://github.com/Joe-2002/sweettalk-django4.2#readme Django 是一个使用 Python 编写的开源 Web 应用程序框架,它提供了一套用于快速开发安全、 可扩展和高效的 Web 应用程序的工具和功能。Django 基于 MVC(Model-View-Controller…...
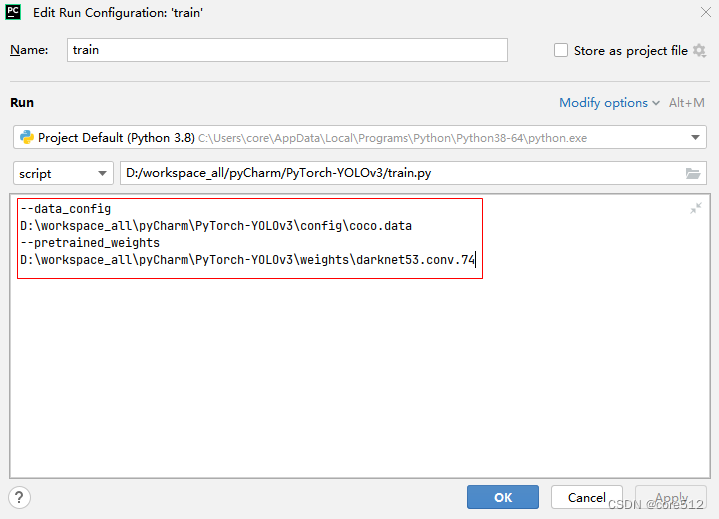
PyCharm配置运行参数
...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...
