【马蹄集】—— 概率论专题
概率论专题
目录
- MT2226 抽奖概率
- MT2227 饿饿!饭饭!
- MT2228 甜甜花的研究
- MT2229 赌石
- MT2230 square
MT2226 抽奖概率
难度:黄金 时间限制:1秒 占用内存:128M
题目描述
小码哥正在进行抽奖,箱子里有一红一白两小球,每次摸出一个球,摸到红球中奖, 如果中奖,就不再继续抽奖;如果未中奖 (摸到白球),则往箱子里补充一个白球 (摸出的白球不放回),继续抽奖,直到中奖,或者达到最大抽奖次数。
假设至多能抽奖 M M M 次,求当停止抽奖时,(中奖球数/摸出总球数) 的期望。格式
输入格式:一行,一个整数 M M M。
输出格式:保留到小数后六位。样例 1
输入:
4输出:
0.682292备注
其中: 1 ≤ M ≤ 10000 1\le M\le10000 1≤M≤10000。
相关知识点:
概率论
题解
箱子中只有一个红球和一个白球,因此第一次抽取时,抽到红球和抽到白球的概率各占一半。接下来对该箱子进行盲抽,如果抽出红色则停止抽奖;如果抽到白色则重新放入一个白球(已被抽出的白球不放回)。这就是说,对该箱子的每一次抽取,其内部总是含有一个红球和一个白球。因此这个模型实际上是一个 p = 1 2 p=\frac{1}{2} p=21 的伯努利概型。本题要求的,是停止抽奖时 “中奖球数/摸出总球数” 的数学期望。从理论上说,“抽到奖时摸出的总球数” 可以取到无穷大(即永远抽不到)。因此,本题限制假设最多能抽 M M M 次。
注意到题目要求的是 “中奖球数/摸出总球数” 的期望,而在停止抽奖时(即抽到奖或达到最大抽奖次数时),“中奖球数” 始终为1。因此我们的主要目标是算出停止抽奖时其当前 “摸出的总球数”。显然,这个值可取 1、2、……、M。具体来说,这些取值与其对应的概率如下:
- 抽 1 次中奖的概率: 1 2 \frac{1}{2} 21(第一次摸到红球),中奖球数/摸出总球数= 1 1 \frac{1}{1} 11 =1;
- 抽 2 次中奖的概率: 1 2 × 1 2 = 1 2 2 \frac{1}{2}\times\frac{1}{2}=\frac{1}{2^2} 21×21=221(第一次摸到白球,第二次摸到红球),中奖球数/摸出总球数 = 1 2 \frac{1}{2} 21 ;
- 抽 3 次中奖的概率: 1 2 2 × 1 2 = 1 2 3 \frac{1}{2^2}\times\frac{1}{2}=\frac{1}{2^3} 221×21=231(前两次摸到白球,第三次摸到红球),中奖球数/摸出总球数 = 1 3 \frac{1}{3} 31 ;
…… - 抽 M M M 次中奖的概率: 1 2 M − 1 × 1 2 = 1 2 M \frac{1}{2^{M-1}}\times\frac{1}{2}=\frac{1}{2^M} 2M−11×21=2M1(前 M − 1 M-1 M−1 次摸到白球,第三次摸到红球),中奖球数/摸出总球数 = 1 M \frac{1}{M} M1 。
我们知道,离散变量的期望公式为:
E ( X ) = ∑ x x ⋅ P ( X = x ) E\left(X\right)=\sum_xx·P(X=x) E(X)=x∑x⋅P(X=x)
其中, P ( X = x ) P\left(X=x\right) P(X=x) 表示变量取 x x x 时的概率。在本题中, x x x 的取值范围即为 1 1 \frac{1}{1} 11、 1 2 \frac{1}{2} 21、……、 1 M \frac{1}{M} M1,其对应的 P ( X = x ) = 1 2 x P\left(X=x\right)=\frac{1}{2^x} P(X=x)=2x1。因此本题所求期望的取值即为:
E ( X ) = ∑ x x ⋅ P ( X = x ) = 1 1 × 1 2 + 1 2 × 1 2 2 + ⋯ + 1 M × 1 2 M E\left(X\right)=\sum_xx·P(X=x)=\frac11×\frac12+\frac12×\frac{1}{2^2}+⋯+\frac1M×\frac{1}{2^M} E(X)=x∑x⋅P(X=x)=11×21+21×221+⋯+M1×2M1
基于此,可直接写出求解本题的完整代码:
/*MT2226 抽奖概率 离散变量的期望公式
*/
#include<bits/stdc++.h>
using namespace std;
// 求“中奖球数 / 摸出总球数” 的期望
float getException(int m){int i = 1;float ans = 0;while(i<=m){ans += 1.0/(i*pow(2,i));i++;}return ans;
}
int main()
{
// 获取输入int m; cin>>m;// 格式化输出期望 printf("%.6f",getException(m));return 0;
}
MT2227 饿饿!饭饭!
难度:黄金 时间限制:1秒 占用内存:128M
题目描述
嗯哼,小码哥在新的一年里不会忘记身为干饭人的初心!众所周知,小码哥非常不喜欢一直吃同样的东西,但由于理想与现实的差距,食堂在这 n n n 天里只会供应种 k k k 餐食。
在一天吃 3 餐的情况下,前 w w w 天一共 w × 3 w\times3 w×3 顿饭小码哥不希望有任何一顿重复。现在请问食堂有多少种方案可以满足超级可爱乖巧的小码哥的需要。格式
输入格式:一行,三个整数 n , k , w n,\ k,\ w n, k, w 表示 n n n 天内食堂只会供应 k k k 种餐食, w w w 的意义详见题面。
输出格式:输出一行一个数,表示满足小码哥需要的方案数。样例 1
输入:
5 4 1输出:
24备注
其中: 1 ≤ n , w , k ≤ 12 1\le n,\ w,\ k\le12 1≤n, w, k≤12。
相关知识点:
排列组合
题解
对题目的简化描述如下:食堂提供 n n n 种餐食,小码哥要吃 m m m 顿饭,求能使小码哥不吃重的进餐方案数。
这显然是一个排列问题。例如,当 n = 4 , m = 3 n=4,\ m=3 n=4, m=3 时,为使小码哥不吃重,其选择餐食的思路如下:
- 第一顿:小码哥可任意选择餐食,共 4 种方案;
- 第二顿:小码哥只能在剩下 3 种餐食中选择;
- 第三顿:小码哥只能在剩下 2 种餐食中选择。
于是可得到小码哥不吃重的进餐方案数为:4×3×2=24 种。
下面给出排列数的计算公式:
A n m = n × ( n − 1 ) × … × ( n − m + 1 ) = n ! ( n − m ) ! A_n^m=n\times\left(n-1\right)\times\ldots\times(n-m+1)=\frac{n!}{\left(n-m\right)!} Anm=n×(n−1)×…×(n−m+1)=(n−m)!n!
基于此,可得到求解本题的完整代码:
/*MT2227 饿饿!饭饭! 排列问题:从 k 个不同物品中选 3*w 个不同物品的方案数
*/
#include<bits/stdc++.h>
using namespace std; typedef long long ll;
// 从 n 中选取 m 个物品的排列数
ll A(ll n, ll m){ll ans = 1;for(int i=n; m>=1; i--, m--){ans *= i;}return ans;
}int main()
{// 获取输入int n,k,w; cin>>n>>k>>w;// 格式化输出总方案数cout<<A(k,3*w)<<endl; return 0;
}
MT2228 甜甜花的研究
难度:黄金 时间限制:1秒 占用内存:128M
题目描述
小码哥酷爱研究植物,他对甜甜花的研究无人能及,可他仍然在不断研究着。现在小码哥有 n n n 粒甜甜花的种子,每一粒种子都能长出不同的甜甜花,由于种子实在太多,小码哥一个人实在无法照料,于是他雇佣了 m m m 位种植能手,第 i i i 个人能照料 a i {\ a}_{i\ } ai 株甜甜花,请问小码哥有多少种分配方式将这些种子分配出去?
格式
输入格式:第一行输入以空格隔开的两个整数 N N N 和 K K K;
第二行输入 m m m 个正整数,分别代表 a i {\ a}_{i\ } ai 。输出格式:输出一个整数表示方法个数;
由于结果可能很大,须将结果对 12520 取模。样例 1
输入:
5 2
3 1输出:
20
备注
其中: n ≤ 10 4 , m ≤ 100 , a i ≤ 100 n\le{10}^4,\ m\le100,\ {\ a}_{i\ }\le100 n≤104, m≤100, ai ≤100;
数据保证种子有剩余。
相关知识点:
排列组合
题解
对题目的简化描述如下:现有 n n n 粒不同种子, m m m 个不同盒子(各盒子的容量分别为 a 1 , a 2 , … , a m a_1, a_2, … ,a_m a1,a2,…,am)。在保证种子数大于所有盒子容量之和的前提下,问有多少种不同的分装方案。
这显然是一个组合问题。例如,当 n = 8 , m = 3 ( a 1 = 1 , a 2 = 2 , a 3 = 3 ) n=8,m=3\ (a_1=1,a_2=2,a_3=3) n=8,m=3 (a1=1,a2=2,a3=3) 时,对这些种子的分装如下:
- 盒子 1:在 8 8 8 粒种子中选择 1 1 1 粒,共 C 8 1 = 8 C_8^1=8 C81=8 种方案;
- 盒子 2:在剩下 8 − 1 = 7 8-1=7 8−1=7 粒种子中选择 2 粒,共 C 7 2 = 21 C_7^2=21 C72=21 种方案;
- 盒子 3:在剩下 7 − 2 = 5 7-2=5 7−2=5 粒种子中选择 3 粒,共 C 5 3 = 10 C_5^3=10 C53=10 种方案。
因此总的分装方案数有 8×21×10=1680 种。
下面给出组合数的计算公式:
C n m = n × ( n − 1 ) × … × ( n − m + 1 ) m × ( m − 1 ) × … × 1 = n ! m ! × ( n − m ) ! C_n^m=\frac{n\times(n-1)\times\ldots\times(n-m+1)}{m\times(m-1)\times\ldots\times1}=\frac{n!}{m!\times(n-m)!} Cnm=m×(m−1)×…×1n×(n−1)×…×(n−m+1)=m!×(n−m)!n!
需要注意一点,组合数是一个关于 n n n 和 m m m 变化非常大的函数,因此实现时最好采取较大的数据范围和一定的优化方式(如一边除一边乘)。下面直接给出基于以上思路得到的完整代码:
/*MT2228 甜甜花的研究组合问题
*/
#include<bits/stdc++.h>
using namespace std; const int MOD = 12520;
const int M = 105;
int ary[M];typedef long long ll;
// 从 n 中选取 m 个物品的组合数
ll C(ll n, ll m){ll ans = 1;for(ll i=1; i<=m; i++){// 边乘边除 ans = ans*(n-m+i)/i;}return ans;
}// 对种子的分配过程
int Distribute(int n, int m){ll ans = 1;for(int i=0;i<m; i++){ans *= C(n, ary[i]);n -= ary[i];}return ans%MOD;
}int main()
{// 获取输入int n, m; cin>>n>>m;for(int i=0; i<m; i++)cin>>ary[i];// 输出期望 cout<<Distribute(n, m)<<endl;return 0;
}
MT2229 赌石
难度:黄金 时间限制:1秒 占用内存:128M
题目描述
富饶的璃月街道上有一家石料店,店主小码哥是个精明的商人,为了使他的赌石生意更加红火,他根据赌徒的心理设计了一个有趣的买卖规则:他在店铺的两边放了个小桶,一个桶里有 n n n 个红球,另一个有 n n n 个蓝球。每一批 2 n 2n 2n 个璞石与这些球一一对应,对每个来买璞石的客户,小码哥都会让他们在原地闭眼旋转数圈后走向一个小桶,若拿到蓝球则可免费获得一块石头,但若拿到红球则需要付出两倍的价钱。
假设每个人每次拿到蓝球和红球的概率相同,现在请你求出一个桶里没球而另一个桶里还剩两个球的概率,精确到小数点后四位。
格式
输入格式:输入一个正整数代表这批璞石的个数(不大于2500,且保证为偶数)。
输出格式:输出一个四位小数代表所求答案。样例 1
输入:
256输出:
0.9500
相关知识点:
排列组合
题解
对题目的简化描述如下:有两个盒子,一个盒子盛有 n n n 个蓝球,一个盒子盛有 n n n 个红球。现对这两个盒子进行随机抽取,求最终场上出现一个盒子剩 2 个球,而另一个没有球的概率。
这道题并没有说停止摸球的条件,比如当出现一个盒子没有球,而另一个盒子还剩 3、4、……、 n n n 个球时要如何算?而是直接问出现某种情况的概率。从官方给出的答案看,其对本题模型做出了以下归结:即最终只会存在 3 种情况作为结束时的状态(如下表所示)。

这也就是说,本题默认将 “一个盒子没有球,而另一个盒子还剩 3、4、……、 n n n 个球” 的情形最终归结为 “一个盒子剩 2 个球,另一个没有球” 这种情况。即认为:系统会一直摸球,直到摸到 2 n − 2 2n-2 2n−2 个球为止(当出现某个盒子已经没有球时,下一次摸球就只会从剩余有球的盒子里摸取)。下面我们基于这一设定进行分析。
题目要求的是 “一个盒子剩 2 个球,另一个没有球” 的概率,而从上面的分析可知,这类情况实际上包含了许多状态:即一个盒子没有球,而另一个盒子有2、3、4、……时都为符合要求的状态。这时,可以通过计算这些状态的出现概率(得到通项),然后再以级数的方式进行归结。这种方法有一定的难度,并且过于繁琐。在概率论里,对此类题更常用的处理方式是通过计算对立事件的概率,进而得到原事件的概率。在本题中(从两个各含 n n n 个球的盒子中随机摸 2 n − 2 2n-2 2n−2 个球),原事件 “一个盒子没有球,而另一个盒子还剩 2 个球” 的对立事件为 “两个盒子各剩下一个球”。于是接下来我们分析 “两个盒子各剩一个球的概率”。
由于摸出球的总数为 2 n − 2 2n-2 2n−2 ,如果要求最终两个盒子各剩一个球,那就要求摸出的这 2 n − 2 2n-2 2n−2 个球里,有一半的球来自指定盒子。由于题目说了每个人每次拿到蓝球和红球的概率相等,因此每一次摸球时,此球为蓝色(或红色)的概率是相等的,均为 1 2 \frac{1}{2} 21 。基于此可知:摸出 2 n − 2 2n-2 2n−2 个球里, n − 1 n-1 n−1 个球同色的概率为
p = C 2 n − 2 n − 1 ( 1 2 ) n − 1 ( 1 2 ) n − 1 = C 2 n − 2 n − 1 ( 1 2 ) 2 n − 2 p=C_{2n-2}^{n-1}\left(\frac{1}{2}\right)^{n-1}\left(\frac{1}{2}\right)^{n-1}=C_{2n-2}^{n-1}\left(\frac{1}{2}\right)^{2n-2} p=C2n−2n−1(21)n−1(21)n−1=C2n−2n−1(21)2n−2
根据该概率值,可以得到其对立事件的概率为:
1 − p = 1 − C 2 n − 2 n − 1 ( 1 2 ) 2 n − 2 1-p=1-C_{2n-2}^{n-1}\left(\frac{1}{2}\right)^{2n-2} 1−p=1−C2n−2n−1(21)2n−2
这便是本题的答案。
注意到一件事,题目给出的取值范围为 2 n ≤ 2500 2n\le2500 2n≤2500,即 n n n 最大可取到 1250,这样的范围在求组合数时必定存在过于庞大的数,这意味着即使用 long double 型也可能会越界。因此我们必须简化对该值的求解,即考虑拆分 C 2 n − 2 n − 1 ( 1 2 ) 2 n − 2 C_{2n-2}^{n-1}\left(\frac{1}{2}\right)^{2n-2} C2n−2n−1(21)2n−2 ,使得计算过程能被优化为较小的数之间的四则运算(即找到一个通项式)。
C 2 n − 2 n − 1 ( 1 2 ) 2 n − 2 = ( 2 n − 2 ) ! ( n − 1 ) ! ( n − 1 ) ! × ( 1 4 ) n − 1 = ( 2 n − 2 ) × ( 2 n − 1 ) × … × 1 ( n − 1 ) ! ( n − 1 ) ! × 1 4 n − 1 = ( 2 n − 2 ) × ( 2 n − 1 ) × … × n ( n − 1 ) ! × 1 4 n − 1 = ( 2 n − 2 ) × ( 2 n − 1 ) × … × n 4 n − 1 × [ ( n − 1 ) × ( n − 2 ) × … × 1 ] = ( n − 1 + n − 1 ) × ( n − 1 + n − 2 ) × … × ( n − 1 + 1 ) 4 ( n − 1 ) × 4 ( n − 2 ) × … × 4 ( 1 ) = ∏ i = 1 n − 1 ( n − 1 + i ) 4 i \begin{align} \nonumber &C_{2n-2}^{n-1}\left(\frac{1}{2}\right)^{2n-2} \\ \nonumber &=\frac{\left(2n-2\right)!}{(n-1)!(n-1)!}\times\left(\frac{1}{4}\right)^{n-1} \\ \nonumber &=\frac{\left(2n-2\right)\times\left(2n-1\right)\times\ldots\times1}{(n-1)!(n-1)!}\times\frac{1}{4^{n-1}} \\ \nonumber &=\frac{\left(2n-2\right)\times\left(2n-1\right)\times\ldots\times n}{(n-1)!}\times\frac{1}{4^{n-1}} \\ \nonumber &=\frac{\left(2n-2\right)\times\left(2n-1\right)\times\ldots\times n}{4^{n-1}\times\left[(n-1)\times\left(n-2\right)\times\ldots\times1\right]} \\ \nonumber &=\frac{\left(n-1+n-1\right)\times\left(n-1+n-2\right)\times\ldots\times(n-1+1)}{4(n-1)\times4\left(n-2\right)\times\ldots\times4(1)} \\ \nonumber &=\prod_{i=1}^{n-1}\frac{\left(n-1+i\right)}{4i} \end{align} C2n−2n−1(21)2n−2=(n−1)!(n−1)!(2n−2)!×(41)n−1=(n−1)!(n−1)!(2n−2)×(2n−1)×…×1×4n−11=(n−1)!(2n−2)×(2n−1)×…×n×4n−11=4n−1×[(n−1)×(n−2)×…×1](2n−2)×(2n−1)×…×n=4(n−1)×4(n−2)×…×4(1)(n−1+n−1)×(n−1+n−2)×…×(n−1+1)=i=1∏n−14i(n−1+i)
如此,就将原来求组合数的过程转换为求若干子式(小范围)的乘积。
于是得到 “一个盒子没有球,而另一个盒子还剩2个球” 的概率为:
1 − ∏ i = 1 n − 1 ( n − 1 + i ) 4 i 1-\prod_{i=1}^{n-1}\frac{\left(n-1+i\right)}{4i} 1−i=1∏n−14i(n−1+i)
下面给出基于以上思路得到的完整代码:
/*MT2229 赌石
*/
#include<bits/stdc++.h>
using namespace std; // 从两个含有 n 个球的桶中取数,最终情况为 0-2 的概率
double getProbability(int n)
{double ans = 1;for(int i=1; i<n; i++)ans *= (n-1+i)/(i*4.0);return 1-ans;
} int main()
{// 获取输入 int n; cin >> n;// 格式化输出 printf("%.4lf\n", getProbability(n/2));return 0;
}
MT2230 square
难度:钻石 时间限制:3秒 占用内存:128M
题目描述
在一个 m × n m×n m×n 的矩阵上,小码哥在左下角的顶点出现了,他只能沿着路径向上或者向右走,他的目标是 “蠕动” 到右上角的顶点,问他有多少路径可以选择。嗯,这个、这个、这个似乎地球人都知道怎么做,但是请注意,我有个条件没给呢! m m m 和 n n n 现在的最大范围是 50000,这可怎么办?仔细想想吧。
格式
输入格式:只有一行,包含两个整数 m m m 和 n n n,其均不小于 4,上限均为 50000。
输出格式:由于最后的答案数目过大,所以只检查后 100 位,输出时每行十个数字,没空格间隔,共十行,如果答案位数没超过 100 位,则需要在空位上补 0。样例 1
输入:
7 4输出:
0000000000
0000000000
0000000000
0000000000
0000000000
0000000000
0000000000
0000000000
0000000000
0000000330
相关知识点:
排列组合
题解
求从矩阵左下角到右上角的行走方案数(每次只能移动一个单位)是一个经典的迷宫问题。解决这个问题最简单的办法是动态规划,因为任意非边缘(这里的边缘主要是指与初始位置相邻的两侧,如本题中就是左侧和下侧)位置的前一个位置必定是左或下,因此可以很轻松地得到状态转移方程为:
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i ] [ j − 1 ] dp[i][j]=dp[i-1][j]+dp[i][j-1] dp[i][j]=dp[i−1][j]+dp[i][j−1]
由于这种行走方式随矩阵规格变化非常剧烈,因此大多数题目都要求记录一个对指定数的模,而本题则要求记录所有行走方式总量的末尾指定长度数串。在这样的要求下,递推求解的思路变得不再适用。
对于走格子矩阵问题(假设其规格为 m × n m\times n m×n ,表示横向有 m m m 条路径,纵向有 n n n 条路径),首先要肯定一点:从左下角走到右上角(每次移动一个单位且不可倒退),其一定会走 m + n m+n m+n 步,其中 m m m 步向右 n n n 步向上。而各移动方案之间的差异无非就是 “向上” 和 “向右” 的次序不同。例如,对于一个 2 × 3 2\times3 2×3 的矩阵,其行走方案根据 “向上” 和 “向右” 次序的不同,可分为以下 10 种不同的行走方案:
→ → ↑ ↑ ↑ → ↑ → ↑ ↑ → ↑ ↑ → ↑ → ↑ ↑ ↑ → ↑ → → ↑ ↑ ↑ → ↑ → ↑ ↑ → ↑ ↑ → ↑ ↑ → → ↑ ↑ ↑ → ↑ → ↑ ↑ ↑ → → →→↑↑↑ \\ →↑→↑↑ \\ →↑↑→↑ \\ →↑↑↑→ \\ ↑→→↑↑ \\ ↑→↑→↑ \\ ↑→↑↑→ \\ ↑↑→→↑ \\ ↑↑→↑→ \\ ↑↑↑→→ \\ →→↑↑↑→↑→↑↑→↑↑→↑→↑↑↑→↑→→↑↑↑→↑→↑↑→↑↑→↑↑→→↑↑↑→↑→↑↑↑→→
因此,走格子矩阵问题也能通过求组合数得到,此时其含义即为 “在 m + n m+n m+n 步中,选 n n n 步向上走”(或 “在 m + n m+n m+n 步中,选 m m m 步向右走”)的总方案数。即 C m + n n C_{m+n}^n Cm+nn (或 C m + n m C_{m+n}^m Cm+nm)。另一方面,本题中的 m m m 和 n n n 最大可取到 5000,这对组合数而言,是一个十分庞大的数据(任何数据类型都无法存储下),就算采取 “边乘边除” 的策略也没有一个数据类型能对中间结果进行存储,因此我们现在的问题是如何实现大范围的组合数求解?
在前面质数章节曾提到,任意一个大于 1 的正整数 n u m num num 都可以分解为若干质因数的乘幂之积:
n u m = p 1 α 1 × p 2 α 2 × … × p k α k num=p_1^{\alpha_1}\times p_2^{\alpha_2}\times\ldots\times p_k^{\alpha_k} num=p1α1×p2α2×…×pkαk
基于此,我们可将求组合数的过程进行转换:每对一个数进行乘法运算时,不直接算出乘积,而是记录当前乘数可被划分为哪些质因数之积,并对这些质因数进行相应记录。显然,对组合数分子部分的阶乘要累加记录各乘数的质因数,对组合数分母部分的阶乘要累减记录各乘数的质因数。例如,求组合数 C 20 5 C_{20}^5 C205 的过程如下(设质因数数组为 factor[ ]={0}):
C 20 5 = 20 × 19 × 18 × 17 × 16 5 × 4 × 3 × 2 × 1 C_{20}^5=\frac{20\times19\times18\times17\times16}{5\times4\times3\times2\times1} C205=5×4×3×2×120×19×18×17×16
阶段一:统计分子部分的阶乘。
- 分解 20 = 2 2 × 5 1 20=2^2\times5^1 20=22×51 ,于是有:factor[2]={2},factor[5]={1};
- 分解 19 = 19 1 19={19}^1 19=191,于是有:factor[19]={1};
- 分解 18 = 2 1 × 3 2 18=2^1\times3^2 18=21×32,于是有:factor[2]={3},factor[3]={2};
- 分解 17 = 17 1 17={17}^1 17=171,于是有:factor[17]={1};
- 分解 16 = 2 4 16=2^4 16=24,于是有:factor[2]={7}。
阶段二:统计分母部分的阶乘。
- 分解 5 = 5 1 5=5^1 5=51 ,于是有:factor[5]={0};
- 分解 4 = 2 2 4=2^2 4=22 ,于是有:factor[2]={5};
- 分解 3 = 3 1 3=3^1 3=31 ,于是有:factor[3]={1};
- 分解 2 = 2 1 2=2^1 2=21 ,于是有:factor[2]={4}。
两个阶段结束后,最终得到的质因子数组内容为:factor[3]={1}、factor[5]={1}、factor[17]={1}、factor[19]={1}。将这些质因数按其对应次数进行叠乘,即得到 C 20 4 C_{20}^4 C204 的值: 2 4 × 3 1 × 17 1 × 19 1 = 15504 2^4\times3^1\times{17}^1\times{19}^1=15504 24×31×171×191=15504 。
采取这样的方式,可将组合数在计算过程中涉及到的阶乘运算巧妙地转换为若干个质因数的乘积过程,从而避免了组合数在大数情况下容易越界的风险。另一方面,如果直接采取大数运算的方式求组合数,会出现大数除法的情况,采取质因数分解的办法可避免出现除法。
由于前面已经给出了 质因数分解 以及 大数乘法 的相关实现,在此就直接给出基于以上思路得到的求解本题目的完整代码:
/*MT2230 squre求组合数 、质因数分解、大数乘法
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 7;
const int M = 100;
// 质因数数组
int factor[N];
// 大数乘法的结果数组
int ans[M+5];
// 大数乘法(单精度*高精度)
void multi(int x)
{// 将原数组中的各数与指定数相乘for(int i=1; i<=M; i++)ans[i] *= x;// 进位处理 for(int i = 1; i <= M; i++) {ans[i + 1] += ans[i] / 10;ans[i] %= 10;}
}
int main()
{int m, n, x;cin>>m>>n;// 尽可能减少计算量 if(m>n) swap(m, n);// 记录 C(m, n) 分子 n*(n-1)*…*(n-m+1) 的质因数 for(int i=0; i<m; i++) {x= m+n-i;for(int j = 2; j<=x/j; j++) {while(x%j == 0) {x /= j;factor[j]++;}}if(x != 1)factor[x]++;}// 记录 C(m, n) 分母 m! 的质因数(约去) for(int i=1; i<=m; i++) {x = i;for(int j = 2; j<=x/j; j++) {while(x%j == 0) {x /= j;factor[j]--;}}if(x != 1)factor[x]--;}// 遍历保存的质因数,通过大数乘法统计结果 ans[1] = 1;for(int i=1; i < N; i++) {while(factor[i]) {multi(i);factor[i]--;}}// 格式化输出 for(int i=M; i>=1; i--) {cout<<ans[i];if(i%10 == 1) cout<<endl;}return 0;
}
END
相关文章:

【马蹄集】—— 概率论专题
概率论专题 目录 MT2226 抽奖概率MT2227 饿饿!饭饭!MT2228 甜甜花的研究MT2229 赌石MT2230 square MT2226 抽奖概率 难度:黄金 时间限制:1秒 占用内存:128M 题目描述 小码哥正在进行抽奖,箱子里有…...

Spring 6整合单元测试JUnit4和JUnit5
单元测试:JUnit 在之前的测试方法中,几乎都能看到以下的两行代码: ApplicationContext context new ClassPathXmlApplicationContext("xxx.xml"); Xxxx xxx context.getBean(Xxxx.class);这两行代码的作用是创建Spring容器&…...
【好书推荐】深入理解现代JavaScript
作者介绍 T. J. Crowder是一位拥有30年经验的软件工程师。在他的整个职业生涯中,他至少有一半时间是在使用JavaScript从事开发工作。他经营着软件承包和产品公司Farsight Software。他经常在Stack Overflow上为人们提供帮助,他是十大贡献者之一和JavaScr…...

高效协同: 打造分布式系统的三种模式
在构建分布式系统时,分布式协调是否总是必要选项?本文通过一些实际的例子讨论了这一问题,并通过把问题区分为是否具有单调性做为是否需要分布式协调的标准。原文: Avoiding Coordination Cost: Three Patterns for Building Efficient Distri…...

机器学习-无监督学习之聚类
文章目录 K均值聚类密度聚类(DBSCAN)层次聚类AGNES 算法DIANA算法 高斯混合模型聚类聚类效果的衡量指标小结 K均值聚类 步骤: Step1:随机选取样本作为初始均值向量。 Step2:计算样本点到各均值向量的距离,…...

智能垃圾桶丨悦享便捷生活
垃圾桶是人们日常生活所必不可少的必需品,它让生活中所产生的垃圾有了一个正确的存放地方。随着生产技术的迅速发展,垃圾桶也得以更新换代。由最初的简单式的圆筒式垃圾桶,到现在出现的感应式垃圾桶、智能语音控制垃圾桶,垃圾桶也…...

【数据结构】线性表(一)线性表的定义及其基本操作(顺序表插入、删除、查找、修改)
目录 一、线性表 1. 线性表的定义 2. 线性表的要素 二、线性表的基本操作 三、线性表的顺序存储结构 1. 定义 2. 顺序表的操作 a. 插入操作 b. 删除操作 c. 查找操作 d. 修改操作 e. 代码实例 一、线性表 1. 线性表的定义 一个线性表是由零个或多个具有相同…...

MyBatis的自定义插件
MyBatis的自定义插件 前置知识 MyBatis 可以拦截的四大组件 Executor - 执行器StatementHandler - SQL 语句构造器ParameterHandler - 参数处理器ResultSetHandler - 结果集处理器 自定义 MyBatis 插件 /*** 打印 sql 执行的时间插件*/ Intercepts(// 指定拦截器拦截的对象…...

生物制剂\化工\化妆品等质检损耗、制造误差处理作业流程图(ODOO15/16)
生物制剂、化工、化妆品等行业,因为产品为液体,产品形态和质量容易在各个业务环节发生变化,常常导致实物和账面数据不一致,如果企业业务流程不清晰,会导致系统大量的库存差异,以及财务难以核算的问题&#…...

vbv介绍
VBV模型 VBV即Video Buffer Verifier(视频缓冲区校验器)。 本质是encoder端的一个虚拟buffer,可以将VBV当做一个容量受限的管道,有一个上限容量值和下限容量值,在经过此管道的调节之后能限制编码码率在上限容量值和下限容量值之间。VBV对标NetEq中的那几个buffer(decoder b…...

Linux CentOS 8(网卡的配置与管理)
Linux CentOS 8(网卡的配置与管理) 目录 一、项目介绍二、命令行三、配置文件四、图形画界面的网卡IP配置4.1 方法一4.2 方法二 一、项目介绍 Linux服务器的网络配置是Linux系统管理的底层建筑,没有网络配置,服务器之间就不能相互…...

python -m pip install 和 pip install 的区别解析
python -m pip install 和 pip install 的区别解析 python -m pip install 使用了 -m 参数来确保以 Python 模块的形式运行 pip,适用于确保在不同的环境中正确使用 pip,这篇文章主要介绍了python -m pip install 和 pip install 的区别,需要的朋友可以参…...

深度解读js中数组的findIndex方法
js中数组有一个findIndex方法,这个方法是一个让人感到很困惑的方法。 首先来看看MDN对这个方法的解释:Array.prototype.findIndex() - JavaScript | MDN The findIndex() method of Array instances returns the index of the first element in an arra…...
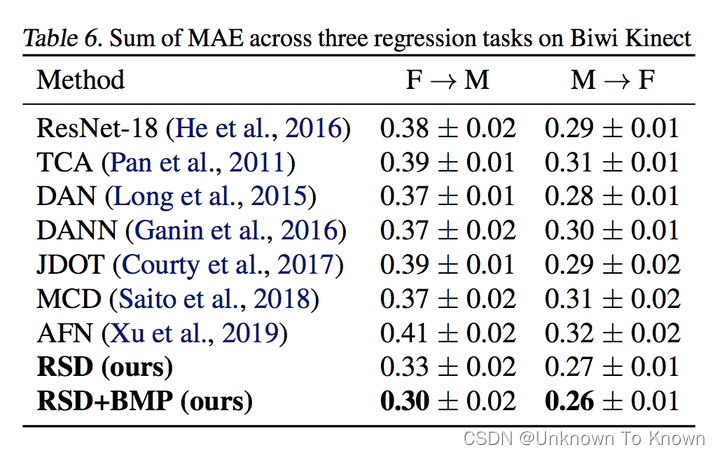
ICML2021 | RSD: 一种基于几何距离的可迁移回归表征学习方法
目录 引言动机分析主角(Principal Angle)表征子空间距离正交基错配惩罚可迁移表征学习实验数据集介绍 实验结果总结与展望 论文链接 相关代码已经开源 引言 深度学习的成功依赖大规模的标记数据,然而人工标注数据的代价巨大。域自适应&…...

中国人民大学与加拿大女王大学金融硕士:在该奋斗的岁月里,对得起每一寸光阴
在这个快速变化的世界中,金融行业面临不断更新的挑战和机遇。为了应对这些挑战,中国人民大学与加拿大女王大学合作举办金融硕士项目,旨在培养具有国际视野、扎实的金融理论基础和实战经验的专业人才。 中国人民大学和加拿大女王大学金融硕士…...

Python基础教程:装饰器的详细教程
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 一、什么是装饰器 目的:给func()方法,增加一个功能,在fun()执行期间,同时把fun()执行速率机算出来 import time def func():print(嘻嘻哈哈)start_time time.time() ti…...

Apache poi xwpf word转PDF中文显示问题解决
原问题解决方法:https://github.com/opensagres/xdocreport/issues/161 POM依赖 <properties><java.version>1.8</java.version><poi.version>3.14</poi.version></properties><dependencies><dependency><gro…...

Gartner发布2024年十大战略技术趋势
今日,Gartner发布了2024年企业机构需要探索的十大战略技术趋势。这十大趋势包括:全民化的生成式;AI 信任、风险和安全管理;AI 增强开发;智能应用;增强型互联员工队伍;持续威胁暴露管理ÿ…...

在UniApp中使用uni.makePhoneCall方法调起电话拨打功能
目录 1.在manifest.json文件中添加权限 2. 组件中如何定义 3.如何授权 4.相关知识点总结 1.在manifest.json文件中添加权限 {"permissions": {"makePhoneCall": {"desc": "用于拨打电话"}} }2. 组件中如何定义 <template>…...
苹果手机怎么刷机?掌握好这个方法!
苹果手机以其优秀的性能与高颜值的设计赢得了一大批用户的喜爱。但是,当手机使用久了以后,难免会出现一些系统问题。在遇到运行不稳定、忘记锁屏密码、软件故障、频繁死机等情况时,我们可能需要对手机进行刷机来解决问题。那么,苹…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
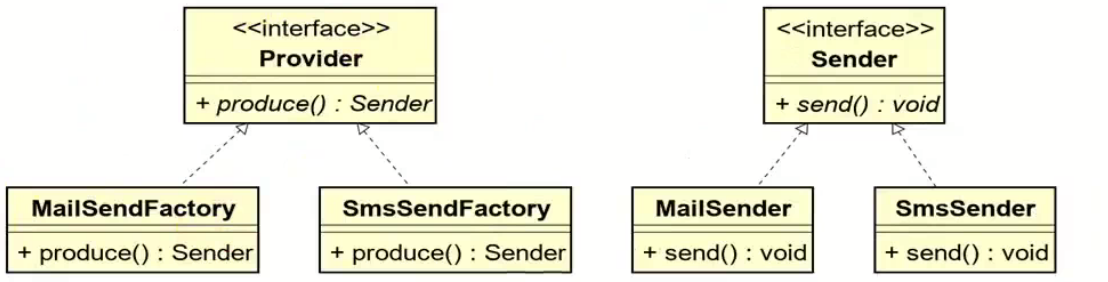
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
