损失函数总结(二):L1Loss、MSELoss
损失函数总结(二):L1Loss、MSELoss
- 1 引言
- 2 损失函数
- 2.1 L1Loss
- 2.2 MSELoss
- 3 总结
1 引言
在上一篇博文中介绍了损失函数是什么以及为什么使用损失函数,从这一篇博文就开始关于损失函数有哪些进行进一步的介绍。这里放一张损失函数的机理图:

2 损失函数
2.1 L1Loss
L1Loss(也称为MAE Loss, 平均绝对误差损失)是一种用于回归任务的损失函数。它用于度量模型的预测值与实际目标之间的绝对差距。L1Loss的数学表达式如下:
L L1 ( Y , Y ′ ) = 1 n ∑ i = 1 n ∣ y i − y i ′ ∣ L_{\text{L1}}(Y, Y') = \frac{1}{n} \sum_{i=1}^{n} |y_i - y_i'| LL1(Y,Y′)=n1i=1∑n∣yi−yi′∣
其中:
- L L1 ( Y , Y ′ ) L_{\text{L1}}(Y, Y') LL1(Y,Y′) 是整个数据集上的L1损失。
- n n n 是样本数量。
- y i y_i yi 是第 i i i 个样本的实际目标值。
- y i ′ y_i' yi′ 是第 i i i 个样本的模型预测值。
代码实现(Pytorch):
# L1Loss实现
loss = nn.L1Loss()
# 假设为预测值
input = torch.randn(3, 5, requires_grad=True)
# 实际值
target = torch.randn(3, 5)
# 计算损失函数
output = loss(input, target)
# 反向传播
output.backward()
特点:
- 只计算预测值和真实值之间差的
绝对值,对异常值(离群点)不敏感。
L1Loss损失函数适用于回归任务,但是由于其对异常值不敏感的特点,一般情况下效果均没MSELoss 效果好。现在很少使用。。。。
2.2 MSELoss
MSELoss(Mean Squared Error Loss,均方误差损失)是一种用于回归任务的损失函数,通常用于度量模型的预测值与实际目标之间的差距的平方。MSELoss的数学表达式如下:
L MSE ( Y , Y ′ ) = 1 n ∑ i = 1 n ( y i − y i ′ ) 2 L_{\text{MSE}}(Y, Y') = \frac{1}{n} \sum_{i=1}^{n} (y_i - y_i')^2 LMSE(Y,Y′)=n1i=1∑n(yi−yi′)2
其中:
- L MSE ( Y , Y ′ ) L_{\text{MSE}}(Y, Y') LMSE(Y,Y′) 是整个数据集上的均方误差损失。
- n n n 是样本数量
- y i y_i yi 是第 i i i 个样本的实际目标值。
- y i ′ y_i' yi′ 是第 i i i 个样本的模型预测值。
代码实现(Pytorch):
loss = nn.MSELoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()
特点:
- 对于与实际值偏差
较大的点会更加敏感。
MSELoss 广泛用于各种回归任务,算是最经典且最常使用的损失函数。。。。
3 总结
到此,使用 损失函数总结(二) 已经介绍完毕了!!! 如果有什么疑问欢迎在评论区提出,对于共性问题可能会后续添加到文章介绍中。如果存在没有提及的损失函数也可以在评论区提出,后续会对其进行添加!!!!
如果觉得这篇文章对你有用,记得点赞、收藏并分享给你的小伙伴们哦😄。
相关文章:

损失函数总结(二):L1Loss、MSELoss
损失函数总结(二):L1Loss、MSELoss 1 引言2 损失函数2.1 L1Loss2.2 MSELoss 3 总结 1 引言 在上一篇博文中介绍了损失函数是什么以及为什么使用损失函数,从这一篇博文就开始关于损失函数有哪些进行进一步的介绍。这里放一张损失函…...
2530. 执行 K 次操作后的最大分数(C++))
力扣(LeetCode)2530. 执行 K 次操作后的最大分数(C++)
贪心优先队列 请看答案需求:得到最大分数。易猜到,得到最大分数的取法是每次取数组中最大的数字(贪心思路)。 问题转化为:如何快速找到数组中最大的数字,根据问题规模 k 1 0 5 k10^5 k105,维护优先队列即可 O ( k l…...

C# 快速简单反射操作
文章目录 前言新反射使用BindingFlags以公有属性使用举例运行结果 前言 我之前写过一篇博客,是关于C# 反射的,我那时候使用的C# 反射写起来还是比较麻烦,需要获取Properies,再遍历Property,再找到对应Property,再使用…...
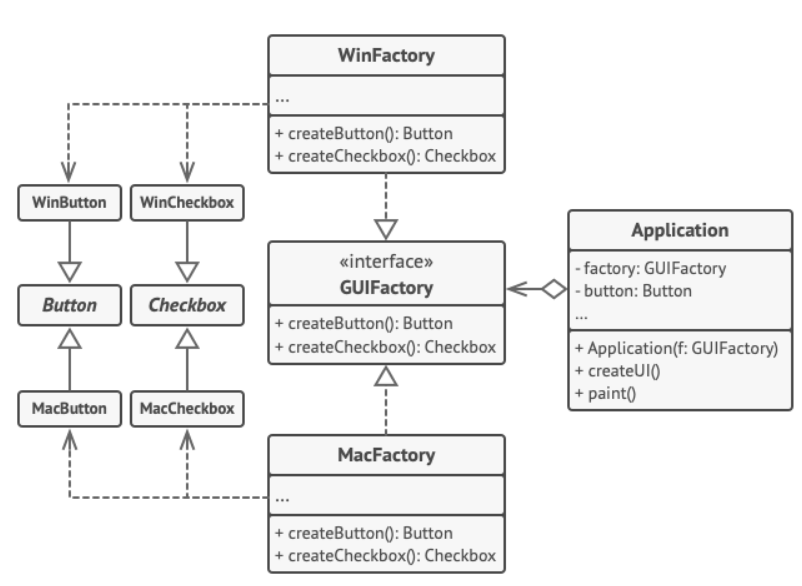
【python高级】设计模式、类工厂、对象工厂
一、说明 最近试着读Design pattern, 不过有些概念实在太抽象了, 整理一下自己所学抽象工厂的精神,就是要有abstract class(not implement),而所有不同种类的对象,都是继承这个abstract class&a…...

Flink的算子列表状态的使用
背景 算子的列表状态是平时比较常见的一种状态,本文通过官方的例子来看一下怎么使用算子列表状态 算子列表状态 算子列表状态支持应用的并行度扩缩容,如下所示: 使用方法参见官方示例,我加了几个注解: public class Bufferin…...
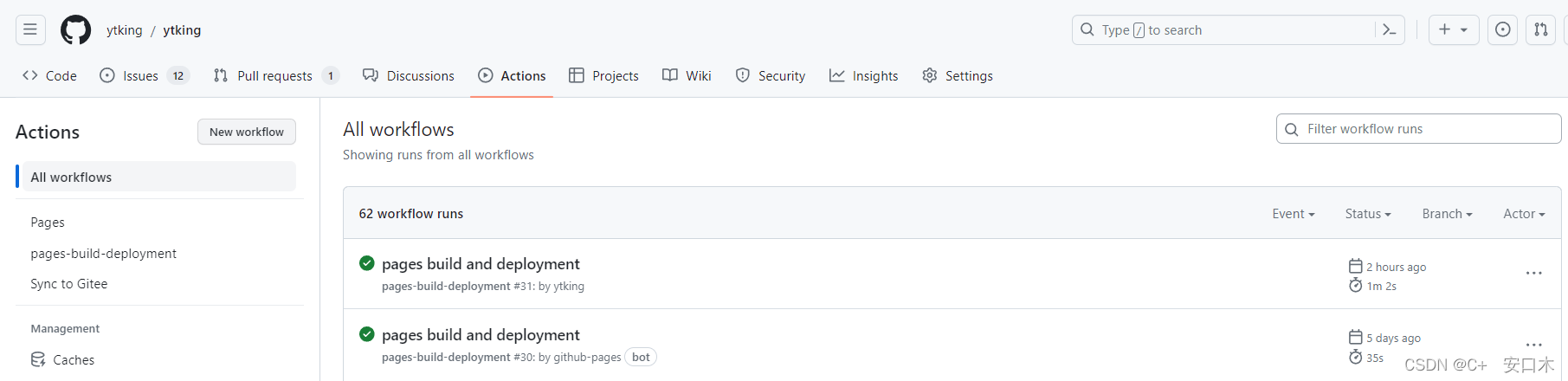
使用 Github Actions 工作流自动部署 Github Pages
GitHub-Actions actions顾名思义就是一堆动作,是一个持续集成服务,持续集成包含了拉代码、运行测试、编译代码、登录远程服务器,发布到第三方服务等等的操作,GitHub将这些操作称为actions。 概念:Workflows, Events,…...

Xposed hook 抖音账户信息
本篇主要讲下hook获取 抖音账户的相关信息,直接上代码。 public class DouHook {private static final String TAG "DouHook";public static void hook(XC_LoadPackage.LoadPackageParam lpparam) {Log.e(TAG, "DouHook start");if (lpparam …...

回顾 | E³CI效能认知与改进论坛,助力企业研发效能度量和提升
2023年8月,TiD质量竞争力大会组委会和ECI专家委员会成功举办TiD大时段课程“度量驱动研发效能提升”与“ECI效能认知与改进论坛”。与会专家以《ECI软件研发效能度量规范》团体标准为要点,为企业研发效能度量和提升分享诸多实践成果与经验。 《ECI软件研…...
)
科技的成就(五十二)
405、微信公众平台正式上线 "1995 年 8 月 24 日,微软发布 Windows 95。Windows 95 极大地改进了前续系统的图形用户界面,首次推出了开始菜单、任务栏、最大化、最小化窗口以及关闭按钮。此外,Windows 95 最大程度兼容当时的 MS-DOS 和 …...
【23种设计模式】装饰器模式
个人主页:金鳞踏雨 个人简介:大家好,我是金鳞,一个初出茅庐的Java小白 目前状况:22届普通本科毕业生,几经波折了,现在任职于一家国内大型知名日化公司,从事Java开发工作 我的博客&am…...
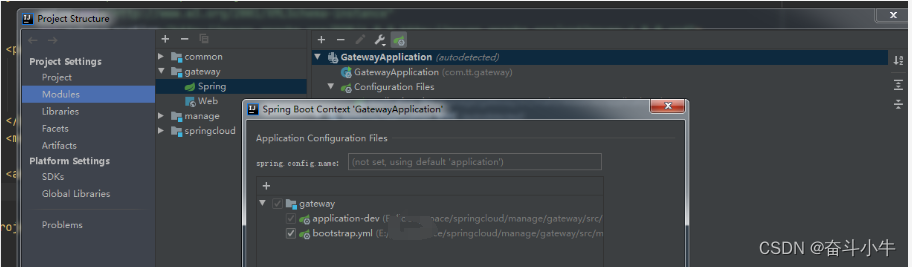
解决IDEA中SpringBoot项目创建多个子模块时配置文件小绿叶图标异常问题
在新建子模块下创建配置文件: 在子模块gateway中新建的配置文件,正常情况下配置文件左侧是小树叶标识,而这次新建application-dev.yml是个小树叶标识,bootstrap.yml是个方框。 看其他方案都是在project structure中设置,但未显示…...

【马蹄集】—— 概率论专题
概率论专题 目录 MT2226 抽奖概率MT2227 饿饿!饭饭!MT2228 甜甜花的研究MT2229 赌石MT2230 square MT2226 抽奖概率 难度:黄金 时间限制:1秒 占用内存:128M 题目描述 小码哥正在进行抽奖,箱子里有…...

Spring 6整合单元测试JUnit4和JUnit5
单元测试:JUnit 在之前的测试方法中,几乎都能看到以下的两行代码: ApplicationContext context new ClassPathXmlApplicationContext("xxx.xml"); Xxxx xxx context.getBean(Xxxx.class);这两行代码的作用是创建Spring容器&…...
【好书推荐】深入理解现代JavaScript
作者介绍 T. J. Crowder是一位拥有30年经验的软件工程师。在他的整个职业生涯中,他至少有一半时间是在使用JavaScript从事开发工作。他经营着软件承包和产品公司Farsight Software。他经常在Stack Overflow上为人们提供帮助,他是十大贡献者之一和JavaScr…...

高效协同: 打造分布式系统的三种模式
在构建分布式系统时,分布式协调是否总是必要选项?本文通过一些实际的例子讨论了这一问题,并通过把问题区分为是否具有单调性做为是否需要分布式协调的标准。原文: Avoiding Coordination Cost: Three Patterns for Building Efficient Distri…...

机器学习-无监督学习之聚类
文章目录 K均值聚类密度聚类(DBSCAN)层次聚类AGNES 算法DIANA算法 高斯混合模型聚类聚类效果的衡量指标小结 K均值聚类 步骤: Step1:随机选取样本作为初始均值向量。 Step2:计算样本点到各均值向量的距离,…...

智能垃圾桶丨悦享便捷生活
垃圾桶是人们日常生活所必不可少的必需品,它让生活中所产生的垃圾有了一个正确的存放地方。随着生产技术的迅速发展,垃圾桶也得以更新换代。由最初的简单式的圆筒式垃圾桶,到现在出现的感应式垃圾桶、智能语音控制垃圾桶,垃圾桶也…...

【数据结构】线性表(一)线性表的定义及其基本操作(顺序表插入、删除、查找、修改)
目录 一、线性表 1. 线性表的定义 2. 线性表的要素 二、线性表的基本操作 三、线性表的顺序存储结构 1. 定义 2. 顺序表的操作 a. 插入操作 b. 删除操作 c. 查找操作 d. 修改操作 e. 代码实例 一、线性表 1. 线性表的定义 一个线性表是由零个或多个具有相同…...

MyBatis的自定义插件
MyBatis的自定义插件 前置知识 MyBatis 可以拦截的四大组件 Executor - 执行器StatementHandler - SQL 语句构造器ParameterHandler - 参数处理器ResultSetHandler - 结果集处理器 自定义 MyBatis 插件 /*** 打印 sql 执行的时间插件*/ Intercepts(// 指定拦截器拦截的对象…...

生物制剂\化工\化妆品等质检损耗、制造误差处理作业流程图(ODOO15/16)
生物制剂、化工、化妆品等行业,因为产品为液体,产品形态和质量容易在各个业务环节发生变化,常常导致实物和账面数据不一致,如果企业业务流程不清晰,会导致系统大量的库存差异,以及财务难以核算的问题&#…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
