算法课作业2 OJ for Divide and Conquer
https://vjudge.net/contest/581947
A - Ultra-QuickSort
题意
每次给n个无序的数,互不重复,问最少需要多少次必要的交换操作使n个数有序。
思路
看一眼想到逆序数,然后验证了逆序数的个数符合样例,但想了一个3 2 1的话实际上只需要交换一次,但题意说的是必要交换次数也不一样是最优的交换次数,那样就太难了。
于是就简化问题求一个序列逆序数的个数,就用归并了上课讲过,可以在归并拆分返回的时候进行求逆序对,求逆序对两种,一种求每个数的右边比它小的数的个数,一种求每个数左边比它大的个数,我用第二种做的,归并返回的时候,两个数组都是有序的可以求右边的数组中每个元素,对于左边一共有几个比他大的,代码能力还行,wa了一次因为数组开的int 归并一次就写对了,我感觉我又行了哈哈哈。
#include<cstring>
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;const int maxn=500005;
long long a[maxn],box[maxn];
long long ans;
void mergesort(int left,int right)
{if(left>=right) return;int mid=(left+right)/2;mergesort(left,mid);mergesort(mid+1,right);int j=left;for(int i=mid+1;i<=right;i++){while(a[j]<a[i]&&j<=mid){j++;} ans=ans+mid-j+1;} int i=left;j=mid+1;int t=1;while(i<=mid&&j<=right){if(a[i]<=a[j])box[t++]=a[i++];elsebox[t++]=a[j++];}while(i<=mid)box[t++]=a[i++];while(j<=right)box[t++]=a[j++];t=1;for(int i=left;i<=right;i++)a[i]=box[t++];
}
int main()
{int n;while(scanf("%d",&n)&&n!=0){memset(a,0,sizeof(a));for(int i=1;i<=n;i++)scanf("%lld",&a[i]);ans=0;mergesort(1,n);
// for(int i=1;i<=n;i++)
// printf("%d ",a[i]);
// printf("\n"); printf("%lld\n",ans);} return 0;
}B - Hanoi Tower Troubles Again!
题意
给n个柱子,这个人要从第一根柱子到第n个柱子挨个往上面放球,球编号从1开始递增,要求两个相邻球编号和为完全平方数。
思路
简单模拟题
#include<cstring>
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;int box[55];
int main()
{int T;scanf("%d",&T);while(T--){int n;scanf("%d",&n);memset(box,0,sizeof(box));int i=1;while(1){int flag=0;for(int j=1; j<=n; j++){if(box[j]==0){box[j]=i++;flag=1;break;}else{int k=(int)sqrt(box[j]+i);if(k*k==(box[j]+i)){box[j]=i++;flag=1;break;}}}if(flag==0) break;}printf("%d\n",i-1);}
}
C - Fibonacci Again
思路:模拟题
#include<bits/stdc++.h>
using namespace std;const int MAXN=1000005;
int f[MAXN];
int main()
{f[0]=7;f[1]=11;for(int i=2;i<=1000000;i++) f[i]=f[i-1]%3+f[i-2]%3;int t;while(scanf("%d",&t)!=EOF){if(f[t]%3==0)printf("yes\n"); elseprintf("no\n");}return 0;
}E - Fire Net
题意
给n*n(n<=4)的格子,格子上可能有墙,或者为空地,空地可以建设碉堡,碉堡可以上下左右射击,射不穿墙,问最多可以建设多少碉堡?
思路
DFS模拟简单题
一共最多16个格子嘛,我就是从上往下,从左往右,挨个尝试每个位置,然后对于每个位置能不能安装,只需要扫描它的上方和左方是否有碉堡就可以啦,注意一下边界就好。
#include<cstring>
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;int m[10][10];
int n;
int ans;
void dfs(int start,int cnt)
{if(start>n*n){ans=max(ans,cnt);
// if(cnt>=4)
// {
// for(int i=1; i<=n; i++,printf("\n"))
// for(int j=1; j<=n; j++)
// printf("%d ",m[i][j]);
// printf("\n");
// }return;}int row=(start-1)/n+1;int col=(start-1)%n+1;for(int i=start; i<=n*n; i++){
// 取if(m[row][col]!=1){int flag=1;for(int j=col-1; j>=1&&m[row][j]!=1; j--)if(m[row][j]==2){flag=0;break;}for(int j=row-1; j>=1&&m[j][col]!=1; j--)if(m[j][col]==2){flag=0;break;}if(flag){m[row][col]=2;dfs(i+1,cnt+1);m[row][col]=0;}}
// 不取dfs(i+1,cnt);}return;
}
int main()
{while(scanf("%d",&n)&&n!=0){ans=0;getchar();for(int i=1; i<=n; i++){for(int j=1; j<=n; j++){char c;scanf("%c",&c);if(c=='.') m[i][j]=0;else m[i][j]=1;}getchar();}for(int i=1; i<=n*n; i++){dfs(i,0);}printf("%d\n",ans);}
}
/*
4
.X..
....
XX..
....
*/G - Maximum Subarray Sum
题意
最大连续子序列和
思路
简单题,注意开long long和可能超int
#include<cstring>
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int MAXN=2e5+5;
int a[MAXN];
int main()
{int n;scanf("%d",&n);for(int i=1;i<=n;i++)scanf("%d",&a[i]);long long maxx=0;long long ans=a[1];for(int i=1;i<=n;i++){maxx=maxx+a[i];ans=max(maxx,ans);if(maxx<0) maxx=0;}printf("%lld",ans);
}
J - Beat the Spread!
#include<cstring>
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>int main()
{int T;scanf("%d",&T);while(T--){int a,b;scanf("%d%d",&a,&b);if((a+b)%2){printf("impossible\n");continue;}int maxx=(a+b)/2;int minn=a-maxx;if(maxx<0||minn<0){printf("impossible\n");continue;}printf("%d %d\n",maxx,minn);}
}
相关文章:

算法课作业2 OJ for Divide and Conquer
https://vjudge.net/contest/581947 A - Ultra-QuickSort 题意 每次给n个无序的数,互不重复,问最少需要多少次必要的交换操作使n个数有序。 思路 看一眼想到逆序数,然后验证了逆序数的个数符合样例,但想了一个3 2 1的话实际上…...

申请全国400电话的步骤及注意事项
导语:随着企业的发展,越来越多的公司开始意识到全国400电话的重要性。本文将介绍申请全国400电话的步骤及注意事项,帮助企业顺利办理相关手续。 一、了解全国400电话的概念和优势 全国400电话是一种统一的客服热线号码,以“400”…...

C++ 的设计模式之 工厂方法加单例
在下面的示例中,我将演示如何创建一个工厂类,该工厂类能够生成四个不同类型的单例对象,每个单例对象都通过单独的工厂方法进行创建。 #include <iostream> #include <mutex>// Singleton base class class Singleton { protecte…...

Deploy、Service与Ingress
Deployment 自愈 介绍:控制Pod,使Pod拥有多副本,自愈,扩缩容等能力 # 清除所有Pod,比较下面两个命令有何不同效果? kubectl run mynginx --imagenginxkubectl create deployment mytomcat --imagetomcat:8.5.68 # 自…...

定制化推送+精细化运营,Mobpush助力《迷你世界》用户留存率提升23%
随着智能设备的市场下沉,手游市场迎来了爆发式增长,《迷你世界》作为一款于2015年推出的手游,一经问世就饱受欢迎。上线短短三年,迷你世界在应用商店下载量已经高达2亿次,周下载量两千万,稳居第一名&#x…...

深度学习零基础教程
代码运行软件安装: anaconda:一个管理环境的软件–>https://blog.csdn.net/scorn_/article/details/106591160(可选装) pycharm:一个深度学习运行环境–>https://blog.csdn.net/scorn_/article/details/106591160…...

简单测试一下 展锐的 UDX710 性能
最近在接触 联通5G CPE VN007 ,发现使用的是 展锐的Unisoc UDX710 CPU,正好简单的测试一下这颗CPU CPU信息 UDX710 是一颗 双核 ARM Cortex-A55 处理器,主频高达 1.35GHz processor : 0 BogoMIPS : 52.00 Features : fp…...
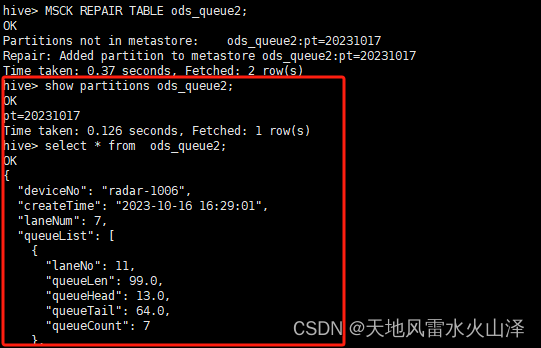
一百九十、Hive——Hive刷新分区MSCK REPAIR TABLE
一、目的 在用Flume采集Kafka中的数据直接写入Hive的ODS层静态分区表后,需要刷新表,才能导入分区和数据。原因很简单,就是Hive表缺乏分区的元数据 二、实施步骤 (一)问题——在Flume采集Kafka中的数据写入HDFS后&am…...

智慧公厕:探索未来城市环境卫生设施建设新标杆
智慧公厕是当代城市建设的一项重要举措,它集先进技术、人性化设计和智能管理于一体,为人们提供更为舒适、便捷和卫生的厕所环境。现代智慧公厕的功能异常丰富,从厕位监测到多媒体信息交互,从自动化清洁到环境调控,每一…...

高压放大器在无线电能中应用有哪些
高压放大器是一种用于放大电信号的放大器,可以将输入的低电压信号放大到更高的输出电压水平。在无线电通信和其他相关领域中,高压放大器具有广泛的应用。本文将详细介绍高压放大器在无线电能中的应用。 无线电发射:高压放大器在无线电发射中起…...

若依集成MybatisPlus
目录 一、依赖变更 1. MybatisPlus依赖 2. pagehelper依赖修改 二、相关配置 1. yml配置 1.1 注释掉原Mybatis配置 1.2 加入MybatisPlus的配置 1.3 注释掉原MybatisConfig.class 三、其他配置及功能实现 1. 自动补全create_time等信息 2. 实现MP分页 3. 实现Mybati…...
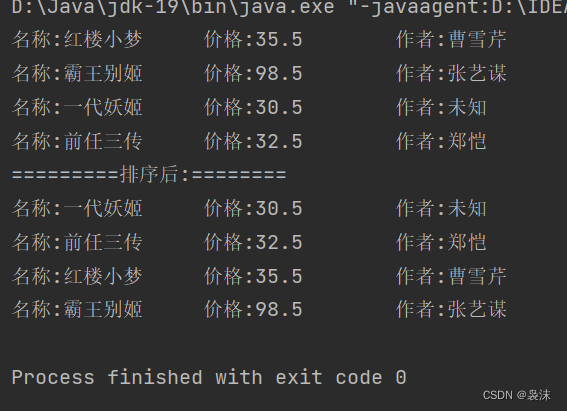
List小练习,实现添加图书,并且有序遍历
SuppressWarnings({"all"})public static void main(String[] args) {List list new LinkedList(); // List list new Vector(); // List list new ArrayList();list.add(new Book1("红楼小梦",35.5,"曹雪芹"));list.add(new B…...

代码随想录二刷 Day42
62.不同路径 简单题目自己就可以写出来,注意下创建二维vector的方法就可以, dp table如下 class Solution { public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m,vector<int>(n,0));for (int i 0; i < n; i ) {dp[…...

【Android】Drawable 和src 的区别和理解
详细讲解 在 Android 中,ImageView 的 src 属性和 background 属性用于设置不同类型的图像内容。下面是它们的详细解释: src 属性:该属性用于设置 ImageView 中显示的图像内容。它可以接受一个图像资源的引用,可以是一个图片文件…...

Linux网络-UDP/TCP协议详解
Linux网络-UDP/TCP协议详解 2023/10/17 14:32:49 Linux网络-UDP/TCP协议详解 零、前言一、UDP协议二、TCP协议 1、应答机制2、序号机制3、超时重传机制4、连接管理机制 三次握手四次挥手5、理解CLOSE_WAIT状态6、理解TIME_WAIT状态7、流量控制8、滑动窗口 丢包问题9、拥塞控制…...
C语言从入门到高级
C语言是“编程语言之首”(很多人学习的第一门编程语言),学好一门编程语言需要明确其学习路径,下面分享下我的学习路径,希望对您有所帮助。 一、C语言入门 (1)C语言概述 (2&#x…...
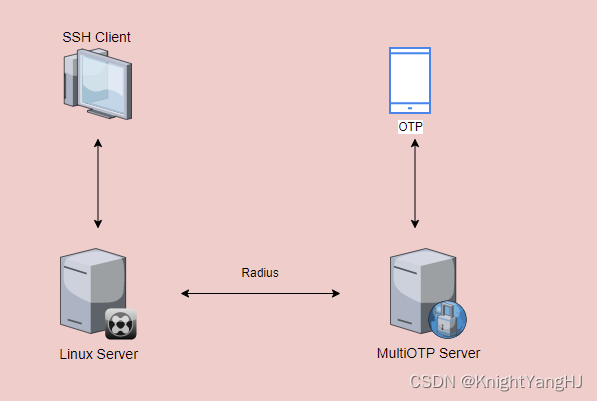
【MultiOTP】在Linux上使用MultiOTP进行SSH登录
在前面的文章中【FreeRADIUS】使用FreeRADIUS进行SSH身份验证已经了解过如何通过Radius去来实现SSH和SUDO的登录,在接下来的文章中只是将密码从【LDAP PASSWORD Googlt OTP】改成了【MultiOTP】生成的passcode,不在需要密码,只需要OTP去登录…...
性能超越 Clickhouse | 物联网场景中的毫秒级查询案例
1 物联网应用场景简介 物联网(Internet of Things,简称 IoT)是指通过各种信息传感、通信和 IT 技术来实时连接、采集、监管海量的传感设备,从而实现对现实世界的精确感知和快速响应,继而实现自动化、智能化管理。在查…...

05、SpringBoot 集成 RocketMQ
目录 SpringBoot集成RocketMQ消息发送三种方式1、同步消息producer-springboot创建项目添加依赖配置文件同步消息发送代码启动类Test类 comsumer-springboot创建项目添加依赖配置文件同步消息消费代码 2、异步消息生产者消费者 3、一次性消息生产者消费者 消息消费两种方式1、集…...
PR2023中如何导入字幕
PR中如何导入字幕 方法一: 点开文本,字幕,新建字幕分段(点击右上角…三个点) 键入调整内容 方法二 点开基本图形,编辑,调整,拖动位置。...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
