开路、断路和短路区别
文章目录
- 开路和断路
- 击穿
- 电源短路、用电器短路、对地短路和对电源短路
开路和断路
开路和断路是电路中两种用于描述电流流动情况的状态。
两者易混淆,常被混淆使用,但是它们还是有所不同。
-
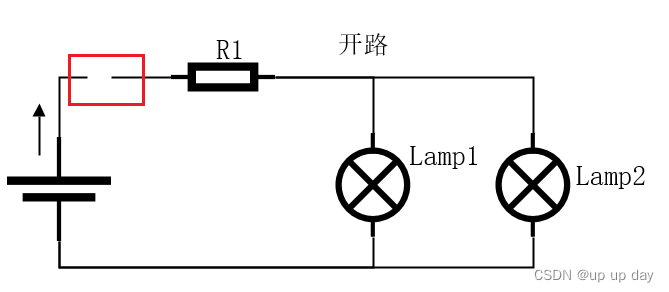
开路表示电路中存在一个断链,电流无法从一个点流到另一个点,也没有其他路径可以流动;
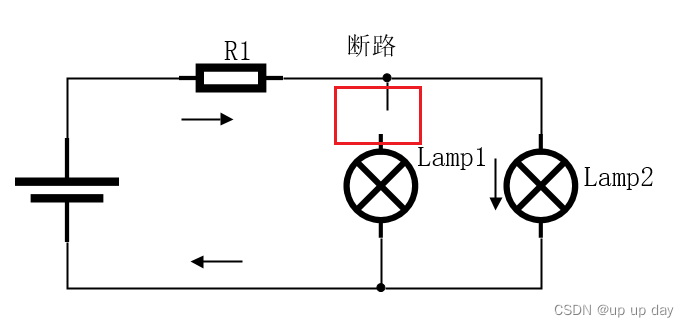
断路表示电路中存在一个完全断开的线路,因此电流无法通过此线路流动,但是电路中任然存在其他路径,电流可以通过其他路径流动。 -
对于开路,往往会导致电路中所有元件停止工作;
而断路,只影响电路中的一部分。 -
开路表示电路中不存在电流流动;
而断路表示电路中某一部分不通过电流流动,但是电路中任然存在其他路径。
击穿
击穿是指一个电子元器件由于某种原因导致的彻底损坏,击穿往往是指二极管、晶体管或者场效应晶体管,
如二极管正常情况下应该是正向导通,反向截止,但是如果一个比较高的电压到来,就会将其击穿,击穿后,无论电压是正向还是反向,它都会导通,这就是击穿现象。
电源短路、用电器短路、对地短路和对电源短路
众所周知,电流总是趋向于流向电阻小的路径。
电路中有很大电流流过,但电流不流过负载,负载不工作。由于电流很大,电源和导线很容易被烧坏。
-
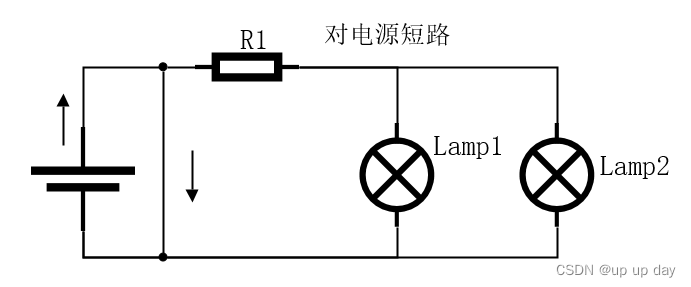
电源短路是指电流不经过任何用电器,直接由正极经过导线流回负极,容易烧坏电源;
-
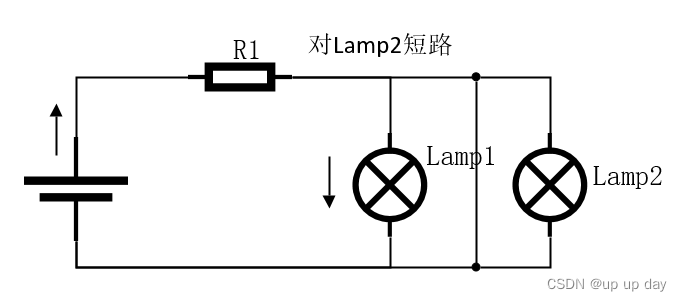
用电器短路,也叫部分电路短路,即一根导线接在用电器的两端,此用电器被短路,容易产生烧毁其他用电器的情况。
-
对电源短路是指电源电压直接短接到负载电路上,导致电流异常增大,甚至导致电源保护动作的故障现象。
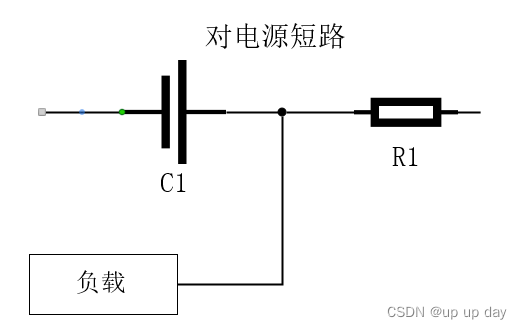
-
对地短路是指电路中某个元件短路到地线或者其他金属部件,使电路中流动的电流异常增大。
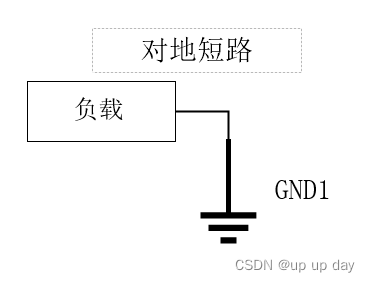
相关文章:

开路、断路和短路区别
文章目录 开路和断路击穿电源短路、用电器短路、对地短路和对电源短路 开路和断路 开路和断路是电路中两种用于描述电流流动情况的状态。 两者易混淆,常被混淆使用,但是它们还是有所不同。 开路表示电路中存在一个断链,电流无法从一个点流到…...

springBoot web开发自动配置和默认效果
web开发自动配置和默认效果 自动配置默认配置 自动配置 绑定了配置文件的一堆配置项 1、springMVC的所有配置 spring.mvc 2、Web场景通用配置 spring.web 3、文件上传配置 spring.servlet.multipart 4、服务器的配置serve: 比如:编码方式等 默认配置 重要…...
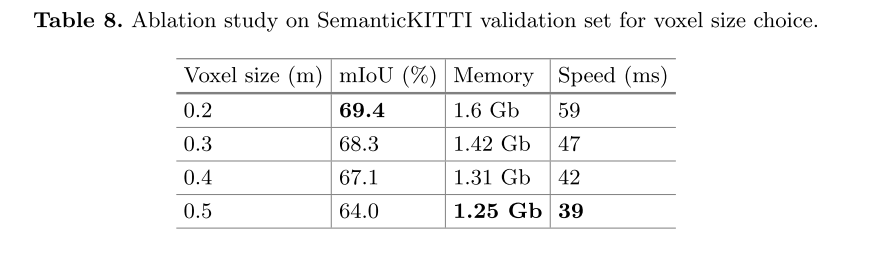
论文阅读:Efficient Point Cloud Segmentation with Geometry-Aware Sparse Networks
来源:ECCV2022 链接:Efficient Point Cloud Segmentation with Geometry-Aware Sparse Networks | SpringerLink 0、Abstract 在点云学习中,稀疏性和几何性是两个核心特性。近年来,为了提高点云语义分割的性能,人们提…...
1-k8s1.24-底座搭建-基于containerd
文章目录 一、服务器准备二、安装Containerd三、安装k8s四、安装部署dashboard ps:第一遍搭建ks8的时候,由于k8s在1.24版本之后就放弃了对docker的支持,如果要继续使用docker需要自己加载插件。所以一开始就是直接使用 k8s1.24containerd进行…...

Java文件前后端上传下载工具类
任何非压缩格式下载 package com.pisx.pd.eco.util;import java.io.*; import java.util.Collections; import java.util.HashMap; import java.util.Map;import javax.servlet.ServletOutputStream; import javax.servlet.http.HttpServletResponse;import org.springframewo…...

内燃机可变气门驱动研究进展
Review of Advancement in Variable Valve Actuation of Internal Combustion Engines AbstractIntroduction燃烧和气体交换需要电子控制 paper Abstract 近年来,人们对空气污染和能源使用的日益关注导致了车辆动力总成系统的电气化。 另一方面,一个多世…...

NEFU离散数学实验2-容斥原理
相关概念 离散数学中的容斥原理是一种使用集合运算的技巧,通常用于计算两个或更多集合的并集或交集的大小。以下是一些与容斥原理相关的常见概念和公式。 概念: 1. 集合:由元素组成的对象,通常用大写字母表示,如A、B、…...
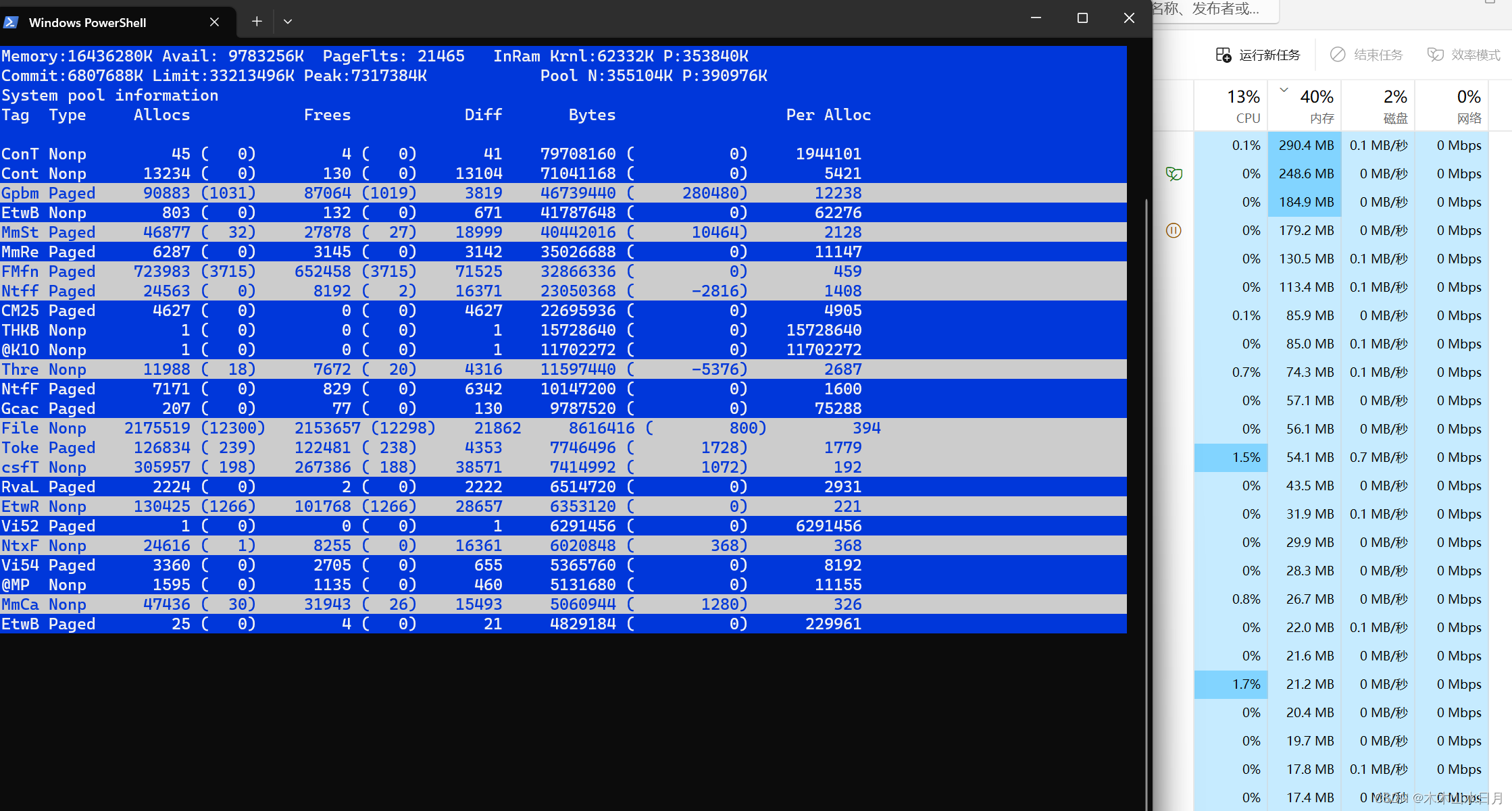
解决Windows内存溢出/占满死机问题-PoolMon工具
某一天, 工作所用笔记本突然越来越卡直至死机 以为只是windows11的抽风行为,之前就因为windows11资源管理器经常卡死(后升级小版本好多了)。 遂长按电源键强制关机重启。 然慢慢又越来越卡,直至卡死,无…...
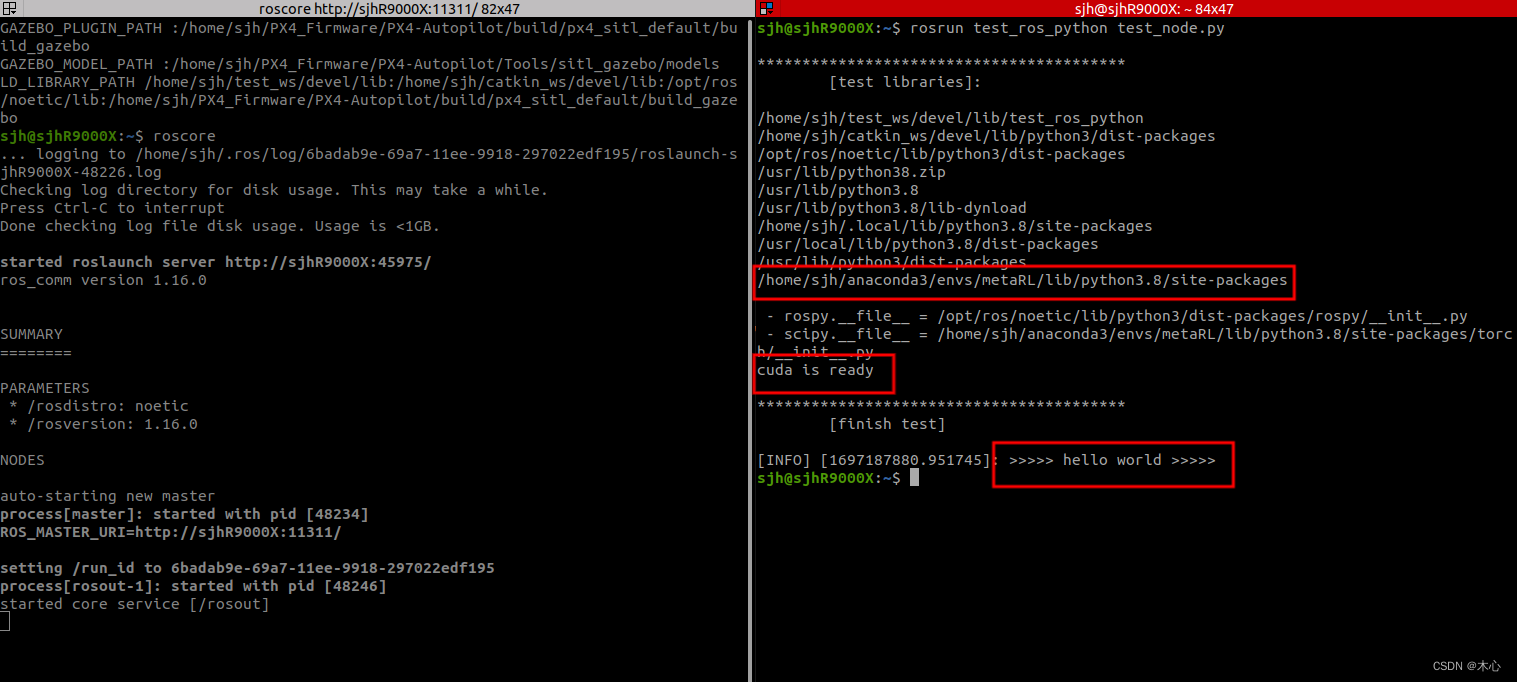
【ROS】ros-noetic和anaconda联合使用【教程】
【ROS】ros-noetic和anaconda联合使用【教程】 文章目录 【ROS】ros-noetic和anaconda联合使用【教程】1. 安装anaconda2. 创建虚拟环境3. 查看python解释器路径4. 在虚拟环境中使用任意的包5. 创建工作空间和ros功能包进行测试Reference 1. 安装anaconda 在Ubuntu20.04中安装…...

自动化RPA开发 --获取所有窗口信息和进程信息
场景 准备做一个RPA工具,可以从桌面和浏览器选择元素,获取窗口信息和进程信息是必要的,因为获取了窗口信息和进程,可用对程序做一些想要的操作。 coding 工具类 /*** Windows系统工具类*/ public class WinOsUtils {static fi…...

【Qt之布局】QVBoxLayout、QHBoxLayout、QGridLayout、QFormLayout介绍及使用
在Qt中,布局管理器(Layout)用于管理窗口中的控件的位置和大小,以适应不同大小的窗口。 常用的布局管理器包括QVBoxLayout、QHBoxLayout、QGridLayout和QFormLayout。 先放张布局UI: 1. QVBoxLayout(垂直布…...
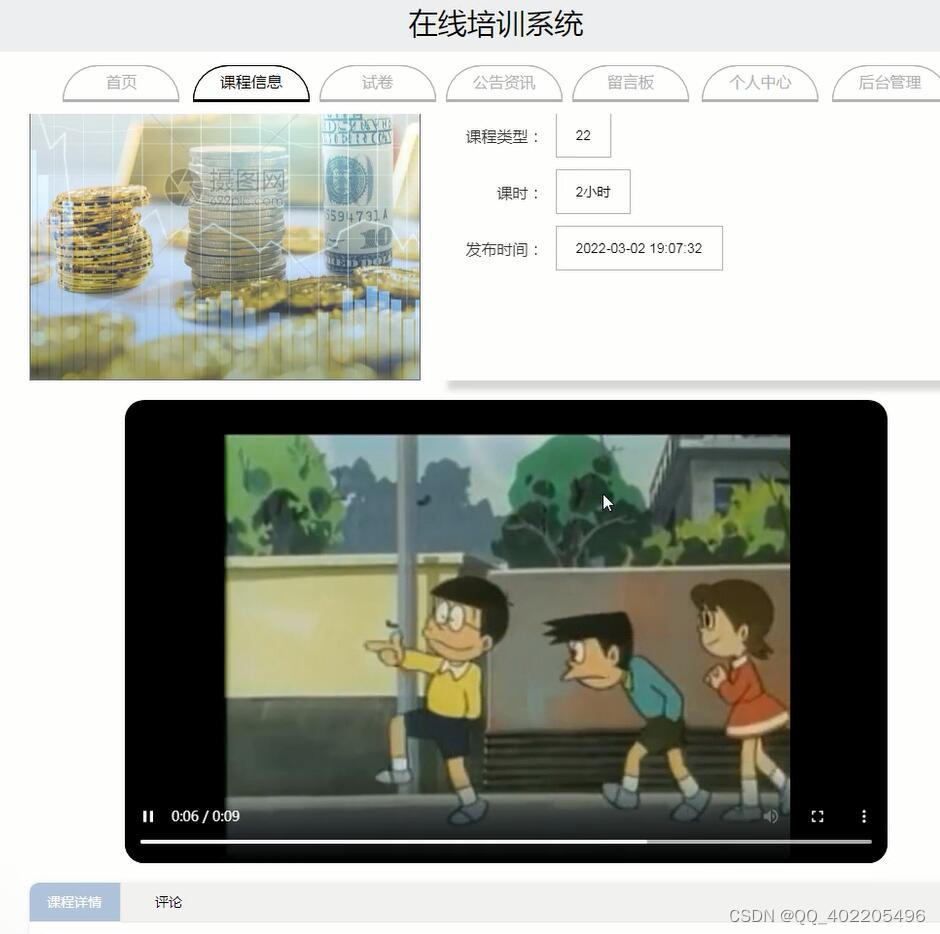
【计算机毕业设计】python在线课程培训学习考试系统637r7-PyCharm项目
使用说明 使用Navicat或者其它工具,在mysql中创建对应名称的数据库,并导入项目的sql文件; 使用PyCharm 导入项目,修改配置,运行项目; 将项目中config.ini配置文件中的数据库配置改为自己的配置,…...
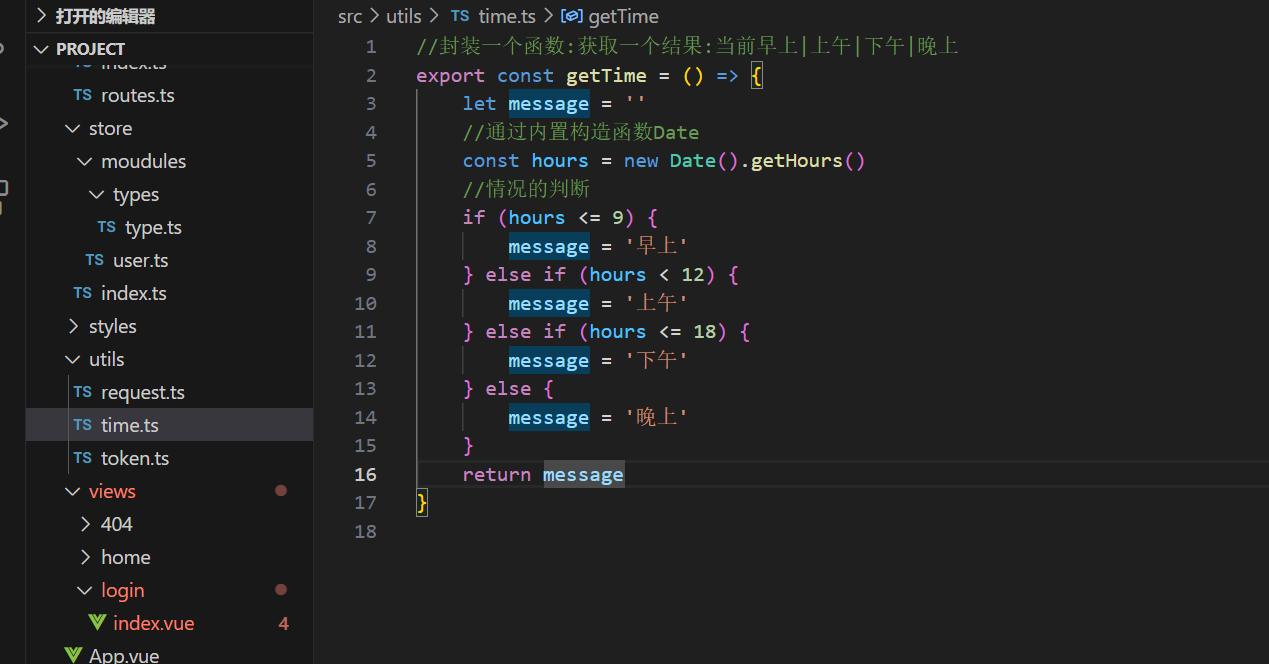
vue3后台管理系统之登录界面和业务的实现
1.静态页面的搭建 <template><div class"login_container"><el-row><el-col :span"12" :xs"0" /><el-col :span"12" :xs"24"><!-- 登录的表单 --><el-form ref"loginForms&qu…...
GEE19:基于Landsat8的常见的植被指数逐年获取
植被指数逐年获取 1. 常见的植被指数1.1 比值植被指数(Ratio vegetation index,RVI)1.2 归一化植被指数(Normalized Difference Vegetation Index,NDVI)1.3 增强植被指数(Enhanced Vegetation I…...

Python【多分支实际应用的练习】
要求:某商店T恤的价格为35元/件(2件9折,3件以上8折),裤子的价格为120 元/条(2条以上9折)小明在该店买了3件T恤和2条裤子,请计算并显示小明应该付多少钱? 代码如下: tshirt_price 35 # T恤的单价 pan…...

LeetCode 343. 整数拆分(动态规划)
LeetCode 343. 整数拆分 思路: 通过题目我们可以知道,一个正整数最少拆成2个数,最多拆成n个数,即可拆分的个数为2~n 若将拆除的第一个正整数令为k,那么剩下的数则为n-k,此时可以不拆分&#x…...
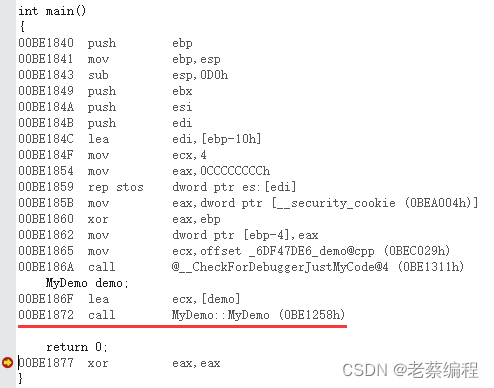
C++对象模型(12)-- 构造函数语义学:构造函数
1、默认构造函数生成规则 编译器不一定会为类生成默认构造函数,但在下列情况下,编译器会生成默认构造函数。 (1)该类没有任何构造函数,但包含一个类类型的成员变量,且成员变量所属的类有默认构造函数。 …...

[23] T^3Bench: Benchmarking Current Progress in Text-to-3D Generation
3D生成蓬勃发展,主流方法通过事例比较和用户调查来评价方法好坏,缺少客观比较指标;本文提出Bench,首次综合比较了不同生成方法;具体来说,本文设计了质量评估(Quality Assessment)和对…...

linux系统如何定时关机
立刻关机 poweroff 10分钟后自动关机 shutdown -h 10 如果希望终止上面执行的10分钟关机,则执行: shutdown -c 希望在22:00关闭计算机 shutdown -h 22:00...
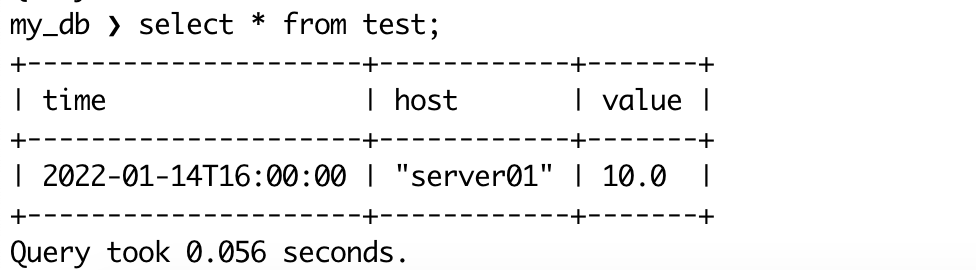
构建高性能物联网数据平台:EMQX和CnosDB的完整教程
CnosDB 是一款高性能、高压缩率、高易用性的开源分布式时序数据库。主要应用场景为物联网、工业互联网、车联网和IT运维。所有代码均已在GitHub开源。本文将介绍如何使用EMQX 这一MQTT 服务器 CnosDB 构建物联网数据平台,实现物联网数据的实时流处理。 前言 在物联…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
