NEFU离散数学实验2-容斥原理
相关概念
离散数学中的容斥原理是一种使用集合运算的技巧,通常用于计算两个或更多集合的并集或交集的大小。以下是一些与容斥原理相关的常见概念和公式。
概念:
1. 集合:由元素组成的对象,通常用大写字母表示,如A、B、C等。
2. 元素:集合中的单个对象,通常用小写字母表示,如a、b、c等。
3. 包含关系:如果一个集合A的所有元素都在另一个集合B中,那么称A是B的子集(或包含于B),用A⊆B表示。
4. 交集:两个集合A和B的交集是由同时属于A和B的元素组成的集合,用A∩B表示。
5. 并集:两个集合A和B的并集是由属于A或B(或同时属于A和B)的元素组成的集合,用A∪B表示。
6. 补集:集合A的补集是由不属于A的元素组成的集合,用Ac表示。
公式:
1. 容斥原理公式:对于两个集合A和B,有:
|A ∪ B| = |A| + |B| - |A ∩ B|
其中,|A|表示集合A的元素个数,|A∪B|表示集合A和B的并集的元素个数,|A∩B|表示集合A和B的交集的元素个数。
2. 三个集合的容斥原理公式:对于三个集合A、B和C,有:
|A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|
其中,|A|表示集合A的元素个数,|A∪B∪C|表示集合A、B和C的并集的元素个数,|A∩B|表示集合A和B的交集的元素个数,以此类推。
1. (程序题)错排
在n个字母的全排列中,使得每个字母都不在原来位置的排列数是多少?请使用错位排列的递推公式来计算本题。
Input
输入数据有多组,每组有1个正整数n(1<=n<=10),代表字母的个数。
Output
在一行内输出这n个字母都不在原来位置的方法数。
Sample Input
2
Sample Output
1
#include <iostream>using namespace std;long long jiecheng(int n)
{long long x = 1;for (int i = 2; i <= n; i++){x *= i;}return x;
}int main()
{int n;while (cin >> n){long long sum = 0;for (int i = 2; i <= n; i++){long long x = jiecheng(n) / jiecheng(i);sum += (i % 2 == 0) ? x : -x;}cout << sum << endl;}return 0;
}
错位排列的递推公式是:
D(n) = (n-1) * (D(n-1) + D(n-2))
其中,D(n)表示n个元素的错位排列的个数。
公式的含义是,将第n个元素固定在某个位置上,那么剩下的n-1个元素的错位排列个数为D(n-1);将第n个元素固定在其他位置上,那么剩下的n-1个元素的错位排列个数为D(n-2)。所以,将这两种情况相加,并乘以(n-1),即可得到n个元素的错位排列个数。
根据这个公式,可以通过递推的方式计算错位排列的个数。初始条件为D(1) = 0, D(2) = 1。
2. (程序题)欧拉函数值
对于一个正整数n,求出它的欧拉函数值,其中1<n<=100000000
Input
输入数据有多组,每组数据一行,有1个正整数为n。
Output
输出n的欧拉函数的值
Sample Input
5
100
Sample Output
4
40
#include <iostream>using namespace std;int eulerPhi(int n) {int result = n;for (int i = 2; i * i <= n; i++) {if (n % i == 0) {while (n % i == 0)n /= i;result -= result / i;}}if (n > 1)result -= result / n;return result;
}int main() {int n;while (cin >> n) {int phi = eulerPhi(n);cout << phi << endl;}return 0;
}
欧拉函数,也称为φ函数,表示小于等于n且与n互质的正整数的个数。其中,互质的定义是两个数的最大公约数为1。
欧拉函数的公式为:
φ(n) = n × (1 - 1/p1) × (1 - 1/p2) × ... × (1 - 1/pk)
其中,n是正整数,p1, p2, ..., pk是n的所有质因数。这个公式的意义是,将n分解为质因数的乘积,然后对于每个质因数pi,将n中所有包含pi的因子都去掉,剩下的因子个数就是与n互质的正整数个数。最后将所有质因数的贡献相乘,就得到了欧拉函数的值。
例如,对于n=10,它的质因数分解为10=2×5,因此有:
φ(10) = 10 × (1 - 1/2) × (1 - 1/5) = 4
即小于等于10且与10互质的正整数个数为4,它们是1、3、7、9。
3. (程序题)考新郎
国庆期间,省城HZ刚刚举行了一场盛大的集体婚礼,为了使婚礼进行的丰富一些,司仪临时想出了有一个有意思的节目,叫做"考新郎",具体的操作是这样的:首先,给每位新娘打扮得几乎一模一样,并盖上大大的红盖头随机坐成一排;然后,让各位新郎寻找自己的新娘.每人只准找一个,并且不允许多人找一个.最后,揭开盖头,如果找错了对象就要当众跪搓衣板...看来做新郎也不是容易的事情...假设一共有N对新婚夫妇,其中有M个新郎找错了新娘,求发生这种情况一共有多少种可能.
Input
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C行数据,每行包含两个整数N和M(1<M<=N<=40)。
Output
对于每个测试实例,请输出一共有多少种发生这种情况的可能,每个实例的输出占一行。
Sample Input
2
2 2
3 2
Sample Output
1
3
#include <iostream>using namespace std;long long jiecheng(int n){int x=1,i;while(n!=0){x=x*n;n--;}return x;}int main(){long long n,sum,flag,i,x,result,N,M,j;long long a[45][45]={0};a[1][1]=a[1][0]=1;for (i = 2; i < 41; i++){for (j = 0; j <= i; j++){if (j == 0)a[i][j] = 1;elsea[i][j] = a[i - 1][j - 1] + a[i - 1][j];}}cin>>n;for(j=0;j<n;j++){cin>>N>>M;sum=0;flag=1;for(i=2;i<=M;i++){x=jiecheng(M)/jiecheng(i);sum=sum+flag*x;flag=flag*(-1);}result=sum*a[N][M];cout<<result<<endl;}return 0;
}利用容斥原理,我们可以将问题转化为求解有多少种情况满足至少有一个新郎找错的情况,然后再减去有两个新郎找错的情况,再加上有三个新郎找错的情况,依此类推,直到加上有M个新郎找错的情况。
首先,考虑只有一个新郎找错的情况。假设第i个新郎找错了新娘,那么他有N-1种选择,剩下的N-1对夫妇中有M-1对新郎找错。所以,只有一个新郎找错的情况一共有C(N-1,1) * C(N-1, M-1)种可能。
然后,考虑有两个新郎找错的情况。假设第i个新郎和第j个新郎找错了新娘,那么他们有N-2种选择,剩下的N-2对夫妇中有M-2对新郎找错。所以,有两个新郎找错的情况一共有C(N-2,2) * C(N-2, M-2)种可能。
依此类推,我们可以得到有k个新郎找错的情况一共有C(N-k,k) * C(N-k, M-k)种可能。
最后,我们将所有情况累加起来,就可以得到发生这种情况的总数。
相关文章:

NEFU离散数学实验2-容斥原理
相关概念 离散数学中的容斥原理是一种使用集合运算的技巧,通常用于计算两个或更多集合的并集或交集的大小。以下是一些与容斥原理相关的常见概念和公式。 概念: 1. 集合:由元素组成的对象,通常用大写字母表示,如A、B、…...
解决Windows内存溢出/占满死机问题-PoolMon工具
某一天, 工作所用笔记本突然越来越卡直至死机 以为只是windows11的抽风行为,之前就因为windows11资源管理器经常卡死(后升级小版本好多了)。 遂长按电源键强制关机重启。 然慢慢又越来越卡,直至卡死,无…...
【ROS】ros-noetic和anaconda联合使用【教程】
【ROS】ros-noetic和anaconda联合使用【教程】 文章目录 【ROS】ros-noetic和anaconda联合使用【教程】1. 安装anaconda2. 创建虚拟环境3. 查看python解释器路径4. 在虚拟环境中使用任意的包5. 创建工作空间和ros功能包进行测试Reference 1. 安装anaconda 在Ubuntu20.04中安装…...

自动化RPA开发 --获取所有窗口信息和进程信息
场景 准备做一个RPA工具,可以从桌面和浏览器选择元素,获取窗口信息和进程信息是必要的,因为获取了窗口信息和进程,可用对程序做一些想要的操作。 coding 工具类 /*** Windows系统工具类*/ public class WinOsUtils {static fi…...

【Qt之布局】QVBoxLayout、QHBoxLayout、QGridLayout、QFormLayout介绍及使用
在Qt中,布局管理器(Layout)用于管理窗口中的控件的位置和大小,以适应不同大小的窗口。 常用的布局管理器包括QVBoxLayout、QHBoxLayout、QGridLayout和QFormLayout。 先放张布局UI: 1. QVBoxLayout(垂直布…...
【计算机毕业设计】python在线课程培训学习考试系统637r7-PyCharm项目
使用说明 使用Navicat或者其它工具,在mysql中创建对应名称的数据库,并导入项目的sql文件; 使用PyCharm 导入项目,修改配置,运行项目; 将项目中config.ini配置文件中的数据库配置改为自己的配置,…...
vue3后台管理系统之登录界面和业务的实现
1.静态页面的搭建 <template><div class"login_container"><el-row><el-col :span"12" :xs"0" /><el-col :span"12" :xs"24"><!-- 登录的表单 --><el-form ref"loginForms&qu…...
GEE19:基于Landsat8的常见的植被指数逐年获取
植被指数逐年获取 1. 常见的植被指数1.1 比值植被指数(Ratio vegetation index,RVI)1.2 归一化植被指数(Normalized Difference Vegetation Index,NDVI)1.3 增强植被指数(Enhanced Vegetation I…...

Python【多分支实际应用的练习】
要求:某商店T恤的价格为35元/件(2件9折,3件以上8折),裤子的价格为120 元/条(2条以上9折)小明在该店买了3件T恤和2条裤子,请计算并显示小明应该付多少钱? 代码如下: tshirt_price 35 # T恤的单价 pan…...

LeetCode 343. 整数拆分(动态规划)
LeetCode 343. 整数拆分 思路: 通过题目我们可以知道,一个正整数最少拆成2个数,最多拆成n个数,即可拆分的个数为2~n 若将拆除的第一个正整数令为k,那么剩下的数则为n-k,此时可以不拆分&#x…...
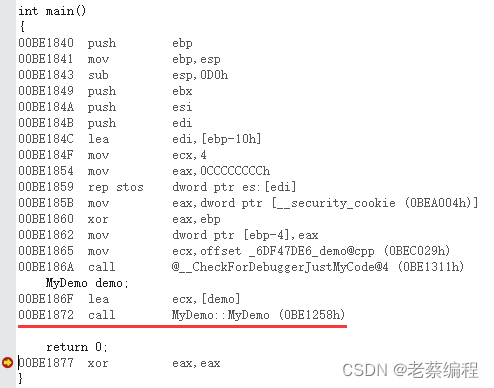
C++对象模型(12)-- 构造函数语义学:构造函数
1、默认构造函数生成规则 编译器不一定会为类生成默认构造函数,但在下列情况下,编译器会生成默认构造函数。 (1)该类没有任何构造函数,但包含一个类类型的成员变量,且成员变量所属的类有默认构造函数。 …...

[23] T^3Bench: Benchmarking Current Progress in Text-to-3D Generation
3D生成蓬勃发展,主流方法通过事例比较和用户调查来评价方法好坏,缺少客观比较指标;本文提出Bench,首次综合比较了不同生成方法;具体来说,本文设计了质量评估(Quality Assessment)和对…...

linux系统如何定时关机
立刻关机 poweroff 10分钟后自动关机 shutdown -h 10 如果希望终止上面执行的10分钟关机,则执行: shutdown -c 希望在22:00关闭计算机 shutdown -h 22:00...
构建高性能物联网数据平台:EMQX和CnosDB的完整教程
CnosDB 是一款高性能、高压缩率、高易用性的开源分布式时序数据库。主要应用场景为物联网、工业互联网、车联网和IT运维。所有代码均已在GitHub开源。本文将介绍如何使用EMQX 这一MQTT 服务器 CnosDB 构建物联网数据平台,实现物联网数据的实时流处理。 前言 在物联…...

【vim 学习系列文章 11 -- vim filetype | execute | runtimepath 详细介绍】
文章目录 filetype plugin indent on 什么功能?vim runtimepath 详细介绍vim 中 execute 命令详细介绍execute pathogen#infect() 详细介绍 filetype plugin indent on 什么功能? 在网上我们经常可以看到vimrc配置中有 filetype plugin indent on 这个配…...

[备忘]WindowsLinux上查看端口被什么进程占用|端口占用
Windows上 查看端口占用: netstat -aon|findstr <端口号> 通过进程ID查询进程信息 tasklist | findstr <上一步查出来的进程号> 图例: Linux 上 查看端口占用: netstat -tuln | grep <端口号> lsof -i:<端口号&…...

函数的扩展
文章目录 函数的扩展1.函数参数的默认值1.1 基本用法-- 参数变量是默认声明的,所以不能用 let或const 再次声明-- 使用参数默认值时,函数不能有同名参数1.2 与解构赋值默认值结合使用☆☆☆ 函数参数的默认值生效以后,参数解构赋值依然会进行…...
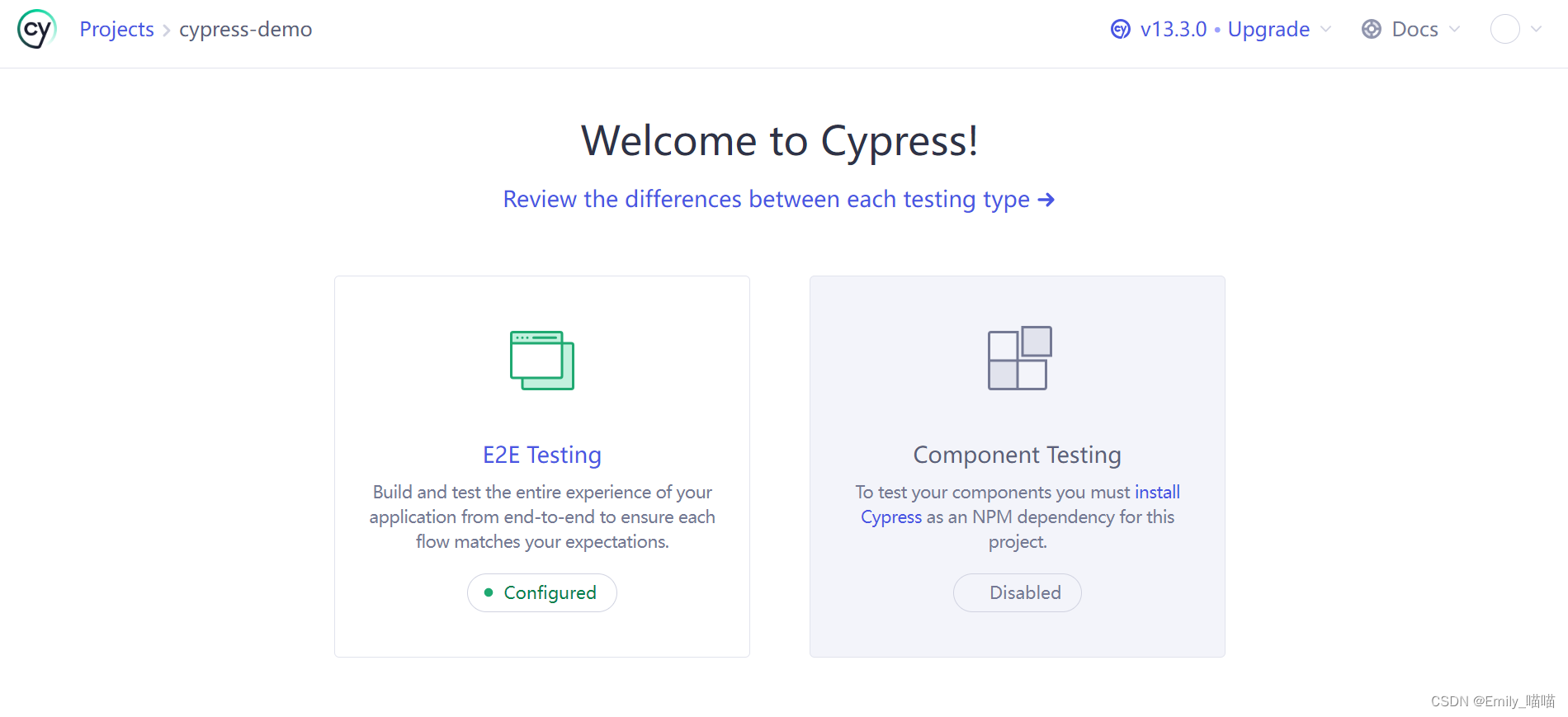
Cypress安装使用
node.js 安装使用Cypress总是会看见node.js,那就先看看node.js是什么。JavaScript以前运行需要在浏览器中(浏览器内置解释器),通过node.js框架内置v8引擎(也就是可以执行js脚本所需的工具),这样…...
怎么把图片改成jpg格式?
怎么把图片改成jpg格式?大家都知道,随着计算机被发明到现在已经存在了很多年,在这么多的的技术发展过程中,也形成了种类非常多的图片文件格式,例如平时我们能接触到的图片格式有jpg、png、gif、bmp、heic、tiff、jfif、…...

[一带一路金砖 2023 CTF]Crypto
题1 题目描述: from Crypto.Util.number import * from flag import flag import gmpy2 assert(len(flag)38) flag bytes_to_long(flag)p getPrime(512) q getPrime(512)e 304 enc pow(flag,e,p*q) print(p) print(q) print(enc) #9794998439882070838464987…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
