[一带一路金砖 2023 CTF]Crypto
题1
题目描述:
from Crypto.Util.number import *
from flag import flag
import gmpy2
assert(len(flag)==38)
flag = bytes_to_long(flag)p = getPrime(512)
q = getPrime(512)e = 304
enc = pow(flag,e,p*q)
print(p)
print(q)
print(enc)
#9794998439882070838464987778400633526071369507639213778760131552998185895297188941828281554258704149333679257014558677504899624597863467726403690826271979
#10684338300287479543408040458978465940026825189952497034380241358187629934633982402116457227553161613428839906159238238486780629366907463456434647021345729
#88310577537712396844221012233266891147970635383301697208951868705047581001657402229066444746440502616020663700100248617117426072580419555633169418185262898647471677640199331807653373089977785816106098591077542771088672088382667974425747852317932746201547664979549641193108900510265622890793400796486146522028
题目分析:
e和phi不互素,同时flag长度比p和q小,故可直接用p或q中其中一个进行解
不互素考点应该是很熟了,这里就不多说咯
exp:
from Crypto.Util.number import *
from gmpy2 import *
e = 304
p = 9794998439882070838464987778400633526071369507639213778760131552998185895297188941828281554258704149333679257014558677504899624597863467726403690826271979
q = 10684338300287479543408040458978465940026825189952497034380241358187629934633982402116457227553161613428839906159238238486780629366907463456434647021345729
c = 88310577537712396844221012233266891147970635383301697208951868705047581001657402229066444746440502616020663700100248617117426072580419555633169418185262898647471677640199331807653373089977785816106098591077542771088672088382667974425747852317932746201547664979549641193108900510265622890793400796486146522028
d = invert(e // 16,(q - 1))
m_16 = pow(c,d,q)
e = 16
R.<x> = Zmod(q)[]
f=x^e-m_16
mps=f.monic().roots()
for i in mps:flag=long_to_bytes(int(i[0]))if b'flag' in flag:print(flag)
# flag{947b6543117e32730a93d1b43c98bc57}
题2
题目描述:
from Crypto.Util.number import *
from flag import flagdef gen_primes(nbit, imbalance):p = 2FACTORS = [p]while p.bit_length() < nbit - 2 * imbalance:factor = getPrime(imbalance)FACTORS.append(factor)p *= factor # 一些小素数的乘积rbit = (nbit - p.bit_length()) // 2while True:r, s = [getPrime(rbit) for _ in '01']_p = p * r * sif _p.bit_length() < nbit: rbit += 1if _p.bit_length() > nbit: rbit -= 1if isPrime(_p + 1): # 光滑FACTORS.extend((r, s))p = _p + 1breakFACTORS.sort()return (p, FACTORS)def genkey(nbit, imbalance, e):while True:p, FACTORS = gen_primes(nbit // 2, imbalance)if len(FACTORS) != len(set(FACTORS)):continueq, q_factors = gen_primes(nbit // 2, imbalance + 1)if len(q_factors) != len(set(q_factors)):continuefactors = FACTORS + q_factorsif e not in factors:breakn = p * qreturn n, (p, q)nbit = 2048
imbalance = 19
e = 0x10001m_1 = bytes_to_long(flag[:len(flag)//2])
m_2 = bytes_to_long(flag[len(flag)//2:])n, PRIMES = genkey(nbit, imbalance, e)
c_1 = pow(m_1, e, n)
c_2 = pow(e, m_2, n)
print('n =', n)
print('c_1 =', c_1)
print('c_2 =', c_2)
n = 35357873937435054001282352637015489837983629944603246522178730306982853403322122532742547568947348720656333165913123004754628275811015219202713548802943693917918541563761339716370762198583591114052428351599691659723508542841656789503328119510785085937979525249694594158534358323126435951391004918101544306531617516774746895733526101034675683422353395313765068796525289210446354001944876249728896374221851147854490650250688040658359437708219708086466006475368143815063574396167110037225787616695794333552173352376965108641554651899828690770801642222911404004972981226404611238384640428742441960433230255967882512572709
c_1 = 16634534464526067333266542688361417073505104370260567430743212030440685317214374585499981030226926044766739869847879031408549807956380355500301201488848875687853416183379064412708949479112570148317905419837975685732979495910124097985791487969870055434863407745827818697689550695419811875635482462317998019001874694405544022096737341305813428625314356741922244350713455318505335210523811539099373597334819062036544344240156834535244078408347762370087901917949527669361716338102428255611527880175371489236975227446140403028949555168795599427303842397557962531520805711901076455900612217613591150327899301858065771562916
c_2 = 28959414058046581387331073805593474819964554400846556519089342566960219426395093378840690033900219718180201586444279902099201314738785482187096282489335039754400853514399233561703766501981317579016015885985249393698030292377653287627063434792453444305041899628924704707327777803327634177387380885834429684833509758496969064593639077614464933018728667369508101718561232112365432775831642293382722453145808785853553029281098760388699782452404701217989853131800383523025244719015821981668238625535719639173942578430758429709476625832809897441275508034910613246129679480731733559701167577051633529935423253203666147846715
题目分析:
第一部分为Pollard’s p-1光滑
直接解
exp:
from Crypto.Util.number import *
from gmpy2 import *
n = 35357873937435054001282352637015489837983629944603246522178730306982853403322122532742547568947348720656333165913123004754628275811015219202713548802943693917918541563761339716370762198583591114052428351599691659723508542841656789503328119510785085937979525249694594158534358323126435951391004918101544306531617516774746895733526101034675683422353395313765068796525289210446354001944876249728896374221851147854490650250688040658359437708219708086466006475368143815063574396167110037225787616695794333552173352376965108641554651899828690770801642222911404004972981226404611238384640428742441960433230255967882512572709
c_1 = 16634534464526067333266542688361417073505104370260567430743212030440685317214374585499981030226926044766739869847879031408549807956380355500301201488848875687853416183379064412708949479112570148317905419837975685732979495910124097985791487969870055434863407745827818697689550695419811875635482462317998019001874694405544022096737341305813428625314356741922244350713455318505335210523811539099373597334819062036544344240156834535244078408347762370087901917949527669361716338102428255611527880175371489236975227446140403028949555168795599427303842397557962531520805711901076455900612217613591150327899301858065771562916
c_2 = 28959414058046581387331073805593474819964554400846556519089342566960219426395093378840690033900219718180201586444279902099201314738785482187096282489335039754400853514399233561703766501981317579016015885985249393698030292377653287627063434792453444305041899628924704707327777803327634177387380885834429684833509758496969064593639077614464933018728667369508101718561232112365432775831642293382722453145808785853553029281098760388699782452404701217989853131800383523025244719015821981668238625535719639173942578430758429709476625832809897441275508034910613246129679480731733559701167577051633529935423253203666147846715
e = 0x10001
def Pollards_p_1(N):n = 2a = 2while True:a = pow(a,n,N)res = gcd(a-1,N)print(n)if res != 1 and res != N:print('p = ',res)return resn += 1
# p = Pollards_p_1(n)
p = 246193986637546903265592815609577026241302357122314925452960382002903884663793124671589668426466042284818011792326340585156178366427487449232598147821980481083788083405892143123015262709410005719036034457206601471709604309275710937299133844390087441265560849989236470128705724138785359931092408727167182527227
q = n // p
d = inverse(e,(p - 1)*(q - 1))
print(long_to_bytes(pow(c_1,d,n))) # flag{5eec62654a551c
之后离散对数,变下域
c_2 = 28959414058046581387331073805593474819964554400846556519089342566960219426395093378840690033900219718180201586444279902099201314738785482187096282489335039754400853514399233561703766501981317579016015885985249393698030292377653287627063434792453444305041899628924704707327777803327634177387380885834429684833509758496969064593639077614464933018728667369508101718561232112365432775831642293382722453145808785853553029281098760388699782452404701217989853131800383523025244719015821981668238625535719639173942578430758429709476625832809897441275508034910613246129679480731733559701167577051633529935423253203666147846715
e = 0x10001
p = 246193986637546903265592815609577026241302357122314925452960382002903884663793124671589668426466042284818011792326340585156178366427487449232598147821980481083788083405892143123015262709410005719036034457206601471709604309275710937299133844390087441265560849989236470128705724138785359931092408727167182527227
G = Zmod(p)
print(long_to_bytes(ZZ(discrete_log(G(c_2),G(e))))) # 8cb2280fe9405f908f}
关键词:离散对数变域
唉,都是出的原题啊。不过没事,还是学到了一个没接触过的小点
相关文章:

[一带一路金砖 2023 CTF]Crypto
题1 题目描述: from Crypto.Util.number import * from flag import flag import gmpy2 assert(len(flag)38) flag bytes_to_long(flag)p getPrime(512) q getPrime(512)e 304 enc pow(flag,e,p*q) print(p) print(q) print(enc) #9794998439882070838464987…...

FPGA【Verilog语法】
关键字: and always assign begin buf bufif0 bufif1 case casex casez cmos deassign default defparam disable edge else end endcase endfunction endprimitive endmodule endspecify endtable …...

Flume 整合 Kafka
1.背景 先说一下,为什么要使用 Flume + Kafka? 以实时流处理项目为例,由于采集的数据量可能存在峰值和峰谷,假设是一个电商项目,那么峰值通常出现在秒杀时,这时如果直接将 Flume 聚合后的数据输入到 Storm 等分布式计算框架中,可能就会超过集群的处理能力,这时采用 Kaf…...
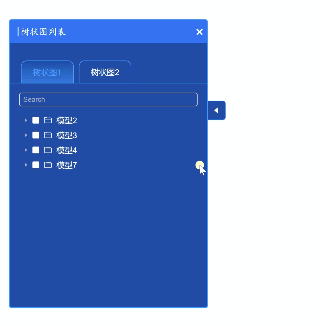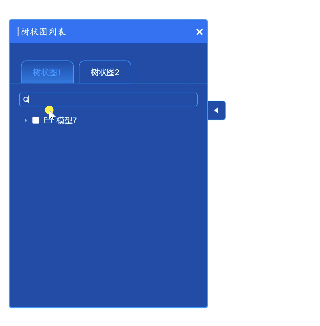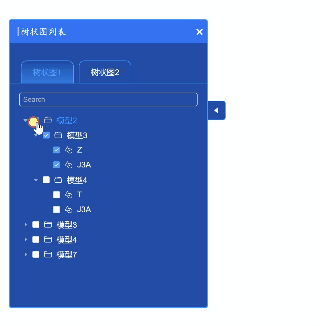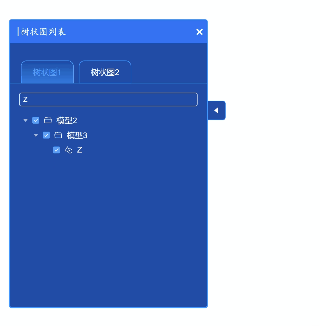
VUE:侧边弹出栏组件,组件中有树状图,搜索框可筛选树状图节点,可收缩
作者:CSDN @ _乐多_ 本文记录了一个侧边弹出栏组件代码。代码即插即用。 弹出栏中有树状图,搜索框,可收缩。 其中,搜索框可筛选树状图节点。点击右侧小按钮可以收缩弹出框,点击X号也可以收缩弹出框。 文章目录 一、组件代码代码依赖element-plus库。且需要下载几个svg图…...
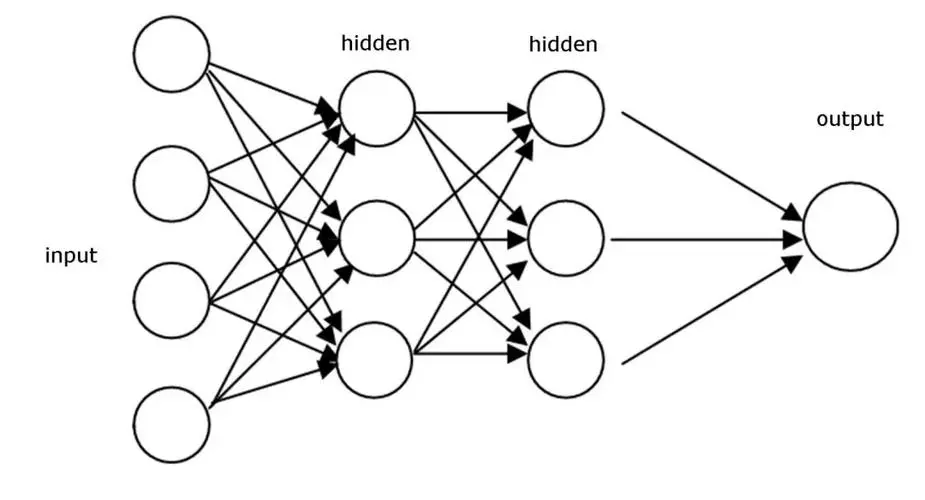
如何使用pytorch定义一个多层感知神经网络模型——拓展到所有模型知识
# 导入必要的库 import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader, random_split import torchvision.transforms as transforms import torchvision.datasets as datasets# 定义MLP模型 class MLP(nn.Module):def __…...
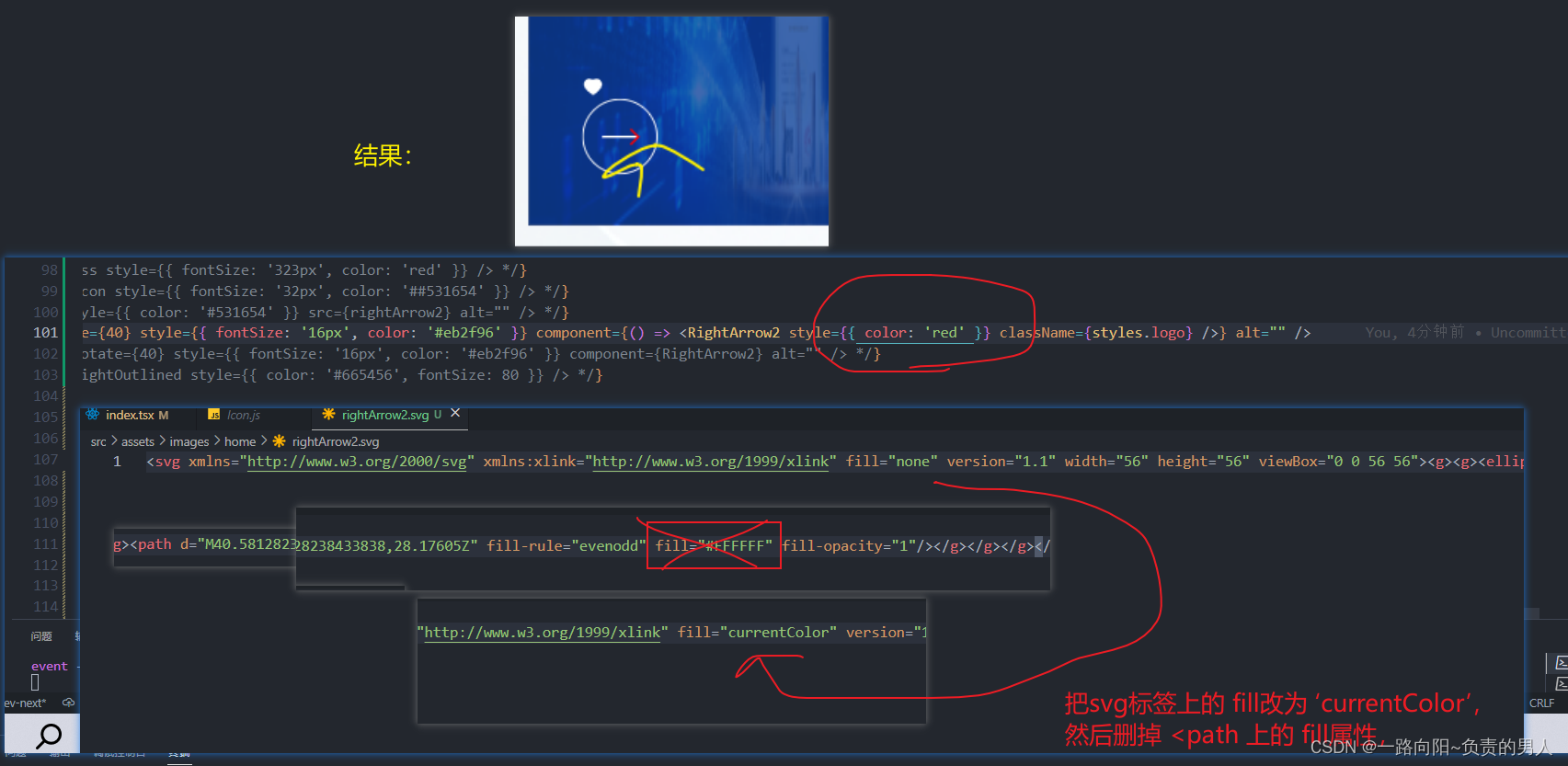
为什么引入SVG文件,给它定义属性不生效原理分析
背景: 我使用antd 的Icon组件引入SVG图片,但给svg图片定义styles样式时,不生效,为什么呢? 我们平时用antd组件库的 < ArrowRightOutlined style{{color: red }}>时为什么会生效呢,但我图一这样定义就…...

Integer包装类常用方法和属性
包装类 什么是包装类Integer包装类常用方法和属性 什么是包装类 Java 包装类是指为了方便处理基本数据类型而提供的对应的引用类型。Java 提供了八个基本数据类型(boolean、byte、short、int、long、float、double、char),每个基本数据类型对…...

基于Spring boot轻松实现一个多数据源框架
Spring Boot 提供了 Data JPA 的包,允许你使用类似 ORM 的接口连接到 RDMS。它很容易使用和实现,只需要在 pom.xml 中添加一个条目(如果使用的是 Maven,Gradle 则是在 build.gradle 文件中)。 <dependencies>&l…...

vue前端实现打印功能并约束纸张大小---调用浏览器打印功能打印页面部分元素并固定纸张大小
需求是打印指定div实现小票打印功能。调用浏览器的自带打印功能只能实现打印可视区域,所以这里采用截图新窗口打开打印去实现此需求。 1.安装html2canvas库实现截图功能 npm install html2canvas --save2.在需要进行截图和打印的组件中,引入html2canvas…...

音乐播放器蜂鸣器ROM存储歌曲verilog,代码/视频
名称:音乐播放器蜂鸣器ROM存储歌曲 软件:Quartus 语言:Verilog 代码功能: 设计音乐播放器,要求至少包含2首歌曲,使用按键切换歌曲,使用开发板的蜂鸣器播放音乐,使用Quartus内的RO…...
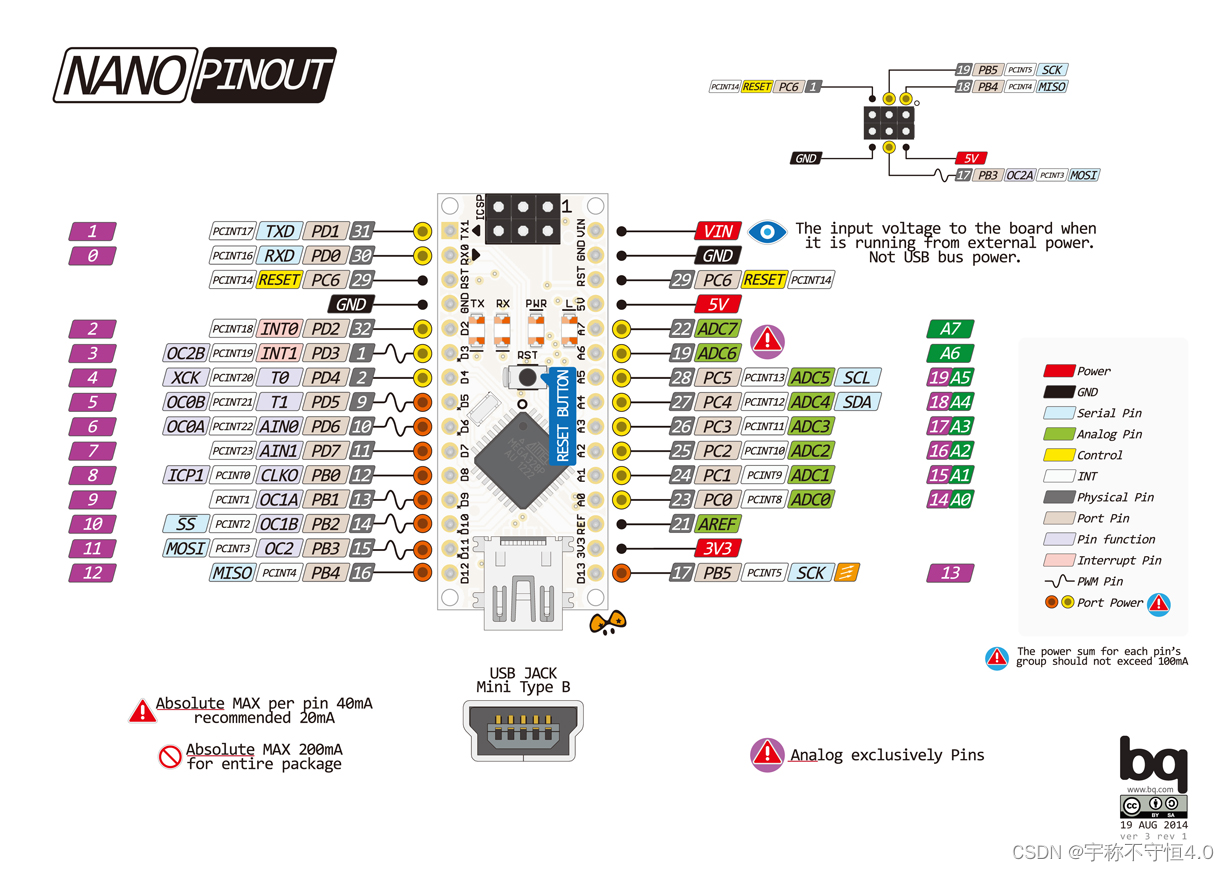
Arduino Nano 引脚复用分析
近期开发的项目为气体传感器采集仪,综合需求,选取NANO作为主控,附属设备有 oled、旋转编码器、H桥板、蠕动泵、开关、航插等,主要是用现有接口怎么合理配置实现功能。 不管stm32 还是 Arduino 都要看清引脚图 D2 D3 引脚是两个外…...

Go 函数多返回值错误处理与error 类型介绍
Go 函数多返回值错误处理与error 类型介绍 文章目录 Go 函数多返回值错误处理与error 类型介绍一、error 类型与错误值构造1.1 Error 接口介绍1.2 构造错误值的方法1.2.1 使用errors包1.2.2 自定义错误类型 二、error 类型的好处2.1 第一点:统一了错误类型2.2 第二点…...

数论分块
本质就是利用取整分数值的块状分布。 UVA11526 H(n) 题意: 求 ∑ i 1 n n i \sum_{i1}^{n} \frac {n}{i} ∑i1nin。 解析: ⌊ n i ⌋ \lfloor \frac{n}{i} \rfloor ⌊in⌋ 只有 O ( n ) O(\sqrt n) O(n ) 种取值,考虑将相同值同…...

宏任务与微任务,代码执行顺序
js引擎工作进程是同步的。事件循环机制,事件队列。 脚本代码执行顺序,是先执行同步代码,遇到微任务,就把它推进任务队列中。每个宏任务完成后,再执行下一个宏任务。 宏任务有哪些: i/o读写 定时器setTi…...

正方形(Squares, ACM/ICPC World Finals 1990, UVa201)rust解法
有n行n列(2≤n≤9)的小黑点,还有m条线段连接其中的一些黑点。统计这些线段连成了多少个正方形(每种边长分别统计)。 行从上到下编号为1~n,列从左到右编号为1~n。边用H i j和V i j表示…...

【算法设计与分析qwl】伪码——顺序检索,插入排序
伪代码: 例子: 改进的顺序检索 Search(L,x)输入:数组L[1...n],元素从小到大排序,数x输出:若x在L中,输出x位置下标 j ,否则输出0 j <- 1 while j<n and x>L[j] do j <- j1 if x<…...

Uniapp路由拦截-自定义路由白名单
步骤一:新建routerIntercept.js文件 步骤二:routerIntercept文件中写入:(根据自己需要修改whiteList白名单中的页面路径和自己的逻辑处理) import Vue from vue // 白名单 const whiteList = [/pages/public/login,/pages/public/privacyAgreement, ]export default asy…...
在中国可以使用 HubSpot 吗?
当谈到市场营销和客户关系管理工具时,HubSpot通常是一家企业的首选。然而,对于许多中国的企业来说,一个重要的问题是:在中国可以使用HubSpot吗?这个问题涉及到不同的方面,包括政策法规、社交媒体平台、语言…...

Java的基础应用
Java是一种广泛应用于软件开发的编程语言,基础应用涵盖了很多方面。以下是Java的一些基础应用方面的介绍: 1. 控制流语句:Java中的程序流程控制语句分为选择语句和循环语句。选择语句包括if-else语句和switch语句,循环语句包括fo…...
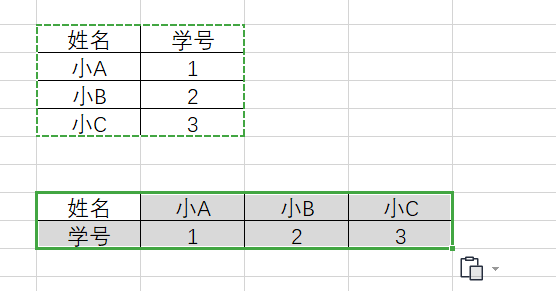
【excel】列转行
列转行 工作中有一些数据是列表,现在需要转行 选表格内容:在excel表格中选中表格数据区域。点击复制:在选中表格区域处右击点击复制。点击选择性粘贴:在表格中鼠标右击点击选择性粘贴。勾选转置:在选择性粘勾选转置选…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...
