【数据结构】排序算法的稳定性分析

💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页 :阿然成长日记 👈点击可跳转
📆 个人专栏: 🔹数据结构与算法🔹C语言进阶
🚩 不能则学,不知则问,耻于问人,决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍
文章目录
- 一、稳定性的定义:
- 二、排序稳定性的分析:
- (1)冒泡排序
- (2)选择排序
- (3)插入排序
- (4)快速排序
- (5)归并排序
- (6)基数排序
- (7)希尔排序
- (8)堆排序
- 排序算法规律总结:
前言:
前面我们已经学习了八大排序的所有算法,本篇主要讲解每个算法的稳定度推理。
一、稳定性的定义:
例如:一个人的性格很稳定。或是这个人做事的时间很稳定,稳定指的是他做事有着自己固定的速度,而不是越稳定做事越快或越慢。这是我们生活中所理解的稳定。
相同的两个数据排序后,如果相对位置不发生变化,就是稳定的;反之,如果相对位置发生变化,就是不稳定的。
🚩举个例子:
假设小组成员一共A,B,C,D四人,通过一次考试来对他们进行排名。
我们使用一个队列来存储他们的提交顺序:
提交顺序依次是 A,B,C,D
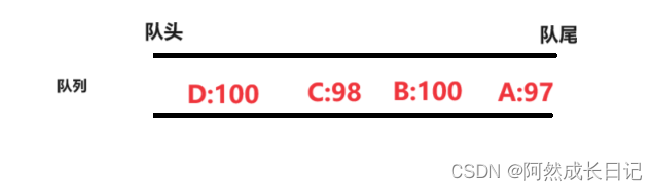
提交完毕,需要对他们进行排序,在这里注意,相同的分数下,通过比较提交的先后次序确定排名。
🔸如果这个排序算法是稳定的,那么排序的次序应该是B,D,C,A; B和D的相对位置先后顺序没有改变。
🔸如果这个排序算法是不稳定的,那么排序的次序应该是D,B,C,A; B和D的相对位置先后顺序改变。
由上可以发现,稳定的算法可以确保排名的准确性。
二、排序稳定性的分析:
(1)冒泡排序
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,是不会执行交换操作的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
(2)选择排序
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n - 1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法。
(3)插入排序
插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。然后是第二个元向前比较,第三个~~;比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
(4)快速排序
以单趟排序是霍尔排序为例,快速排序有两个方向,左边的i下标一直往右走,当a[i] <= a[key],其中key是中枢元素的数组下标,一般取为数组的首元素。而右边的j下标一直往左走,当a[j] > a[key]。如果i和j都走不动了,i <= j,交换a[i]和a[j],重复上面的过程,直到i > j。 交换a[j]和a[center_index],完成一趟快速排序。在中枢元素和a[j]交换的时候,很有可能把前面的元素的稳定性打乱,比如序列为5 3 3 4 3 8 9 10 11,现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱,所以快速排序是一个不稳定的排序算法,不稳定发生在中枢元素和a[j] 交换的时刻。
(5)归并排序
归并排序是把一个序列通过递归地分成短序列,直至分到每组只剩一个元素停止,开始并,从只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的一段段的序列合并成一个有序的长序列,不断合并直到原序列全部排好序。可以发现,在1个或2个元素时,1个元素不会交换,2个元素如果大小相等也不会i交换,这不会破坏稳定性。那么,在短的有序序列合并过程中我们可以保证如果两个当前元素相等时,我们把处在前面的序列的元素保存在结果序列的前面,这样就保证了稳定性。所以,归并排序也是稳定的排序算法。
(6)基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序,最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以,归并排序也是稳定的排序算法。
(7)希尔排序
希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,所以插入排序的元素个数很少,速度很快;当元素基本有序了,步长很小, 插入排序对于有序的序列效率很高。所以,希尔排序的时间复杂度会比O(n^2)好一些。由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以希尔排序是不稳定的。
(8)堆排序
我们知道堆的结构是节点i的孩子为2 * i和2 * i + 1节点,大顶堆要求父节点大于等于其2个子节点,小顶堆要求父节点小于等于其2个子节点。在一个长为n 的序列,堆排序的过程是从第n / 2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n / 2 - 1, n / 2 - 2, … 1这些个父节点选择元素时,就会破坏稳定性。有可能第n / 2个父节点交换把后面一个元素交换过去了,而第n / 2 - 1个父节点把后面一个相同的元素没 有交换,那么这2个相同的元素之间的稳定性就被破坏了。所以,堆排序不是稳定的排序算法。
📜综上,得出结论:
🔸不是稳定的排序算法: 选择排序、快速排序、希尔排序、堆排序
🔸稳定的排序算法: 冒泡排序、插入排序、归并排序和,基数排序

排序算法规律总结:
快排: 初始顺序影响较大,有序是,性能最差
插入, 冒泡 : 接近有序,性能最好
希尔:希尔是对插入排序的优化,这种优化是在无序的序列中才有明显的效果,如果序列接近有序,反而是插入最优。
堆排,归并,选择对初始顺序不敏感
相关文章:

【数据结构】排序算法的稳定性分析
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
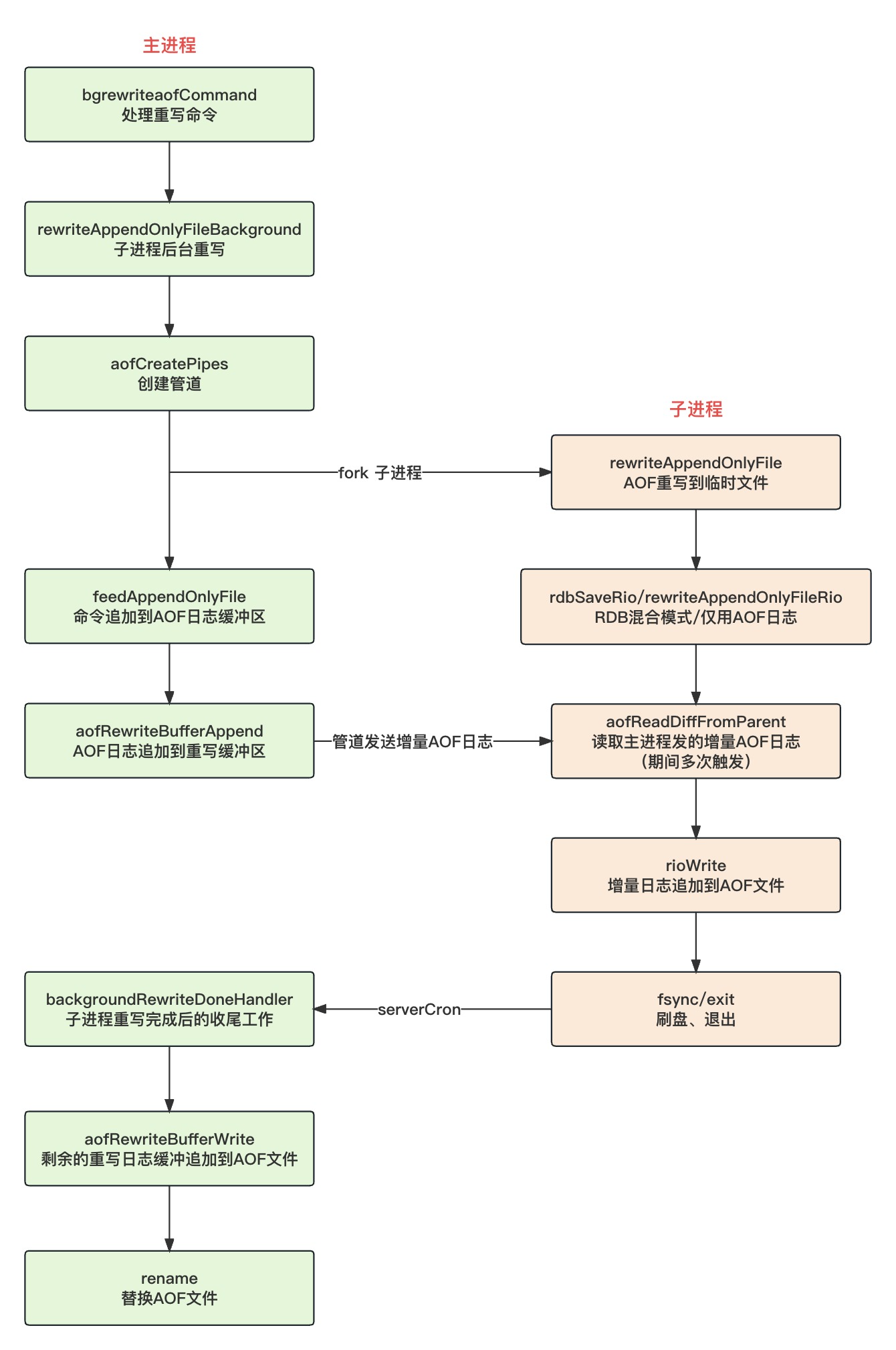
Redis AOF持久化和ReWrite
前言 Redis 的 RDB 持久化机制简单直接,把某一时刻的所有键值对以二进制的方式写入到磁盘,特点是恢复速度快,尤其适合数据备份、主从复制场景。但如果你的目的是要保证数据可靠性,RDB 就不太适合了,因为 RDB 持久化不…...
Flink学习之旅:(一)Flink部署安装
1.本地搭建 1.1.下载Flink 进入Flink官网,点击Downloads 往下滑动就可以看到 Flink 的所有版本了,看自己需要什么版本点击下载即可。 1.2.上传解压 上传至服务器,进行解压 tar -zxvf flink-1.17.1-bin-scala_2.12.tgz -C ../module/ 1.3.启…...

Go语言入门心法(六): HTTP面向客户端|服务端编程
Go语言入门心法(一): 基础语法 Go语言入门心法(二): 结构体 Go语言入门心法(三): 接口 Go语言入门心法(四): 异常体系 Go语言入门心法(五): 函数 一:go语言面向web编程认知 Go语言的最大优势在于并发与性能,其性能可以媲美C和C,并发在网络编程中更是至关重要 使用http发送请…...

为什么非const静态成员变量一定要在类外定义
当我们如下声明了一个类: class A{public:static int sti_data;// 这个语句在c11前不能通过编译,在c11的新标准下,已经能够在声明一个普通变量是就对其进行初始化。int a 10;static const int b 1;//...其他member };// 在类外…...

千兆光模块和万兆光模块的区别?
在网络通信领域,千兆光模块和万兆光模块是最为常见且广泛应用的两种光模块。不同之处在于传输速率、封装、传输距离、功耗、发射光功率、接收光功率和应用场景等。 千兆光模块的传输速率为1 Gbps,万兆光模块的传输速率为10 Gbps,这意味着万…...
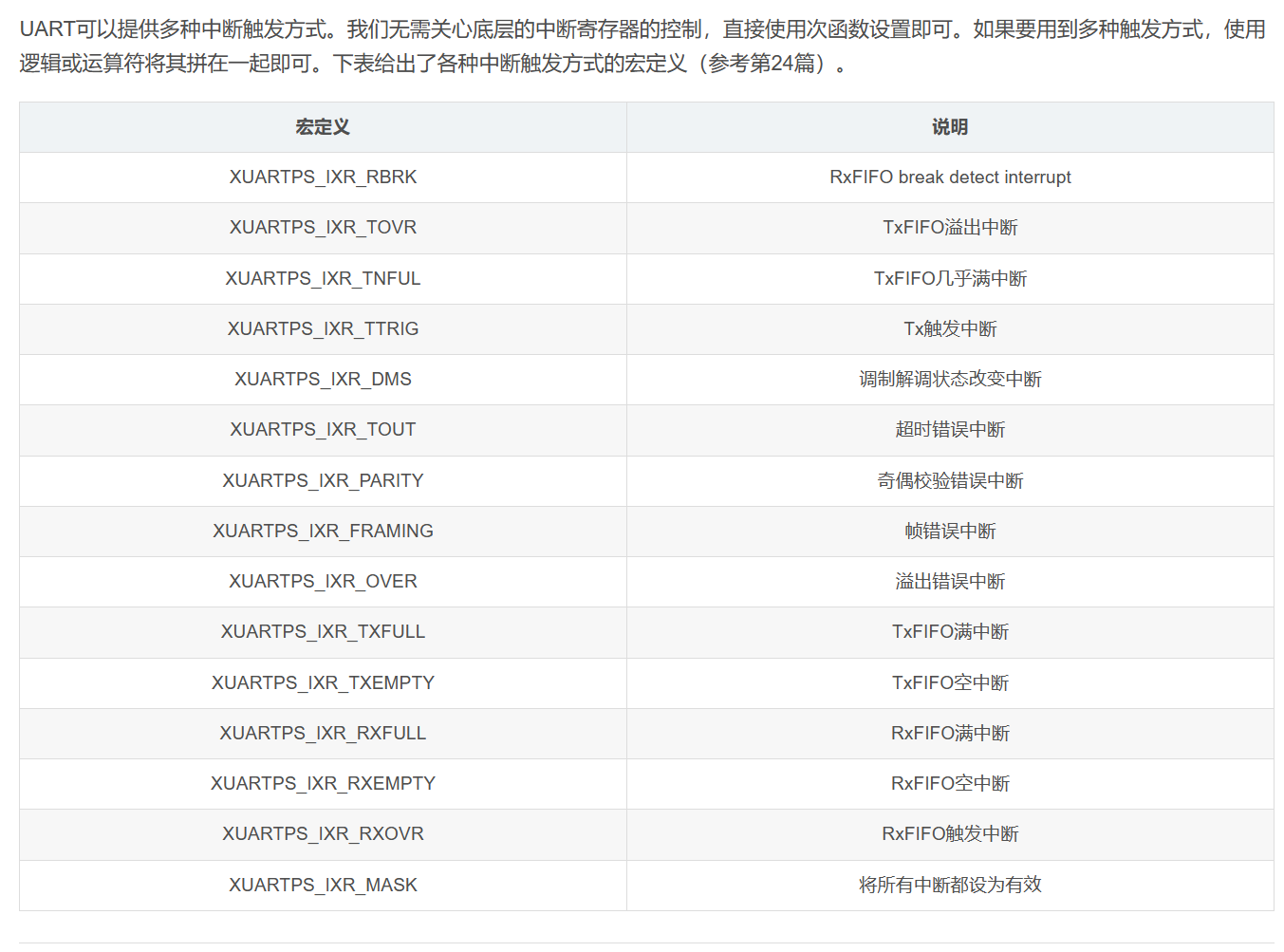
中断:Zynq Uart中断的流程和例程~UG585的CH.19
Zynq里的uart UART 控制器是全双工异步接收器和发送器,支持多种可编程波特率和 I/O 信号格式。该控制器可以适应自动奇偶校验生成和多主机检测模式。 UART 操作由配置和模式寄存器控制。使用状态、中断状态和调制解调器状态寄存器读取 FIFO、调制解调器信号…...

计算机补码能够减法转加法的原因
...
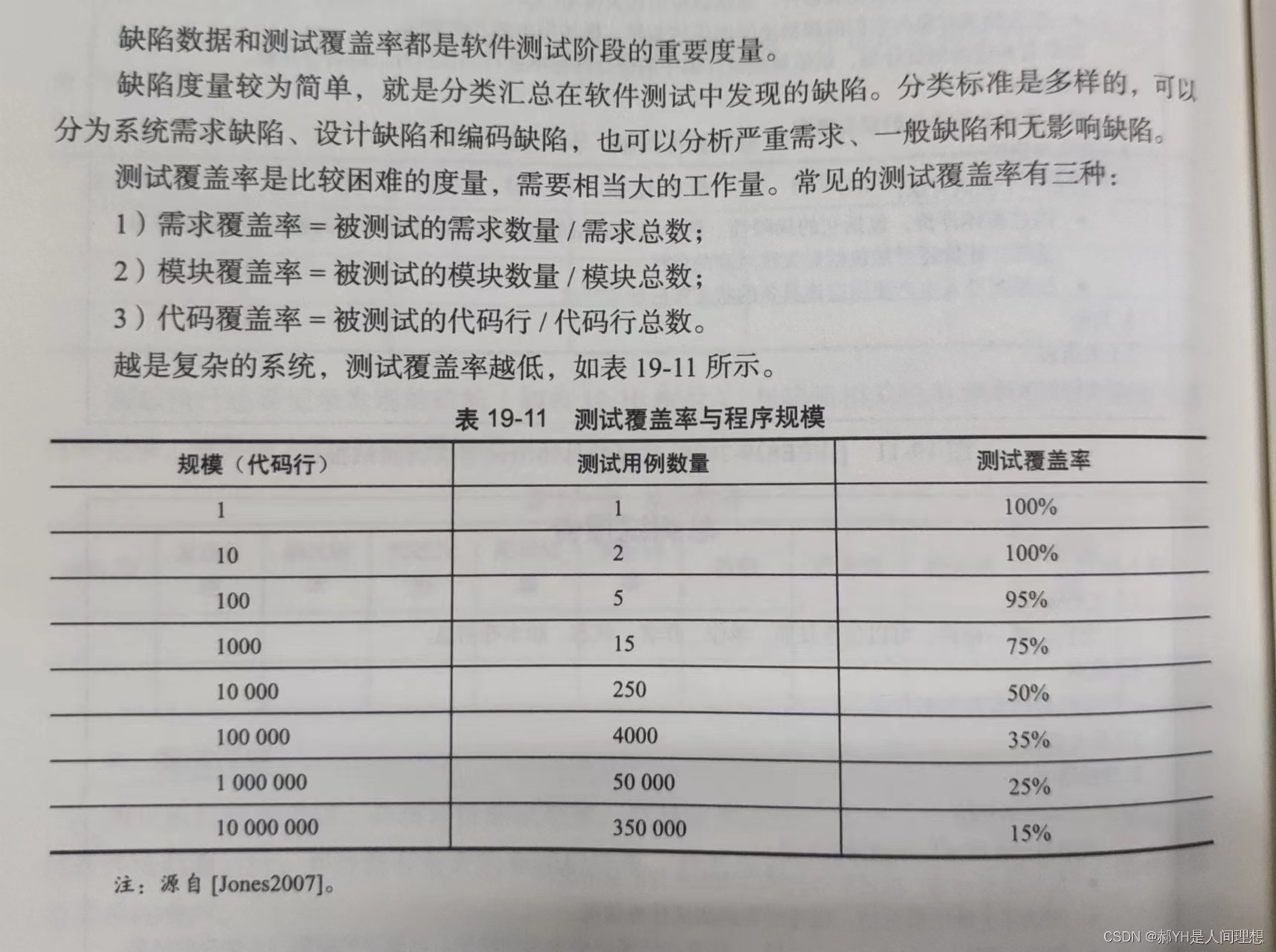
软件工程与计算总结(十九)软件测试
目录 编辑 一.引言 1.验证与确认 2.目标 3.测试用例 4.桩与驱动 5.缺陷、错误与失败 二.测试层次 1.测试层次的划分 2.单元测试 3.集成测试 4.系统测试 三.测试技术 1.测试用例的选择 2.随机测试 3.基于规格的技术(黑盒测试) 4.基于代…...

Tomcat设置IP黑名单和白名单server.xml
方式一: -- 只允许192.168.1.2和192.168.2.3 <Context path"" docBase"xxxAdmin" debug"0" reloadable"true" ><Valve className"org.apache.catalina.valves.RemoteAddrValve" allow"192.168.1.…...

【AI视野·今日NLP 自然语言处理论文速览 第五十五期】Mon, 16 Oct 2023
AI视野今日CS.NLP 自然语言处理论文速览 Mon, 16 Oct 2023 Totally 53 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers PromptRE: Weakly-Supervised Document-Level Relation Extraction via Prompting-Based Data Programming Au…...

k8s crd设置额外header
可以通过设置crd.spec.additionalPrinterColumns来实现: apiVersion: apiextensions.k8s.io/v1 kind: CustomResourceDefinition metadata:name: crontabs.stable.example.com spec:group: stable.example.comscope: Namespacednames:plural: crontabssingular: cr…...

电容笔好还是触屏笔好?便宜又好用的电容笔推荐
目前有哪些电容笔值得买?相比于之前的电容笔,现在的电容笔增加了很多新的特性功能,例如防误触、避免手指不小心触碰屏幕造成书写错误、笔画粗细可以自由调整等。苹果最初的Pencil现在售价一直高居不下。所以,如果你没有过多的预算…...

列表作为条件查询的参数
<if test"secucodeList ! null and secucodeList.size() > 0">...
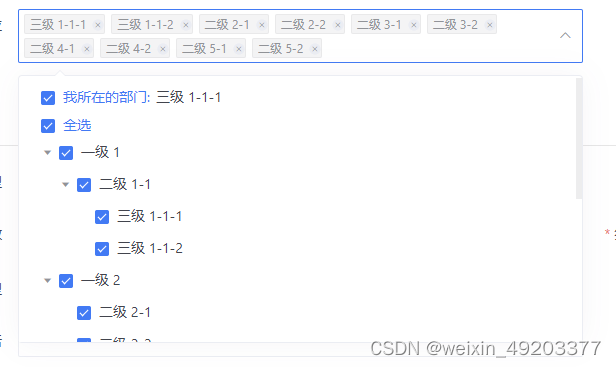
elementui中el-select和el-tree实现下拉树形多选功能
实现效果如下: 代码如下: html中 <el-col :lg"12"><el-form-item label"可用单位" prop"useOrgListTemp"><div class"departAll"><el-selectref"selectTree"v-model"valu…...

手机怎么监控电脑?
随着企业对电脑监控需求的增加,越来越多的管理者意识到使用电脑监控电脑的不便性,一旦外出就无法实时查看监控。其实可以用手机实现监控电脑的需求,只需在被监控端安装电脑监控软件后,将电脑设备和员工信息进行绑定,使…...
)
职场题:有一件特别紧急的事,群众要办理,且联系不上领导,你怎么办?(2)
接1所写 如果无法联系上领导且有一项特别紧急的事情需要办理,以下是进一步的建议: 11. 尝试其他沟通渠道:除了直接联系领导外,尝试通过其他沟通渠道与领导取得联系。这可能包括电子邮件、即时通讯工具或其他内部通信平台。确保详…...

《深入理解java虚拟机 第三版》学习笔记一
第 2 章 Java 内存区域与内存溢出异常 2.2 运行时数据区域 Java 虚拟机在执行 Java 程序的过程中会把它所管理的内存划分为若干个不同的数据区域。这些区域有各自的用途,以及创建和销毁的时间,有的区域随着虚拟机进程的启动而一直存在,有些…...

webGL编程指南 第三章 旋转三角形
我会持续更新关于wegl的编程指南中的代码。 当前的代码不会使用书中的缩写,每一步都是会展开写。希望能给后来学习的一些帮助 git代码地址 接着 上一节 接着做平移的转化。本案例是三角形的旋转 <!DOCTYPE html> <html lang"en"><head…...

网络安全是什么?一文认识网络安全
一、网络安全 1.概念 网络安全从其本质上讲就是网络上的信息安全,指网络系统的硬件、软件及数据受到保护。不遭受破坏、更改、泄露,系统可靠正常地运行,网络服务不中断。 (1)基本特征 网络安全根据其本质的界定&#…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
