动态规划解股票类型
文章目录
- 单只股票买卖
- 多次买卖单只股票
- 最多两次买卖股票
- 最多买k次
- 含冷静期
- 含手续费
单只股票买卖
买卖股票的最佳时机
关键思路:找到一个值,他与之后的最大值之差最大。
用minprice记录最小的值,用maxprofit记录最大的收益。
想清楚一个点:
- 更新最小值时,影响最大收益吗?
- 不会影响,因为每个收益都是需要根据minprice后续的最大值
class Solution {public int maxProfit(int[] prices) {if(prices.length<=1) return 0;int n = prices.length;int minprice = Integer.MAX_VALUE;int maxprofit = 0;for(int i = 0 ; i < n ;i++ ){minprice =Math.min(minprice, prices[i]);maxprofit = Math.max(prices[i] -minprice,maxprofit);}return maxprofit;}
}
多次买卖单只股票
买卖股票的最佳时机 II
profitBuy 用于记录已购买股票后的最大利润,而 profitNOBuy 用于记录未购买股票时的最大利润。在一个循环中,它逐步计算了每一天的最佳策略,然后返回最后一天的最大利润。
profitBuy[i]表示在第i天持有股票时的最大利润,它等于在第i-1天继续持有股票或在第i-1天卖出股票后买入的最大值。profitNOBuy[i]表示在第i天没有持有股票时的最大利润,它等于在第i-1天继续观望不购买股票或在第i-1天购买股票后卖出的最大值。
在遍历结束后,函数返回两种情况的最大值,即最大利润。用动态规划的方法来解决买卖股票的问题,确保在每一天都选择最优的策略以获得最大的利润。
class Solution {public int maxProfit(int[] prices) {int n = prices.length;int profitBuy[] = new int[n]; // 用于记录已购买股票后的最大利润int profitNOBuy[] = new int[n]; // 用于记录未购买股票时的最大利润profitBuy[0] = -prices[0]; // 初始化第一天已购买的情况,初始资金为负的第一天股票价格profitNOBuy[0] = 0; // 初始化第一天未购买股票的情况,初始资金为0for (int i = 1; i < n; i++) {// 更新已购买股票后的最大利润,考虑继续持有或卖出的情况profitBuy[i] = Math.max(profitBuy[i - 1], profitNOBuy[i - 1] - prices[i]);// 更新未购买股票时的最大利润,考虑继续观望或购买的情况profitNOBuy[i] = Math.max(profitNOBuy[i - 1], profitBuy[i - 1] + prices[i]);}// 最终返回最后一天的两种情况的最大值,即最大利润return Math.max(profitBuy[n - 1], profitNOBuy[n - 1]);}
}最多两次买卖股票
123. 买卖股票的最佳时机 III
- 首先,定义了四个变量:
minprice,maxprofit,minprice2,和maxprofit2,它们用来存储在遍历价格数组过程中的一些重要信息。 - 通过循环遍历价格数组
prices,其中i表示当前的天数。 minprice用来记录在第i天之前的最低股票价格。在循循环过程中,不断更新minprice为当前价格prices[i]和minprice之间的较小值。maxprofit用来记录在第i天卖出股票时的最大利润。利润计算为当前价格prices[i]减去之前的最低价格minprice,并且与之前的最大利润maxprofit比较,取较大值。minprice2用来记录在第i天之前的最低股票价格,考虑到第二次交易。这里minprice2考虑了第一次交易的收益maxprofit,即prices[i] - maxprofit,因为在第一次交易中,你已经卖出了一次股票,所以要减去第一次交易的利润。maxprofit2用来记录在第i天卖出股票时的最大利润,考虑第二次交易。利润计算为当前价格prices[i]减去之前的最低价格minprice2,并与之前的最大利润maxprofit2比较,取较大值。- 最后,返回
Math.max(maxprofit2, maxprofit),因为你要最大化两次交易的总利润。
这个算法的关键在于动态地维护四个变量,以确保在每一天都考虑了两次交易的情况,并计算出最大利润。
class Solution {public int maxProfit(int[] prices) {int n = prices.length;if(n<=1) return 0;int minprice = Integer.MAX_VALUE;int maxprofit = 0;int minprice2 = Integer.MAX_VALUE;int maxprofit2 = 0;for(int i = 0 ; i < n ;i++ ){minprice = Math.min(minprice, prices[i]);minprice2 = Math.min(minprice2 , prices[i] - maxprofit);maxprofit = Math.max(prices[i] -minprice,maxprofit);maxprofit2 = Math.max(maxprofit2 , prices[i] - minprice2);}return Math.max(maxprofit2,maxprofit);}
}
最多买k次
188. 买卖股票的最佳时机 IV
把k想象成2即可,按照两次的思路
class Solution {public int maxProfit(int k, int[] prices) {int n = prices.length;if(n<=1) return 0;int minprice[] = new int[k];int maxprofit[] = new int[k];for(int i=0;i<k;i++){minprice[i] = Integer.MAX_VALUE;maxprofit[i] = 0;}for(int i = 0 ; i < n ;i++ ){minprice[0] = Math.min(minprice[0], prices[i]);maxprofit[0] = Math.max(prices[i] -minprice[0],maxprofit[0]); for(int j=1;j<k;j++){minprice[j] = Math.min(minprice[j] , prices[i] - maxprofit[j-1]); maxprofit[j] = Math.max(maxprofit[j] , prices[i] - minprice[j]);}}return maxprofit[k-1];}
}
含冷静期
309. 买卖股票的最佳时机含冷冻期
状态转移图
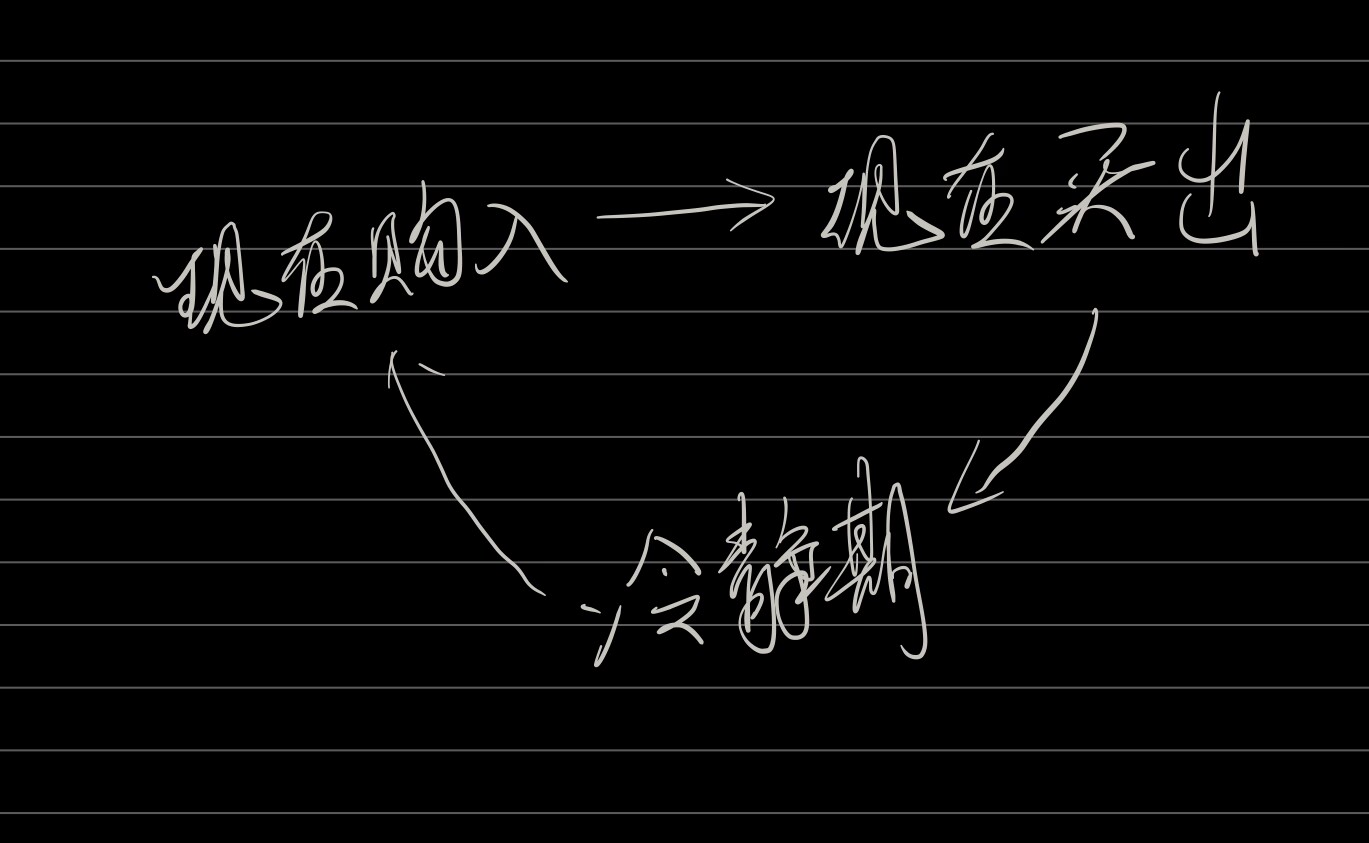
class Solution {public int maxProfit(int[] prices) {int n = prices.length;if(n<=1) return 0;int dpNoBuy[] = new int[n];int dpBuy[] = new int[n];int dpCd[] = new int[n];dpNoBuy[0] = -prices[0];dpBuy[0] = 0;dpCd[0] = 0;for (int i = 1; i < n; i ++) {dpNoBuy[i] = Math.max(dpCd[i-1] - prices[i],dpNoBuy[i-1]);dpBuy[i] = Math.max(dpNoBuy[i-1] + prices[i],dpBuy[i-1]);dpCd[i] = Math.max(dpCd[i-1],dpBuy[i-1]);}return Math.max(Math.max(dpNoBuy[n-1],dpCd[n-1]),dpBuy[n-1]);}
}
含手续费
714. 买卖股票的最佳时机含手续费
两个状态转换即可
class Solution {public int maxProfit(int[] prices, int fee) {int n = prices.length;if(n<=1) return 0;int buy[] = new int[n];int sell[] = new int[n];buy[0] = -prices[0];sell[0] = 0;for(int i = 1;i<n;i++){buy[i] = Math.max(buy[i-1],sell[i-1]-prices[i]);sell[i] = Math.max(sell[i-1],buy[i]+prices[i]-fee);}return Math.max(buy[n-1],sell[n-1]);}
}
相关文章:

动态规划解股票类型
文章目录 单只股票买卖多次买卖单只股票最多两次买卖股票最多买k次含冷静期含手续费 单只股票买卖 买卖股票的最佳时机 关键思路:找到一个值,他与之后的最大值之差最大。 用minprice记录最小的值,用maxprofit记录最大的收益。 想清楚一个点…...

前端用 js-file-download组件下载后端返回的pdf,word,excel文件
后端返回的pdf,word,excel的文件流导出需要让浏览器下载文件 1、安装js-file-download组件 npm install js-file-download --save 2、在对应的页面引用 import fileDownload from "js-file-download"; 3、在接口返回结果后直接调用即可 let data{id:processId,c…...
Mac硬盘检测工具
Mac硬盘检测软件是一款用于检测和诊断Mac硬盘健康状态的工具,帮助用户及时发现潜在的硬盘问题,避免数据丢失和系统故障。通过全面的检测和报告功能,用户可以更好地了解自己的硬盘状况,确保数据的安全和可靠。给大家介绍几款好用的…...
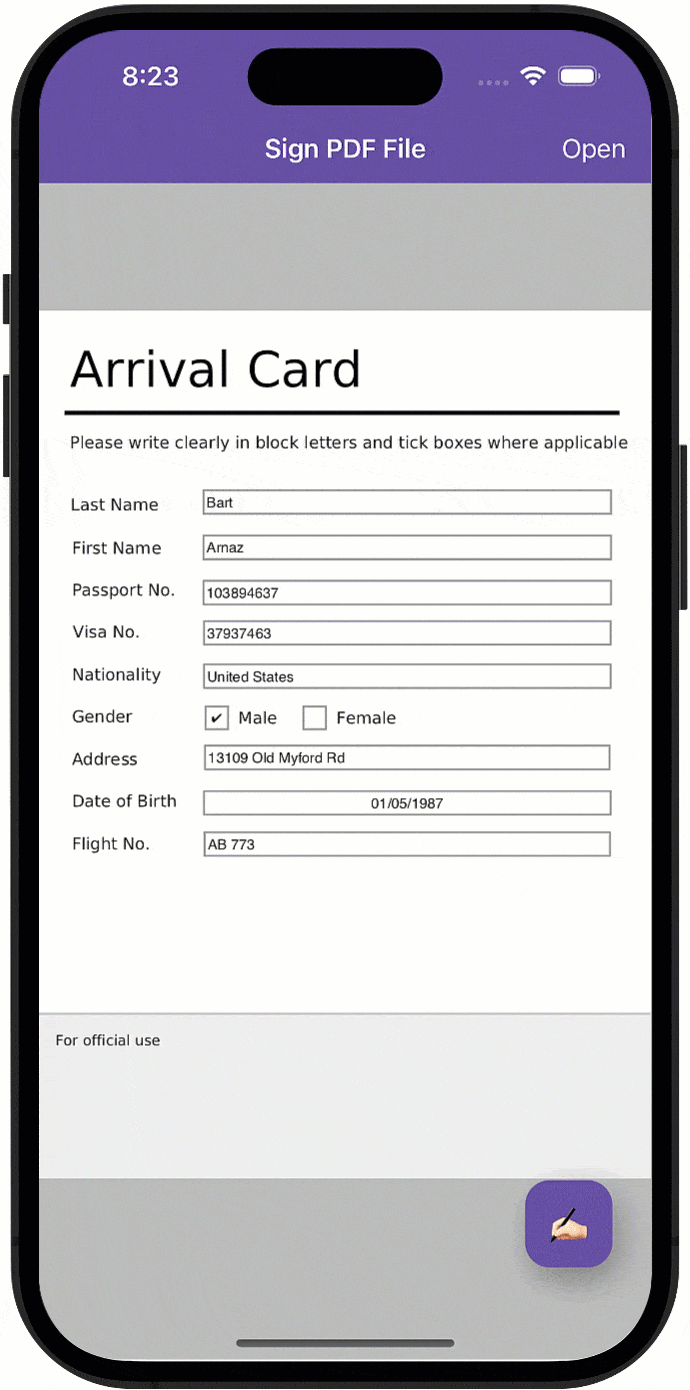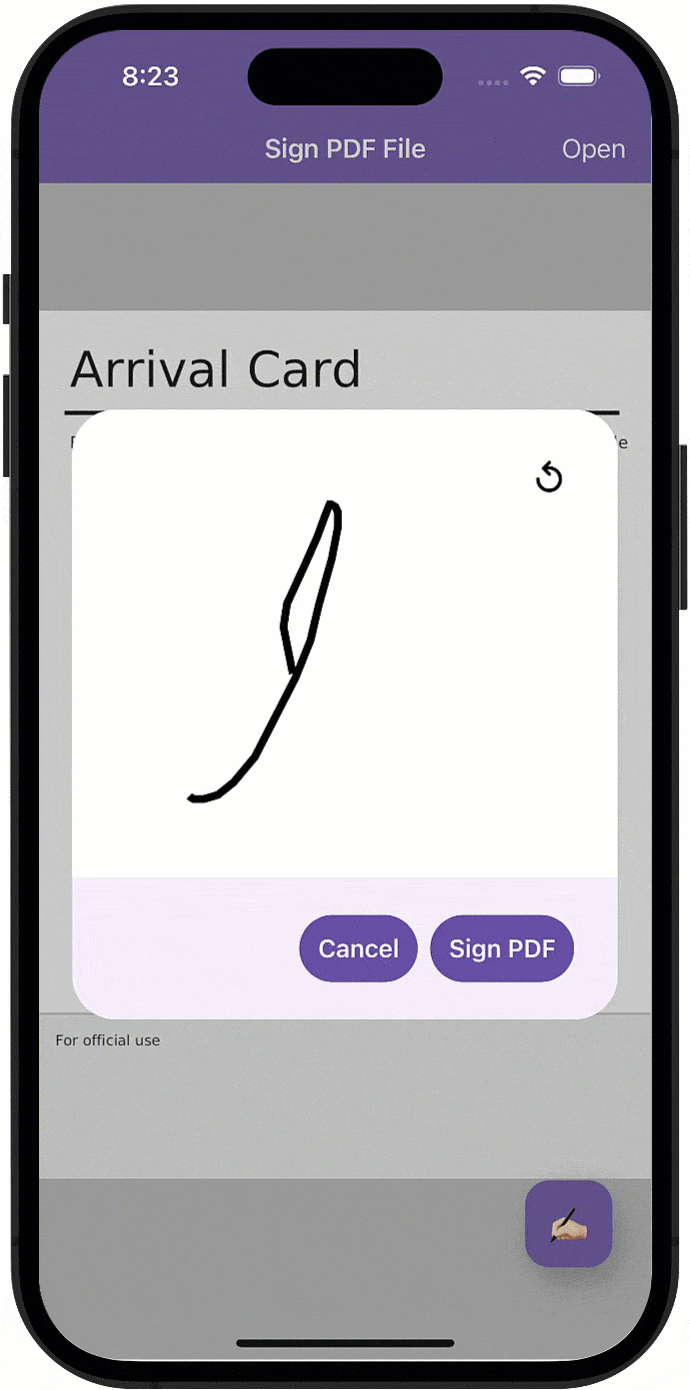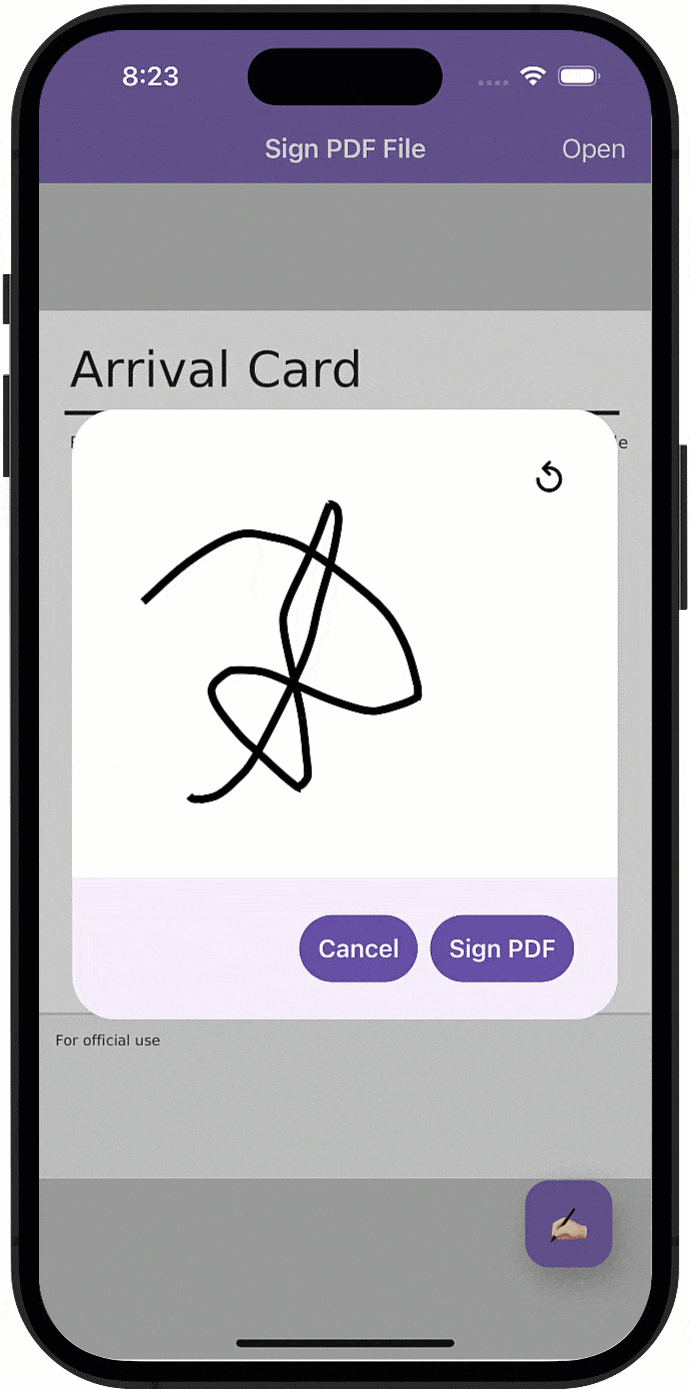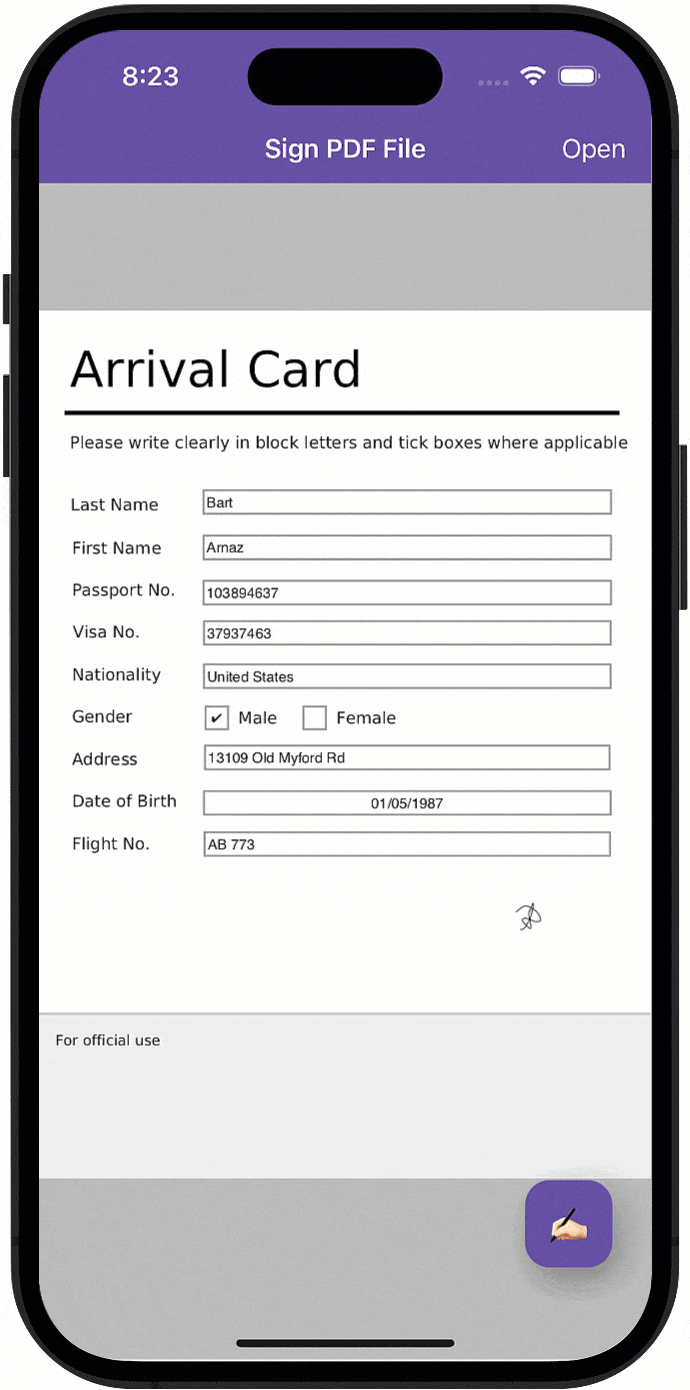
一篇文章解密如何轻松实现移动应用的电子和手绘PDF签名功能!
对PDF文件签名是移动设备上越来越普遍的使用需求,本文将描述自动生成/“手绘”签名与如何使用DevExpress Office File API组件来实现在.NET MAUI应用程序中快速合并签名/签名支持之间的区别。 DevExpress Office File API是一个专为C#, VB.NET 和 ASP.NET等开发人员…...

【大数据】Kafka 入门简介
Kafka 入门简介 1.什么是 Kafka2.Kafka 的基本概念3.Kafka 分布式架构4.配置单机版 Kafka4.1 下载并解压包4.2 启动 Kafka4.3 创建 Topic4.4 向 Topic 中发送消息4.5 从 Topic 中消费消息 5.实验5.1 实验一:Python 实现生产者消费者5.2 实验二:消费组实现…...

Unity可视化Shader工具ASE介绍——8、UI类型的特效Shader编写
阿赵的Unity可视化Shader工具ASE介绍目录 Unity的UGUI图片特效角色闪卡效果 大家好,我是阿赵。 继续介绍Unity可视化Shader编辑插件ASE的使用。这次讲一下UI类特效Shader的写法。 一、例子说明 这次编写一个Shader,给一张UGUI里面的图片增加一个闪卡…...

科学指南针XPS | SEM | BET 降价:不赚钱,就和您交个朋友
尊敬的各位客户: 感谢您一直以来对科学指南针服务平台(下文简称:科学指南针)的支持和信任!科学指南针本着服务第一,客户至上的精神,多年来坚持为客户提供高质量的测试和服务,获得了广…...
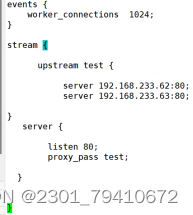
nginx正反向代理,负载均衡
Nginx 正向代理,反向代理 ,负载均衡 Nginx有两种代理协议 七层代理(http协议) 四层代理(tcp/udp流量转发) 四层代理七层代理概念 四层代理 四层代理:基于tcp/ip协议层的转发代理方式&#…...
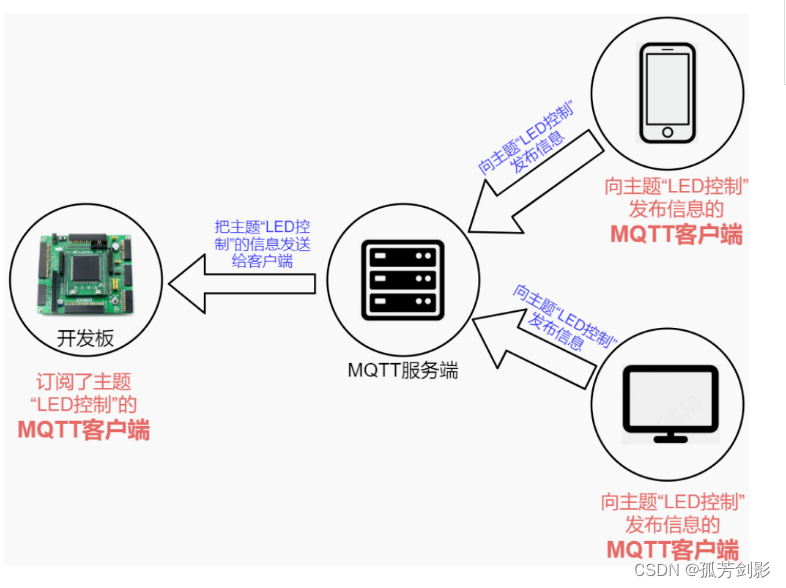
物联网中的MQTT协议总结
本文引注: https://mp.weixin.qq.com/s/y55wqYoWEvU9Q3-I0uu3cg 物联网曾被认为是继计算机、互联网之后,信息技术行业的第三次浪潮。随着基础通讯设施的不断完善,尤其是 5G 的出现,进一步降低了万物互联的门槛和成本。物联网本身也是 AI 和区…...

断点续传的原理和实现
断点续传是一种文件上传或下载的技术,允许用户在上传或下载中断后恢复操作而不必重新开始。其原理和实现可以分为以下步骤: 原理: 文件分割:将大文件分割成小块(分片)。上传/下载:客户端上传或…...
【小黑嵌入式系统第二课】嵌入式系统的概述(二)——外围设备、处理器、ARM、操作系统
上一课: 【小黑嵌入式系统第一课】嵌入式系统的概述(一)——概念、特点、发展、应用 下一课: 【小黑嵌入式系统第三课】嵌入式系统硬件平台(一)——概述、总线、存储设备(RAM&ROM&FLASH…...

Unity3D 在做性能优化时怎么准确判断是内存、CPU、GPU瓶颈详解
Unity3D是一款广泛应用于游戏开发的跨平台游戏引擎,但在开发过程中,我们经常会遇到性能瓶颈问题,如内存、CPU和GPU瓶颈。本文将详细介绍在Unity3D中如何准确判断和解决这些瓶颈问题,并给出相应的技术详解和代码实现。 对惹&#…...
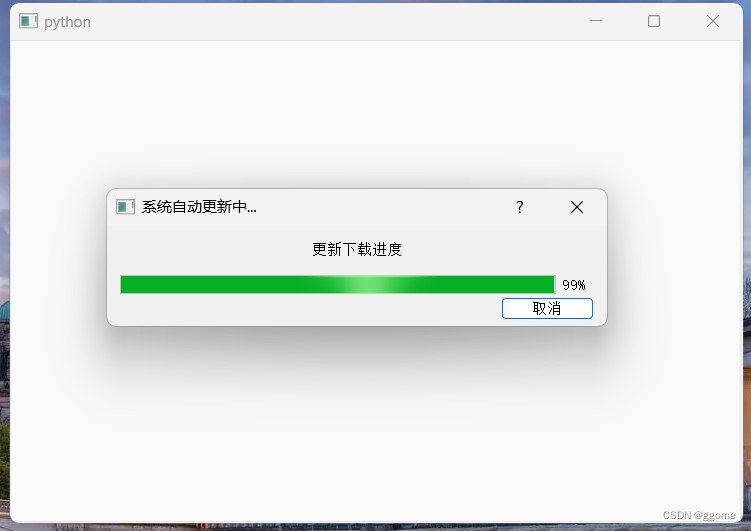
pyqt5 QProgressDialog 进度条的使用 下载自动更新应用程序
pyqt5 QProgressDialog 进度条的使用 案例截图 思路 实例化进度条窗口设置窗口各属性包括标题 提示文字 和 窗口大小显示进度条窗口同过一个for循环 模拟进度 代码 from PyQt5.QtCore import QCoreApplication, QProcess from PyQt5.QtWidgets import QApplication,QProgre…...

【yolov5目标检测】使用yolov5训练自己的训练集
数据集准备 首先得准备好数据集,你的数据集至少包含images和labels,严格来说你的images应该包含训练集train、验证集val和测试集test,不过为了简单说明使用步骤,其中test可以不要,val和train可以用同一个,…...

出差学小白知识No5:ubuntu连接开发板|上传源码包|板端运行的环境部署
1、ubuntu连接开发板: 在ubuntu终端通过ssh协议来连接开发板,例如: ssh root<IP_address> 即可 这篇文章中也有关于如何连接开发板的介绍,可以参考SOC侧跨域实现DDS通信总结 2、源码包上传 通过scp指令,在ub…...

C++(初阶四)类和对象
文章目录 一、面向过程和面向对象初步认识二、类的引入三、类的定义1、类的概述2、类的两种定义3、成员变量命名规则的建议 四、类的访问限定符及封装1、访问限定符2、封装 五、类的作用域六、类的实例化七、类对象模型1、如何计算类对象的大小2、 类对象的存储方式猜测3、 验证…...

CSS餐厅练习链接及答案
目录 链接: level 1 level 2 level 3 level 4 level 5 level 6 level 7 level 8 level 9 level 10 level 11 level 12 level 13 level 14 level 15 level 16 level 17 level 18 level 19 level 20 level 21 level 22 level 23 level 24 le…...
嵌入式和 Java选哪个?
今日话题,嵌入式和 Java 走哪个?对于嵌入式领域有浓厚兴趣的人,并不会比Java行业薪资低,处于上中游水平。特别是从2020年开始,嵌入式领域受益于芯片产业的兴起,表现出了强劲的增长势头。薪资水平受多方面因素影响。以…...
)
创建带Axi_Lite接口的IP核与AXI Interconnect(PG059)
AXI Interconnect互连内核将一个或多个 AXI 内存映射主设备连接到一个或多个内存映射从设备。 参考小梅哥文档。 /**************************** 类型定义 ****************** **********/ /** * * 将值写入 AXI_REG_LIST 寄存器。执行 32 位写入。 * 如果组件以较小的宽度实…...
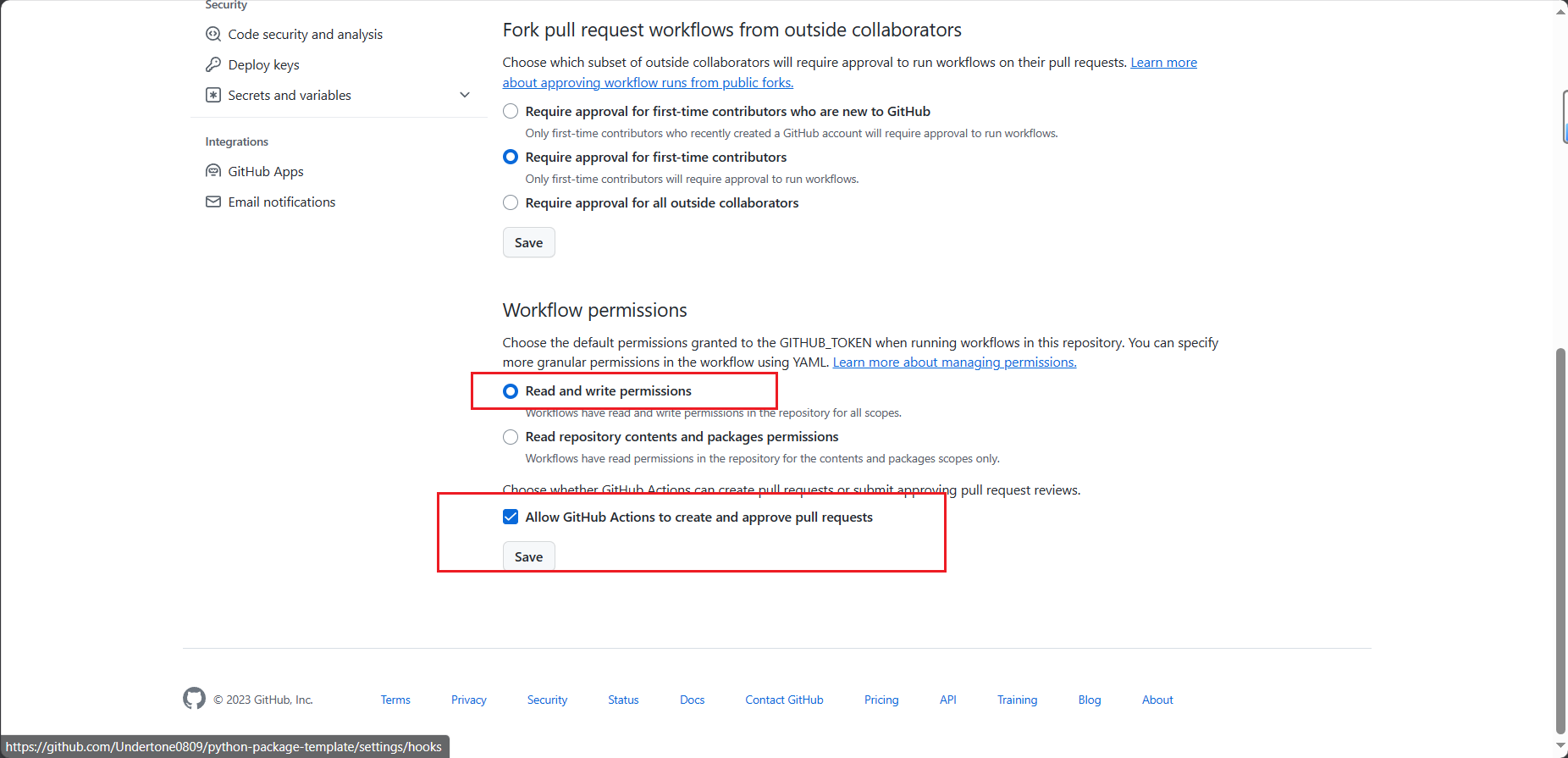
快速解决 Resource not accessible by integration
简介 最近好久没有写博客了,今天在写开源项目 python-package-template 的时候,正好遇到一个问题,记录一下吧。本文将介绍 Resource not accessible by integration 的几种解决方案。 也欢迎大家体验一下 python-package-template 这个项目&…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
