Python 机器学习入门之K-Means聚类算法
系列文章目录
第一章 Python 机器学习入门之线性回归
K-Means聚类算法
- 系列文章目录
- 前言
- 一、K-Means简介
- 1、定义
- 2、例子
- 3、K-Means与KNN
- 二、 K-Means实现
- 1、步骤
- 2、优化
- 2.1 初始化优化之K-Means++
- 2.2 距离优化之elkan K-Means
- 三、优缺点
- 1、优点
- 2、缺点
前言
学完K近邻算法,让我们再来看看和它有一定相似程度的K-Means聚类算法
一、K-Means简介
1、定义
wiki定义:
k-均值算法(英文:k-means clustering)源于信号处理中的一种向量量化方法,现在则更多地作为一种聚类分析方法流行于数据挖掘领域。k-均值聚类的目的是:把n个点(可以是样本的一次观察或一个实例)划分到k个聚类中,使得每个点都属于离他最近的均值(此即聚类中心)对应的聚类,以之作为聚类的标准。
这里说下聚类和簇的概念,使用上述算法会把训练中的数据划分成若干个组,每个组就被称为簇,而这种学习方式或者说分类过程就被称为聚类;但是很多资料上往往也会把聚类视作簇,就如上述定义一样。
2、例子
简单来说,K聚类的核心点是找到K个中心点,以此为中心辐射开来,形成K个簇;
举个例子,有些大学在入学时会让学生填写一些个人作息和兴趣爱好来做宿舍分配,其中就可以使用K-Means聚类算法,假设要分配K个宿舍,我们可以先随机出K个学生,然后在此基础上分配剩下的学生,剩下的学生找到与自己个人作息和兴趣爱好相近的K个学生之一;最后我们就可以得到一个相对较好的宿舍环境,熬夜打游戏的可以一起组团开黑,早起学习的可以一起携手前去图书馆,大家都获得了美好的未来。

3、K-Means与KNN
前言里提到K-Means和KNN有一定相似程度,这是因为二者在运行过程中都用到了最近邻思想,都是找到离某个点最近的点;但是它们不能统一而论,这是它们的区别点
- KNN是有监督学习,是有对应的类别输出的;K-Means是无监督学习,没有样本输出
- KNN是找离当前点最近的K个点,K-Means是找离当前点最近的K个中心点之一
二、 K-Means实现
1、步骤
-
选取初始化的k个样本设为聚类中心a=a1,a2,a3…ak;
-
对于数据集的每个数据点Xi,计算它到k个聚类中心的距离(这里通常采用我们在上一篇k近邻中提到的欧式距离来计算),然后将它分到距离最小的聚类中心所对应的簇中;
-
针对每个聚类中心aj,当有新的样本加入时,重新计算它的质心(中心点)
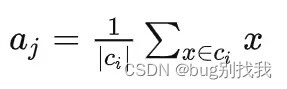
-
重复上述2、3步直至达到终止条件
2、优化
2.1 初始化优化之K-Means++
传统K-Means是随机选择中心点,这样有很大概率会花费更多的时间,因此在选择初始点上我们可以使用更好的方法,那就是K-Means++;
相比于传统K-Means,K-Means在选择新的初始点时都会参考之前选取得初始点,因为我们知道最后得出的结果是K个簇,我们希望每个簇之间的距离越远越好,而这点就可以应用到初始点选择上,我们在选择新的初始点希望找到离之前的初始点越远越好;
步骤:
- 随机选择一个初始点a1
- 对于数据集中每一个点Xi,计算它到之前每个聚类中心aj的距离D(xi),找到距离最大的那个,但是这只适用于单个距离中心的情况;当面对多个聚类中心,我们使用概率的方式(下式)来找到最可能距离前j个聚类中心最远的点
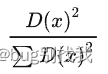
- 重复第二步直至找到K个聚类中心
2.2 距离优化之elkan K-Means
传统K-Means中,每次迭代都需要计算机所有样本到所有质心的位置,这样运行时间过长;elkan K-Means算法则是对这一步进行改进,减少不必要的距离的计算;它主要的使用的思想是:利用两边之和大于等于第三边,两边之差小于第三边的三角形的性质,因此达到减少距离计算的目的。
- 对于一个样本点x和两个质心a1,a2;我们先计算出这两个质心的距离D(a1,a2),如果2D(a1,x)<=D(a1,a2),那么D(a2,x)>=D(a1,x),就可以不计算D(a2,x),减少一步计算距离
- 对于一个样本点x和两个质心a1,a2,我们可以得到D(a2,x)>=max(0,D(a1,x)-D(a1,a2))
第二条规律其实有点难懂,我查阅了下资料,大概是说利用两边之差小于第三边推导出来,然后在此基础上来利用该公式能判断是否可以不用计算D(a2,x)
该方法可以一定程度上提升传统K-Means聚类算法的迭代速度,但是如果样本的特征是稀疏的,并具有缺失值,由于有些距离无法计算,则无法使用该算法。
三、优缺点
1、优点
- 简单易懂,算法收敛速度快
- 算法的可解释性强
2、缺点
- k值的选取一般需要先验经验(专家经验)
- 采用迭代的方法,得到的结果只是局部最优
- 由于需要计算质心到所有点的距离,对噪音和异常点比较敏感
- 如果各隐含类别的数据量严重失衡,或者个各隐含类别的方差不同,则聚类效果不佳
相关文章:
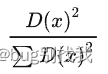
Python 机器学习入门之K-Means聚类算法
系列文章目录 第一章 Python 机器学习入门之线性回归 K-Means聚类算法 系列文章目录前言一、K-Means简介1、定义2、例子3、K-Means与KNN 二、 K-Means实现1、步骤2、优化2.1 初始化优化之K-Means2.2 距离优化之elkan K-Means 三、优缺点1、优点2、缺点 前言 学完K近邻算法&a…...
【jmeter】接口测试流程
1、Jmeter简介 Jmeter是由Apache公司开发的一个纯Java的开源项目,即可以用于做接口测试也可以用于做性能测试。 Jmeter具备高移植性,可以实现跨平台运行。 Jmeter可以实现分布式负载。 Jmeter采用多线程,允许通过多个线程并发取样或通过独…...

RTOS(6)任务管理
任务状态理论 我们是怎么实现,两个同优先级的任务之间交替执行的呢? 任务切换的基础:tick中断! tick为1ms一个周期,可以通过修改时钟配置修改; running:正在进行的任务3为runningÿ…...

【UE5】 ListView使用DataTable数据的蓝图方法
【UE5】 ListView使用DataTable数据的蓝图方法 ListView 是虚幻引擎中的一种用户界面控件,用于显示可滚动的列表。它可以用于显示大量的数据,并提供了各种功能和自定义选项来满足不同的需求。 DataTable是虚幻引擎中的一种数据表格结构,用于存…...

Anthropic全球上线AI语言模型Claude 2;多模态系统:融合文本和图像的新前沿
🦉 AI新闻 🚀 Anthropic全球上线AI语言模型Claude 2,编程、数学、推理能力大幅提升 摘要:Anthropic在全球正式上线了AI语言模型Claude 2。相比前代版本,Claude 2在编程、数学、推理等方面都有大幅提升,支…...
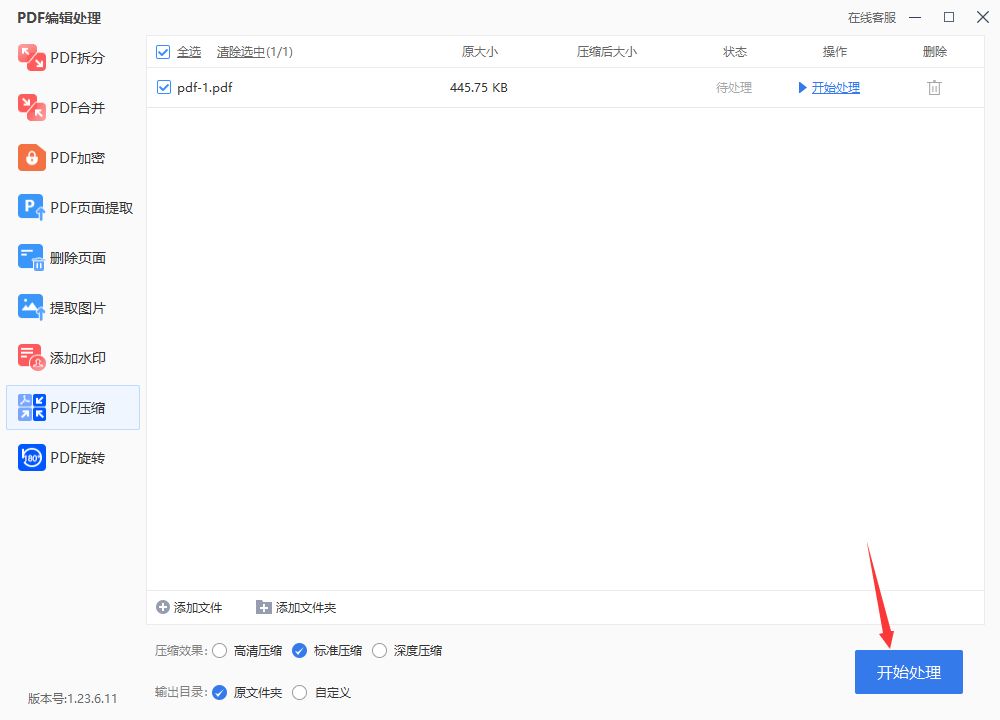
pdf压缩文件怎么压缩最小?
pdf压缩文件怎么压缩最小?我们很多项目介绍或是学术的报告都是采用的这个pdf格式,那么我们在存储或是需要进行分享的时候,可能就会因为文件过大而导致无法打开或是发送了。那么就需要将其进行压缩。PDF文件压缩方法很多,pdf压缩文…...

开源智能体来啦!港大团队发布OpenAgents,可以搞数据分析、聊天、支持200+插件
夕小瑶科技说 原创 作者 | 智商掉了一地、ZenMoore 港大的研究团队最近发布了一个新的开源 Agent 框架,名为 OpenAgents. 它可以用于实际用户场景,特别是在使用自然语言执行复杂任务的情况下。先前的语言智能体框架主要关注概念验证或者供开发人员使用&…...
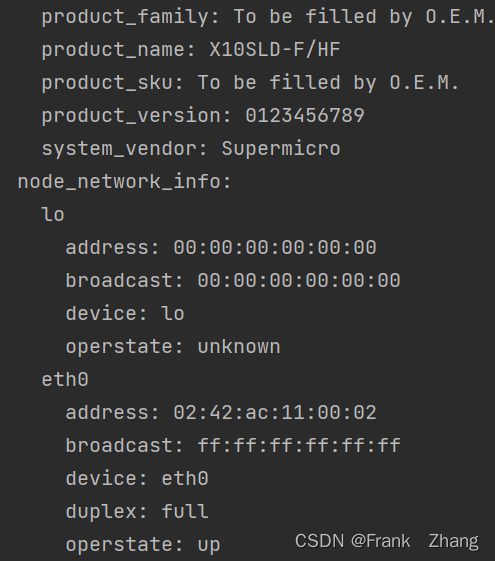
Prometheus metrics数据抓取解析
Prometheus node的监控数据如链接展示,我们希望能更加方便的看到监控数据,shodan对Prometheus metrics 的数据做了格式化处理。172.96.3.215:9100/metricshttp://172.96.3.215:9100/metrics 本文我自己实现了一个命令行工具,可以输出类shodan…...

【算法训练-排序算法 三】【排序应用】合并区间
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【合并区间】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...

【iOS】计算器仿写
文章目录 前言一、构建View界面二、Model中进行数据处理三、Controller层实现View与Model交互总结 前言 在前两周组内进行了计算器的仿写,计算器仿写主要用到了MVC框架的思想以及数据结构中用栈进行四则运算的思想,还有就是对OC中的字符串进行各种判错操…...

华为认证 | 华为HCIE认证该怎样备考?
华为HCIE认证是华为认证的最高级别,拥有了华为HCIE认证就代表拥有了华为官方认可的专家级技术水平。 因此HCIE认证的考试难度是非常高的,备考华为认证HCIE需要一定的准备和规划。 整理了一些简单易懂的指南,希望对各位备考的小伙伴一些帮助…...
10月份stable diffusion animatediff等插件使用指南,又来更新了
插件一直会更新,包含了基本市面上流行的90%插件,好用的插件更是不会错过,往期插件请看往期文章,如果你没有时间一直关注sd更新的进展,请关注我,一个月用几个小时看一下我的文章,最短时间跟进sd。…...
抓包工具charles修改请求和返回数据
数据篡改的主要使用场景: (1)mock场景,mock入参和返回值参数,实现mock测试 (2)安全测试,对于支付金额等比较重要的字段,可以修改请求参数来进行安全测试 1.首先选择要…...
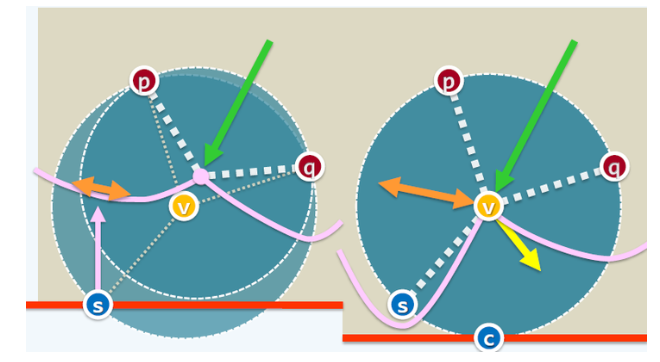
matlab中绘制 维诺图(Voronoi Diagram)
1.专业术语(相关概念): 基点Site:具有一些几何意义的点 细胞Cell:这个Cell中的任何一个点到Cell中基点中的距离都是最近的,离其他Site比离内部Site的距离都要远。 Cell的划分:基点Site与其它的…...

Mybatis TypeHandler 介绍及使用
Mybatis TypeHandler类型转换器是负责Java类和jdbc类型之间的转换 主要涉及到下面这几个类: TypeHandler 类型转换器的顶层接口BaseTypeHandler 抽象类继承自TypeHandler,Mybatis中所有的类型转换器实现均继承他。TypeHandlerRegistry 类型转换器注册器…...

Linux SVN 命令详解
1、将文件 checkout 到本地目录 svn checkout path(path是服务器上的目录) 例如:svn checkout svn://192.168.1.1/pro/domain 简写:svn co 2、往版本库中添加新的文件 svn add file 例如:svn add test.php(添加test.…...

Maven依赖引入的优先机制
xxxx待持续更新...
全开源无加密跨境电商购物网站系统源码(无货源模式+多语言+多货币)
在全球化的时代背景下,跨境电商成为了越来越受欢迎的消费方式,而建立一个源码无加密多语言跨境购物网站系统是一个具有挑战性的任务,但完全可行。以下是这个过程的一些主要步骤: 1. 确定需求和功能规划:先确定网站需要…...

Python常用视频编辑操作——读取与保存视频、更改帧数、拼接视频、视频语音合并、视频与图像互转等
1.更改视频帧数 降低视频帧数,简单的操作只能降低视频帧数,如果要增加视频帧数,那就要使用深度学习进行插帧处理: import cv2 from moviepy.editor import * def change_fps(inpt_path,output_path,fps):# 加载视频video Video…...

从javascript到vue再到react的演变
当提到前端开发中的框架时,JavaScript、Vue.js和React.js是三个最常见的名词。它们代表了Web开发中不同的技术选择和演变过程。本文将探讨JavaScript从原生到Vue.js再到React.js的演变,以及每个阶段的特点和优势。 JavaScript: 动态语言的基础 JavaScr…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
