LeetCode 2894. 分类求和并作差【数学,容斥原理】1140
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你两个正整数 n 和 m 。
现定义两个整数 num1 和 num2 ,如下所示:
num1:范围[1, n]内所有 无法被m整除 的整数之和。num2:范围[1, n]内所有 能够被m整除 的整数之和。
返回整数 num1 - num2 。
示例 1:
输入:n = 10, m = 3
输出:19
解释:在这个示例中:
- 范围 [1, 10] 内无法被 3 整除的整数为 [1,2,4,5,7,8,10] ,num1 = 这些整数之和 = 37 。
- 范围 [1, 10] 内能够被 3 整除的整数为 [3,6,9] ,num2 = 这些整数之和 = 18 。
返回 37 - 18 = 19 作为答案。
示例 2:
输入:n = 5, m = 6
输出:15
解释:在这个示例中:
- 范围 [1, 5] 内无法被 6 整除的整数为 [1,2,3,4,5] ,num1 = 这些整数之和 = 15 。
- 范围 [1, 5] 内能够被 6 整除的整数为 [] ,num2 = 这些整数之和 = 0 。
返回 15 - 0 = 15 作为答案。
示例 3:
输入:n = 5, m = 1
输出:-15
解释:在这个示例中:
- 范围 [1, 5] 内无法被 1 整除的整数为 [] ,num1 = 这些整数之和 = 0 。
- 范围 [1, 5] 内能够被 1 整除的整数为 [1,2,3,4,5] ,num2 = 这些整数之和 = 15 。
返回 0 - 15 = -15 作为答案。
提示:
1 <= n, m <= 1000
解法 容斥原理
设 k = ⌊ n m ⌋ k = \left\lfloor\dfrac{n}{m}\right\rfloor k=⌊mn⌋ 。 num 2 \textit{num}_2 num2 是 [ 1 , n ] [1,n] [1,n] 内的 m m m 的倍数之和,即
m + 2 m + ⋯ + k m = ( 1 + 2 + ⋯ + k ) ⋅ m = k ( k + 1 ) 2 ⋅ m \begin{aligned} &m + 2m + \cdots + km\\ =\ & (1+2+\cdots+k)\cdot m\\ =\ & \dfrac{k(k+1)}{2}\cdot m \end{aligned} = = m+2m+⋯+km(1+2+⋯+k)⋅m2k(k+1)⋅m
num 1 \textit{num}_1 num1 相当于 ( 1 + 2 + ⋯ + n ) − num 2 (1+2+\cdots+n) - \textit{num}_2 (1+2+⋯+n)−num2
所以
num 1 − num 2 = ( 1 + 2 + ⋯ + n ) − num 2 ⋅ 2 = n ( n + 1 ) 2 − k ( k + 1 ) m \begin{aligned} &\textit{num}_1 - \textit{num}_2\\ =\ & (1+2+\cdots+n) - \textit{num}_2 \cdot 2\\ =\ & \dfrac{n(n+1)}{2} - k(k+1)m \end{aligned} = = num1−num2(1+2+⋯+n)−num2⋅22n(n+1)−k(k+1)m
class Solution {
public:int differenceOfSums(int n, int m) {return n * (n + 1) / 2 - n / m * (n / m + 1) * m;}
};
复杂度分析:
- 时间复杂度: O ( 1 ) \mathcal{O}(1) O(1) 。
- 空间复杂度: O ( 1 ) \mathcal{O}(1) O(1) 。
相关文章:

LeetCode 2894. 分类求和并作差【数学,容斥原理】1140
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

100天掌握网络安全知识点!
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...

【ArcGIS绘图系列1】在ArcGIS中制作柱状图与饼状图
成图展示 图形出处:J2023-Assessment of agricultural drought based on multi-source remote sensing data in a major grain producing area of Northwest China 实现步骤 第一步 查看数据信息 数据输入到ArcGIS中:包含数据表和shp文件 1、shp文件…...

【c++】跟webrtc学std array 1: 混音的多维数组
对于固定大小的数组,非常适合用std的array 实现。静态赋初值 static constexpr std::array<int, 5> kInputValues = {0, 1, 2, 1, 0}...

App出海起量难?传参安装打开获客增长新途径
近年来,在App出海潮越发热烈的背景下,如何适应海外市场并实现“用户增长”与“提高转化”,已成为出海团队需要面临的重大挑战之一。 如何在海外市场短时间内快速起量?这个问题难倒了不少出海创业者,毕竟目前互联网环境…...

当AI遇上3D建模:一场创意与技术的完美碰撞!
在这个充满无限可能的时代,科技的发展日新月异,让我们见证了一场创意与技术的完美碰撞——AI与3D建模的结合。这种结合为我们开辟了一个全新的领域,让我们在虚拟世界中自由挥洒创意,为现实世界创造更多的可能性。 3D建模AI生成是…...

工作中的有效沟通
工作中的有效沟通 发现问题并解决问题发现问题解决问题 发现问题并解决问题 发现问题 清楚问题痛点。 注意与三方沟通时,一方沟通不明确时,则更需要想办法. 引导或者特别注意语句限制词汇,弄清楚意思。比如: 信息科要求5分钟无…...
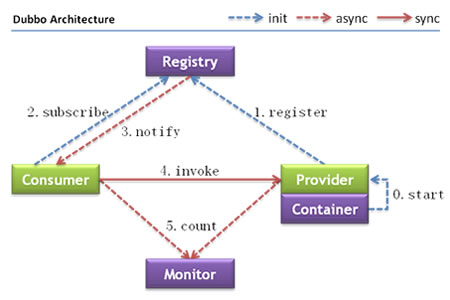
1.集合框架
一、JDK版本之间的关系 1.1、Oracle JDK与OpenJDK的区别 1.Oracle JDK是基于OpenJDK源代码构建的,因此Oracle JDK和OpenJDK之间没有重大的技术差异。 2.Oracle JDK将更多地关注稳定性,它重视更多的企业级用户,而OpenJDK经常发布以支持其他性能…...

2023年下半年软考考试重磅消息
重磅消息一:科目连考,分批考试 2023年下半年软考考试,采取科目连考、分批次考试的方式。 什么是科目连考? 连考就是第一个科目作答结束交卷完成后,自动进入第二个科目的考试,第一个科目剩余的时长可为第二…...
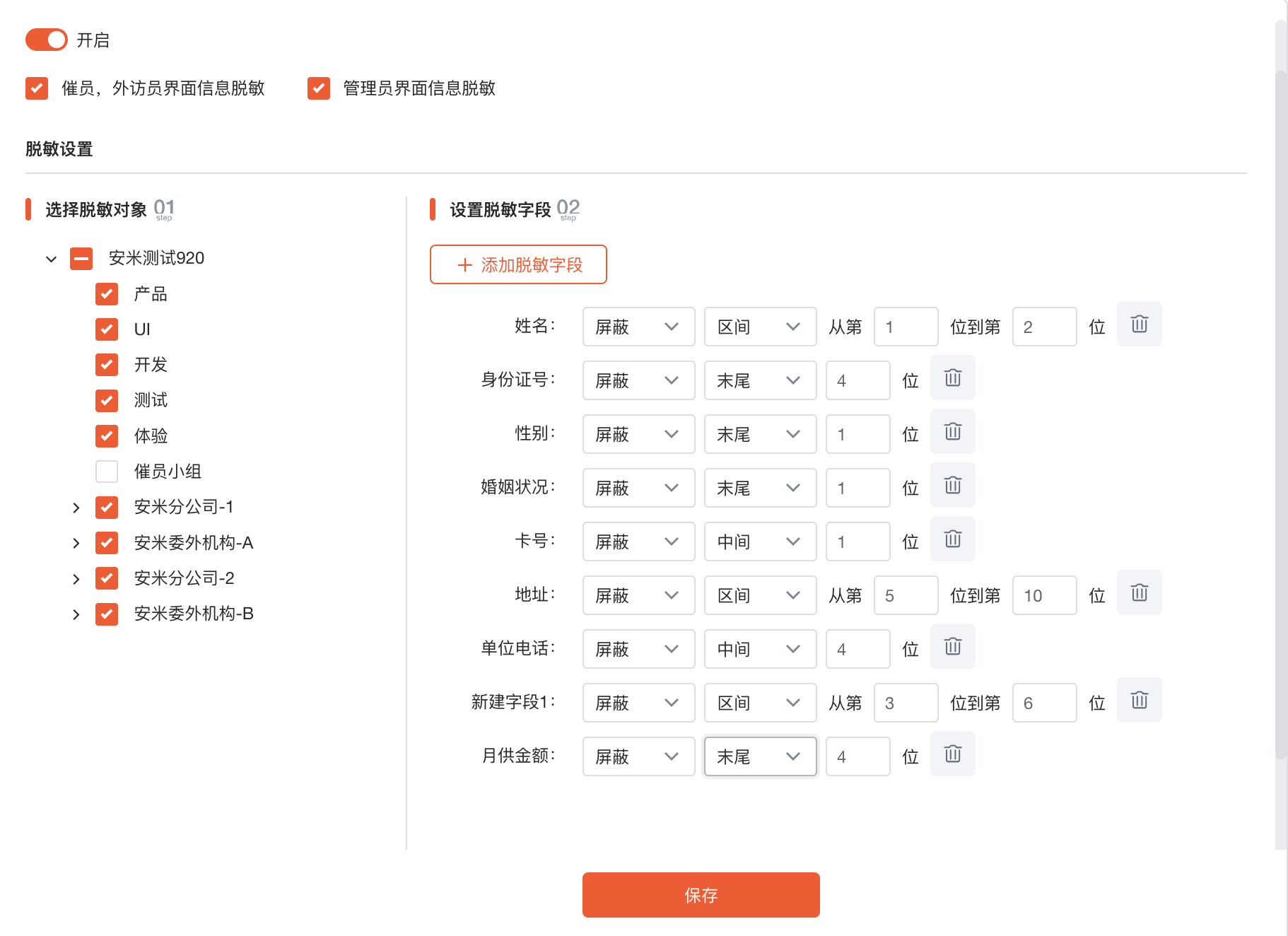
Spring Boot如何优雅实现动态灵活可配置的高性能数据脱敏功能
1.背景 在当下互联网高速发展的时代下,涉及到用户的隐私数据安全越发重要,一旦泄露将造成不可估量的后果。所以现在的业务系统开发中都会对用户隐私数据加密之后存储落库,同时还要求后端返回数据给前台之前进行数据脱敏。所谓脱敏处理其实就…...

九月 Web3 游戏报告:数量增长,巨头入场,用户获取和留存仍存挑战
作者: stellafootprint.network 9 月份,比特币价格窄幅波动,小幅上涨 3.7%。Web3 游戏行业正在增长,但月活跃用户超过 1,000 人的游戏仍不足 10%。不同公链上的游戏分布相对稳定,其中 BNB 以 30.9% 的份额领先。 随着 Web3 游戏…...

Scala语言入门
学习了这么久让我们来回顾一下之前的内容吧 Hadoop生态体系知识串讲 Scala编程语言 一、概述 http://scala-lang.org 专门为计算而生的语言,Scala将(Java后者C)面向对象设计和函数式编程结合在一起的简洁的高级编程语言。而函数式编程强调的是通过传递算子&…...

MyBatisPlus-02
一 查询条件的三种 1.按条件查询 //方式一:按条件查询QueryWrapper qw new QueryWrapper();qw.lt("age",18);List<User> userList userDao.selectList(qw);System.out.println(userList); 2.lambda格式按条件查询 //方式二:lambda格…...
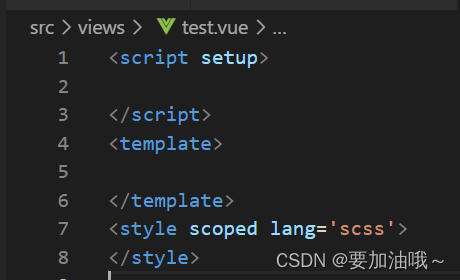
vscode中快速生成vue3模板
步骤:设置 -> 用户代码片段 -> vue.json(没有vue.json,选vue也可)-> 定义自己所需的代码段 代码段 如下, {"Print to console": {"prefix": "vue3", //键入该值,按tab…...

Liunx C运算符
一、运算符 (一)算数运算符 1、float和double不能进行取余操作。 (二)关系运算符 1、逻辑非 2、逻辑与 例子: if((a-1)<b&&b) 如果为真则自增,为假不自增 3、逻辑或 …...

【反射】Class类
Class类中包含了类定义的详细信息,可以使用Class类中提供的方法来获取,下面我们先获取Class对象,再介绍Class类中提供的获取类信息的方法。 一、准备工作 在src/test/java目录的cn.horse.reflect.entity包下新建BaseEntity类、UserInfoEnti…...
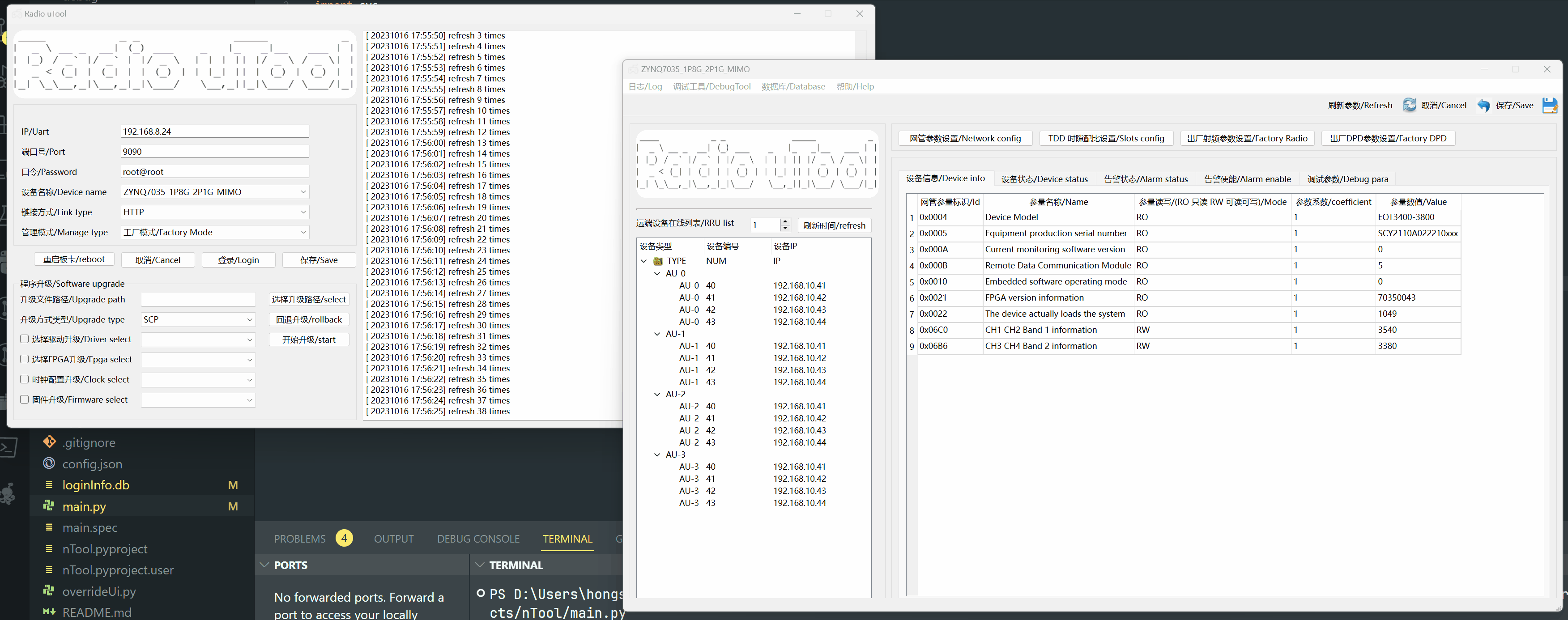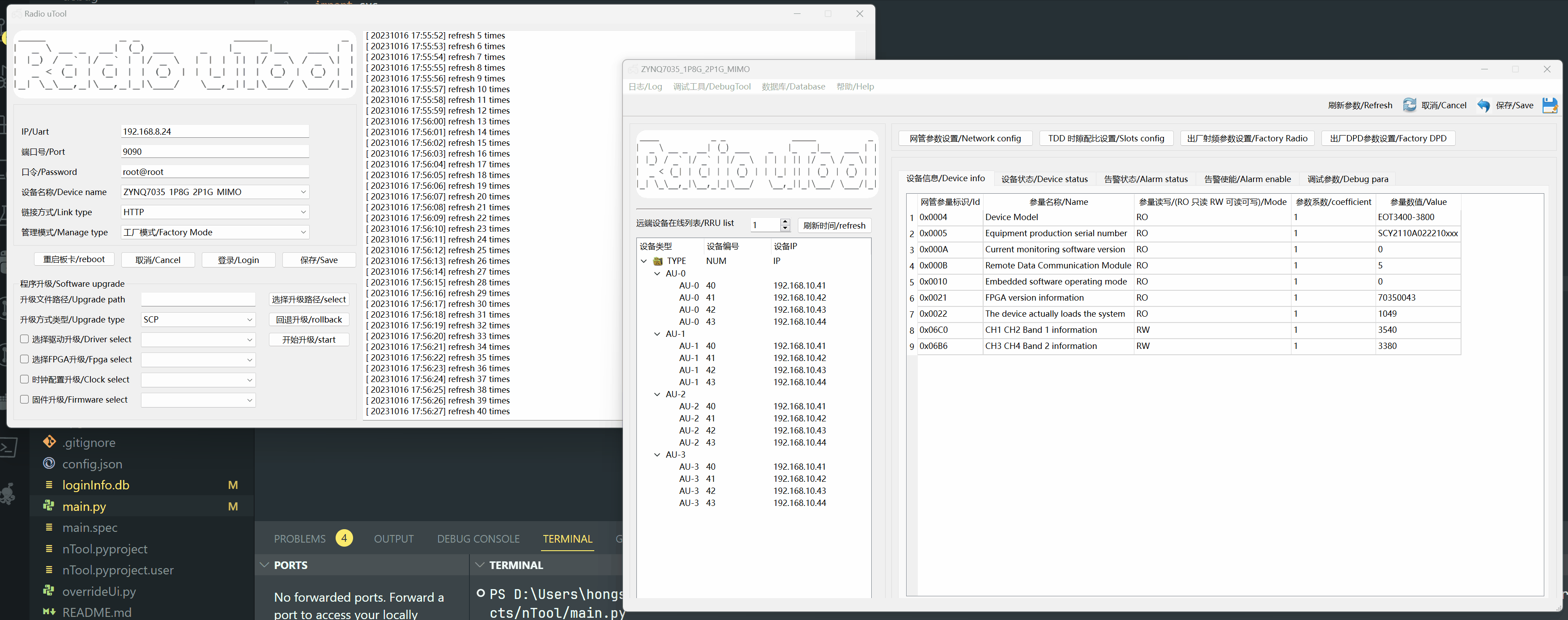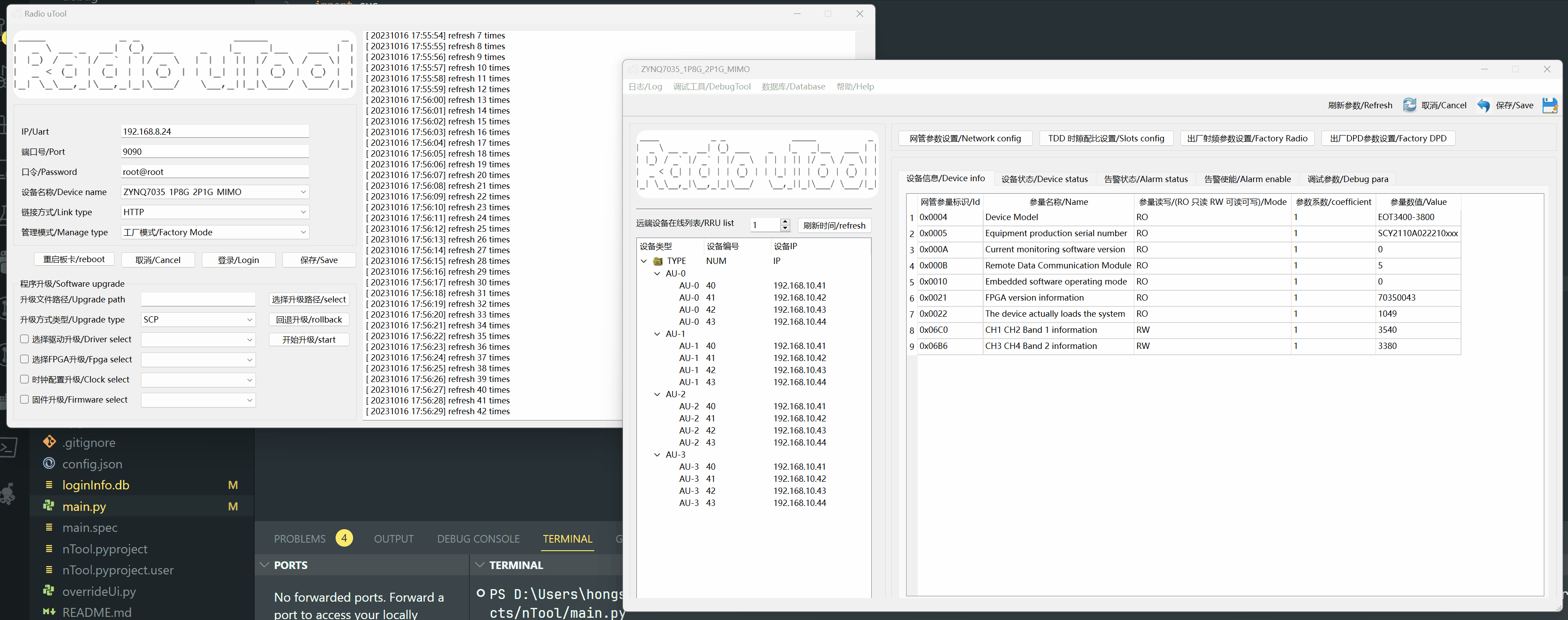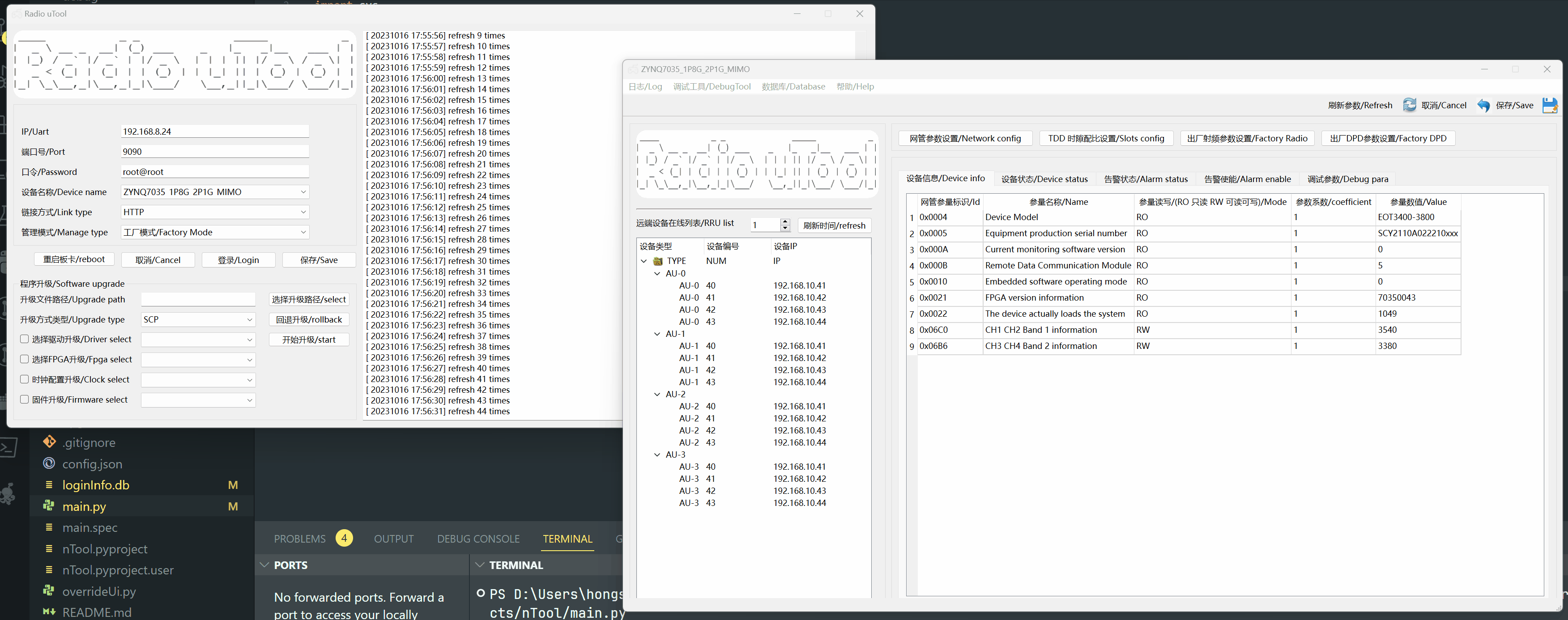
PyQt 问题记录
1.现成的组件不一定线程安全,(包括且不限于数据的修改竞争,和一些组件的崩溃 ) 对于PyQt 的线程使用,可能还需要更谨慎些 保存逻辑 QuestionBox("保存/Save")def Save(self):okFlagFalseerrFlagFalseWriteCmd{}for it in self.Mode…...

云安全—责任共担
0x00 前言 云安全的职责范围实际上一直遵循的是,谁提供谁负责,如果交付给云消费者的时候,交付者使用过程中就要自行负责,也就是我们经常遇到的配置不当等问题,在三层服务模式中,责任互相嵌套,最…...

使用Vscode终端设置window环境变量设置不上
问题描述 在Vscode中打开了一个终端,然后输入 set ENVprod, 但是我使用node 的proces.env.ENV并没有获取到 问题原因 可能是Vscode终端的问题,可以通过电脑自带的CMD去设置环境变量,通过echo查看,发现是没有问题的。...

【微信小程序】自定义组件布局会议OA其他页面(附源码)
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《微信小程序开发实战》。🎯Ἲ…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
