当前位置： 首页 > news >正文

YoloV8改进策略：SwiftFormer，全网首发，独家改进的高效加性注意力用于实时移动视觉应用的模型，重构YoloV8

news 2026/2/11 0:24:53

文章目录

  • 摘要
  • 论文：《SwiftFormer：基于Transformer的高效加性注意力用于实时移动视觉应用的模型》
  • 1、简介
  • 2、相关研究
  • 3、方法
    • 3.1、注意力模块概述
    • 3.2、高效的加性注意力
    • 3.3、SwiftFormer 架构
  • 4、实验
    • 4.1、实现细节
    • 4.2、基线比较
    • 4.3、图像分类
    • 4.4、目标检测和实例分割
    • 4.5、语义分割
  • 5、结论
  • 6、补充材料
    • A、SwiftFormer的架构细节
    • B、其他实现细节
    • C、额外消融
    • D、COCO数据集的误差分析
    • E、定性结果<

相关文章：

YoloV8改进策略：SwiftFormer，全网首发，独家改进的高效加性注意力用于实时移动视觉应用的模型，重构YoloV8

文章目录 摘要论文：《SwiftFormer：基于Transformer的高效加性注意力用于实时移动视觉应用的模型》1、简介2、相关研究3、方法3.1、注意力模块概述3.2、高效的加性注意力3.3、SwiftFormer 架构4、实验4.1、实现细节4.2、基线比较4.3、图像分类4.4、目标检测和实例分割4.5、语义…...

编程日记 2023/10/19 18:17:32

Jupyter Notebook在指定位置打开

1、在Jupyter Notebook设置文件中修改默认路径 anconda prompt输入&#xff1a; jupyter notebook --generate-config 找到配置文件路径&#xff1a;C:\Users\Lenovo.jupyter 打开文件&#xff0c;修改默认路径&#xff1a; ## The directory to use for notebooks and kernel…...

编程日记 2023/10/19 18:16:31

树控件的使用

目录 1、修改树控件的基础属性&#xff1a; 2、准备图标 &#xff1a; &#xff08;1&#xff09;、ico后缀的图片放入当前文件路径的rc中 &#xff08;2&#xff09;、在Icon中添加资源&#xff0c;导入图片 &#xff08;3&#xff09;、准备HICON图标 &#xff08;4&am…...

编程日记 2023/10/19 18:15:30

C++实现顺序栈类的定义，编写main ()函数验证顺序栈类设计的合理性

C实现顺序栈类的定义&#xff0c;编写main ()函数验证顺序栈类设计的合理性 以下是一个简单的C代码示例&#xff0c;用于实现顺序栈类的定义并编写main()函数来验证其合理性&#xff1a; #include <iostream> using namespace std;const int MAX_SIZE 100; // 定义栈的…...

编程日记 2023/10/19 18:14:28

手机直播助手软件app哪个好用？

手机直播助手软件现在可谓是多如牛毛&#xff0c;从上半年魔棒手机自动直播软件上线以来。几乎全国所有的科技公司都效仿魔棒手机自动直播软件兴起手机直播助手开发热。相对来说&#xff0c;简单的手机直播助手软件没什么技术门槛。但是手机无人直播助手软件要做精做全则很难。…...

编程日记 2023/10/19 18:13:27

腾讯待办宣布关停，哪款待办事项提醒APP好？

如果你之前一直使用微信中的“腾讯待办”小程序来记录待办事项并设置定时提醒&#xff0c;那么你就会发现腾讯待办在2023年10月16日通过其官方微信公众号、小程序发布了业务关停公告&#xff0c;将于2023年12月20日全面停止运营并下架&#xff0c;并且有导出数据的提示。 腾讯…...

编程日记 2023/10/19 18:12:26

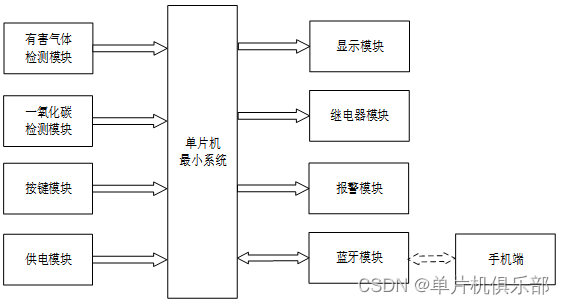
【单片机毕业设计】【hj-006-7】CO、有害混合气体检测 | 空气质量检测 | 有害气体检测

一、基本介绍 项目名&#xff1a; 基于单片机的CO、有害混合气体检测系统设计 基于单片机的空气质量检测系统设计 基于单片机的有害气体检测系统设计 项目编号&#xff1a;mcuclub-hj-006-7 单片机类型&#xff1a;STC89C52 具体功能&#xff1a; 1、通过MQ-7检测CO值&#x…...

编程日记 2023/10/19 18:11:25

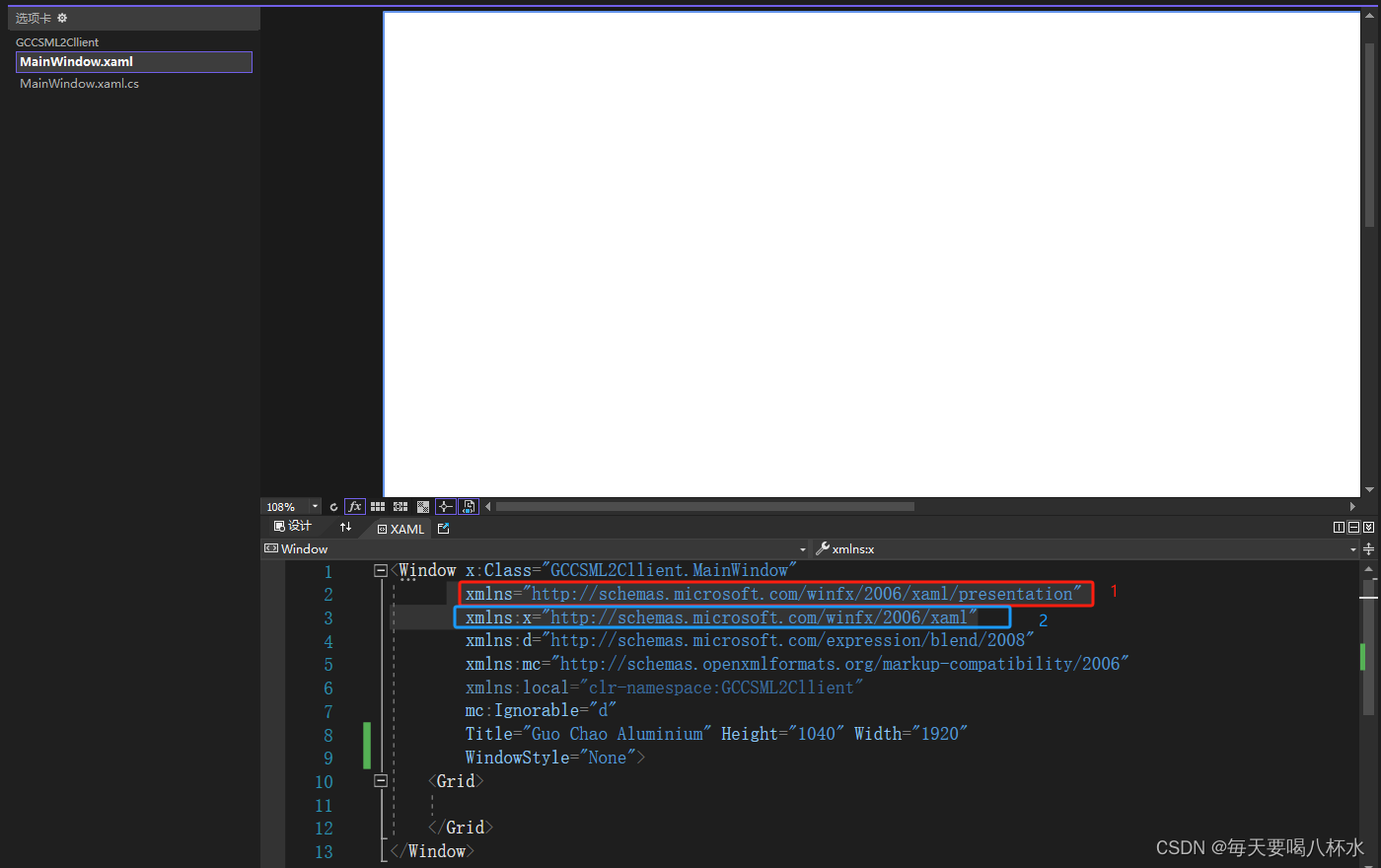
wpf主页面解析

1、 开头的网址作用 1和2都是引入命名空间的&#xff0c;每一个字符串代表一系列的命名空间&#xff0c;这样就可以不用一个一个引用了。wpf中规定有一个名称空间是可以不加名字的&#xff0c;xmlns不加名字是默认命名空间。 "http://schemas.microsoft.com/winfx/2006/x…...

编程日记 2023/10/19 18:10:24

三相交错LLC软启动控制程序算法实现---充电桩电源设计实战细节

简介 充电桩充电终端是一款单枪最大功率达到600kW的充电桩。它具有以下特点： 充电枪线长3.5米，重量小于90kg，额定电压1000V，最大电流600A，最大功率600kW。 高宽深为1700340295mm。 该充电桩采用模块化设计，具有较高的可靠性和可维护性。 充电时间大约在30分钟左右，…...

编程日记 2023/10/19 18:09:24

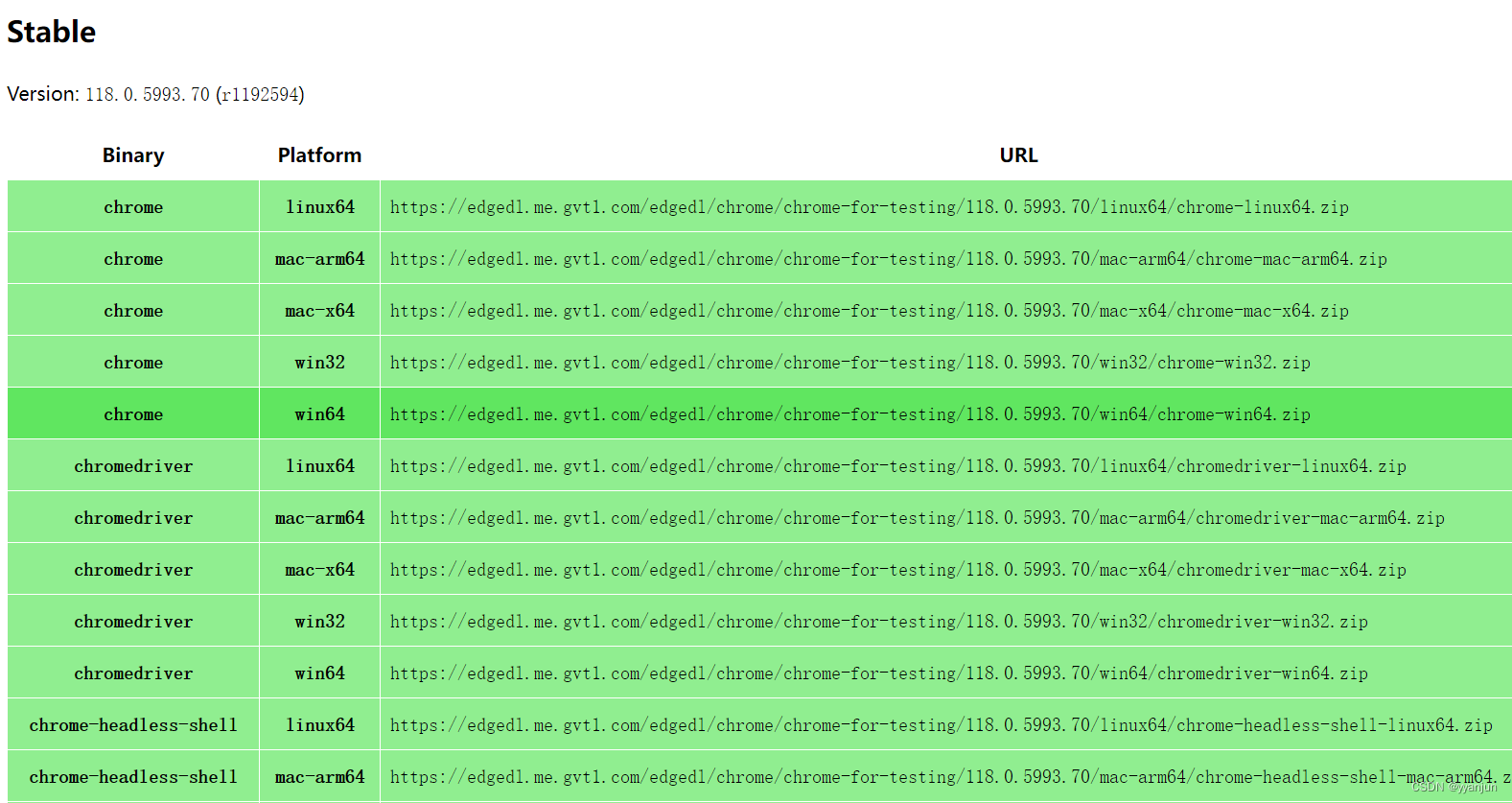
Chrome 115之后的版本，安装和使用chromedriver

在Python中使用selenium 时报如下错误&#xff1a; 1. 老版本chrome对应的chromedriver 下载地址&#xff1a;CNPM Binaries Mirror 2. 新版本chrome对应的chromedriver 下载地址&#xff1a;Chrome for Testing availability...

编程日记 2023/10/19 18:08:23

潮玩宇宙：收藏、交流与竞技的数字乐园

最近爆火的新项目潮玩宇宙&#xff0c;想必有很多人入场了&#xff0c;代理商宣传投资147一个月回本&#xff0c;确实是现在做到了&#xff0c;现在平台一颗宝石的价格已经超过美金了&#xff0c;还有一大部分人在等待进场&#xff0c;潮玩宇宙旗下奖券世界和养猪农场已经做了有…...

编程日记 2023/10/19 18:07:22

企拓客app骗局为不实信息，企拓客保持正常经营状态

网络运营软件盛行,带来了一些混乱的现状,造成企业不同程度的损失,也让运营单位在选择软件时心有余悸。真真假假的信息,扰乱了运营软件的市场环境,热门的拓客软件不慎躺枪。企拓客就是其中之一。 笔者通过网上检索的方式,最终查证企拓客软件官方保持着正常运营,企拓客app骗局不攻…...

编程日记 2023/10/19 18:06:21

【性能】JDK和Jmeter的安装与配置

一、JDK环境配置 1. 下载JDK 官网下载地址&#xff1a;http://www.oracle.com/technetwork/java/javase/downloads/java-archive-downloads-javase7-521261.html 选择对应系统的安装包&#xff0c;下载后安装&#xff0c;安装中记录JDK安装的地址&#xff0c;之后一直点击下一…...

编程日记 2023/10/19 18:05:20

02_单片机及开发板介绍

单片机简介 单片机&#xff0c;又称为微控制器&#xff08;Microcontroller&#xff09;&#xff0c;是一种集成了微处理器核心、存储器、输入/输出接口及各种功能模块的集成电路芯片。它通常由中央处理器&#xff08;CPU&#xff09;、存储器、输入/输出接口以及各种外设组成&…...

编程日记 2023/10/19 18:04:19

华测监测预警系统 2.2---任意文件读取漏洞

目录 1. 资产搜集 2. 漏洞复现 3. 实战总结 1. 资产搜集 直接上fofa 和 hunter 个人推荐hunter可以看到icp备案公司直接提交盒子就行了 FOFA语法 app”华测监测预警系统2.2” Hunter语法 web.body”华测监测预警系统2.2” 2. 漏洞复现 这里手动复现的&#xff0c;目录是/…...

编程日记 2023/10/19 18:03:18

新版多功能去水印工具微信小程序源码下载+带流量主功能

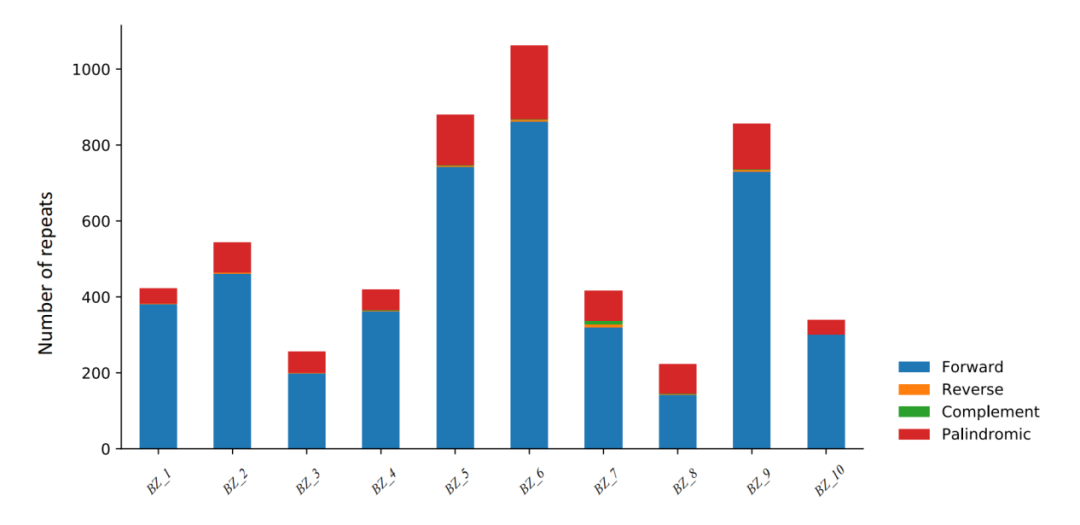
新版多功能去水印工具微信小程序源码下载&#xff0c;带流量主功能。自带去水印接口的多功能小程序&#xff0c;支持各大平台短视频去水印。 支持保存封面、图集、标题等等&#xff1b;支持本地图片去水印&#xff1b;支持图片拼接&#xff1b;支持九宫格切图&#xff1b;支持修…...

编程日记 2023/10/19 18:01:14

文章必备| 叶绿体基因组高级分析内容汇总

叶绿体普遍存在于植物体中&#xff0c;叶绿体基因组是一个典型的双链环状DNA分子&#xff0c;一个植物当中含有多个叶绿体&#xff0c;一个叶绿体中含有12个cpDNA分子。 常见的植物叶绿体基因组大小一般在150-160 kb左右&#xff0c;藻类会略小一些&#xff0c;在80-100 kb左右…...

编程日记 2023/10/19 18:00:13

阿里实习JAVA后端面经总结

暑期实习面试阿里Java后端岗位的一面的面经。 主要拷打了项目+Java 集合+Java并发+网络+mysql，一场面试大概问了 20 个题目，问的还是比较基础，不算太难。 问题记录 简历上有两个项目，选一个你比较熟悉的介绍 （略） 项目用到了哪个线程实现类？ 用了ScheduledThreadP…...

编程日记 2023/10/19 17:59:13

利用 NLP 超能力：一步步介绍Hugging Face微调教程

导入必要的库 导入必要的库类似于为特定编程和数据分析活动构建工具包。这些库通常是预先编写的代码集合，提供广泛的功能和工具，有助于加快开发速度。开发人员和数据科学家可以通过导入适当的库来访问新功能、提高生产力并使用现有解决方案。 import pandas as pd import n…...

编程日记 2023/10/19 17:58:11

凝聚技术力量 共建测试生态 ——集成电路测试技术交流日成功举办

10月18日下午&#xff0c;凝聚技术力量&#xff0c;共建测试生态 ——集成电路测试技术交流会在上海成功举办。来自全国各地知名专家学者、技术大咖及企业代表齐聚一堂&#xff0c;共同探讨封装测试技术的发展方向&#xff0c;共话产业未来&#xff0c;共促产业发展。 本次活动…...

编程日记 2023/10/19 17:57:10

wordpress后台更新后 前端没变化的解决方法

使用siteground主机的wordpress网站&#xff0c;会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后&#xff0c;网站没有变化的情况。 不熟悉siteground主机的新手&#xff0c;遇到这个问题&#xff0c;就很抓狂&#xff0c;明明是哪都没操作错误&#x…...

编程新知 2026/2/10 23:40:48

【JVM】- 内存结构

引言 JVM&#xff1a;Java Virtual Machine 定义&#xff1a;Java虚拟机&#xff0c;Java二进制字节码的运行环境好处&#xff1a; 一次编写&#xff0c;到处运行自动内存管理&#xff0c;垃圾回收的功能数组下标越界检查&#xff08;会抛异常&#xff0c;不会覆盖到其他代码…...

编程新知 2026/1/30 13:40:43

STM32标准库-DMA直接存储器存取

文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA&#xff08;Direct Memory Access&#xff09;直接存储器存取 DMA可以提供外设…...

编程新知 2026/1/26 10:55:51

高等数学（下）题型笔记（八）空间解析几何与向量代数

目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

编程新知 2026/1/28 9:04:29

Spring AI与Spring Modulith核心技术解析

Spring AI核心架构解析 Spring AI&#xff08;https://spring.io/projects/spring-ai&#xff09;作为Spring生态中的AI集成框架&#xff0c;其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似&#xff0c;但特别为多语…...

编程新知 2025/12/14 17:38:21

深入理解Optional：处理空指针异常

1. 使用Optional处理可能为空的集合 在Java开发中&#xff0c;集合判空是一个常见但容易出错的场景。传统方式虽然可行&#xff0c;但存在一些潜在问题&#xff1a; // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

编程新知 2025/12/19 19:15:39

【前端异常】JavaScript错误处理：分析 Uncaught (in promise) error

在前端开发中&#xff0c;JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作&#xff08;如 Promise、async/await 等&#xff09;&#xff0c;开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝&#xff08;r…...

编程新知 2026/1/1 23:11:45

uni-app学习笔记三十五--扩展组件的安装和使用

由于内置组件不能满足日常开发需要&#xff0c;uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件&#xff0c;需要安装才能使用。 一、安装扩展插件 安装方法&#xff1a; 1.访问uniapp官方文档组件部分&#xff1a;组件使用的入门教程 | uni-app官网 点击左侧…...

编程新知 2026/2/6 5:51:39

基于江科大stm32屏幕驱动，实现OLED多级菜单（动画效果），结构体链表实现(独创源码)

引言 在嵌入式系统中&#xff0c;用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例&#xff0c;介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单&#xff0c;执行相应操作&#xff0c;并提供平滑的滚动动画效果。 本文设计了一个…...

编程新知 2026/2/6 5:58:36

链式法则中 复合函数的推导路径 多变量“信息传递路径”

非常好&#xff0c;我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题&#xff0c;统一使用 二重复合函数&#xff1a; z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y))​ 来全面说明。我们会展示其全微分形式&#xff08;偏导…...

编程新知 2026/2/8 12:07:50