【进击的算法】动态规划——不同维度的背包问题
文章目录
- 前言
- 动态规划的维度
- 二维动规
- leetcode416、分割等和子集
- leetcode1049. 最后一块石头的重量 II
- leetcode494、目标和
- 三维动规
- leetcode474. 一和零
- 结语
前言
大家好久不见,这次我们一起来学习一下动态规划中怎么确定维度,和对应问题如何解决。
动态规划的维度
一个维度:只有物品
两个维度:物品和容量
三个维度:物品和容量1和容量2
之前讲解动态规划问题时,斐波那契数列就是一个很简单的一维动态规划问题,因为我们要考虑的状态只有这个数的值,(一维动态规划),之后讲解了01背包问题,也就是有了第二个维度,不仅要考虑物品,还要考虑背包容量(二维动态规划)
其实在这里一定要明确好状态到底是什么,在我看来:与要求结果相关的状态,都是可以列为维度的,我们是将物品范围和背包容量都列为了状态因为他们都会影响结果
二维动规
leetcode416、分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
- 示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。- 示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
这个问题要我们寻找等和的子集,我们可以把nums数组里的元素抽象为背包问题里的石头,把分成的两个等和子集抽象为背包。
-
dp[i][j] 表示
前i个元素放到容量为j的背包的最大重量! -
dp[i][j] = max(dp[i-1][j],dp[i-1][j-nums[i]]+nums[i])
就算压缩为一维动态规划,那也是压缩的空间而已,本质上我们还是定义了两个状态!
#define MAX(a,b) ((a)>(b)?(a):(b))bool canPartition(int* nums, int numsSize){int sum = 0;for(int i = 0;i<numsSize;i++){sum+=nums[i];}if(sum%2 != 0) return false;int target = sum / 2;int* dp = (int*)calloc(sizeof(int),target+1);//先遍历物品,再遍历列!for(int i = 0;i<numsSize;i++){for(int j = target;j>=nums[i];j--){dp[j] = MAX(dp[j],dp[j-nums[i]]+nums[i]);}} if(dp[target] == target) return true;return false;
}
leetcode1049. 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
这道题目,我们要获得撞后剩下的最小质量,只需要将这堆石头尽可能分为两堆一样重量的石头,相互碰撞即可。
在这道题目里,nums数组里的元素是石块,总重量的一半即是背包容量,我们要尽可能填满这一半的石头。
- dp[i][j] ——前i个石块放入j的背包的最大重量。
- dp[i][j] = max(dp[i-1][j],dp[i-1][j-nums[i]]+nums[i])
优化思路也和01背包问题一样,即滚动数组压缩
参考代码:
#define MAX(a,b) ((a)>(b)?(a):(b))
int lastStoneWeightII(int* stones, int stonesSize){int sum = 0;for(int i = 0;i<stonesSize;i++){sum += stones[i];}int target = sum/2;int dp[1501] = {0};for(int i = 0;i<stonesSize;i++)//遍历物品{for(int j = target;j>=stones[i];j--){dp[j] = MAX(dp[j],dp[j-stones[i]]+stones[i]);}}return sum - dp[target] - dp[target];
}
leetcode494、目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
这道问题其实也是要我们分为两组,本质上nums数组里的元素就是石块,分组的大小仍然是背包大小。唯一不同的是我们dp数组在定义上变成了要求多少种方法
- dp[i][j] ——前i个元素放入容量为j的背包,有多少种方法?
- dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]]; //可以放也可以不放两者加起来就是总方法数
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {//分组背包问题,一组放+,一组放-,凑成targetint sum = 0;for(auto e : nums){sum+=e;}//left rightif(abs(target) > sum) return 0;if((target + sum)%2 == 1) return 0;int left = (target + sum)/2;vector<int> dp(left+1,0);dp[0] = 1;for(int i = 0;i<nums.size();i++){for(int j = left;j>=nums[i];j--){dp[j] += dp[j-nums[i]];}}return dp[left];}
};
三维动规
leetcode474. 一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ,因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
说白话就是用j个0和k个1最多能凑成几个nums中的字符串
这道题可以将数组里的元素抽象为石头,0和1的数量抽象为背包容量,很显然现在有两个背包容量
- dp[i][j][k]——在前 i 个字符串中,使用 j 个 0 和 k 个 1的情况下最多可以得到的字符串数量。
- dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-num1][k-num0] + 1);
其实就是要不要把这个字符串放进来,比一下大的就行
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0//dp[i][j] 表示容量为ij的背包能装的最大重量!for(string str : strs){int onenum = 0,zeronum = 0;for(char c : str){if(c == '1')onenum++;elsezeronum++;}for(int i = m;i>=zeronum;i--){for(int j = n;j>=onenum;j--){dp[i][j] = max(dp[i][j],dp[i-zeronum][j-onenum]+1);}}}return dp[m][n];}
};
结语
到这里本篇文章就结束了,希望能对你学习动态规划有所帮助,我们下次见~
相关文章:

【进击的算法】动态规划——不同维度的背包问题
文章目录前言动态规划的维度二维动规leetcode416、分割等和子集leetcode1049. 最后一块石头的重量 IIleetcode494、目标和三维动规leetcode474. 一和零结语前言 大家好久不见,这次我们一起来学习一下动态规划中怎么确定维度,和对应问题如何解决。 动态…...
udiMagic 导入 Excel to Tally ERP Crack
关于 udiMagic 软件 udiMagic 是一款可帮助您快速轻松地将数据导入 Tally ERP 的应用程序。它由 Shweta Softwares 创建和分发,于2007 年首次推出。 您可以在 USB 闪存驱动器 [旅行许可证] 中携带 udiMagic,并在具有任何 Tally 版本的任何计算机上使用…...

Redis实现分页和多条件模糊查询方案
导言 Redis是一个高效的内存数据库,它支持包括String、List、Set、SortedSet和Hash等数据类型的存储,在Redis中通常根据数据的key查询其value值,Redis没有模糊条件查询,在面对一些需要分页、排序以及条件查询的场景时(如评论&…...

【H5 | CSS | JS】如何实现网页打字机效果?快收下这份超详细指南(附源码)
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学会计学专业大二本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后…...

Airbyte,数据集成的未来
Gartner 曾预计,到 2025 年,80% 寻求扩展数字业务的组织将失败。因为他们没有采用现代方法来进行数据和分析治理。数据生态是基础架构生态的最重要一环,数据的处理分发与计算,从始至终贯穿了整个数据流通生态。自从数据集中在数据…...

00.内容安排
内容安排如下01.Linux基本命令0.2 vim编辑器,gcc、gdb、makefile、动/静态库制作使用03.文件 I/O 常用函数、文件读写原理、进程控制快概念、阻塞、非阻塞概念04.文件常用操作函数、目录常用操作函数、重定向05.进程控制fork、exec函数组、进程回收 wait/waitpid06.…...
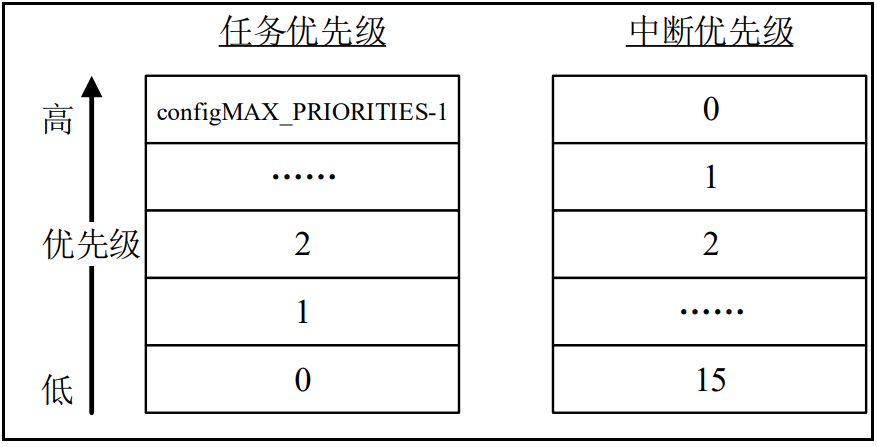
FreeRTOS任务基础知识
单任务和多任务系统单任务系统单任务系统的编程方式,即裸机的编程方式,这种编程方式的框架一般都是在main()函数中使用一个大循环,在循环中顺序的执行相应的函数以处理相应的事务,这个大循环的部分可以视为…...
JDBC-API详解、SQL注入演示、连接池
文章目录JDBC1,JDBC概述1.1 JDBC概念1.2 JDBC本质1.3 JDBC好处2,JDBC快速入门2.1 编写代码步骤2.2 具体操作3,JDBC API详解3.1 DriverManager3.2 Connection (事务归我管)3.2.1 获取执行对象3.2.2 事务管理3.3 Stateme…...
)
C 学习笔记 —— 动态分配内存(malloc)
文章目录分配内存malloccallocrealloc创建数组方式free的重要性举例常见动态分配内存错误忘记检查所请求的内存对NULL指针进行解引用对分配的内存越界访问释放一块内存后,继续使用释放一块内存的一部分是不允许的内存泄漏分配内存 当一个数组声明时,需要…...

RK3588通用布线设计指南
(1)走线长度应包含过孔和封装。(2)由于表贴器件的焊盘会导致阻抗降低,为减小阻抗突变的影响,建议在表贴焊盘的正下方按焊盘大小挖去一层参考层。常用的表贴器件有:电容、 ESD、共模抑制电感、连…...

ChatGPT也懂如何设计开发板!?
到底应该如何设计一款开发板?我们问了一下最近风很大的ChatGPT,得出了这样的回答: 或者这样的回答: 显而易见,RK3568开发板是一款功能丰富,性能优异,易于开发的高性能开发板,适用于各…...
去了字节跳动,才知道年薪40W的测试居然有这么多?
今年大环境不好,内卷的厉害,薪资待遇好的工作机会更是难得。最近脉脉职言区有一条讨论火了: 哪家互联网公司薪资最‘厉害’? 下面的评论多为字节跳动,还炸出了很多年薪40W的测试工程师 我只想问一句,现在的…...

2023前端面试知识点总结
原型 JavaScript中的对象都有一个特殊的 prototype 内置属性,其实就是对其他对象的引用 几乎所有的对象在创建时 prototype 属性都会被赋予一个非空的值,我们可以把这个属性当作一个备用的仓库 当试图引用对象的属性时会出发get操作,第一步时…...
FL StudioV21电脑版水果编曲音乐编辑软件
这是一款功能十分丰富和强大的音乐编辑软件,能够帮助用户进行编曲、剪辑、录音、混音等操作,让用户能够全面地调整音频。FL水果最新版是一款专业级别的音乐编曲软件,集合更多的编曲功能为一身,可以进行录音、编辑、制作、混音、调…...

【数据结构初阶】实现顺序表的简单功能
目录一.线性表和顺序表的概念二.顺序表的实现1.动态顺序表的创建2.初始化顺序表3.打印顺序表4.销毁顺序表5.检查容量6.头插 尾插7.头删 尾删三.使用下标插入删除1.删除指定位置2.向指定位置插入指定数一.线性表和顺序表的概念 线性表是n个具有相同特性的数据元素的有限序列。 线…...

华为OD机试题,用 Java 解【停车场车辆统计】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

Linux中使用Docker部署Mysql数据库
前言 和朋友一起搞一个项目,分了一下工作,但是mysql迟迟安装不上,程序都在一个环境里确实容易出现很多问题,浪费时间和经历在这些配置上,好在有docker了,就在docker里搭建一个Mysql数据库使用吧࿰…...
使用步骤)
JPDA(远程调试)使用步骤
JPDA(Java Plateform Debugger Architecture) 更改启动脚本 vi catalina.sh 127行 CATALINA_OPTS “-Xdebug -Xrunjdwp:transportdt_socket,servery,suspendn,address5888” 指定端口,默认是8000 377行以jpda方式启动tomcat ./catalina.sh jpda start tomcat以这个…...
磷脂-聚乙二醇-丙烯酸酯;DSPE-PEG-AC试剂说明;DSPE-PEG-Acrylate科研用
中文名称:磷脂-聚乙二醇-丙烯酸酯 丙烯酸酯-聚乙二醇-磷脂 简称:DSPE-PEG-AC;DSPE-PEG-Acrylate 溶剂:溶于部分常规有机溶剂 PEG分子量:1000;2000;3400;5000等等 注意事项:避免…...

C++入门:异常处理
异常是程序在执行期间产生的问题。C 异常是指在程序运行时发生的特殊情况,比如尝试除以零的操作。异常提供了一种转移程序控制权的方式。C 异常处理涉及到三个关键字:try、catch、throw。throw: 当问题出现时,程序会抛出一个异常。这是通过使…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
