当前位置： 首页 > news >正文

Hive安装配置 - 内嵌模式

news 2026/2/11 1:21:05

文章目录

  • 一、Hive运行模式
  • 二、安装配置内嵌模式Hive
    • （一）下载hive安装包
    • （二）上传hive安装包
    • （三）解压缩hive安装包
    • （四）配置hive环境变量
    • （五）关联Hadoop
    • （六）创建数据仓库目录
    • （七）设置Derby数据库的位置
    • （八）初始化元数据信息
    • （九）启动Hive CLI
    • （十）验证多用户访问

一、Hive运行模式

  • Hive有三种运行模式：内嵌模式、本地模式和远程模式
    在这里插入图片描述

二、安装配置内嵌模式Hive

在这里插入图片描述

（一）下载hive安装包

（二）上传hive安装包

（三）解压缩hive安装包

（四）配置hive环境变量

（五）关联Hadoop

（六）创建数据仓库目录

（七）设置Derby数据库的位置

（八）初始化元数据信息

（九）启动Hive CLI

（十）验证多用户访问

相关文章：

Hive安装配置 - 内嵌模式

文章目录 一、Hive运行模式二、安装配置内嵌模式Hive（一）下载hive安装包（二）上传hive安装包（三）解压缩hive安装包（四）配置hive环境变量（五）关联Hadoop&#x…...

编程日记 2023/10/19 19:22:46

html中登录按钮添加回车键登录

原文链接有3种方法&#xff0c;其它2中不会弄&#xff0c;第二种方法成功&#xff0c;下面详细说说 原html的登录部分是 <button class"btn btn-success btn-block waves-effect waves-light" id"button" >登入</button> 在该html中增加 &…...

编程日记 2023/10/19 19:21:45

PCL 空间两平面交线计算

PCL 空间两平面交线计算 std::vector<float> LineInPlanes(std::vector<double> para1, std::vector<double> para2) {std::vector<float...

编程日记 2023/10/19 19:20:44

交替合并字符串

题目要求 给你两个字符串 word1 和 word2 。请你从 word1 开始&#xff0c;通过交替添加字母来合并字符串。如果一个字符串比另一个字符串长&#xff0c;就将多出来的字母追加到合并后字符串的末尾。 返回 合并后的字符串 。 示例 示例 1&#xff1a; 输入&#xff1a;word1 …...

编程日记 2023/10/19 19:19:43

Linux考试复习整理

文章目录 Linux考试整理一.选择题1.用户的密码现象放置在哪个文件夹&#xff1f;2.删除文件或目录的命令是&#xff1f;3.显示一个文件最后几行的命令是&#xff1f;4.删除一个用户并同时删除用户的主目录5.Linux配置文件一般放在什么目录&#xff1f;6.某文件的组外成员的权限…...

编程日记 2023/10/19 19:18:42

基于geojson-vt和canvas的高性能出图

概述 本文介绍基于geojson-vt和canvas&#xff0c;实现node端高性能出图。 效果 实现 1. canvas绘图 import { createCanvas } from canvasconst tileSize 256; const canvas createCanvas(tileSize, tileSize) const ctx canvas.getContext(2d)2. 处理geojson const g…...

编程日记 2023/10/19 19:17:41

CTF是黑客大赛？新手如何入门CTF？

CTF是啥 CTF 是 Capture The Flag 的简称&#xff0c;中文咱们叫夺旗赛&#xff0c;其本意是西方的一种传统运动。在比赛上两军会互相争夺旗帜&#xff0c;当有一方的旗帜已被敌军夺取&#xff0c;就代表了那一方的战败。在信息安全领域的 CTF 是说&#xff0c;通过各种攻击手…...

编程日记 2023/10/19 19:16:40

电脑开不了机用U盘重装系统Win10教程

如果我们遇到了电脑开不起机的问题&#xff0c;这给我们的正常使用带来了很大的影响。这时候我们可以借助U盘重装系统的方法&#xff0c;轻松应对这一问题。下面小编给大家详细介绍关于用U盘给开不机的电脑重装Win10系统的教程步骤&#xff0c;操作后用户就能正常使用电脑了。 …...

编程日记 2023/10/19 19:15:39

四叉堆在GO中的应用-定时任务timer

堆作为必须掌握的数据结构之一&#xff0c;在众多场景中也得到了广泛的应用。 比较典型的&#xff0c;如java中的优先队列PriorityQueue、算法中的TOP-K问题、最短路径Dijkstra算法等&#xff0c;在这些经典应用中堆都担任着灵魂般的角色。 理论基础 binary heap 再一起回忆…...

编程日记 2023/10/19 19:13:37

Flow深入浅出系列之使用Kotlin Flow自动刷新Android数据的策略

Flow深入浅出系列之在ViewModels中使用Kotlin FlowsFlow深入浅出系列之更聪明的分享 Kotlin FlowsFlow深入浅出系列之使用Kotlin Flow自动刷新Android数据的策略 Flow深入浅出系列之使用Kotlin Flow自动刷新Android数据的策略 讨论在Android应用程序中使用Kotlin Flow高效加载…...

编程日记 2023/10/19 19:12:36

AC修炼计划（AtCoder Regular Contest 165）

传送门&#xff1a;AtCoder Regular Contest 165 - AtCoder 本次习题参考了樱雪猫大佬的题解&#xff0c;大佬的题解传送门如下&#xff1a;Atcoder Regular Contest 165 - 樱雪喵 - 博客园 (cnblogs.com) A - Sum equals LCM 第一题不算特别难 B - Sliding Window Sort 2 对…...

编程日记 2023/10/19 19:11:35

【Express】登录鉴权 JWT

JWT&#xff08;JSON Web Token&#xff09;是一种用于实现身份验证和授权的开放标准。它是一种基于JSON的安全传输数据的方式&#xff0c;由三部分组成&#xff1a;头部、载荷和签名。 使用jsonwebtoken模块&#xff0c;你可以在Node.js应用程序中轻松生成和验证JWT。以下是j…...

编程日记 2023/10/19 19:09:32

【微服务 SpringCloud】实用篇 · Ribbon负载均衡

微服务&#xff08;4&#xff09; 文章目录 微服务&#xff08;4&#xff09;1. 负载均衡原理2. 源码跟踪1&#xff09;LoadBalancerIntercepor2&#xff09;LoadBalancerClient3&#xff09;负载均衡策略IRule4&#xff09;总结 3. 负载均衡策略3.1 负载均衡策略3.2 自定义负载…...

编程日记 2023/10/19 19:08:30

zabbix-proxy代理服务器配置

下载zabbix源 rpm -Uvh https://repo.zabbix.com/zabbix/5.0/rhel/7/x86_64/zabbix-release-5.0-1.el7.noarch.rpm 安装 yum -y install zabbix-proxy-mysql zabbix_get 查看相关文件路径 rpm -ql zabbix-proxy-mysql 创建数据库 mysq -uroot -proot mysql> create database…...

编程日记 2023/10/19 19:07:29

【python零基础入门学习】python进阶篇之OOP - 面向对象的程序设计

本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》&#xff1a;python零基础入门学习 《python运维脚本》&#xff1a; python运维脚本实践 《shell》&#xff1a;shell学习 《terraform》持续更新中&#xff1a;terraform_Aws学习零基础入门到最佳实战 《k8…...

编程日记 2023/10/19 19:06:28

中国xx集团信息技术工程师面试

进入面试间&#xff0c;坐着三位面试官&#xff0c;压力扑面而来&#xff0c;三位面试官先做了自我介绍&#xff0c;介绍了一下面试的流程后才开始面试。 一、自我介绍 不多说。 二、看你学过数据挖掘这门课&#xff0c;能简单介绍一下有哪些章节&#xff0c;学了些什么&…...

编程日记 2023/10/19 19:05:27

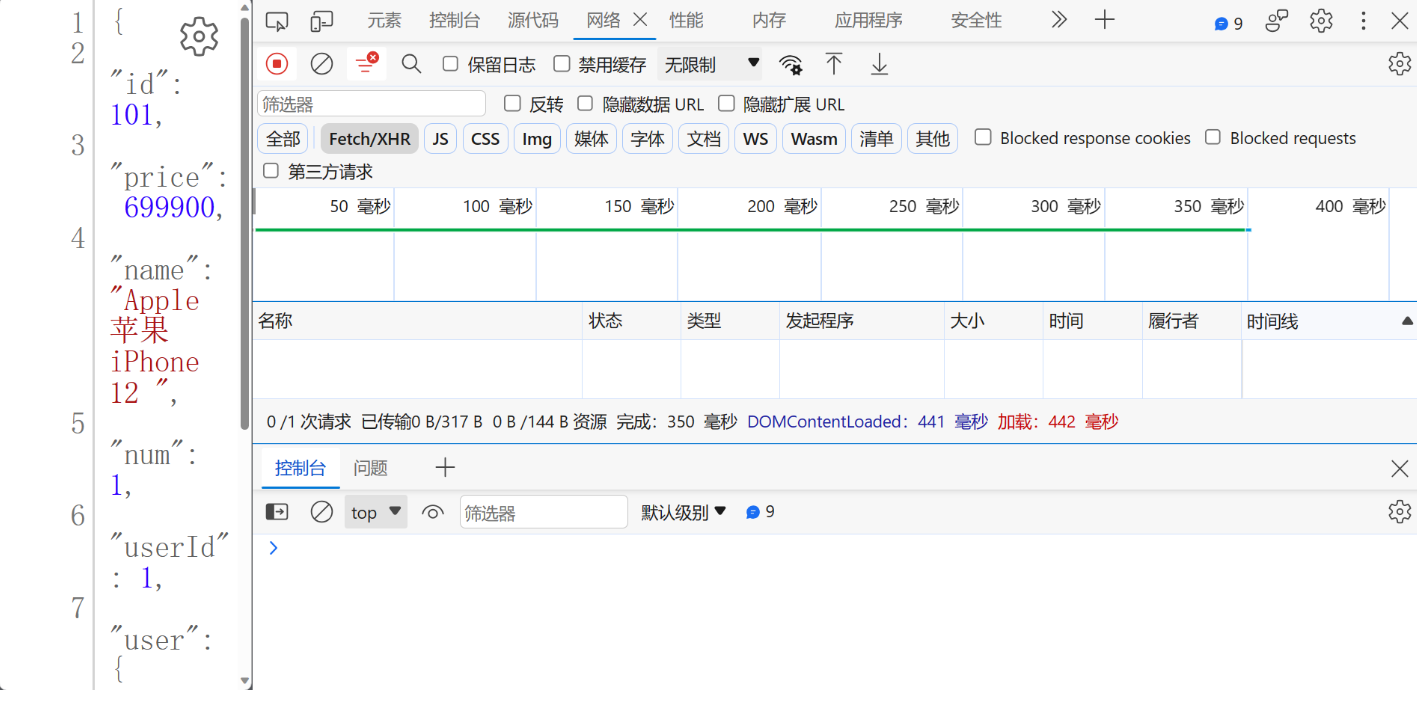
Jmeter接口自动化测试 —— Jmeter下载安装及入门

jmeter简介 Apache JMeter是Apache组织开发的基于Java的压力测试工具。用于对软件做压力测试&#xff0c;它最初被设计用于Web应用测试&#xff0c;但后来扩展到其他测试领域。 下载 下载地址&#xff1a;Apache JMeter - Download Apache JMeter 安装 由于Jmeter是基于Java的…...

编程日记 2023/10/19 19:04:26

ARM 学习笔记2 初识Cortex-M33与STM32G4

入门 ARM Cortex-M系列处理器的差异与联系&#xff1a;【ARM Cortex-M 系列 1 – Cortex-M0, M3, M4, M7, M33 差异】两本书籍的英文版和中文版 Definitive Guide to Arm Cortex-M23 and Cortex-M33 Processors Arm Cortex-M23和Cortex-M33微处理器权威指南ST的介绍页 Arm Cor…...

编程日记 2023/10/19 19:03:22

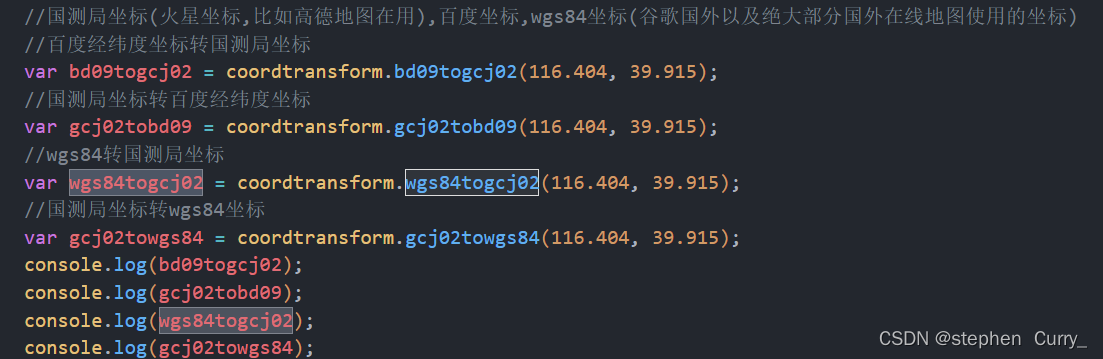
vue中使用coordtransform 互相转换坐标系

官方网站&#xff1a;https://www.npmjs.com/package/coordtransform 在使用高德sdk时&#xff0c;其返回的坐标在地图上显示时有几百米的偏移&#xff0c;这是由于高德用的是 火星坐标&#xff08;GCJ02&#xff09;&#xff0c;而不是wgs84坐标。为了消除偏移&#xff0c;将G…...

编程日记 2023/10/19 19:02:21

双线性插值详解

双线性插值的原理网上资料非常多，本文重点介绍双线性插值实现的两种方式: 角对齐(coner_align = True) 和 边对齐(coner_align = False)。两种不能的方式下去实现双线性插值，目标图像中的每个像素点，它是如何计算取值的，本文会通过原理结合代码的方式将实现细节讲清楚。 1…...

编程日记 2023/10/19 19:01:20

从WWDC看苹果产品发展的规律

WWDC 是苹果公司一年一度面向全球开发者的盛会&#xff0c;其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具&#xff0c;对过去十年 WWDC 主题演讲内容进行了系统化分析&#xff0c;形成了这份…...

编程新知 2026/2/2 21:52:33

shell脚本--常见案例

1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件&#xff1a; 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

编程新知 2026/2/7 19:53:11

MFC内存泄露

1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

编程新知 2026/2/10 4:35:17

【入坑系列】TiDB 强制索引在不同库下不生效问题

文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1：执行计划绑定问题？尝试：SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库，并对 SQL 进行优化了，添加了强制索引。 UAT 环境已经生效，但 PROD 环境强制索…...

编程新知 2026/1/31 21:56:58

【大模型RAG】Docker 一键部署 Milvus 完整攻略

本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装&#xff1b;只需暴露 19530&#xff08;gRPC&#xff09;与 9091&#xff08;HTTP/WebUI&#xff09;两个端口&#xff0c;即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

编程新知 2026/1/31 8:08:07

macOS多出来了：Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用

文章目录 问题现象问题原因解决办法 问题现象 macOS启动台&#xff08;Launchpad&#xff09;多出来了&#xff1a;Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显&#xff0c;都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

编程新知 2025/12/4 19:00:05

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表

1、行为树节点分类 在 Nav2（Navigation2）的行为树框架中，行为树节点插件按照功能分为 Action（动作节点）、Condition（条件节点）、Control（控制节点） 和 Decorator（装饰节点） 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务，直接与硬件、传感器或外部系统…...

编程新知 2026/2/7 8:45:41

P3 QT项目----记事本（3.8）

3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

编程新知 2026/2/1 6:56:36

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序

一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

编程新知 2025/11/26 13:15:57

C++ 求圆面积的程序（Program to find area of a circle）

给定半径r&#xff0c;求圆的面积。圆的面积应精确到小数点后5位。 例子&#xff1a; 输入&#xff1a;r 5 输出&#xff1a;78.53982 解释&#xff1a;由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982&#xff0c;因为我们只保留小数点后 5 位数字。 输…...

编程新知 2026/1/31 12:52:15