统计学习方法 隐马尔可夫模型
文章目录
- 统计学习方法 隐马尔可夫模型
- 基本概念
- 概率计算问题
- 直接计算法
- 前向算法
- 后向算法
- 前向概率和后向概率
- 学习问题
- 监督学习算法
- Baum-Welch 算法
- E 步
- M 步
- 参数估计公式
- 算法描述
- 解码问题
- 近似算法
- Viterbi 算法
统计学习方法 隐马尔可夫模型
读李航的《统计学习方法》时,关于隐马尔可夫模型的笔记
隐马尔可夫模型(hidden Markov model, HMM)是可用于标注问题的统计学习模型,属于生成模型。
基本概念
隐马尔可夫模型:在 Markov 链的基础上,随机生成不可观测的状态序列,再由每个状态生成一个观测,产生观测序列,序列的每个位置可看成一个时刻。
隐马尔可夫模型由初始概率分布 π \pi π 、状态转移概率分布 A A A 以及观测概率分布 B B B 确定,符号定义如下:
设 Q Q Q 是所有可能状态的集合, V V V 是所有可能观测的集合:
Q = { q 1 , q 2 , ⋯ , q N } , V = { v 1 , v 2 , ⋯ , v M } Q=\set{q_1,\,q_2,\,\cdots,\,q_N},\quad V=\set{v_1,\,v_2,\,\cdots,\,v_M} Q={q1,q2,⋯,qN},V={v1,v2,⋯,vM}
N N N 是可能的状态数, M M M 是可能的观测数。 I I I 是长度为 T T T 的状态序列, O O O 是对应的观测序列:
I = { i 1 , i 2 , ⋯ , i T } , O = ( o 1 , o 2 , ⋯ , o T ) I=\set{i_1,\,i_2,\,\cdots,\,i_T},\quad O=(o_1,\,o_2,\,\cdots,\,o_T) I={i1,i2,⋯,iT},O=(o1,o2,⋯,oT)
A A A 是状态转移概率矩阵,跟 Markov 链的定义是一样的:
A = [ a i j ] N × N A=[a_{ij}]_{N\times N} A=[aij]N×N
其中 a i j a_{ij} aij 代表从状态 q i q_i qi 转移到状态 q j q_j qj 的概率:
a i j = P ( i t + 1 = q j ∣ i t = q i ) , i = 1 , 2 , ⋯ , N ; j = 1 , 2 , ⋯ , N a_{ij}=P(i_{t+1}=q_j|i_{t}=q_i),\quad i=1,\,2,\,\cdots,\,N;\quad j=1,\,2,\,\cdots,\,N aij=P(it+1=qj∣it=qi),i=1,2,⋯,N;j=1,2,⋯,N
B B B 是观测概率矩阵:
B = [ b j ( k ) ] N × M B=[b_j(k)]_{N\times M} B=[bj(k)]N×M
其中 b j ( k ) b_j(k) bj(k) 代表状态 q j q_j qj 产生观测结果 v k v_k vk 的概率:
b j ( k ) = P ( o t = v k ∣ i t = q j ) , k = 1 , 2 , ⋯ , M ; j = 1 , 2 , ⋯ , N ; b_j(k)=P(o_t=v_k|i_t=q_j),\quad k=1,\,2,\,\cdots,\,M; \quad j=1,\,2,\,\cdots,\,N; bj(k)=P(ot=vk∣it=qj),k=1,2,⋯,M;j=1,2,⋯,N;
π \pi π 是初始概率向量:
π = ( π i ) \pi=(\pi_i) π=(πi)
其中 π i \pi_i πi 代表初始时刻( t = 1 t=1 t=1)处于状态 q i q_i qi 的概率:
π i = P ( i 1 = q i ) , i = 1 , 2 , ⋯ , N \pi_i=P(i_1=q_i),\quad i=1,\,2,\,\cdots,\,N πi=P(i1=qi),i=1,2,⋯,N
即隐马尔可夫模型 λ \lambda λ 可以表示为三元组:
λ = ( π , A , B ) \lambda=(\pi,\,A,\,B) λ=(π,A,B)
隐马尔可夫模型的基本假设:有两个基本假设
- 齐次 Markov 性:任意时刻 t t t 的状态只依赖于前一时刻状态,而与其他时刻的状态及观测无关,与时刻 t t t 也无关:
P ( i t ∣ i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , i = 1 , 2 , ⋯ , T P(i_{t}|i_{t-1},\,o_{t-1},\,\cdots,\,i_1,\,o_1)=P(i_t|i_{t-1}),\quad i=1,\,2,\,\cdots,\,T P(it∣it−1,ot−1,⋯,i1,o1)=P(it∣it−1),i=1,2,⋯,T
- 观测独立性:任意时刻的观测只依赖于该时刻所处的 Markov 链上的状态,与其他任何观测及状态无关:
P ( o t ∣ i T , o T , ⋯ , i t + 1 , o t + 1 , i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( o t ∣ i t ) P(o_t|i_T,\,o_T,\,\cdots,\,i_{t+1},\,o_{t+1},\,i_{t-1},\,o_{t-1},\,\cdots,\,i_1,\,o_1)=P(o_t|i_t) P(ot∣iT,oT,⋯,it+1,ot+1,it−1,ot−1,⋯,i1,o1)=P(ot∣it)
标注问题:对于标注问题,我们可以认为标注问题的数据是由 HMM 生成的,并且状态对应着标记,只要通过学习和预测算法就可以进行标注。
例(盒子和球模型):有四个盒子,每个盒子里装有若干红、白两种颜色的球:
box 1 box 2 box 3 box 4 red ball 5 3 6 8 white ball 5 7 4 2 \begin{array}{ccccc} \hline & \text{box}1 & \text{box}2 & \text{box}3 & \text{box}4 \\ \hline \text{red ball} & 5 & 3 & 6 & 8\\ \hline \text{white ball} & 5 & 7 & 4 & 2\\ \hline \end{array} red ballwhite ballbox155box237box364box482
按照以下抽球方式,产生一个颜色的观测序列:
- 开始时,从四个盒子中等概率地选择一个,有放回地取出一个球并记录颜色;
- 然后转移到下一个盒子:如果是盒子 1,则必转移到盒子 2;如果是盒子 2 或盒子 3,则分别以 0.4 和 0.6 的概率转移到左边和右边的盒子;如果是盒子 4,则各以 0.5 的概率留在盒子 4 或转移到盒子 3;
- 重复,比如进行 5 次,得到一个观测序列:
O = { r , r , w , w , r } O=\set{r,\,r,\,w,\,w,\,r} O={r,r,w,w,r}
这个过程中,观察者只能观测到球的颜色,而并不知道球是从哪个盒子里取出的。因此盒子对应状态,即:
Q = { 1 , 2 , 3 , 4 } , N = 4 Q=\set{1,\,2,\,3,\,4},\quad N=4 Q={1,2,3,4},N=4
球的颜色为观测集合:
V = { r , w } , M = 2 V=\set{r,\,w},\quad M=2 V={r,w},M=2
初始概率分布为:
π = ( 0.25 , 0.25 , 0.25 , 0.25 ) T \pi=(0.25,\,0.25,\,0.25,\,0.25)^T π=(0.25,0.25,0.25,0.25)T
状态转移概率分布为:
A = [ 0 1 0 0 0.4 0 0.6 0 0 0.4 0 0.6 0 0 0.5 0.5 ] A=\begin{bmatrix} 0 & 1 & 0 & 0 \\ 0.4 & 0 & 0.6 & 0 \\ 0 & 0.4 & 0 & 0.6 \\ 0 & 0 & 0.5 & 0.5 \\ \end{bmatrix} A= 00.400100.4000.600.5000.60.5
观测概率分布为:
B = [ 0.5 0.5 0.3 0.7 0.6 0.4 0.8 0.2 ] B=\begin{bmatrix} 0.5 & 0.5 \\ 0.3 & 0.7\\ 0.6 & 0.4\\ 0.8 & 0.2 \\ \end{bmatrix} B= 0.50.30.60.80.50.70.40.2
三个基本问题:给定 HMM,随机生成一个观测序列是很容易的。但还有以下三个不那么明显的问题:
- 概率计算问题:给定模型和观测序列,计算该模型产生该观测序列的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) ;
- 学习问题:给定观测序列,估计模型参数,使得 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) 最大,即用极大似然估计的方法估计参数;
- 预测问题:也称解码问题,已知模型参数和观测序列,求使得条件概率 P ( I ∣ O ) P(I|O) P(I∣O) 最大的状态序列 I = ( i 1 , i 2 , ⋯ , i T ) I=(i_1,\,i_2,\,\cdots,\,i_T) I=(i1,i2,⋯,iT) ,即给定观测序列,求出最有可能的对应的状态序列。
概率计算问题
概率计算问题是指,给定模型和观测序列,计算该模型产生该观测序列的概率。
直接计算法
算法:直接枚举所有可能的长度为 T T T 的状态序列,然后求出各状态序列产生该观测序列的概率,最后求和。
出现状态序列 I = ( i 1 , i 2 , ⋯ , i T ) I=(i_1,\,i_2,\,\cdots,\,i_T) I=(i1,i2,⋯,iT) 的概率为:
P ( I ∣ λ ) = π i 1 a i 1 i 2 a i 2 i 3 ⋯ a i T − 1 i T P(I|\lambda)=\pi_{i_1}a_{i_1i_2}a_{i_2i_3}\cdots a_{i_{T-1}i_T} P(I∣λ)=πi1ai1i2ai2i3⋯aiT−1iT
对于该状态序列,产生观测 O = ( o 1 , o 2 , ⋯ o T ) O=(o_1,\,o_2,\,\cdots o_T) O=(o1,o2,⋯oT) 的概率为:
P ( O ∣ I , λ ) = b i 1 ( o 1 ) b i 2 ( o 2 ) ⋯ b i T ( o T ) P(O|I,\,\lambda)=b_{i_1}(o_1)b_{i_2}(o_2)\cdots b_{i_T}(o_T) P(O∣I,λ)=bi1(o1)bi2(o2)⋯biT(oT)
则该观测序列出现的总的概率为:
P ( O ∣ λ ) = ∑ I P ( O ∣ I , λ ) P ( I ∣ λ ) = ∑ i 1 , i 2 , ⋯ , i T π i 1 b i 1 ( o 1 ) a i 1 i 2 b i 2 ( o 2 ) a i 2 i 3 ⋯ a i T − 1 i T b i T ( o T ) \begin{aligned} P(O|\lambda)=&\, \sum_I P(O|I,\,\lambda)P(I|\lambda) \\ =&\, \sum_{i_1,\,i_2,\,\cdots,\,i_T}\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)a_{i_2i_3}\cdots a_{i_{T-1}i_T}b_{i_T}(o_T) \end{aligned} P(O∣λ)==I∑P(O∣I,λ)P(I∣λ)i1,i2,⋯,iT∑πi1bi1(o1)ai1i2bi2(o2)ai2i3⋯aiT−1iTbiT(oT)
但是这个算法的时间复杂度为 O ( T N T ) O(TN^T) O(TNT) ,是指数级别的。
前向算法
前向概率:给定模型 λ \lambda λ ,定义前向概率为,到时刻 t t t 时,前面出现的观测序列为 O [ 0 , t ] = ( 0 1 , o 2 , ⋯ , o t ) O[0,\,t]=(0_1,\,o_2,\,\cdots,\,o_t) O[0,t]=(01,o2,⋯,ot) ,而此时状态正好为 q i q_i qi 的概率,记为:
α t ( i ) = P ( o 1 , o 2 , ⋯ , o t , i t = q t ∣ λ ) \alpha_t(i)=P(o_1,\,o_2,\,\cdots,\,o_t,\,i_t=q_t|\lambda) αt(i)=P(o1,o2,⋯,ot,it=qt∣λ)
可以想到,如果知道了前一时刻 t − 1 t-1 t−1 所有状态的前向概率,则可以得到下一时刻 t t t 任一状态 q i q_i qi 的前向概率,只需要前向概率乘以状态转移概率,再乘以产生 o t o_t ot 的概率,最后求和即可:
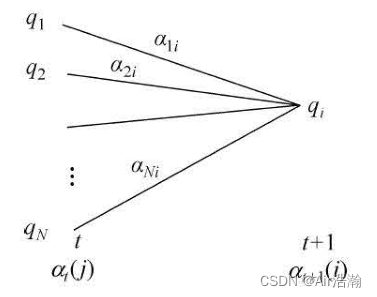
并且,知道了 T T T 时刻所有状态的前向概率以后,将所有状态的前向概率求和即可得到
算法:观测序列概率的前向算法
- 输入:HMM λ \lambda λ ,观测序列 O O O ;
- 输出:产生该观测序列的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) ;
- 初值:
α 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , ⋯ , N \alpha_1(i)=\pi_ib_i(o_1),\quad i=1,\,2,\,\cdots,\,N α1(i)=πibi(o1),i=1,2,⋯,N
- 递推:对于 t = 1 , 2 , ⋯ , T − 1 t=1,\,2,\,\cdots,\,T-1 t=1,2,⋯,T−1 ,递推地计算后一时刻的前向概率:
α t + 1 ( i ) = b i ( o t + 1 ) ∑ j = 1 N α t ( j ) a j i \alpha_{t+1}(i)=b_i(o_{t+1})\sum_{j=1}^{N}\alpha_t(j)a_{ji} αt+1(i)=bi(ot+1)j=1∑Nαt(j)aji
- 终止:求 T T T 时刻所有状态的前向概率的和:
P ( O ∣ λ ) = ∑ 1 N α T ( i ) P(O|\lambda)= \sum_{1}^{N} \alpha_T(i) P(O∣λ)=1∑NαT(i)
整个计算过程即如下的 DAG(有点像 Bellman-Ford 的计算路径),想象一下,其实直接算法的计算路径就如同一颗以状态数 N N N 为子节点数的 N N N 叉树,而前向算法则是将每一层重复节点进行了合并(就如同 DP 优化暴力算法一样),因此得到的时间复杂度为 O ( N 2 T ) O(N^2T) O(N2T) :
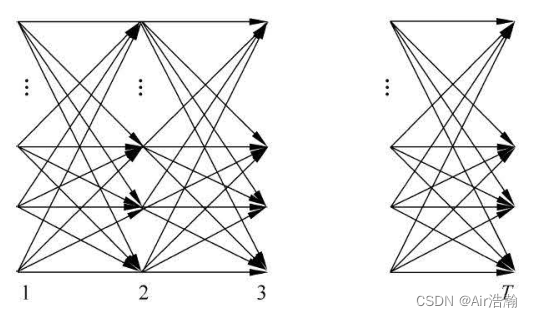
例(盒子和球模型):状态集合为 Q = { 1 , 2 , 3 } Q=\set{1,\,2,\,3} Q={1,2,3},观测集合为 V = { r , w } V=\set{r,\,w} V={r,w} ,
A = [ 0.5 0.2 0.3 0.3 0.5 0.2 0.2 0.3 0.5 ] B = [ 0.5 0.5 0.4 0.6 0.7 0.3 ] π = [ 0.2 0.4 0.4 ] A=\begin{bmatrix} 0.5 & 0.2 & 0.3\\ 0.3 & 0.5 & 0.2\\ 0.2 & 0.3 & 0.5\\ \end{bmatrix} \quad B=\begin{bmatrix} 0.5 & 0.5 \\ 0.4 & 0.6\\ 0.7 & 0.3\\ \end{bmatrix} \quad \pi=\begin{bmatrix} 0.2\\ 0.4\\ 0.4\\ \end{bmatrix} A= 0.50.30.20.20.50.30.30.20.5 B= 0.50.40.70.50.60.3 π= 0.20.40.4
假设得到的观测序列为 O = ( r , w , r ) O=(r,\,w,\,r) O=(r,w,r) ,则前向概率为:
T 1 2 3 box 1 0.10 0.077 0.04187 box 2 0.16 0.1104 0.03551 box 3 0.28 0.0606 0.05284 \begin{array}{cccc} \hline T & 1 & 2 & 3 \\ \hline \text{box}1 & 0.10 & 0.077 & 0.04187 \\ \hline \text{box}2 & 0.16 & 0.1104 & 0.03551\\ \hline \text{box}3 & 0.28 & 0.0606 & 0.05284 \\ \hline \end{array} Tbox1box2box310.100.160.2820.0770.11040.060630.041870.035510.05284
这个表格的计算顺序是一列一列计算的,最后一列的和即为所求结果:
P ( O ∣ λ ) = 0.13022 P(O|\lambda)=0.13022 P(O∣λ)=0.13022
后向算法
后向概率:给定模型 λ \lambda λ ,后向概率定义为,时刻 t t t 为状态 q i q_i qi 的条件下,后续的观测序列正好是 O [ t + 1 , T ] = ( o t + 1 , o t + 2 , ⋯ , o T ) O[t+1,\,T]=(o_{t+1},\,o_{t+2},\,\cdots,\,o_{T}) O[t+1,T]=(ot+1,ot+2,⋯,oT) 的概率:
β t ( i ) = P ( o t + 1 , o t + 1 , ⋯ , o T ∣ i t = q i , λ ) \beta_t(i)=P(o_{t+1},\,o_{t+1},\,\cdots,\,o_T|i_t=q_i,\,\lambda) βt(i)=P(ot+1,ot+1,⋯,oT∣it=qi,λ)
可以想到,如果知道 t + 1 t+1 t+1 时刻所有状态的后向概率,那么就可以求得 t t t 时刻任一状态的后向概率,只需要将后向概率乘以状态转移概率,再乘上产生观测为 o t + 1 o_{t+1} ot+1 的概率,最后求和即可:
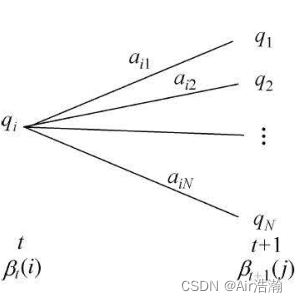
注意:后向概率 β t ( i ) \beta_t(i) βt(i) 中并没有包含 t t t 时刻的观测 o t o_t ot 出现的概率。
算法:观测序列概率的后向算法
- 输入:HMM λ \lambda λ ,观测序列 O O O ;
- 输出:产生该观测序列的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) ;
- 初值:时刻 T T T 以后没有观测了,所以可以认为处于每个状态的后向概率是 1:
β T ( i ) = 1 , i = 1 , 2 , ⋯ , N \beta_T(i)=1,\quad i=1,\,2,\,\cdots,\,N βT(i)=1,i=1,2,⋯,N
- 递归:对于 t = T − 1 , T − 2 , ⋯ , 1 t=T-1,\,T-2,\,\cdots,\,1 t=T−1,T−2,⋯,1 递归地计算前一时刻的后向概率:
β t ( i ) = ∑ j = 1 N a i j b j ( o t + 1 ) β t + 1 ( j ) , i = 1 , 2 , ⋯ , N \beta_t(i)=\sum_{j=1}^{N}a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j),\quad i=1,\,2,\,\cdots,\,N βt(i)=j=1∑Naijbj(ot+1)βt+1(j),i=1,2,⋯,N
- 求和:最后时刻 t = 1 t=1 t=1 时,后向概率要乘以初始分布位于该状态的概率,以及产生第一个观测的概率,并求和:
P ( O ∣ λ ) = ∑ i = 1 N π i b i β 1 ( i ) P(O|\lambda)=\sum_{i=1}^{N}\pi_ib_i\beta_{1}(i) P(O∣λ)=i=1∑Nπibiβ1(i)
前向概率和后向概率
状态转移的过程可以看成是如下图的某条路径:

经过某个点的概率:利用前向和后向概率的定义,可以将观测序列概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) 统一写成:
P ( O ∣ λ ) = ∑ j = 1 N α t ( j ) β t ( j ) , t = 1 , 2 , ⋯ , T − 1 P(O|\lambda)=\sum\limits_{j=1}^N \alpha_t(j)\beta_t(j),\quad t=1,\,2,\,\cdots,\,T-1 P(O∣λ)=j=1∑Nαt(j)βt(j),t=1,2,⋯,T−1
可以理解成,我们任意选择其中一层,其中共有 N N N 个节点。对于每个节点, a t ( i ) a_t(i) at(i) 代表产生前面的观测序列后到达该节点的概率, β t ( j ) \beta_{t}(j) βt(j) 代表从该节点出发得到剩余的观测序列的概率。所有这些乘在一起则代表:给定模型 λ \lambda λ ,在 t t t 时刻正好经过该节点并且最终也正好得到 O O O 的概率
即:
P ( i t = q i , O ∣ λ ) = α t ( j ) β t ( j ) P(i_t=q_i,\,O|\lambda)=\alpha_t(j)\beta_t(j) P(it=qi,O∣λ)=αt(j)βt(j)
而给定模型 λ \lambda λ 和观测序列 O O O ,在时刻 t t t 处于状态 q i q_i qi 的概率,记为:
γ t ( i ) = P ( i t = q i ∣ O , λ ) = P ( i t = q i , O ∣ λ ) P ( O ∣ λ ) = α t ( j ) β t ( j ) ∑ j = 1 N α t ( j ) β t ( j ) \begin{aligned} \gamma_t(i)=&\, P(i_t=q_i|O,\,\lambda) \\ =&\ \frac{P(i_t=q_i,\,O|\lambda)}{P(O|\lambda)} \\ =&\, \frac{\alpha_t(j)\beta_t(j)}{\sum\limits_{j=1}^N \alpha_t(j)\beta_t(j)} \end{aligned} γt(i)===P(it=qi∣O,λ) P(O∣λ)P(it=qi,O∣λ)j=1∑Nαt(j)βt(j)αt(j)βt(j)
经过某条边的概率:利用前向和后向概率的定义,可以将观测序列概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) 统一写成:
P ( O ∣ λ ) = ∑ i = 1 N ∑ j = 1 N a t ( i ) a i j b j ( o t + 1 ) β t + 1 ( j ) , t = 1 , 2 , ⋯ , T − 1 P(O|\lambda)=\sum_{i=1}^{N}\sum_{j=1}^{N} a_t(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j),\quad t=1,\,2,\,\cdots,\,T-1 P(O∣λ)=i=1∑Nj=1∑Nat(i)aijbj(ot+1)βt+1(j),t=1,2,⋯,T−1
可以理解成,我们任意选择相邻的某两层节点,其中共有 N 2 N^2 N2 条边。对于每条边, a t ( i ) a_t(i) at(i) 代表产生前面的观测序列后到达左节点的概率, a i j a_{ij} aij 代表从左节点转移到右节点的概率, b j ( o t + 1 ) β t + 1 ( j ) b_{j}(o_{t+1})\beta_{t+1}(j) bj(ot+1)βt+1(j) 代表从右节点出发得到剩余的观测序列的概率。所有这些乘在一起则代表:给定模型 λ \lambda λ ,在 t → t + 1 t\to t+1 t→t+1 时刻正好经过这条边并且最终也正好得到 O O O 的概率,即:
P ( i t = q i , i t + 1 = q j , O ∣ λ ) = a t ( i ) a i j b j ( o t + 1 ) β t + 1 ( j ) P(i_t=q_i,\,i_{t+1}=q_{j},\,O|\lambda)=a_t(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j) P(it=qi,it+1=qj,O∣λ)=at(i)aijbj(ot+1)βt+1(j)
对相邻的某两层节点之间所有边,将经过每条边的概率求和,即得到 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) 。
而给定模型 λ \lambda λ 和观测序列 O O O , 在 t → t + 1 t\to t+1 t→t+1 时刻正好经过某条边的概率为:
ξ t ( i , j ) = P ( i t = q i , i t + 1 = q j ∣ O , λ ) = P ( i t = q i , i t + 1 = q j , O ∣ λ ) P ( O ∣ λ ) = a t ( i ) a i j b j ( o t + 1 ) β t + 1 ( j ) ∑ i = 1 N ∑ j = 1 N a t ( i ) a i j b j ( o t + 1 ) β t + 1 ( j ) \begin{aligned} \xi_t(i,\,j)=&\, P(i_t=q_i,\,i_{t+1}=q_j|O,\,\lambda) \\ =&\, \frac{P(i_t=q_i,\,i_{t+1}=q_j,\,O|\lambda)}{P(O|\lambda)} \\ =&\, \frac{a_t(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)}{\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N} a_t(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)} \end{aligned} ξt(i,j)===P(it=qi,it+1=qj∣O,λ)P(O∣λ)P(it=qi,it+1=qj,O∣λ)i=1∑Nj=1∑Nat(i)aijbj(ot+1)βt+1(j)at(i)aijbj(ot+1)βt+1(j)
学习问题
学习问题是指,给定观测序列,估计模型参数,使得 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) 最大,即用极大似然估计的方法估计参数。
监督学习算法
就是使用完全数据,假设训练数据包含 S S S 个长度相同的观测序列和对应的状态序列,那么可以使用极大似然估计法来估计 HMM 的参数:
train_data = { ( O 1 , I 1 ) , ( O 1 , I 2 ) , ⋯ , ( O S , I S ) } \text{train\_data}=\set{(O_1,\,I_1),\,(O_1,\,I_2),\,\cdots,\,(O_S,\,I_S)} train_data={(O1,I1),(O1,I2),⋯,(OS,IS)}
- 转移概率 a i j a_{ij} aij 的估计:就是从状态 q i q_i qi 出发的转移中,转移到 q j q_j qj 的频率;设样本中从状态 q i q_i qi 转移到状态 q j q_j qj 的频数为 A i j A_{ij} Aij ,则状态转移概率 a i j a_{ij} aij 的估计是:
a ^ i j = A i j ∑ j = 1 N A i j , i = 1 , 2 , ⋯ , N ; j = 1 , 2 , ⋯ , N \hat{a}_{ij}=\frac{A_{ij}}{\sum\limits_{j=1}^N A_{ij}},\quad i=1,\,2,\,\cdots,\,N;\quad j=1,\,2,\,\cdots,\,N a^ij=j=1∑NAijAij,i=1,2,⋯,N;j=1,2,⋯,N
- 观测概率 b j ( k ) b_j(k) bj(k) 的估计:就是处于状态 q j q_j qj 时,产生观测 v k v_k vk 的频率;设样本中处于状态 q j q_j qj 时,产生观测 v k v_k vk 的频数为 B j k B_{jk} Bjk ,则观测概率 b j ( k ) b_j(k) bj(k) 的估计为:
b ^ j ( k ) = B j k ∑ k = 1 M B j k , j = 1 , 2 , ⋯ , N ; k = 1 , 2 , ⋯ , M \hat{b}_j(k)=\frac{B_{jk}}{\sum\limits_{k=1}^{M}B_{jk}},\quad j=1,\,2,\,\cdots,\,N; \quad k=1,\,2,\,\cdots,\,M b^j(k)=k=1∑MBjkBjk,j=1,2,⋯,N;k=1,2,⋯,M
- 初始状态概率 π i \pi_i πi 的估计:就是 S S S 个样本中初始状态为 q i q_i qi 的频率;
Baum-Welch 算法
Baum-Welch 算法是 EM 算法在 HMM 的参数估计中的具体实现。
E 步
这里 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,\,o_2,\,\cdots,\,o_T) O=(o1,o2,⋯,oT) 相当于 EM 算法中的 Y Y Y , I = ( i 1 , i 2 , ⋯ , i T ) I=(i_1,\,i_2,\,\cdots,\,i_T) I=(i1,i2,⋯,iT) 相当于 EM 算法中的 Z Z Z ,而 λ = ( π , A , B ) \lambda=(\pi,\,A,\,B) λ=(π,A,B) 相当于 EM 算法中的 θ \theta θ 。因此,完全数据的对数似然函数为:
log P ( O , I ∣ λ ) \log P(O,\,I|\lambda) logP(O,I∣λ)
Q Q Q 函数为:
Q ( λ ∣ λ ^ ) = E I [ log P ( O , I ∣ λ ) ∣ O , λ ^ ] = ∑ I log P ( O , I ∣ λ ) P ( I ∣ λ ^ ) = ∑ I log P ( O , I ∣ λ ) P ( O , I ∣ λ ^ ) P ( O ∣ λ ^ ) \begin{aligned} Q(\lambda|\hat\lambda) =&\, E_I[\log P(O,\,I|\lambda)|O,\,\hat\lambda]\\ =&\, \sum_I \log P(O,\,I|\lambda)P(I|\hat\lambda) \\ =&\, \sum_I \log P(O,\,I|\lambda)\frac{P(O,\,I|\hat\lambda)}{P(O|\hat\lambda)} \end{aligned} Q(λ∣λ^)===EI[logP(O,I∣λ)∣O,λ^]I∑logP(O,I∣λ)P(I∣λ^)I∑logP(O,I∣λ)P(O∣λ^)P(O,I∣λ^)
因为 Q Q Q 函数的变量为 λ \lambda λ , 1 P ( O ∣ λ ^ ) \frac{1}{P(O|\hat\lambda)} P(O∣λ^)1 对于 Q Q Q 函数来说是个常数,不影响极值的求解,因此我们将其省去,得到:
Q ( λ ∣ λ ^ ) = ∑ I log P ( O , I ∣ λ ) P ( O , I ∣ λ ^ ) Q(\lambda|\hat\lambda)=\sum_I \log P(O,\,I|\lambda)P(O,\,I|\hat\lambda) Q(λ∣λ^)=I∑logP(O,I∣λ)P(O,I∣λ^)
而:
P ( O , I ∣ λ ) = π i 1 b i 1 ( o 1 ) a i 1 i 2 ⋯ a i T − 1 i T b i T ( o T ) P(O,\,I|\lambda)=\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}\cdots a_{i_{T-1}i_T}b_{i_T}(o_T) P(O,I∣λ)=πi1bi1(o1)ai1i2⋯aiT−1iTbiT(oT)
因此 Q Q Q 函数可以写成:
Q ( λ ∣ λ ^ ) = ∑ I log π i 1 P ( O , I ∣ λ ^ ) + ∑ I ( ∑ t = 1 T − 1 log a i t i t + 1 ) P ( O , I ∣ λ ^ ) + ∑ I ( ∑ t = 1 T log b i t ( o t ) ) P ( O , I ∣ λ ^ ) \begin{aligned} Q(\lambda|\hat\lambda) =&\, \sum_I\log\pi_{i_1}P(O,I|\hat\lambda) \\ +&\, \sum_I\left( \sum_{t=1}^{T-1} \log a_{i_ti_{t+1}} \right)P(O,I|\hat\lambda) \\ +&\, \sum_I\left( \sum_{t=1}^{T} \log b_{i_t}(o_t) \right)P(O,I|\hat\lambda) \end{aligned} Q(λ∣λ^)=++I∑logπi1P(O,I∣λ^)I∑(t=1∑T−1logaitit+1)P(O,I∣λ^)I∑(t=1∑Tlogbit(ot))P(O,I∣λ^)
M 步
由于 π i \pi_i πi 、 a i j a_{ij} aij 和 b j ( k ) b_j(k) bj(k) 分别出现在 Q Q Q 函数的三项中,因此只需要对各项分别极大化:
- 求 π i \pi_i πi 极值点:可以进行一些变换,使用了类似于导出三硬币的 EM 算法时的技巧:
∑ I log π i 1 P ( O , I ∣ λ ^ ) = ∑ i 1 ∑ i t , t ≠ 1 log π i 1 P ( O , I ∣ λ ^ ) \begin{aligned} \sum_I\log\pi_{i_1}P(O,I|\hat\lambda) =&\, \sum_{i_1}\sum_{i_t,\,t\not=1}\log \pi_{i_1}P(O,I|\hat\lambda) \end{aligned} I∑logπi1P(O,I∣λ^)=i1∑it,t=1∑logπi1P(O,I∣λ^)
注意到在固定 i 1 i_1 i1 的取值时,有:
∑ i t , t ≠ 1 log π i 1 P ( O , I ∣ λ ^ ) = log π i 1 ∑ i t , t ≠ 1 P ( O , I ∣ λ ^ ) = log π i 1 P ( O , i 1 = i 1 ∣ λ ^ ) \sum_{i_t,\,t\not=1}\log \pi_{i_1}P(O,I|\hat\lambda)=\log \pi_{i_1}\sum_{i_t,\,t\not=1}P(O,I|\hat\lambda)=\log \pi_{i_1}P(O,i_1=i_1|\hat\lambda) it,t=1∑logπi1P(O,I∣λ^)=logπi1it,t=1∑P(O,I∣λ^)=logπi1P(O,i1=i1∣λ^)
P ( O , i 1 = i 1 ∣ λ ^ ) P(O,i_1=i_1|\hat\lambda) P(O,i1=i1∣λ^) 这个记号写得不好。。。其实就是代表给定参数 λ ^ \hat\lambda λ^ 的情况下,得到观测 O O O 并且第一个状态正好是刚刚固定的 i 1 i_1 i1 的概率。因此:
∑ I log π i 1 P ( O , I ∣ λ ^ ) = ∑ i = 1 N log π i P ( O , i 1 = q i ∣ λ ^ ) \sum_I\log\pi_{i_1}P(O,I|\hat\lambda)=\sum_{i=1}^{N}\log\pi_{i}P(O,i_1=q_i|\hat\lambda) I∑logπi1P(O,I∣λ^)=i=1∑NlogπiP(O,i1=qi∣λ^)
这里 π i \pi_i πi 满足约束条件 ∑ i = 1 N π i = 1 \sum\limits_{i=1}^{N}\pi_i=1 i=1∑Nπi=1 ,使用 Lagrange 乘子法,Lagrangian 为:
L ( π ) = ∑ i = 1 N log π i P ( O , i 1 = q i ∣ λ ^ ) − γ ( 1 − ∑ i = 1 N π i ) L(\pi)=\sum_{i=1}^{N}\log\pi_{i}P(O,i_1=q_i|\hat\lambda)-\gamma(1-\sum\limits_{i=1}^{N}\pi_i) L(π)=i=1∑NlogπiP(O,i1=qi∣λ^)−γ(1−i=1∑Nπi)
FOC 为:
∂ L ( π ) ∂ π i = P ( O , i 1 = q i ∣ λ ^ ) π i + γ = 0 ⇒ P ( O , i 1 = q i ∣ λ ^ ) + π i γ = 0 \begin{aligned} \frac{\partial L(\pi)}{\partial \pi_i} =&\,\frac{P(O,i_1=q_i|\hat\lambda)}{\pi_i}+\gamma=0 \\ \Rightarrow&\, P(O,i_1=q_i|\hat\lambda)+\pi_i\gamma=0 \end{aligned} ∂πi∂L(π)=⇒πiP(O,i1=qi∣λ^)+γ=0P(O,i1=qi∣λ^)+πiγ=0
对所有 FOC 求和,解得 γ \gamma γ 为:
γ = − ∑ i = 1 N P ( O , i 1 = q i ∣ λ ^ ) = − P ( O ∣ λ ^ ) \gamma=-\sum_{i=1}^{N}P(O,i_1=q_i|\hat\lambda)=-P(O|\hat\lambda) γ=−i=1∑NP(O,i1=qi∣λ^)=−P(O∣λ^)
代回解得:
π i = P ( O , i 1 = q i ∣ λ ^ ) P ( O ∣ λ ^ ) \pi_i=\frac{P(O,i_1=q_i|\hat\lambda)}{P(O|\hat\lambda)} πi=P(O∣λ^)P(O,i1=qi∣λ^)
这实际上就是给定参数 λ ^ \hat\lambda λ^ 和观测 O O O ,1 时刻经过状态 q i q_i qi 的概率。
- 求 a i j a_{ij} aij 极值点:同样地,对目标函数进行一些变换:
∑ I ( ∑ t = 1 T − 1 log a i t i t + 1 ) P ( O , I ∣ λ ^ ) = ∑ I ∑ t = 1 T − 1 log a i t i t + 1 P ( O , I ∣ λ ^ ) (因为 P ( O , I ∣ λ ^ ) 与 t 无关) = ∑ t = 1 T − 1 ∑ I log a i t i t + 1 P ( O , I ∣ λ ^ ) (可以交换求和顺序) = ∑ t = 1 T − 1 ∑ i t ∑ i t + 1 ∑ i else log a i t i t + 1 P ( O , I ∣ λ ^ ) = ∑ t = 1 T − 1 ∑ i t ∑ i t + 1 log a i t i t + 1 ∑ i else P ( O , I ∣ λ ^ ) (因为 log a i t i t + 1 与 i else 无关) = ∑ t = 1 T − 1 ∑ i = 1 N ∑ j = 1 N log a i j P ( O , i t = q i , i t + 1 = q j ∣ λ ^ ) = ∑ i = 1 N ∑ j = 1 N ∑ t = 1 T − 1 log a i j P ( O , i t = q i , i t + 1 = q j ∣ λ ^ ) (可以交换求和顺序) \begin{aligned} &\, \sum_I\left( \sum_{t=1}^{T-1} \log a_{i_ti_{t+1}} \right)P(O,I|\hat\lambda) \\ =&\, \sum_I \sum_{t=1}^{T-1} \log a_{i_ti_{t+1}} P(O,I|\hat\lambda) \quad\text{(因为$P(O,I|\hat\lambda)$与$t$无关)} \\ =&\, \sum_{t=1}^{T-1}\sum_I \log a_{i_ti_{t+1}} P(O,I|\hat\lambda) \quad\text{(可以交换求和顺序)} \\ =&\, \sum_{t=1}^{T-1}\sum_{i_t}\sum_{i_{t+1}}\sum_{i_\text{else}}\log a_{i_ti_{t+1}} P(O,I|\hat\lambda) \\ =&\, \sum_{t=1}^{T-1}\sum_{i_t}\sum_{i_{t+1}}\log a_{i_ti_{t+1}}\sum_{i_\text{else}} P(O,I|\hat\lambda) \quad\text{(因为$\log a_{i_ti_{t+1}}$与$i_\text{else}$无关)} \\ =&\, \sum_{t=1}^{T-1}\sum_{i=1}^{N}\sum_{j=1}^{N}\log a_{ij} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda) \\ =&\, \sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{t=1}^{T-1}\log a_{ij} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda) \quad\text{(可以交换求和顺序)} \\ \end{aligned} ======I∑(t=1∑T−1logaitit+1)P(O,I∣λ^)I∑t=1∑T−1logaitit+1P(O,I∣λ^)(因为P(O,I∣λ^)与t无关)t=1∑T−1I∑logaitit+1P(O,I∣λ^)(可以交换求和顺序)t=1∑T−1it∑it+1∑ielse∑logaitit+1P(O,I∣λ^)t=1∑T−1it∑it+1∑logaitit+1ielse∑P(O,I∣λ^)(因为logaitit+1与ielse无关)t=1∑T−1i=1∑Nj=1∑NlogaijP(O,it=qi,it+1=qj∣λ^)i=1∑Nj=1∑Nt=1∑T−1logaijP(O,it=qi,it+1=qj∣λ^)(可以交换求和顺序)
约束条件同样是 ∑ j = 1 N a i j = 1 \sum\limits_{j=1}^{N}a_{ij}=1 j=1∑Naij=1 ,Lagrangian 为:
L ( a ) = ∑ i = 1 N ∑ j = 1 N ∑ t = 1 T − 1 log a i j P ( O , i t = q i , i t + 1 = q j ∣ λ ^ ) − ∑ i = 1 N γ i ( 1 − ∑ j = 1 N a i j ) L(a)=\sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{t=1}^{T-1}\log a_{ij} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda)-\sum\limits_{i=1}^{N}\gamma_i(1-\sum\limits_{j=1}^{N}a_{ij}) L(a)=i=1∑Nj=1∑Nt=1∑T−1logaijP(O,it=qi,it+1=qj∣λ^)−i=1∑Nγi(1−j=1∑Naij)
FOC 为:
∂ L ( a ) ∂ a i j = ∑ t = 1 T − 1 P ( O , i t = q i , i t + 1 = q j ∣ λ ^ ) a i j + γ i = 0 ⇒ ∑ t = 1 T − 1 P ( O , i t = q i , i t + 1 = q j ∣ λ ^ ) + a i j γ i = 0 \begin{aligned} \frac{\partial L(a)}{\partial a_{ij}} =&\, \frac{\sum\limits_{t=1}^{T-1} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda)}{a_{ij}}+\gamma_i=0 \\ \Rightarrow &\, \sum\limits_{t=1}^{T-1} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda)+a_{ij}\gamma_i=0 \end{aligned} ∂aij∂L(a)=⇒aijt=1∑T−1P(O,it=qi,it+1=qj∣λ^)+γi=0t=1∑T−1P(O,it=qi,it+1=qj∣λ^)+aijγi=0
将所有 i i i 相同的 FOC 相加,得到:
γ i = − ∑ t = 1 T − 1 P ( O , i t = q i ∣ λ ^ ) \gamma_i=-\sum\limits_{t=1}^{T-1}P(O,i_t=q_i|\hat\lambda) γi=−t=1∑T−1P(O,it=qi∣λ^)
代回解得:
a i j = ∑ t = 1 T − 1 P ( O , i t = q i , i t + 1 = q j ∣ λ ^ ) ∑ t = 1 T − 1 P ( O , i t = q i ∣ λ ^ ) a_{ij}=\frac{\sum\limits_{t=1}^{T-1} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda)}{\sum\limits_{t=1}^{T-1}P(O,i_t=q_i|\hat\lambda)} aij=t=1∑T−1P(O,it=qi∣λ^)t=1∑T−1P(O,it=qi,it+1=qj∣λ^)
- 求 b j ( k ) b_{j}(k) bj(k) 极值点:同样地,对目标函数进行一些变换:
∑ I ( ∑ t = 1 T log b i t ( o t ) ) P ( O , I ∣ λ ^ ) = ∑ I ∑ t = 1 T log b i t ( o t ) P ( O , I ∣ λ ^ ) (因为 P ( O , I ∣ λ ^ ) 与 t 无关) = ∑ t = 1 T ∑ I log b i t ( o t ) P ( O , I ∣ λ ^ ) (可以交换求和顺序) = ∑ t = 1 T ∑ i t ∑ i else log b i t ( o t ) P ( O , I ∣ λ ^ ) = ∑ t = 1 T ∑ i t log b i t ( o t ) ∑ i else P ( O , I ∣ λ ^ ) (因为 log b i t ( o t ) 与 i else 无关) = ∑ t = 1 T ∑ j = 1 N log b j ( o t ) P ( O , i t = q j ∣ λ ^ ) = ∑ j = 1 N ∑ t = 1 T log b j ( o t ) P ( O , i t = q j ∣ λ ^ ) \begin{aligned} &\, \sum_I\left( \sum_{t=1}^{T} \log b_{i_t}(o_t) \right)P(O,I|\hat\lambda) \\ =&\, \sum_I \sum_{t=1}^{T} \log b_{i_t}(o_t)P(O,I|\hat\lambda)\quad\text{(因为$P(O,I|\hat\lambda)$与$t$无关)} \\ =&\, \sum_{t=1}^{T}\sum_I \log b_{i_t}(o_t)P(O,I|\hat\lambda)\quad\text{(可以交换求和顺序)} \\ =&\, \sum_{t=1}^{T}\sum_{i_t}\sum_{i_\text{else}}\log b_{i_t}(o_t)P(O,I|\hat\lambda) \\ =&\, \sum_{t=1}^{T}\sum_{i_t}\log b_{i_t}(o_t)\sum_{i_\text{else}}P(O,I|\hat\lambda)\quad\text{(因为$\log b_{i_t}(o_t)$与$i_\text{else}$无关)} \\ =&\, \sum_{t=1}^{T}\sum\limits_{j=1}^{N}\log b_j(o_t)P(O,i_t=q_j|\hat\lambda) \\ =&\, \sum\limits_{j=1}^{N}\sum_{t=1}^{T}\log b_j(o_t)P(O,i_t=q_j|\hat\lambda) \end{aligned} ======I∑(t=1∑Tlogbit(ot))P(O,I∣λ^)I∑t=1∑Tlogbit(ot)P(O,I∣λ^)(因为P(O,I∣λ^)与t无关)t=1∑TI∑logbit(ot)P(O,I∣λ^)(可以交换求和顺序)t=1∑Tit∑ielse∑logbit(ot)P(O,I∣λ^)t=1∑Tit∑logbit(ot)ielse∑P(O,I∣λ^)(因为logbit(ot)与ielse无关)t=1∑Tj=1∑Nlogbj(ot)P(O,it=qj∣λ^)j=1∑Nt=1∑Tlogbj(ot)P(O,it=qj∣λ^)
约束条件为 ∑ k = 1 M b i ( k ) = 1 \sum\limits_{k=1}^{M}b_{i}(k)=1 k=1∑Mbi(k)=1 ,Lagrangian 为:
L ( b ) = ∑ j = 1 N ∑ t = 1 T log b j ( o t ) P ( O , i t = q j ∣ λ ^ ) − ∑ j = 1 N γ j ( 1 − ∑ k = 1 M b i ( k ) ) L(b)=\sum\limits_{j=1}^{N}\sum_{t=1}^{T}\log b_j(o_t)P(O,i_t=q_j|\hat\lambda)-\sum_{j=1}^{N}\gamma_j(1-\sum\limits_{k=1}^{M}b_{i}(k)) L(b)=j=1∑Nt=1∑Tlogbj(ot)P(O,it=qj∣λ^)−j=1∑Nγj(1−k=1∑Mbi(k))
FOC 为(注意,只有 o t = v k o_t=v_k ot=vk 时 b j ( o t ) b_j(o_t) bj(ot) 对 b j ( k ) b_j(k) bj(k) 的偏导数才不为 0,这里用指示函数来表示):
∂ L ( b ) ∂ b j ( k ) = ∑ t = 1 T P ( O , i t = q j ∣ λ ^ ) I ( o t = v k ) b j ( k ) + γ j = 0 ⇒ ∑ t = 1 T P ( O , i t = q j ∣ λ ^ ) I ( o t = v k ) + b j ( k ) γ j = 0 \begin{aligned} \frac{\partial L(b)}{\partial b_{j}(k)} =&\, \frac{\sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda)I(o_t=v_k)}{b_{j}(k)}+\gamma_j=0 \\ \Rightarrow &\, \sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda)I(o_t=v_k)+b_{j}(k)\gamma_j=0 \end{aligned} ∂bj(k)∂L(b)=⇒bj(k)t=1∑TP(O,it=qj∣λ^)I(ot=vk)+γj=0t=1∑TP(O,it=qj∣λ^)I(ot=vk)+bj(k)γj=0
将所有 j j j 相同的 FOC 相加,得到(因为有且仅有一个 k k k 使得 I ( o t = v k ) = 1 I(o_t=v_k)=1 I(ot=vk)=1):
γ j = − ∑ t = 1 T P ( O , i t = q j ∣ λ ^ ) \gamma_j=-\sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda) γj=−t=1∑TP(O,it=qj∣λ^)
代回解得:
b j ( k ) = ∑ t = 1 T P ( O , i t = q j ∣ λ ^ ) I ( o t = v k ) ∑ t = 1 T P ( O , i t = q j ∣ λ ^ ) b_j(k)=\frac{\sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda)I(o_t=v_k)}{\sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda)} bj(k)=t=1∑TP(O,it=qj∣λ^)t=1∑TP(O,it=qj∣λ^)I(ot=vk)
参数估计公式
以上参数估计的公式可以使用前向概率和后向概率表示,即:
a i j = ∑ t = 1 T − 1 ξ t ( i , j ) ∑ t = 1 T − 1 γ t ( i ) , b j ( k ) = ∑ t = 1 , o t = v k T γ t ( i ) ∑ t = 1 T γ t ( i ) , π i = γ 1 ( i ) a_{ij}=\frac{\sum\limits_{t=1}^{T-1}\xi_{t}(i,j)}{\sum\limits_{t=1}^{T-1}\gamma_t(i)} ,\quad\quad b_j(k)=\frac{\sum\limits_{t=1,o_t=v_k}^{T}\gamma_t(i)}{\sum\limits_{t=1}^{T}\gamma_t(i)} ,\quad\quad \pi_i=\gamma_1(i) aij=t=1∑T−1γt(i)t=1∑T−1ξt(i,j),bj(k)=t=1∑Tγt(i)t=1,ot=vk∑Tγt(i),πi=γ1(i)
算法描述
输入:观测数据 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,\,o_2,\,\cdots,\,o_T) O=(o1,o2,⋯,oT) ;
输出:HMM 参数
- 初始化,对 n = 0 n=0 n=0 ,选取模型参数初始值 a i j ( 0 ) a_{ij}^{(0)} aij(0) , b j ( k ) ( 0 ) b_{j}(k)^{(0)} bj(k)(0) , π i ( 0 ) \pi_i^{(0)} πi(0) ;
- 递推,对于 n = 1 , 2 , ⋯ n=1,\,2,\,\cdots n=1,2,⋯ ,使用前一次递推得到的参数计算前向概率和后向概率,并更新参数:
a i j = ∑ t = 1 T − 1 ξ t ( i , j ) ∑ t = 1 T − 1 γ t ( i ) , b j ( k ) = ∑ t = 1 , o t = v k T γ t ( i ) ∑ t = 1 T γ t ( i ) , π i = γ 1 ( i ) a_{ij}=\frac{\sum\limits_{t=1}^{T-1}\xi_{t}(i,j)}{\sum\limits_{t=1}^{T-1}\gamma_t(i)} ,\quad\quad b_j(k)=\frac{\sum\limits_{t=1,o_t=v_k}^{T}\gamma_t(i)}{\sum\limits_{t=1}^{T}\gamma_t(i)} ,\quad\quad \pi_i=\gamma_1(i) aij=t=1∑T−1γt(i)t=1∑T−1ξt(i,j),bj(k)=t=1∑Tγt(i)t=1,ot=vk∑Tγt(i),πi=γ1(i)
- 中止,得到模型参数 λ ( n + 1 ) = ( A ( n + 1 ) , B ( n + 1 ) , π ( n + 1 ) ) \lambda^{(n+1)}=(A^{(n+1)},\,B^{(n+1)},\,\pi^{(n+1)}) λ(n+1)=(A(n+1),B(n+1),π(n+1)) ;
解码问题
解码问题是指,已知模型参数,给定观测序列,求出最有可能的对应的状态序列。
近似算法
回忆一下前面 γ t ( i ) \gamma_{t}(i) γt(i) 的定义是:给定模型 λ \lambda λ 和观测序列 O O O ,在时刻 t t t 处于状态 q i q_i qi 的概率。
近似算法是直接使用每一个时刻出现概率最大的状态作为输出,即:
i t ∗ = arg max 1 ≤ i ≤ N [ γ t ( i ) ] , t = 1 , 2 , ⋯ , T i_t^\ast=\arg \max_{1\leq i\leq N}[\gamma_t(i)],\quad t=1,2,\cdots,T it∗=arg1≤i≤Nmax[γt(i)],t=1,2,⋯,T
从而得到状态序列 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) I^\ast=(i_1^\ast,i_2^\ast,\cdots,i_T^\ast) I∗=(i1∗,i2∗,⋯,iT∗) 。
近似算法顾名思义,就是近似的,没有更多地考虑到状态转移概率 a i j a_{ij} aij ,但是它计算简单。
Viterbi 算法
维特比算法实际上是动态规划,属于精确算法。原理为:最优路径的子路径一定是最优的(这里的最优指的是概率最大)。例如,若最优路径在 t t t 时刻经过节点 i t ∗ i_t^\ast it∗ ,则从 i t ∗ i_t^\ast it∗ 到 i T ∗ i_T^\ast iT∗ 的子路径一定是所有从 i t ∗ i_t^\ast it∗ 到 i T ∗ i_T^\ast iT∗ 的路径中最优的。否则我们可以选择更优的从 i t ∗ i_t^\ast it∗ 到 i T ∗ i_T^\ast iT∗ 的路径去替换原来的子路径,得到更优的总的路径。因此,我们从 t = 1 t=1 t=1 开始,递推地计算时刻 t t t 状态为 i i i 的各部分路径的最大概率,直至时刻 t = T t=T t=T 。
我们定义变量 δ \delta δ ,代表时刻 t t t 状态为 i i i 的所有单个路径 ( i 1 , i 2 , ⋯ , i t ) (i_1,i_2,\cdots,i_t) (i1,i2,⋯,it) 中概率的最大值:
δ t ( i ) = max ( i 1 , i 2 , ⋯ , i t ) P ( i t = i , o t , ⋯ , o 1 ∣ λ ) , i = 1 , 2 , ⋯ , N \delta_t(i)=\max_{(i_1,i_2,\cdots,i_t)} P(i_t=i,o_t,\,\cdots,o_1|\lambda),\quad i=1,2,\cdots,N δt(i)=(i1,i2,⋯,it)maxP(it=i,ot,⋯,o1∣λ),i=1,2,⋯,N
假设一个共同的起始节点为 q 0 q_0 q0 ,其到每个状态的转移概率为每个状态对应的初始概率,即 a 0 i = π i a_{0i}=\pi_i a0i=πi 。
假设我们前面已经计算了时刻 [ 0 , t ] [0,\,t] [0,t] ,得到了 0 0 0 时刻从 i 0 = q 0 i_0=q_0 i0=q0 节点出发, t t t 时刻到达各个节点的最优路径和对应的概率 δ t ( j ) \delta_{t}(j) δt(j) 。则计算 t + 1 t+1 t+1 时刻时,对于某个状态 q i q_i qi ,我们只需求得 j = arg max j δ t ( j ) a j i b j ( o t + 1 ) j=\arg\max\limits_j \delta_{t}(j)a_{ji}b_{j}(o_{t+1}) j=argjmaxδt(j)ajibj(ot+1) ,则说明 δ t + 1 ( i ) = δ t ( j ) a j i b j ( o t + 1 ) \delta_{t+1}(i)=\delta_{t}(j)a_{ji}b_{j}(o_{t+1}) δt+1(i)=δt(j)ajibj(ot+1) ,并且 0 0 0 时刻从 i 0 i_0 i0 节点出发, t + 1 t+1 t+1 时刻到达状态 q i q_i qi 的最优路径中,前一个节点的状态就是 q j q_j qj 。
相应的递推公式为:
δ t + 1 ( i ) = max 1 ≤ j ≤ N δ t ( j ) a j i b j ( o t + 1 ) , i = 1 , 2 , ⋯ , N ; t = 1 , 2 , ⋯ , T − 1 \delta_{t+1}(i)=\max_{1\leq j\leq N}\delta_{t}(j)a_{ji}b_{j}(o_{t+1}), \quad i=1,2,\cdots,N;\quad t=1,2,\cdots,T-1 δt+1(i)=1≤j≤Nmaxδt(j)ajibj(ot+1),i=1,2,⋯,N;t=1,2,⋯,T−1
算法中需要记录这个 q j q_j qj ,我们定义变量 Ψ t ( i ) \Psi_t(i) Ψt(i) ,代表时刻 t t t 状态为 q i q_i qi 的所有单个路径 ( i 1 , i 2 , ⋯ , i t − 1 , i t ) (i_1,i_2,\cdots,i_{t-1},i_t) (i1,i2,⋯,it−1,it) 中概率最大的路径的第 t − 1 t-1 t−1 个节点为:
Ψ t ( i ) = arg max 1 ≤ j ≤ N δ t ( j ) a j i b j ( o t + 1 ) , i = 1 , 2 , ⋯ , N \Psi_{t}(i)=\arg\max_{1\leq j\leq N}\delta_{t}(j)a_{ji}b_{j}(o_{t+1}),\quad i=1,2,\cdots,N Ψt(i)=arg1≤j≤Nmaxδt(j)ajibj(ot+1),i=1,2,⋯,N
(我觉得算法中计算的东西可以叫做最优前缀子路径)
最后,当计算完所有最优前缀子路径后,我们取 i = arg max i δ t ( i ) i=\arg\max\limits_i \delta_t(i) i=argimaxδt(i) ,则说明我们所要求的总的最优路径的最后一个节点的状态是 q i q_i qi ,此时只需按照所记录的前一个节点的状态递推回去,就能得到整个最优路径。
算法:维比特算法
- 输入:模型 λ = ( A , B , π ) \lambda=(A,\,B,\,\pi) λ=(A,B,π) 和观测 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,\,o_2,\,\cdots,o_T) O=(o1,o2,⋯,oT) ;
- 输出:最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) I^\ast=(i_1^\ast,i_2^\ast,\cdots,i_T^\ast) I∗=(i1∗,i2∗,⋯,iT∗) ;
- 初始化:
δ 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , ⋯ , N Ψ 1 ( i ) = 0 , i = 1 , 2 , ⋯ , N \begin{array}{c} \delta_1(i)=\pi_i b_i(o_1),\quad i=1,2,\cdots ,N \\ \Psi_1(i)=0, \quad i=1,2,\cdots,N \end{array} δ1(i)=πibi(o1),i=1,2,⋯,NΨ1(i)=0,i=1,2,⋯,N
- 递推,对于 t = 2 , 3 , ⋯ , T t=2,3,\cdots,T t=2,3,⋯,T :
δ t ( i ) = max 1 ≤ j ≤ N δ t − 1 ( j ) a j i b i ( o t ) , i = 1 , 2 , ⋯ , N Ψ t ( i ) = arg max 1 ≤ j ≤ N δ t − 1 ( j ) a j i b i ( o t ) , i = 1 , 2 , ⋯ , N \begin{array}{c} \delta_{t}(i)=\max\limits_{1\leq j\leq N}\delta_{t-1}(j)a_{ji}b_{i}(o_{t}), \quad i=1,2,\cdots,N \\ \Psi_{t}(i)=\arg\max_{1\leq j\leq N}\delta_{t-1}(j)a_{ji}b_{i}(o_{t}),\quad i=1,2,\cdots,N \end{array} δt(i)=1≤j≤Nmaxδt−1(j)ajibi(ot),i=1,2,⋯,NΨt(i)=argmax1≤j≤Nδt−1(j)ajibi(ot),i=1,2,⋯,N
注意,这里 Ψ t ( i ) \Psi_t(i) Ψt(i) 的表达式也可以写成以下形式,因为 b i ( o t ) b_i(o_t) bi(ot) 对于第 t − 1 t-1 t−1 层而言是个常数,乘不乘进去都可以,反正对大家来说都是一样的效果:
Ψ t ( i ) = arg max 1 ≤ j ≤ N δ t − 1 ( j ) a j i , i = 1 , 2 , ⋯ , N \Psi_{t}(i)=\arg\max_{1\leq j\leq N}\delta_{t-1}(j)a_{ji},\quad i=1,2,\cdots,N Ψt(i)=arg1≤j≤Nmaxδt−1(j)aji,i=1,2,⋯,N
- 中止:
P ∗ = max 1 ≤ i ≤ N δ T ( i ) i T ∗ = arg max 1 ≤ i ≤ N δ T ( i ) \begin{array}{c} P^\ast=\max\limits_{1\leq i\leq N}\delta_T(i) \\ i^\ast_T=\arg \max\limits_{1\leq i\leq N}\delta_T(i) \end{array} P∗=1≤i≤NmaxδT(i)iT∗=arg1≤i≤NmaxδT(i)
- 最优路径回溯:对于 t = T − 1 , T − 2 , ⋯ , 1 t=T-1,T-2,\cdots,1 t=T−1,T−2,⋯,1 :
i t ∗ = Ψ t + 1 ( i t + 1 ∗ ) i^\ast_t=\Psi_{t+1}(i_{t+1}^\ast) it∗=Ψt+1(it+1∗)
即得到最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) I^\ast=(i_1^\ast,i_2^\ast,\cdots,i_T^\ast) I∗=(i1∗,i2∗,⋯,iT∗) ;
例(盒子和球模型):状态集合为 Q = { 1 , 2 , 3 } Q=\set{1,\,2,\,3} Q={1,2,3},观测集合为 V = { r , w } V=\set{r,\,w} V={r,w} ,
A = [ 0.5 0.2 0.3 0.3 0.5 0.2 0.2 0.3 0.5 ] B = [ 0.5 0.5 0.4 0.6 0.7 0.3 ] π = [ 0.2 0.4 0.4 ] A=\begin{bmatrix} 0.5 & 0.2 & 0.3\\ 0.3 & 0.5 & 0.2\\ 0.2 & 0.3 & 0.5\\ \end{bmatrix} \quad B=\begin{bmatrix} 0.5 & 0.5 \\ 0.4 & 0.6\\ 0.7 & 0.3\\ \end{bmatrix} \quad \pi=\begin{bmatrix} 0.2\\ 0.4\\ 0.4\\ \end{bmatrix} A= 0.50.30.20.20.50.30.30.20.5 B= 0.50.40.70.50.60.3 π= 0.20.40.4
假设得到的观测序列为 O = ( r , w , r ) O=(r,\,w,\,r) O=(r,w,r) ,则计算过程为:
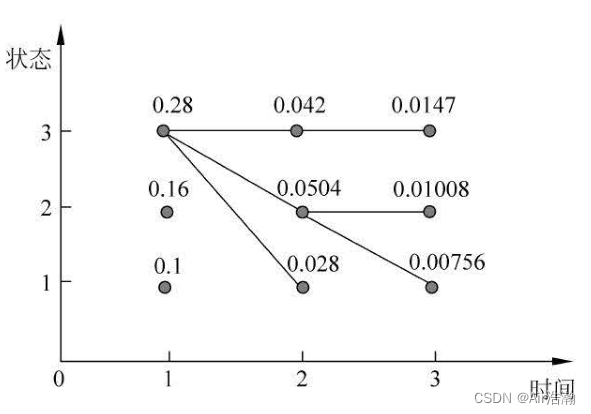
最优路径为 I ∗ = ( 3 , 3 , 3 ) I^\ast=(3,\,3,\,3) I∗=(3,3,3) ;
相关文章:

统计学习方法 隐马尔可夫模型
文章目录 统计学习方法 隐马尔可夫模型基本概念概率计算问题直接计算法前向算法后向算法前向概率和后向概率 学习问题监督学习算法Baum-Welch 算法E 步M 步参数估计公式算法描述 解码问题近似算法Viterbi 算法 统计学习方法 隐马尔可夫模型 读李航的《统计学习方法》时&#x…...

Cypress 与 Selenium WebDriver
功能测试自动化工具的王座出现了新的争夺:Cypress.io。赛普拉斯速度快吗?是的。赛普拉斯是交互式的吗?是的。赛普拉斯可靠吗?你打赌。最重要的是……这很酷! 但 Cypress 是Selenium WebDriver的替代品吗?S…...

Leetcode 第 365 场周赛题解
Leetcode 第 365 场周赛题解 Leetcode 第 365 场周赛题解题目1:2873. 有序三元组中的最大值 I思路代码复杂度分析 题目2:2874. 有序三元组中的最大值 II思路代码复杂度分析思路2 题目3:2875. 无限数组的最短子数组思路代码复杂度分析 题目4&a…...

什么是软件测试? 软件测试都有什么岗位 ?软件测试和调试的区别? 软件测试和开发的区别?软件测试等相关概念入门篇
1、什么是软件测试? 常见理解: 软件测试就是找BUG,发现缺陷 真正理解: 软件测试就是验证软件产品特性是否满足用户的需求 测试定义: 测试人员验证软件是否符合需求的这个过程就是测试 2、为什么要有测试 标准情况下&a…...

VI/VIM的使用
1、vi的基本概念 基本上vi可以分为三种状态,分别是命令模式(command mode)、插入模式(Insert mode)和底行模式(last line mode),各模式的功能区分如下: 1) 命令行模…...

【虹科干货】Redis Enterprise vs ElastiCache——如何选择缓存解决方案?
使用Redis 或 Amazon ElastiCache 来作为缓存加速已经是业界主流的解决方案,二者各有什么优势?又有哪些区别呢? 文况速览: - Redis 是什么? - Redis Enterprise 是什么? - Amazon ElastiCache 是什么&…...
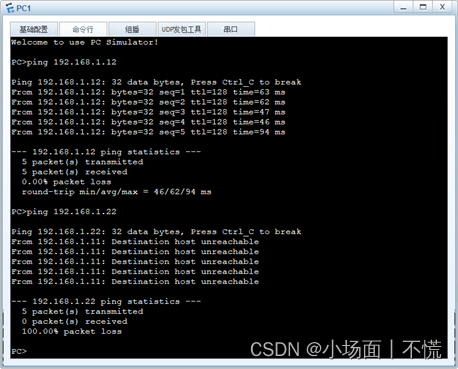
2.2.2 交换机间相同vlan的通信
实验2.2.2 交换机间相同vlan的通信 一、任务描述二、任务分析三、实验拓扑四、具体要求五、任务实施1.设置交换机的名称,创建VLAN,配置access并分配接口。对两台交换机进行相同的VLAN划分,下面是SWA配置过程,同理可实现SWB的配置。…...

C的魅力在于指针
原有的adrv9025 代理框架很好用,在其原有的平台上做改进...

【Linux常用命令14】Linux系统监控常用命令
proc文件系统 /proc/cmdline 加载kernel时的相关指令与参数 /proc/cpuinfo CPU相关信息,包含频率、类型与运算功能 /proc/devices 记录了系统各个主要设备的主设备号码 /proc/filesystems 记录系统加载的文件系统 /proc/loadavg 平均负载值 top看到就是这个 /proc/…...

Python Watchdog:高效的文件系统监控
1. 写在前面 在软件开发中,有时候需要通过 Python 去监听指定区域文件或目录的创建、修改,或者删除,从而引发特定的事件处理。本篇博客为你介绍第三方模块 Watchdog 实现对文件事件的监控。 公众号: 滑翔的纸飞机 2. Watchdog 2…...

C++中多态的原理【精华】
虚函数表 通过一道题我们先感受一下编译器针对多态的处理 #include <iostream> using namespace std;class Base { public:virtual void Func1(){cout << "Func1()" << endl;} private:int _b 1;char _c };int main() {cout << sizeof(B…...

亿赛通电子文档安全管理系统 Update.jsp SQL注入
目录 0x01 漏洞介绍 0x02 影响产品 0x03 语法特征 0x04 漏洞复现页面 0x05 漏洞修复建议 0x01 漏洞介绍 亿赛通电子文档安全管理系统是国内最早基于文件过滤驱动技术的文档加解密产品之一,保护范围涵盖终端电脑(Windows、Mac、Linux系统平台&#…...

神经网络中的反向传播:综合指南
塔曼纳 一、说明 反向传播是人工神经网络 (ANN) 中用于训练深度学习模型的流行算法。它是一种监督学习技术,用于调整网络中神经元的权重,以最小化预测输出和实际输出之间的误差。 在神经网络中,反向传播是计算损失函数…...

协同创新、奔赴未来——“华为云杯”2023人工智能创新应用大赛华丽谢幕
9月27日,在苏州工业园区管理委员会、华为云计算技术有限公司的指导下,由SISPARK(苏州国际科技园)、华为(苏州)人工智能创新中心联合主办,东北大学工业智能与系统优化国家级前沿科学中心、浙江大…...

介绍Node.js中fs模块 代码和注释。
Node.js中的fs模块提供了一些用于文件系统操作的API,包括文件读写、目录操作等。 读取文件 使用fs.readFile()方法可以读取文件内容。该方法的第一个参数是文件路径,第二个参数是可选的选项对象,第三个参数是回调函数。回调函数的第一个参数…...

【QT 读取JSON】 深入浅出 使用QT内置的QJson模块解析Json文件 匠心之作
目录 0 引言1 Json数据分析2 解析Json数据 🙋♂️ 作者:海码007📜 专栏:QT专栏💥 标题:【QT 读取JSON】 使用QT内置的QJson模块解析Json文件❣️ 寄语:人生的意义或许可以发挥自己全部的潜力&…...

初识javaweb2 tomcat
如果是tomcat启动成功却无法通过localhost:8080进入页面,先去查看是否是端口号被占用, 再用命令中断占用的进程,如果简单的命令窗口无法中断,切换到管理员身份运行即可 netstat -ano|findstr "8080" 查看那个进程占用了…...

使用OPENROWSET :在一个数据库中查询另一个数据库的数据
当你需要在一个数据库中查询另一个数据库的数据时,SQL Server提供了多种方法来实现这一目标。一种常见的方法是使用链接服务器(Linked Server),另一种方法是使用 OPENROWSET 函数。本篇博客将重点介绍如何使用 OPENROWSET 函数在当…...
)
基于STM32设计的智慧农业管理系统(ESP8266+腾讯云微信小程序)
一、项目介绍 基于STM32设计的智慧农业控制系统(ESP8266+腾讯云微信小程序) 1.1 项目背景 随着人们对食品安全和生态环境的日益重视,智慧农业逐渐成为一个备受关注的领域。智能化管理可以提高农业生产效率,减少资源浪费,改善生态环境。因此,基于物联网技术的智慧农业管理系…...
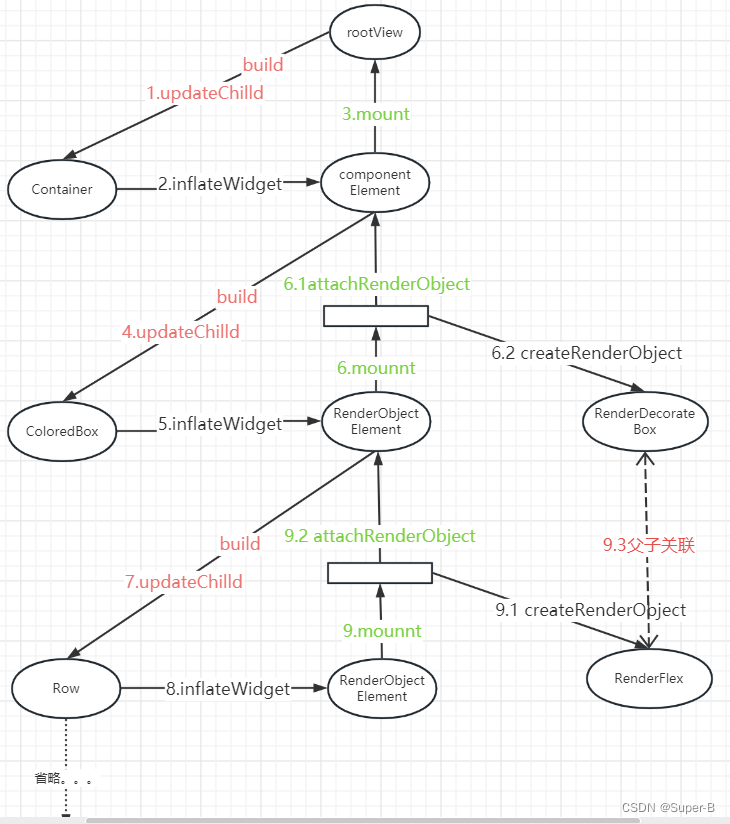
Flutter视图原理之三棵树的建立过程
目录 三棵树的关系树的构建过程1.updateChild函数(element的复用)2.inflateWidget函数3.mount函数3.1 componentElement的实现3.2 RenderObjectElement的实现3.2.1 attachRenderObject函数 4.performRebuild函数 总结三棵树创建流程 三棵树的关系 Flutt…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
