从头开始机器学习:逻辑回归
一、说明
二、逻辑回归简介
我们将以我们在线性回归中探索的想法为基础,所以如果你还没有读过那个博客,我建议你这样做。尽管 Logistic 回归的名称,但不涉及回归,它实际上是一个分类模型。分类算法用于将数据分类到特定类中。例如,将一组手写数字分类为从 0 到 9 的关联数字,或者对图像是狗还是猫进行分类。
2.1 线性分级机
遵循线性回归的相同理念,将机器学习视为几何问题,现在我们不再绘制最适合数据的线,而是绘制一条最能将数据分隔到各自类中的线。考虑下面的数据,假设紫色点代表类 1,黄点代表类 0。
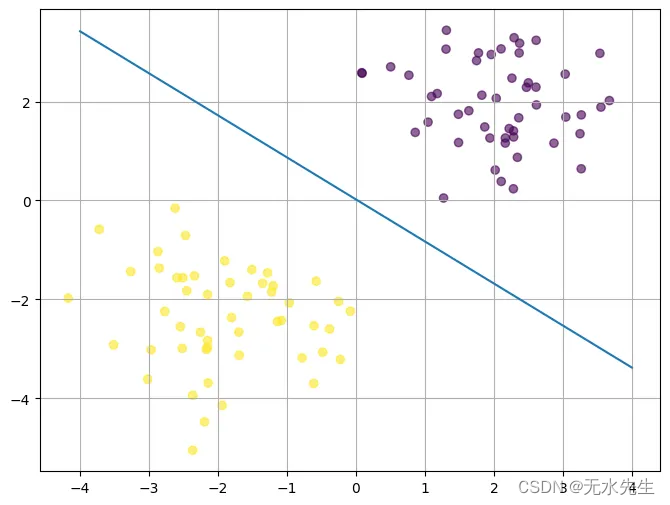
例如,这 2 个类别可能是两种不同的花种,x 轴可以是花瓣宽度,y 轴可以是花瓣长度。每个物种都有自己独特的叶子大小,与其他花不同。请记住,所有数据都是相同的,应用程序在任何环境中都是相同的。我们可以将模型解释为直线方程,但现在我们将 x 和 y 作为输入
![]()
假设我们选择线上方的紫色点
![]()
现在让我们选择线下方的黄色点
![]()
请注意,如果我们选择线上方的点,输出为负,如果我们选择线下方的点,则输出为正,这就是我们对任何新数据点进行分类的方式。如果点直接位于线上,则结果将为 0,即无类。通常,对于 D 输入,方程可以写成。
![]()
线性分类器模型
您会注意到这与线性回归相同,这就是为什么线性回归是先决条件的原因,它将使理解逻辑回归变得更加容易,因为您已经拥有使用向量、矩阵微积分和机器学习中使用的整体符号的经验。这仅仅是个开始,这个模型被称为线性分类器,我们将继续在这个模型的基础上构建 Logistic 回归模型。
2.2 神经元
在机器学习的早期,人们对尝试对人脑进行建模并创建类似于人脑的机器学习模型非常感兴趣。“感知器”算法背后的想法受到人脑神经元的启发。逻辑回归与感知器算法非常相似。
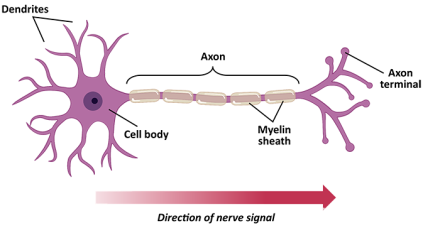
如果我们看一下人脑中的神经元,你会发现它从树突中吸收多个输入,如果动作电位足够强,它会通过轴突末端产生输出。
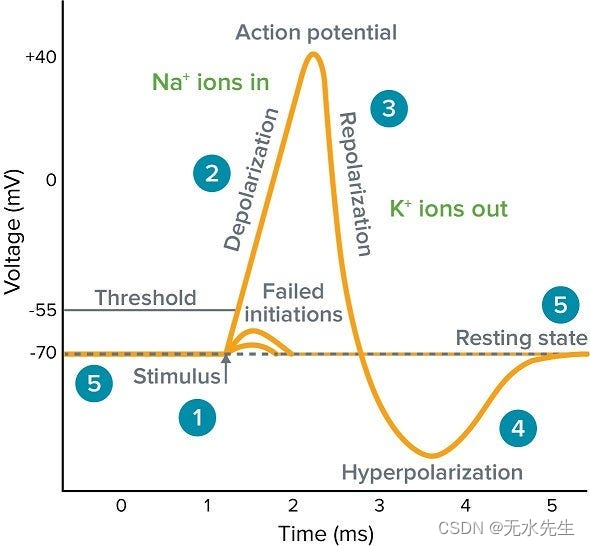
这会产生“全有或全无”行为,其中神经元仅在电压超过阈值时才触发。因此,生物神经元的输出可以是1或0,开或关。我们的逻辑回归模型从人脑神经元的结构和机制中汲取灵感,您很快就会看到。
2.3 设置模型
如果您之前对模型进行试验,您会注意到线下方的点更“正”,线上方的点更“负”,靠近线的点接近 0。当该点看起来离直线更远时,我们可以推断出它属于该类的概率增加,而属于其他类的概率减小。当点越来越接近线时,它变得更加不确定,并且属于任一类的概率变为 50/50。我们希望扩展当前的线性分类器模型,因此它输出该点属于某个类的概率。我们可以从线性分类器获取输出,并通过“激活函数”将其归一化为介于 0 和 1 之间。您可以选择多个激活函数,但现在,让我们坚持使用 sigmoid。

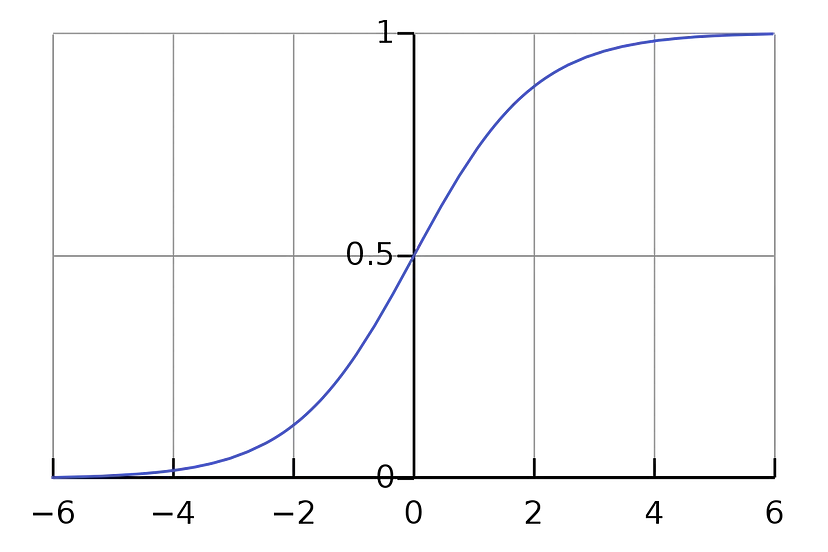
现在我们可以将模型解释为属于类别 y 的条件概率。现在不要混淆,我们使用y作为我们的“目标”,x是D输入的单个样本。
![]()
由于 x 属于 y=1 和 y=0 的概率必须加起来为 1,我们也得到
![]()
这很好,因为我们可以简单地对概率进行四舍五入以获得预测值。因此,如果属于类 1 的概率是 0.7,我们可以将其四舍五入为 1。如果属于类 1 的概率为 0.2,我们可以向下舍入得到 0 的预测。
现在我们的模型的快速可视化
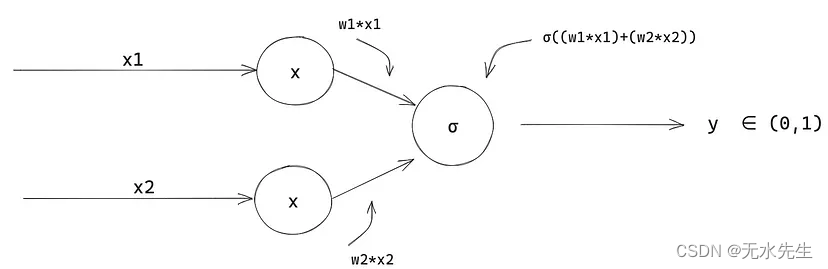
有趣的是,我们的模型看起来与生物神经元相似,您可能还想知道这是否与神经网络有关?我们正在构建的模型通常被称为神经网络的“神经元”,神经网络本质上是许多逻辑回归函数的网络。
2.4 变量回顾
当我第一次学习神经网络和逻辑回归时,最困难的事情实际上是记住所有变量的含义和大小。因此,在继续之前,让我们快速回顾一下。线性回归博客中的变量几乎相同。
- N = 样品
数 - 测量 10 个个体的重量,N=10 - D = 每个样本
的特征数 - 测量身高、体重和年龄以预测血压。D=3 - w = 大小为 Dx1 的权重矢量
- X = 大小为 NxD
的数据矩阵 - 每行都是一个样本,而每一列都是该样本的一个特征 - x = 大小为 Dx1 的单个样本
通常,大写字母表示矩阵,而小写字母表示向量。
- yn = 来自第 n 个样本的模型的单个目标标签或预测
- Y = 模型中的所有目标标签或预测作为大小为 Nx1 的向量
- tn = 第 n 个样本中的单个目标标签
- T = 所有目标标签作为大小为 Nx1 的向量
- P(y=1|x) = 我们模型的概率预测
现在,我们对 Y 有两种不同含义的原因是让我们的推导更容易编写。写P(y=1|x) 在做推导时,所以我们设置 P(y=1|x) = y 并改用 t 作为我们的目标。如果同时看到 t 和 y,假设 t=目标和 y=预测
- 误差函数 = 成本函数 = 目标函数
一般来说,我们总是会最小化我们的误差/成本函数,这是不言自明的。目标函数可能会根据上下文最小化或最大化。这只是一个微不足道的符号翻转场景,其中最小化 x² = 最大化 -x²。一旦我们探索了交叉熵和对数似然,这一点就会变得明显。
2.5 设置错误函数
现在,让我们设置一种方法来测量模型中的误差。最初的想法可能是只使用线性回归中的均方误差函数(MSE)。如果我们分解我们的问题,我们将意识到MSE函数在这种情况下并不理想。首先,MSE假设误差呈高斯分布,但是逻辑回归模型中的每个预测都遵循伯努利分布。其次,如果我们的模型对完全错误的答案非常有信心,我们希望我们的误差呈指数级增长。这不能使用MSE的二次性质进行建模。我们问题的本质是植根于概率的问题,因此选择一个源于概率的错误函数是有意义的。我们可以从信息论中借用“熵”的概念。如果你不了解信息熵,我建议你观看这个介绍这个主题的视频。
2.6 交叉熵误差
我们可以使用负对数函数来模拟我们的错误
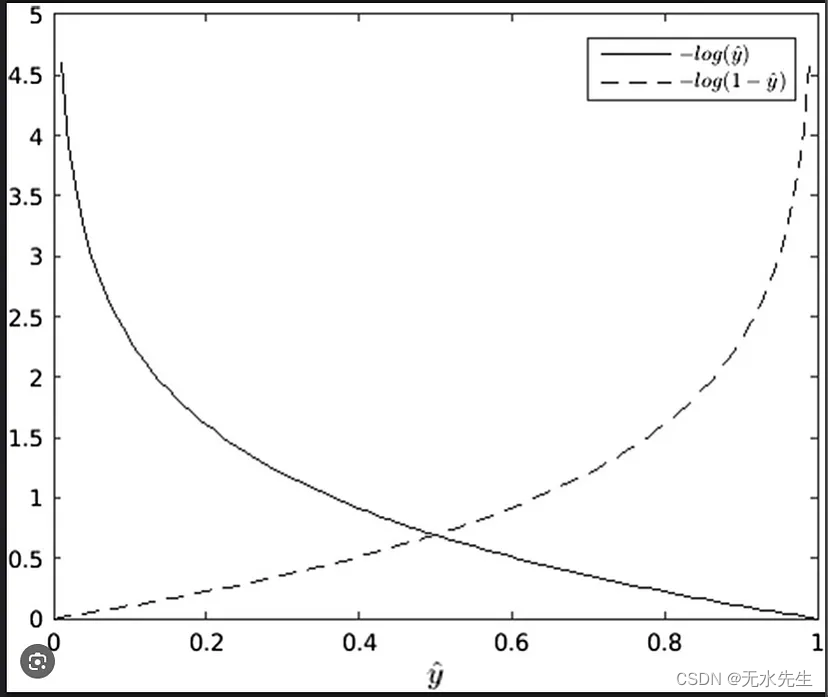
实线表示目标=1,虚线表示目标=0
当我们的预测为 1 且目标为 1 时,我们的误差为零,但误差呈指数增长,我们的模型对错误答案的置信度越高,反之亦然,如果我们的预测为 0。这被称为交叉熵误差,公式就是。
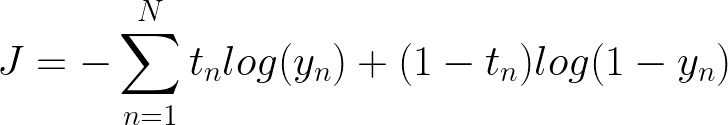
请注意,如果我们的目标是 1,其中一个日志将乘以零,反之亦然。
我们的目标是最小化这种交叉熵误差。如果现在看起来令人困惑,我们还将研究另一种使用最大似然推导此公式的方法,这将进一步巩固您的理解。
2.7 最大似然
最大似然会产生与交叉熵误差几乎相同的误差公式,但在我看来,如果您不了解熵的工作原理,与交叉熵误差函数相比,它更直观一些。此外,在进行梯度下降时,这将使推导更容易一些。
假设我们正在抛硬币,但我们不知道它是否公平。我们不知道翻转正面或反面的概率。我们掷硬币 10 次,观察到 8 个正面和 2 个反面。观察到此结果的可能性为
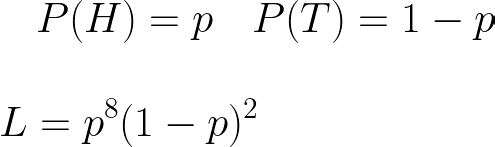
我们想弄清楚硬币的概率,使观察这些数据的可能性最大化。我们希望相对于 L 最大化 p。在这种情况下,我们将通过获取双方的对数来最大化对数可能性。为什么?最终结果仍然相同,因为对数是一个单调递增的函数(如果 a>b 则 log(a) > log(b) 也为真)。使用乘积规则对数,它将使我们的推导变得更加容易。请注意,在机器学习中,log 表示自然日志。
为了最大化对数似然,我们可以取导数并求解 p。
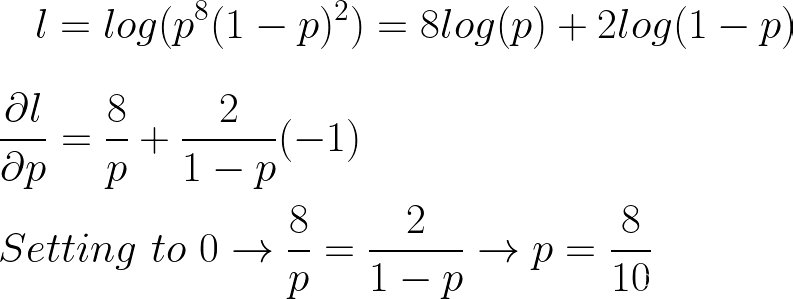
这个新的“l”=对数似然
在我们的问题中,我们对大小为 N 的数据的观察。此数据的标签是 0 和 1 的序列,而不是正面和反面。我们想计算出给定x(输入)的模型的概率,该概率使观察这些数据的可能性最大化。让我们回顾一下模型的定义。
![]()
我们的概率取决于 x!
设置问题
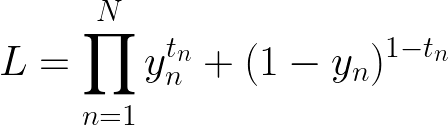
tn 是目标,因此 0 或 1
我们有一个概率乘积,迭代我们的 N 个样本。现在你会注意到为什么在这里获取日志非常有用。
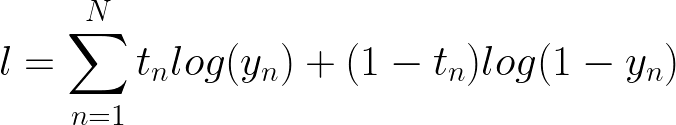
目标函数
使用对数的乘积规则,我们可以将其转换为求和而不是乘积。现在这与我们的交叉熵误差相同,只是它缺少负号。这是因为我们正在最大化对数似然,而不是最小化,就像在交叉熵误差中一样。
2.8 练习:求解重量
让我们从取交叉熵函数的导数开始,因为我们正在求解我们想要将导数 wrt 取到每个权重 w 的权重。我们的权重嵌套在一堆其他函数中,当我们遇到这种情况时,使用链式规则是有意义的。我们可以使用链式规则将导数拆分为 3 个导数。首先是取我们的交叉熵函数的导数,然后取 sigmoid 函数的导数,最后取 w 本身的导数。
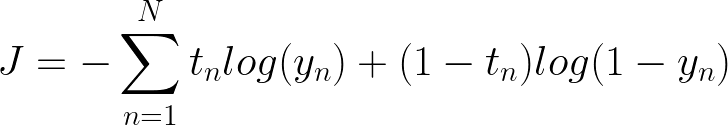
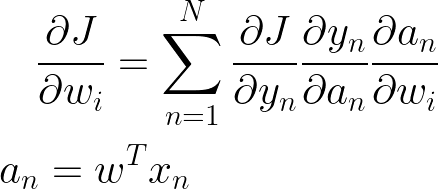
尝试自己派生解决方案,也尝试矢量化解决方案,以便我们可以轻松地在 NumPy 中编写所有内容。这意味着重新安排解决方案以利用NumPy的点积功能。
2.9 解决
让我们取关于 yn 的一阶导数
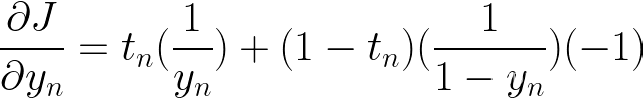
接下来取 yn 关于 (激活函数) 的导数

最后取一个 with resepct 的导数到 wi,我们在做线性回归时已经计算过了
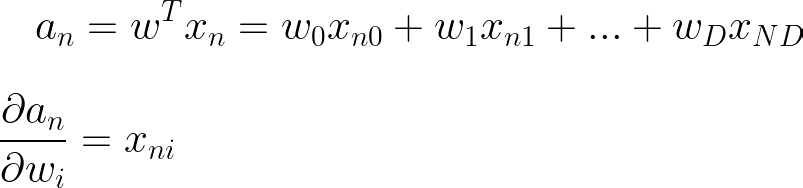
现在我们可以组合结果来计算最终导数
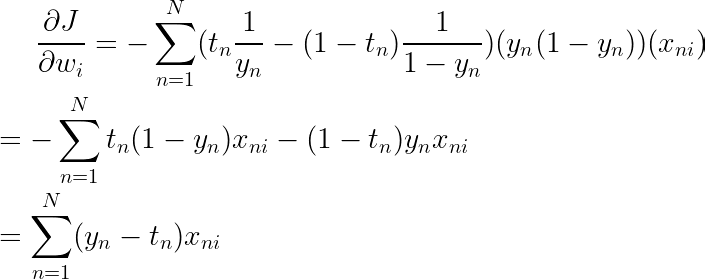
我们可以矢量化这个等式
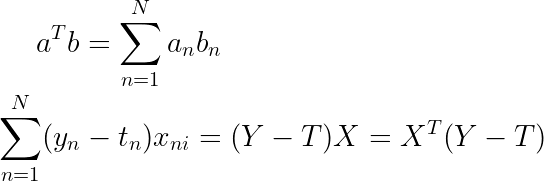
让我们快速仔细检查矩阵乘法的大小,以便我们知道我们没有做错任何事,并且我们的输出是正确的大小。我们的输出应该是大小为 Dx1 的矢量,用于我们所有权重的梯度。
![]()
现在,您可以尝试通过将导数设置为 0 来求解权重,但不幸的是,此导数没有闭式解。
2.10 梯度下降/上升
我们可以使用一种迭代方法,在误差函数的局部最小值方向上采取小步骤来找到最佳权重,这称为梯度下降。
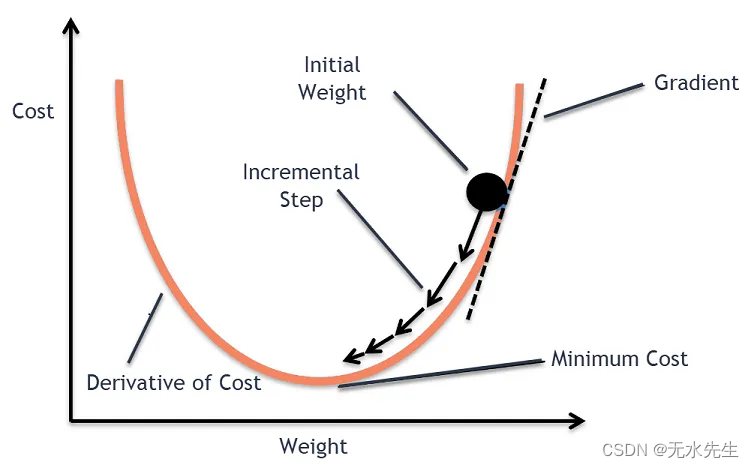
请注意,这并不能保证找到全局最小值,只能保证找到局部最小值
步长也称为学习率,是我们朝着最低成本方向采取的步骤的大小。我们设置什么学习率?嗯,它主要是直觉,我们希望设置一个足够大的学习率,这样学习过程就不会进行太多迭代,但也足够小,这样我们就不会超过最小值,然后围绕它振荡。在实践中,您希望在梯度下降时观察误差。让我们做一个简单的例子来巩固这个想法

我们知道 J 的最小值是 x=0,但假装我们不知道
- 迭代 1:w = 5 -0.1*10 = 4
- 迭代 2:w=4 – 0.1*8= 3.2
- 迭代 3:w=3.2 -0.1*6.4 = 2.65
现在,如果您还没有做过微积分 3,您应该对梯度下降的工作原理有一个很好的了解。如果我们试图最大化一个值,只需将公式中的符号从负数切换到正数即可。这样,您可以选择最小化交叉熵误差或最大化对数似然,这两种方法都会产生相同的结果。
2.11 练习:对模型进行编码
在 repo 中有一个名为“logisitic_regression_practice”的文件,在您的编辑器中打开它,并使用您学到的填写变量和函数。另外,请确保下载数据“logistic_data.csv”。如果您想要额外的挑战,请尝试在没有帮助的情况下从头开始编写模型。只需加载logisitic_data即可。如果您遇到困难,您可以随时查看名为“logisitic_regression_solution”的解决方案。
三、多类逻辑回归
假设现在我们要对 2 个以上的东西进行分类,到目前为止我们一直在进行二元分类,我们的目标是“0”或“1”。如果我们想使用多个类,我们的原始模型将不起作用。让我们继续使用一些几何图形来帮助我们构建直觉。假设我们现在预测的不是预测 2 个类,而是预测 3 个类。
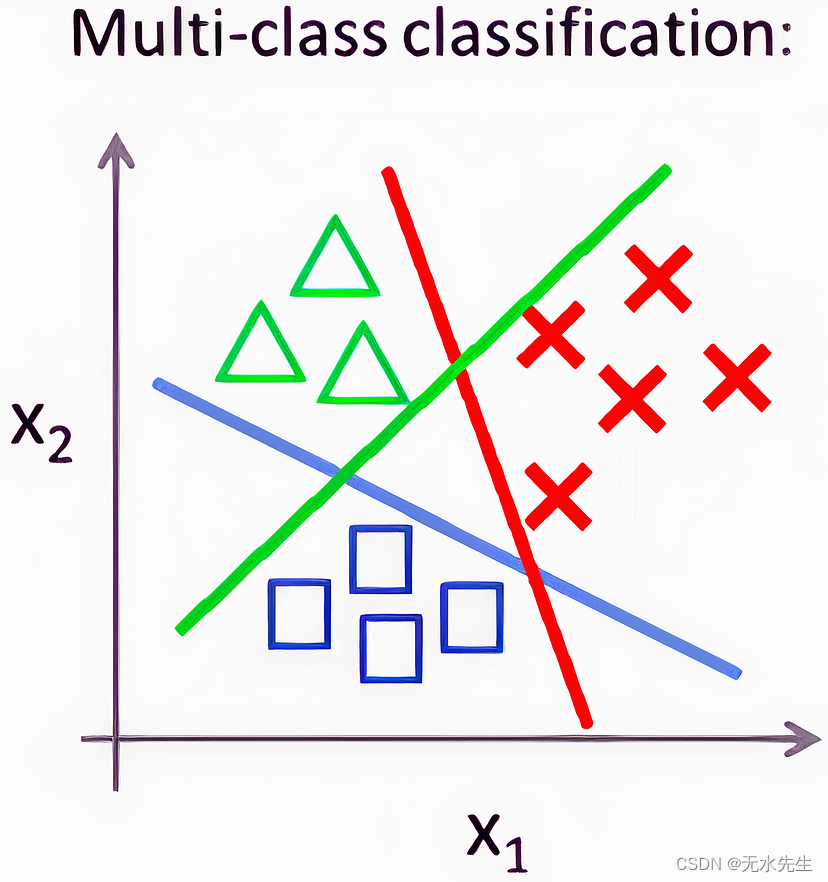
直观地说,我们似乎需要 3 个二元逻辑回归模型来解决这个问题,我们可以将它们组合在一起以制作多类逻辑回归模型。所以现在让我们定义这 3 个方程。
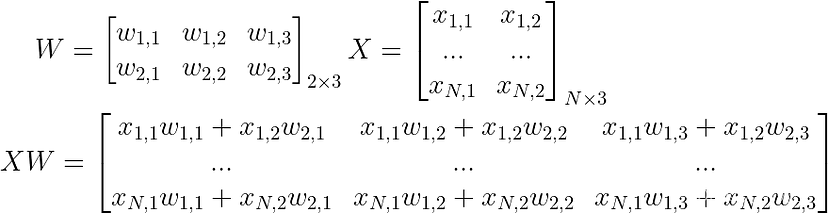
这里的错别字,X 是 Nx2
现在我们的权重不再是一个向量,而是一个矩阵。
通常,我们可以将 D 输入、K 类和 N 个样本的 X 和 W 视为
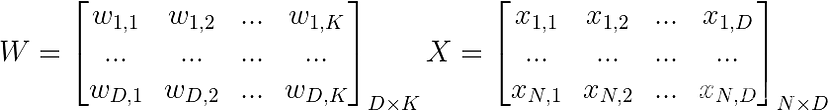
3.1 软最大激活
让我们继续以 K=3 为例,其中我们预测了 3 个类。现在我们需要一个与 sigmoid 不同的激活函数,如果我们使用 sigmoid,我们就不能再将其输出作为概率,因为它们的总和不会为 1。您可以通过设置随机权重并计算 3 个类的 sigmoid 来自行验证这一点。相反,让我们对 3 个神经元的输出进行归一化。为此,我们可以将每个neruon输出除以所有神经元输出的总和。为了确保所有输出都是绝对值,我们可以取所有输出的指数。类似于我们如何通过除以每个分量的大小来归一化线性代数中的向量。这样,每个神经元的每个输出都将是一个概率。我们可以简单地从所有神经元中获取最高概率作为我们的预测。
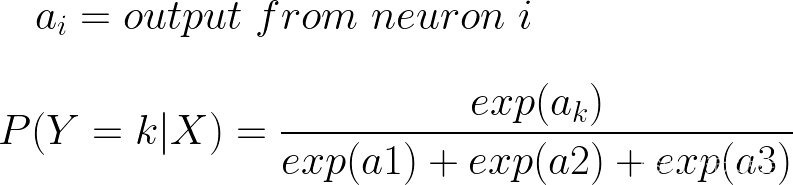
3.2 前向传递
让我们画一个图表,并做一个快速的例子来巩固所有这些。假设我们只有 1 个样本,让我们为权重矩阵分配随机权重。
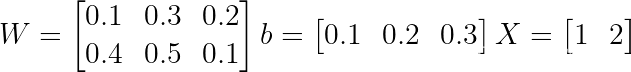
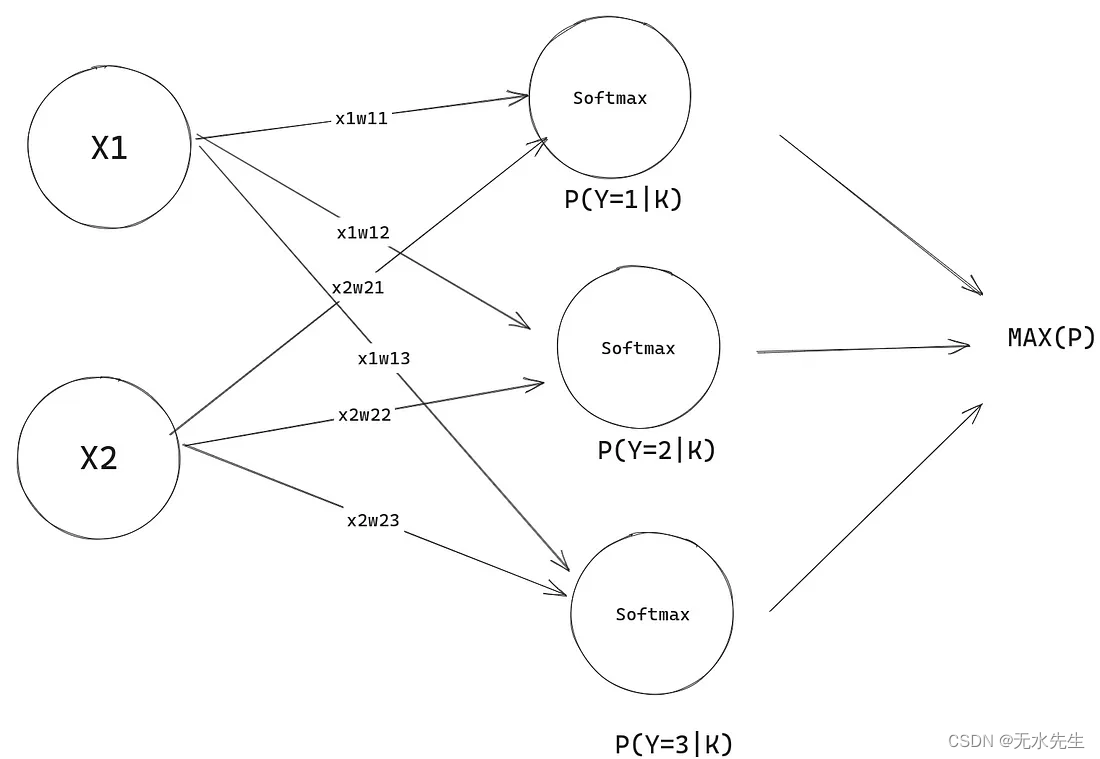
现在这实际上开始类似于神经网络,令人兴奋的是,这是一个没有隐藏层的神经网络。完成此操作后,我们将准备好处理神经网络。
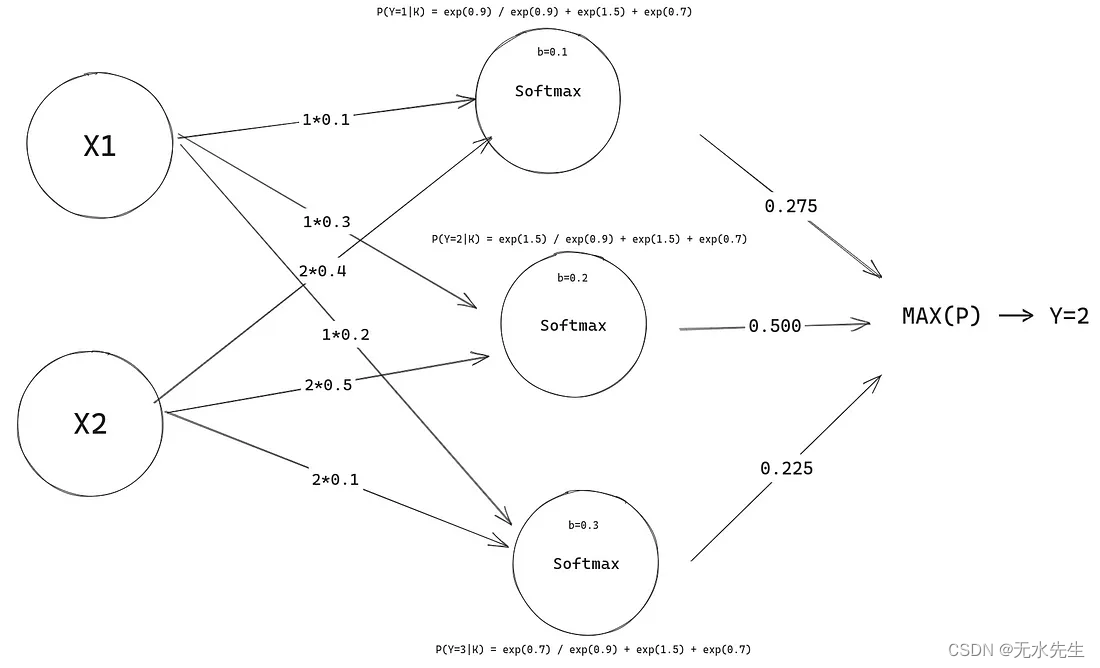
请注意所有概率的总和如何为 1 !
现在我们的模型可以做出预测,即使它们是完全随机的。
3.3 计算误差
我们需要弄清楚现在如何计算每个预测的误差。我们只关心模型应该预测的类的预测概率。单个样本的 Softmax 回归模型输出是一个大小为 NxK 的矩阵。我们可以对目标矩阵进行单热编码,从大小 Nx1 到大小 NxK。如果你不熟悉一种热门编码,我会在线性回归博客中介绍它。假设我们有 3 个目标,这些目标的表示将有一个热编码矩阵。

一般来说,这个独热编码矩阵的大小为 NxK,与我们的预测矩阵大小相同。然后我们可以对每个样本的所有 K 类求和并取交叉熵误差,如果该类不是目标,则误差将简单地乘以 0,因此我们只会得到目标类的模型预测的交叉熵误差,而忽略所有其他类。

在进行推导时携带负号是非常不方便的,所以让我们最大化对数可能性

3.4 练习:推导解决方案
如果你还没有学过矩阵微积分,你可能会在这里挣扎,但我建议你仍然遵循。如果您不熟悉,请观看此视频,了解如何将向量的导数转换为向量,因为我们将在推导中处理这个问题。将向量/矩阵的导数 wtr 转换为标量非常容易,我们已经完成了。
这个推导是相当棘手的,无论如何都不简单,所以在你完全理解它之前需要一些练习。我们想要采用的导数类似于我们对二进制逻辑回归所做的导数,只是现在变量略有不同。
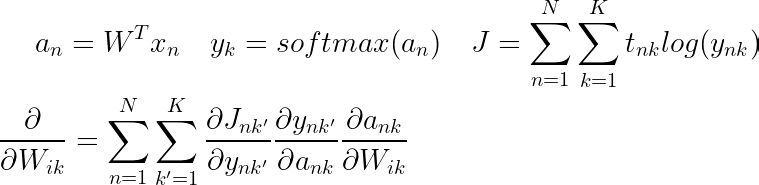
你会注意到这里有一些虚拟变量 n 和 k',在进行推导时,我们会变得非常混乱和模棱两可,我们将引用哪些索引,这就是我们使用这些虚拟变量的原因。你可以把这些变量想象成我们在 C 风格的 for 循环中用来迭代数组的变量。
这个衍生品链中的二阶导数是最困难的。这也是我们从k'切换到k的时候。我们从查看 k' 迭代的所有类切换到 k,即我们正在采用导数 wrt 的特定类。
发生这种情况的原因是 softmax 函数依赖于所有激活输入,而不仅仅是它自己的。因此,softmax 函数将向量作为输入。下面是一个 k=3 的快速示例。
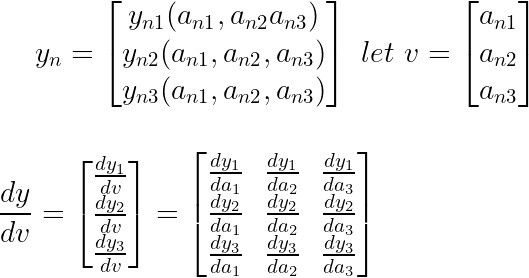
结果将是一个雅可比矩阵。
3.5 解决
Lets start by taking the first derivative
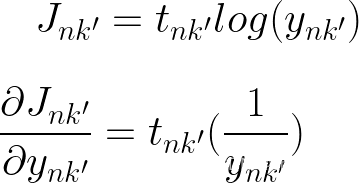
现在是第二个也是最难的导数,在我们采用导数之前,让我们快速回顾一下我们正在处理的内容
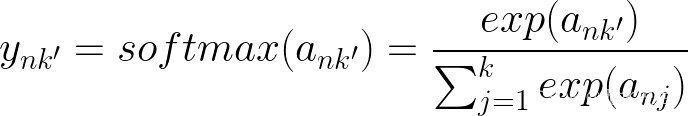
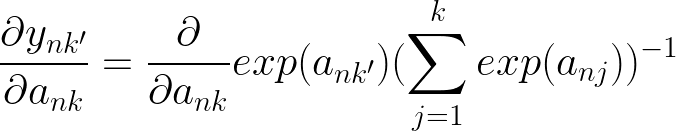
当 k != k' 和 k = k' 时,我们有 2 种不同的情况,因为我们取导数 wrt ank,当 k != k' 时,我们将 ank' 项视为常数,当它们相等时,我们还必须取它的导数。同样对于求和,我们必须考虑 j=k 何时并取相应的导数。
让我们首先考虑当 k != k'
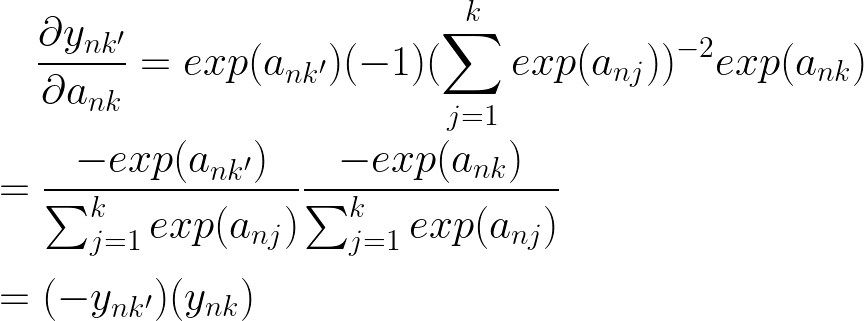
现在让我们考虑当 k = k'
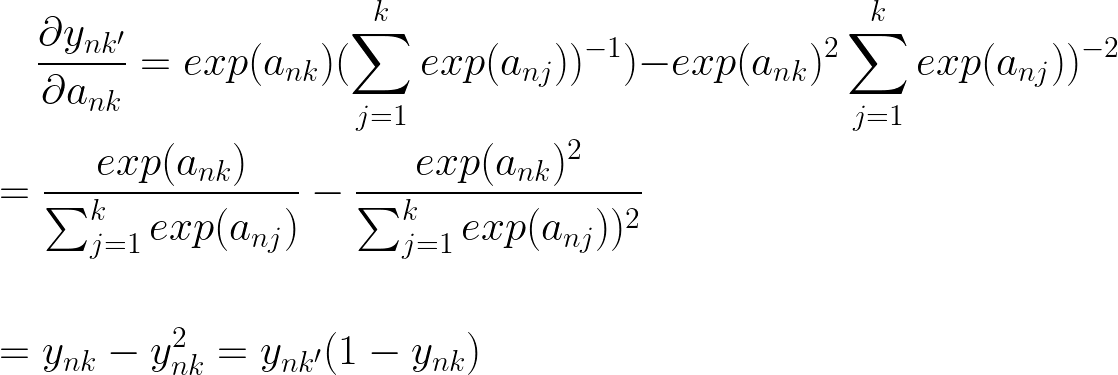
我们可以使用克罗内克三角洲函数来处理我们需要值等于 0 或 1 的情况。
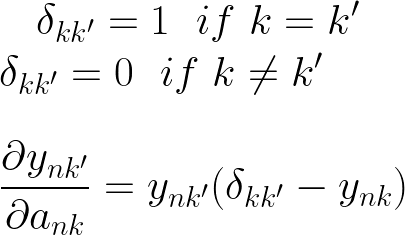
当 k = k' 时,我在导数的最终结果中用 ynk 代替了 ynk',这样我们就可以有一个简洁的最终表达式来总结这两种情况。
现在我们可以进入第三阶也是最后一阶导数
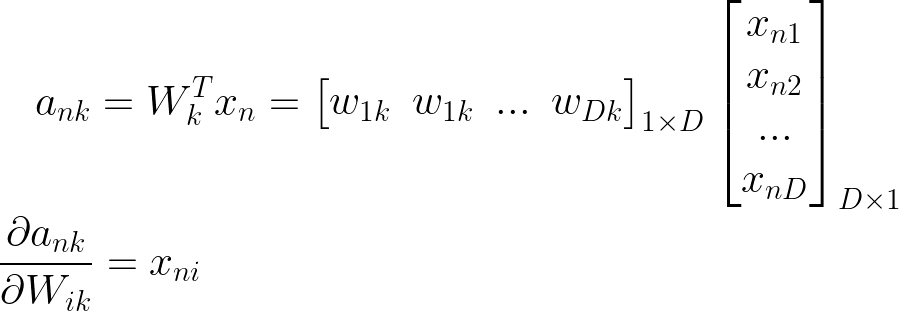
将所有三个导数组合在一起,我们得到
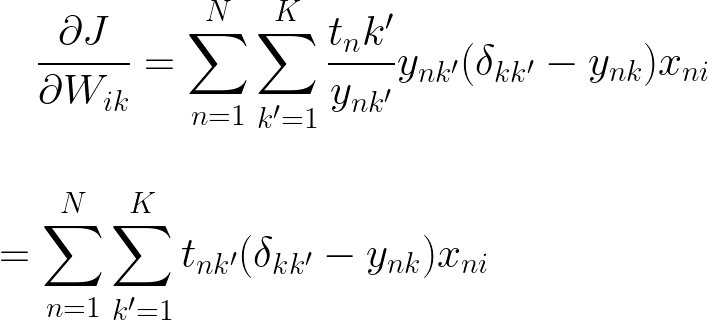
现在为了隔离增量,让我们暂时忘记 N 上的求和并扩展表达式
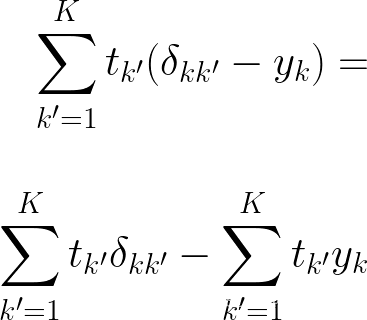
我们知道克罗内克增量 = 1 当且仅当 k = k',所以我们知道整个三角洲的总和将乘以零,除非 k = k'
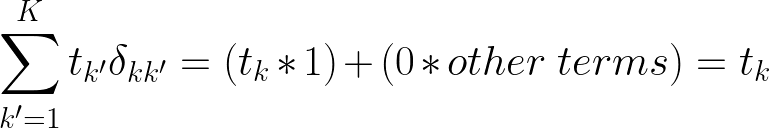
由于 yk 不依赖于求和,我们可以将其分解掉,并且所有 k 可能性中只有 1 个目标,因此我们知道 tk' = 1 的总和
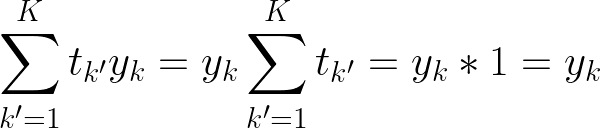
现在让我们回到 N 上的求和。
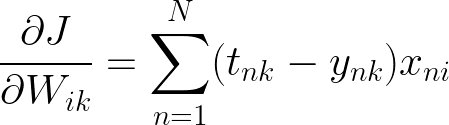
这个结果看起来与二进制逻辑回归解决方案非常相似,这很好。
四、结论
您可以尝试自己编写 Softmax 回归算法,我之所以不在这里编码,是因为我们将在下一篇博客中做神经网络时深入探讨它。如果我在这里共享非常相似的代码,它只会变得多余。我们在这里学到的想法将成为神经网络的完美垫脚石,如果你很好地理解了Logisitic Regressoin,它将使神经网络变得更容易。我在这个博客中没有涉及很多东西,比如正则化和其他实际问题。将此视为简要介绍,而不是全面的指南。祝你好运!
相关文章:
从头开始机器学习:逻辑回归
一、说明 本篇实现线性回归的先决知识是:基本线性代数,微积分(偏导数)、梯度和、Python (NumPy);从线性方程入手,逐渐理解线性回归预测问题。 二、逻辑回归简介 我们将以我们在线性回…...

插入排序 算法
从第二个开始,从后面往前找,如果比其小,就交换,else 就终止 for i 1 i <n i for j i j > 0 (到第二个) j-- if < swap 下面给出源码 //对插入排序来说,直接从第二个元素开始template<ty…...
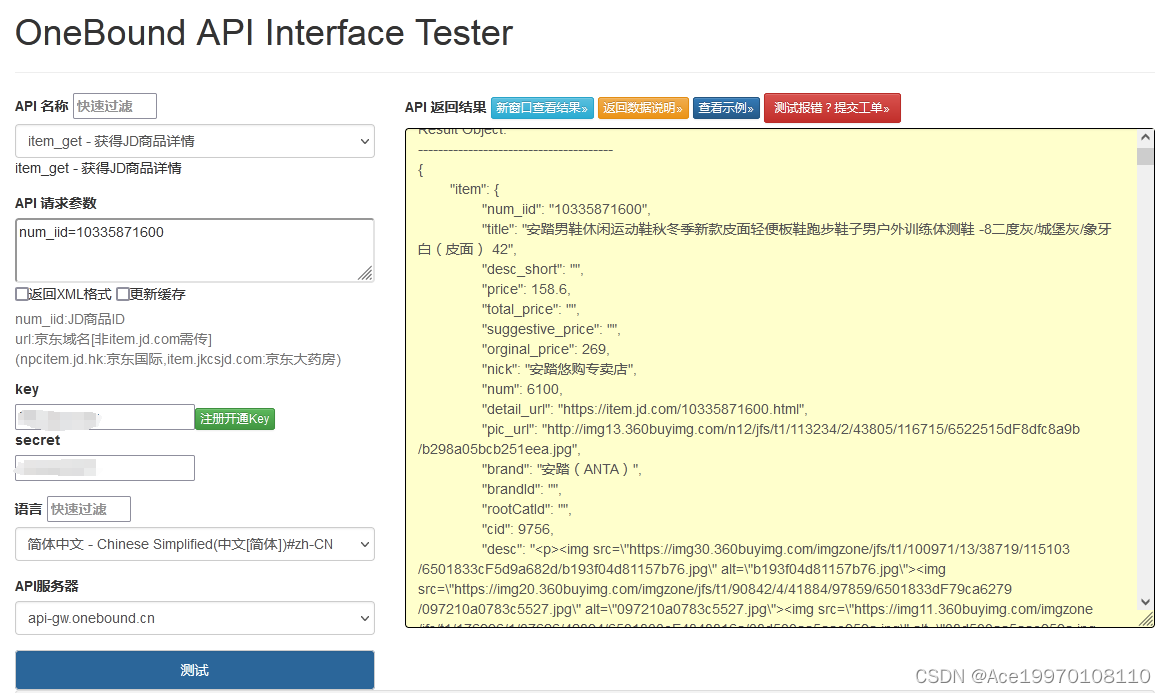
“揭秘!如何通过京东商品详情接口轻松获取海量精准商品信息!“
京东商品详情接口可以通过HTTP GET请求获取商品详情信息。 请求参数包括num_iid,表示JD商品ID。 请求示例: GET /jd/item_get/?num_iid10335871600 HTTP/1.1 Host: api-vx.Taobaoapi2014.cn Connection: close Accept-Encoding: gzip 点击获取…...

已经有多人中招,不要被AI换脸技术骗了!
您好,我是码农飞哥(wei158556),感谢您阅读本文,欢迎一键三连哦。 💪🏻 1. Python基础专栏,基础知识一网打尽,9.9元买不了吃亏,买不了上当。 Python从入门到精…...

solidworks 2024新功能之--保存为低版本 硕迪科技
大家期盼已久的SOLIDWORKS保存低版本文件功能来了,从SOLIDWORKS 2024 开始,您可以将在最新版本的SOLIDWORKS 中创建的SOLIDWORKS零件、装配体和工程图另存为SOLIDWORKS 早期版本的全功能文档(完成的特征树与相关参数)。 将文件另…...
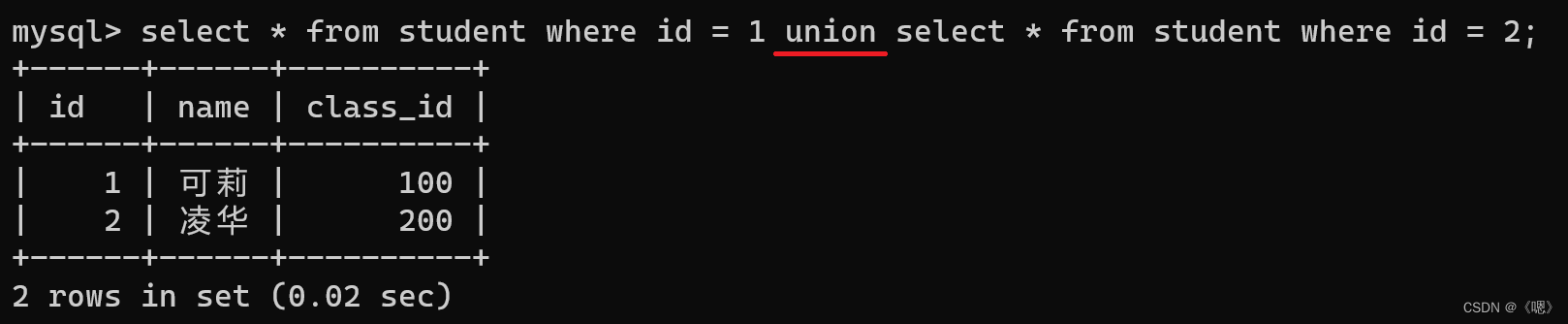
MySQL --- 聚合查询 和 联合查询
聚合查询: 下文中的所有聚合查询的示例操作都是基于此表: 聚合函数 聚合函数都是行与行之间的运算。 count() select count(列名) from 表名; 统计该表中该列的行数,但是 null 值不会统计在内,但是如果写为 count(*) 那么 nu…...
Note——torch.size() umr_maximum() array.max() itertools.product()
torch.size Problem TypeError: ‘torch.Size’ object is not callable Reason Analysis torch.Size函数不可调用 因为torch只可以.size() 或 shape Solution 将y.shape()替换为y.size() 或 y.shape ytorch.normal(0,0.01,y.size())2 return umr_maximum(a, axis, None…...

python学习笔记6-DefaultDict
对于一般的字典来说,如果键不存在会导致【KeyError】,因此可以考虑用DefaultDict # Defining the dict d defaultdict(def_value) d["a"] 1 d["b"] 2print(d["a"]) print(d["b"]) print(d["c"…...

Redis 底层对 String 的 3 个优化
Redis对 String 类型实现了很多优化,通过以下三个重要的优化点来解释: 1. 简单动态字符串(SDS) Redis 的 String 类型内部采用简单动态字符串(SDS)来管理字符串。相比于 C 语言的原生字符串,S…...
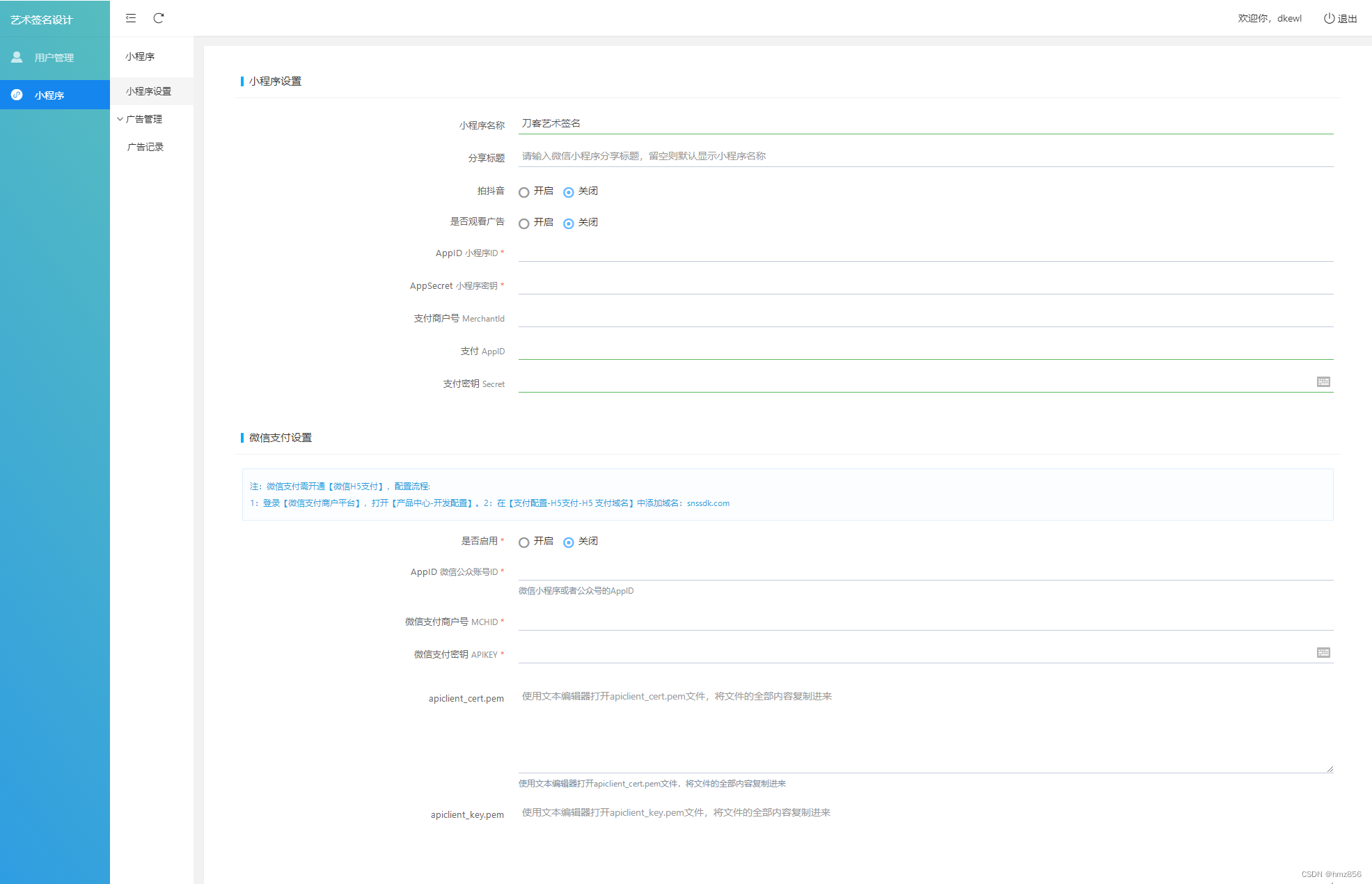
简约艺术签名小程序源码/流量主小程序源码/字节跳动抖音小程序
源码简介: 本源码为简约艺术签名小程序、流量主小程序以及字节跳动抖音小程序的源代码。该小程序是一款实用的工具,旨在帮助用户创建各种独特的艺术签名,以便在社交媒体平台上更好地展示用户的个性和创意。 源码链接: 网盘源码 …...
挂载iso文件和配置apt本地源)
Ubuntu(kylin)挂载iso文件和配置apt本地源
版本说明:Ubuntu Server 16.04 LTS解决问题:解决在无任何互联网的环境下,安装软件时缺少依赖包的问题 方法一:通过虚拟机挂载 将镜像挂载到虚拟机以VMware Workstation为例,打开“虚拟机设置”,点击“CD/DVD”选项,将 “设备状态”中的“<...

wps表格求标准差怎么算?
在WPS表格中,要计算标准差,可以使用STDEV函数。标准差是一种衡量数据集合离散程度的统计指标。下面我将详细介绍如何使用STDEV函数来计算标准差。 STDEV函数的语法为:STDEV(range) 其中,range表示要计算标准差的数据范围&#x…...

安达发|制造企业生产排产现状和APS系统的解决方案
随着市场竞争的加剧,制造业企业面临着生产效率、成本控制和客户满意度等方面的巟大压力。在这种背景下,生产排产作为制造业的核心环节,对企业的生产经营具有重要意义。本文将针对制造业的生产排产现状进行分析,并提出相应的APS系统…...
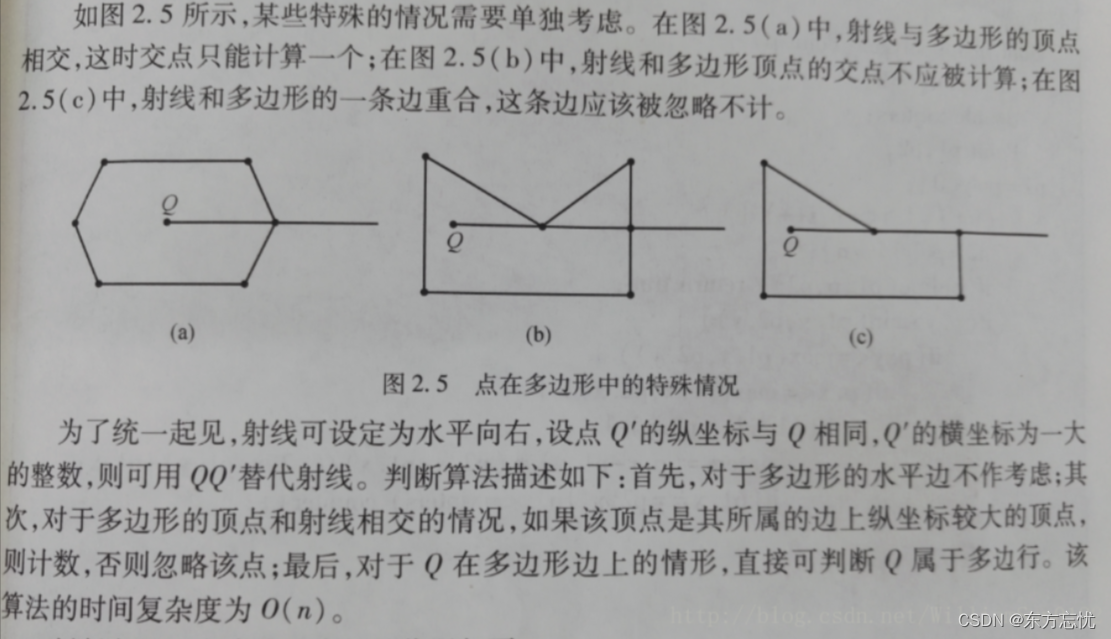
Qt判断一个点在多边形内还是外(支持凸边形和凹变形)
这里实现的方法是转载于https://blog.csdn.net/trj14/article/details/43190653和https://blog.csdn.net/WilliamSun0122/article/details/77994526 来实现的,并且按照Qt的规则进行了调整。 以下实现方法有四种,每种方法的具体讲解在转载的博客中有说明&…...

MySQL导入数据库出现 Got error 168 from storage engine错误
“Got error 168 from storage engine” 是 MySQL 数据库的一个错误,通常是由于存储引擎发生了一些问题导致的。这个错误可能有多种原因引起。以下是一些可能的解决方法: 检查硬盘空间:确保目标数据库的服务器有足够的硬盘空间来执行导入操作…...
使用 VS Code 作为 VC6 的编辑器
使用 VS Code 作为 VC 6.0 的编辑器 由于一些众所周知的原因,我们不得不使用经典(过时)的比我们年龄还大的已有 25 年历史的 VC 6.0 来学习 C 语言。而对于现在来说,这个经典的 IDE 过于简陋,并且早已不兼容新的操作系…...

Peter算法小课堂—蠕动区间
蠕动区间 蠕动区间(尺取法、双游标)是一个经典的优化算法。 我们以毛毛虫🐛举例说明 具体的,我们看题目 例题 最小区间 这一题,我们用暴力法,复杂度O(N^2) 先给出暴力法代码 int ansn1; for(int tail…...
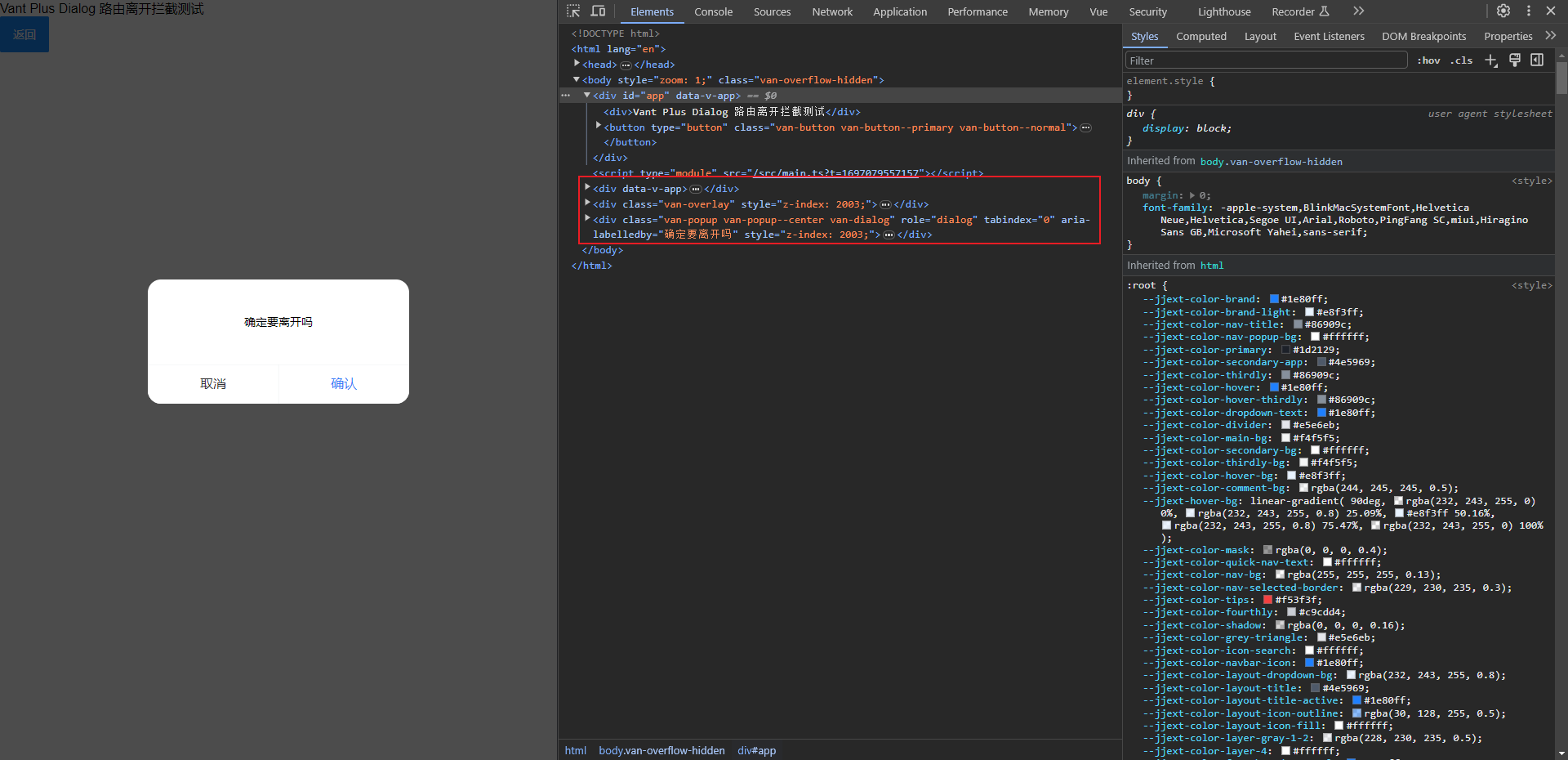
Vant和ElementPlus在vue的hash模式的路由下路由离开拦截使用Dialog和MessageBox失效
问题复现 ElementPlus:当点击返回或者地址栏回退时,MessageBox无效 <template><div>Element Plus Dialog 路由离开拦截测试</div><el-button type"primary" click"$router.back()">返回</el-button>…...

上海市通过区块链技术攻关 构建数字经济可信安全技术底座
日前,上海市印发《上海区块链关键技术攻关专项行动方案(2023—2025年)》(以下简称《行动方案》),提出到2025年,在区块链体系安全、密码算法等基础理论以及区块链专用处理器、智能合约、跨链、新…...

Java 面试题
昨天面试了两个Java开发程序员,问了一些问题,回答的不是很好,看看大家的回答如何,可以在评论区回复,测试下自己的水平。 A程序员: 1. 自我介绍一下; 2. 企业级和互联网行业都有那些项目经验,简…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
