Qt判断一个点在多边形内还是外(支持凸边形和凹变形)
这里实现的方法是转载于https://blog.csdn.net/trj14/article/details/43190653和https://blog.csdn.net/WilliamSun0122/article/details/77994526
来实现的,并且按照Qt的规则进行了调整。
以下实现方法有四种,每种方法的具体讲解在转载的博客中有说明,这里不做重复阐述。
这里只说下代码的具体实现和每种方法的时间复杂度。
强烈推荐第一种方法,其它三种针对一些特殊图形或多或少都有一些问题。
方法一:射线法
时间复杂度:O(n) 。
适用范围:任意多边形。
优点:不需考虑精度误差和多边形点给出的顺序。
算法思想:以被测点Q为端点,向任意方向作射线(一般水平向右作射线),统计该射线与多边形的交点数。如果为奇数,Q在多边形内;如果为偶数,Q在多边形外。计数的时候会有一些特殊情况,如图
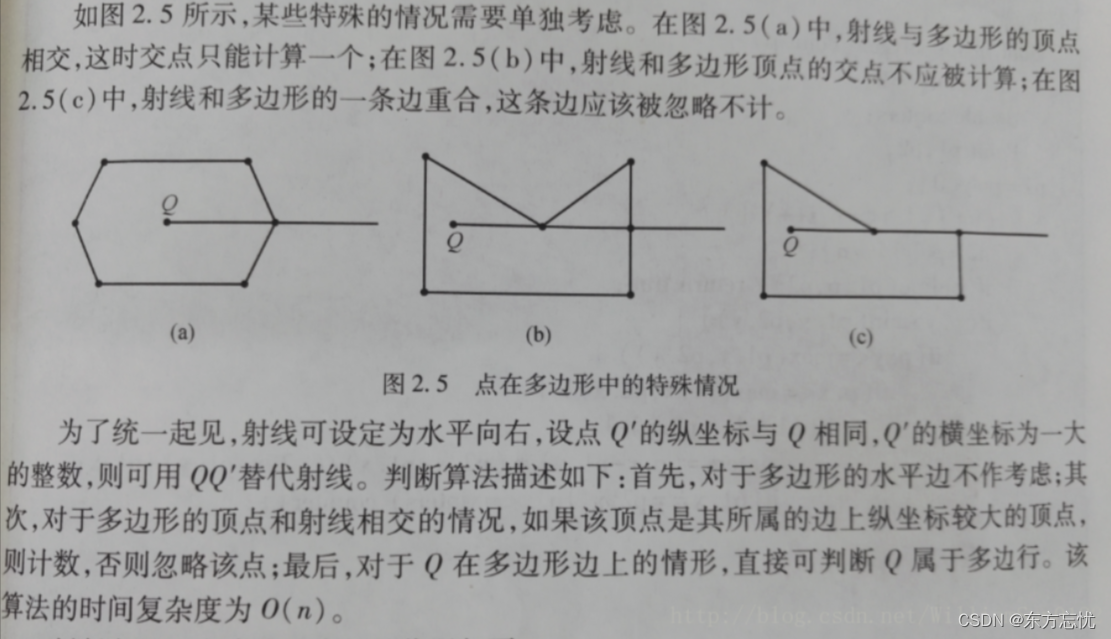
//判断点P在多边形内-射线法
bool Widget::InsidePolygon( QVector<QPointF> polygon,QPointF pt )
{int i,j;bool inside,redo;int N = polygon.size();redo = true;for (i = 0;i < N;++i){// 是否在顶点上if (polygon[i].x() == pt.x() && polygon[i].y() == pt.y()){redo = false;inside = true;break;}}while (redo){redo = false;inside = false;for (i = 0,j = N - 1;i < N;j = i++){if ( (polygon[i].y() < pt.y() && pt.y() < polygon[j].y()) ||(polygon[j].y() < pt.y() && pt.y() < polygon[i].y()) ){if (pt.x() <= polygon[i].x() || pt.x() <= polygon[j].x()){double _x = (pt.y()-polygon[i].y())*(polygon[j].x()-polygon[i].x())/(polygon[j].y()-polygon[i].y())+polygon[i].x();if (pt.x() < _x) // 在线的左侧inside = !inside;else if (pt.x() == _x) // 在线上{inside = true;break;}}}else if ( pt.y() == polygon[i].y()){if (pt.x() < polygon[i].x()) // 交点在顶点上{if (polygon[i].y() > polygon[j].y())pt.setY(pt.y() - 1);elsept.setY(pt.y() + 1);redo = true;break;}}else if ( polygon[i].y() == polygon[j].y() && pt.y() == polygon[i].y() &&((polygon[i].x() < pt.x() && pt.x() < polygon[j].x()) ||(polygon[j].x() < pt.x() && pt.x() < polygon[i].x())) )// 在水平的边界线上{inside = true;break;}}}return inside;
}方法二:面积和判别法
时间复杂度:大于O(n)。
适用范围:所有凸边形,部分凹变形。
优点:算法简单。
缺点:有精度要求,强调多边形点给出的方向(逆时针)。
算法思想:如果点在多边形内部或者边上,那么点与多边形所有边组成的三角形面积和等于多边形面积。多边形的面积可以用叉积计算即连接坐标原点和各顶点形成向量,所有向量叉积的0.5的和即为多边形面积。不过计算面积是会有一定误差的,需要设置精度的误差范围。
//面积和判别法
bool InsidePolygon3( QVector<QPointF> polygon,QPointF pt )
{int i,j;bool inside = false;double polygon_area = 0;double trigon_area = 0;int N = polygon.size();for (i = 0,j = N - 1;i < N;j = i++){polygon_area += polygon[i].x() * polygon[j].y() - polygon[j].x() * polygon[i].y();trigon_area += abs(pt.x() * polygon[i].y() -pt.x() * polygon[j].y() -polygon[i].x() * pt.y() +polygon[i].x() * polygon[j].y() +polygon[j].x() * pt.y() -polygon[j].x() * polygon[i].y());}trigon_area *= 0.5;polygon_area = abs(polygon_area * 0.5);if ( fabs(trigon_area - polygon_area) < 1e-7 )inside = true;return inside;
}
方法三:点线判别法
时间复杂度:O(n)。
适用范围:所有凸边形,部分凹变形。
算法思想:对于多边形(正向,即逆时针),如果一个点它的所有有向边的左边,那么这个点一定在多边形内部。利用叉积正好可以判断点与给定边的关系,即点是在边的左边右边还是边上。
//点线判别法
bool InsidePolygon4( QVector<QPointF> polygon,QPointF p )
{int i,j;bool inside = false;int count1 = 0;int count2 = 0;int N = polygon.size();for (i = 0,j = N - 1;i < N;j = i++){double value = (p.x() - polygon[j].x()) * (polygon[i].y() - polygon[j].y()) - (p.y() - polygon[j].y()) * (polygon[i].x() - polygon[j].x());if (value > 0)++count1;else if (value < 0)++count2;}if (0 == count1 ||0 == count2){inside = true;}return inside;
}
方法四:角度和判别法
时间复杂度:O(n)。
适用范围:所有凸边形,部分凹变形。
优点:不强调多边形点给出顺序。
缺点:这个算法对精度的要求很高(会造成很大精度误差)。
算法思想:连接被测点与多边形所有顶点所形成的所有角的角度和在精度范围内等于则该点在多边形内,否则在多边形外。
// 根据需要不判断顶点
bool IsPointInLine( QPointF &pt,QPointF &pt1,QPointF &pt2 )
{bool inside = false;if (pt.y() == pt1.y() &&pt1.y() == pt2.y() &&((pt1.x() < pt.x() && pt.x() < pt2.x()) ||(pt2.x() < pt.x() && pt.x() < pt1.x())) ){inside = true;}else if (pt.x() == pt1.x() &&pt1.x() == pt2.x() &&((pt1.y() < pt.y() && pt.y() < pt2.y()) ||(pt2.y() < pt.y() && pt.y() < pt1.y())) ){inside = true;}else if ( ((pt1.y() < pt.y() && pt.y() < pt2.y()) ||(pt2.y() < pt.y() && pt.y() < pt1.y())) &&((pt1.x() < pt.x() && pt.x() < pt2.x()) ||(pt2.x() < pt.x() && pt.x() < pt1.x())) ){if (0 == (pt.y()-pt1.y())/(pt2.y()-pt1.y())-(pt.x() - pt1.x()) / (pt2.x()-pt1.x())){inside = true;}}return inside;
}//角度和判别法
bool InsidePolygon2( QVector<QPointF> polygon,QPointF p)
{int i,j;double angle = 0;bool inside = false;int N = polygon.size();for (i = 0,j = N - 1;i < N;j = i++){if (polygon[i].x() == p.x() && // 是否在顶点上polygon[i].y() == p.y()){inside = true;break;}else if (IsPointInLine(p,polygon[i],polygon[j])) // 是否在边界线上{inside = true;break;}double x1,y1,x2,y2;x1 = polygon[i].x() - p.x();y1 = polygon[i].y() - p.y();x2 = polygon[j].x() - p.x();y2 = polygon[j].y() - p.y();double radian = atan2(y1,x1) - atan2(y2,x2);radian = abs(radian);if (radian > M_PI) radian = 2* M_PI - radian;angle += radian; // 计算角度和}if ( fabs(6.28318530717958647692 - angle) < 1e-7 )inside = true;return inside;
}相关文章:

Qt判断一个点在多边形内还是外(支持凸边形和凹变形)
这里实现的方法是转载于https://blog.csdn.net/trj14/article/details/43190653和https://blog.csdn.net/WilliamSun0122/article/details/77994526 来实现的,并且按照Qt的规则进行了调整。 以下实现方法有四种,每种方法的具体讲解在转载的博客中有说明&…...

MySQL导入数据库出现 Got error 168 from storage engine错误
“Got error 168 from storage engine” 是 MySQL 数据库的一个错误,通常是由于存储引擎发生了一些问题导致的。这个错误可能有多种原因引起。以下是一些可能的解决方法: 检查硬盘空间:确保目标数据库的服务器有足够的硬盘空间来执行导入操作…...
使用 VS Code 作为 VC6 的编辑器
使用 VS Code 作为 VC 6.0 的编辑器 由于一些众所周知的原因,我们不得不使用经典(过时)的比我们年龄还大的已有 25 年历史的 VC 6.0 来学习 C 语言。而对于现在来说,这个经典的 IDE 过于简陋,并且早已不兼容新的操作系…...

Peter算法小课堂—蠕动区间
蠕动区间 蠕动区间(尺取法、双游标)是一个经典的优化算法。 我们以毛毛虫🐛举例说明 具体的,我们看题目 例题 最小区间 这一题,我们用暴力法,复杂度O(N^2) 先给出暴力法代码 int ansn1; for(int tail…...
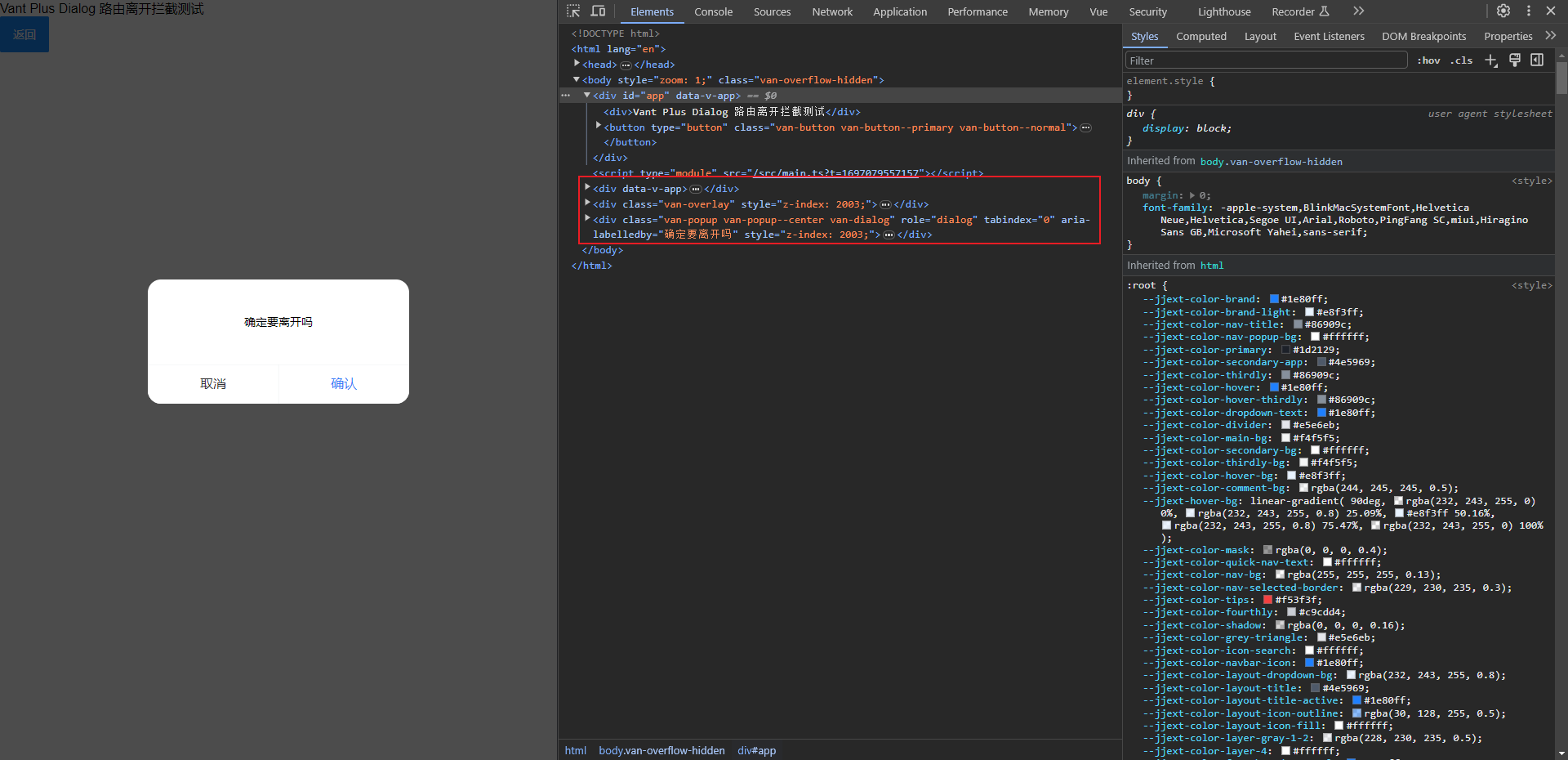
Vant和ElementPlus在vue的hash模式的路由下路由离开拦截使用Dialog和MessageBox失效
问题复现 ElementPlus:当点击返回或者地址栏回退时,MessageBox无效 <template><div>Element Plus Dialog 路由离开拦截测试</div><el-button type"primary" click"$router.back()">返回</el-button>…...

上海市通过区块链技术攻关 构建数字经济可信安全技术底座
日前,上海市印发《上海区块链关键技术攻关专项行动方案(2023—2025年)》(以下简称《行动方案》),提出到2025年,在区块链体系安全、密码算法等基础理论以及区块链专用处理器、智能合约、跨链、新…...

Java 面试题
昨天面试了两个Java开发程序员,问了一些问题,回答的不是很好,看看大家的回答如何,可以在评论区回复,测试下自己的水平。 A程序员: 1. 自我介绍一下; 2. 企业级和互联网行业都有那些项目经验,简…...
layui 表格 展开
一、表格嵌套表格(手风琴打开) <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>设备上下线统计</title><script type"text/javascript" src"../../../l…...
[尚硅谷React笔记]——第4章 React ajax
目录: 脚手架配置代理_方法一 server1.js开启服务器server1:App.js解决跨域问题:脚手架配置代理_方法二 server2.js开启服务器server2第一步:创建代理配置文件编写setupProxy.js配置具体代理规则:App.js运行结果&a…...

Richard Stallman 正在与癌症作战
导读为了纪念 GNU 项目成立 40 周年,自由软件基金会(FSF)已计划在 10 月 1 日(即GNU 40)为家庭、学生以及美国的其他人群组织一场黑客马拉松活动。 活动之前,GNU 项目于 9 月 27 日迎来了 40 岁生日&#…...

MathType7.4最新免费版(公式编辑器)下载安装包附安装教程
MathType是一款专业的数学公式编辑器,理科生专用的必备工具,可应用于教育教学、科研机构、工程学、论文写作、期刊排版、编辑理科试卷等领域。可视化公式编辑器轻松创建数学方程式和化学公式。兼容Office Word、PowerPoint、Pages、Keynote、Numbers 等7…...

如何支持h.265视频
前言 略 h.265视频 h.265是一种视频编码格式。 随着视频编码技术的发展,相比H.264, H.265同等画质体积仅为一半、带宽占用省一半、画质更细腻等诸多优势。 但Web浏览器还不支持H.265的解码播放,因此基于Web Assembly(封装FFmpeg)、JS解封装、Canvas投…...
)
vue 放大镜(简易)
目录 zoom组件 <template><div class"pic-img"><div class"img-container"><img ref"img" load"imgLoaded" :src"url" :style"overlayStyle" error"imgerrorfun"/><div cl…...

【计算机网络】第一章——概述
个人主页直达:小白不是程序媛 系列专栏:计算机网络基础 目录 前言 计算机网络概述 概念 功能 组成 分类 标准化工作 性能指标 速率 带宽 吞吐量 时延 时延带宽积 往返时延RTT 利用率 分层 为什么要分层? 分层的基本原则&am…...

vue实现在页面拖拽放大缩小div并显示鼠标在div的坐标
1、功能要求: 实现在一个指定区域拖拽div,并可以放大缩小,同时显示鼠标在该div里的坐标,如图可示 缩小并拖动 2、实现 <div class"div_content" ref"div_content"><div class"div_image" id"…...
-- io - io操作(扩展))
LuatOS-SOC接口文档(air780E)-- io - io操作(扩展)
示例 -- io模块是lua原生模块,LuatOS增加了一些API -- 请配合os模块一起使用-- 只读模式, 打开文件 local fd io.open("/xxx.txt", "rb") -- 读写默认,打开文件 local fd io.open("/xxx.txt", "wb") -- 写入文件,且截断为0字节 loc…...
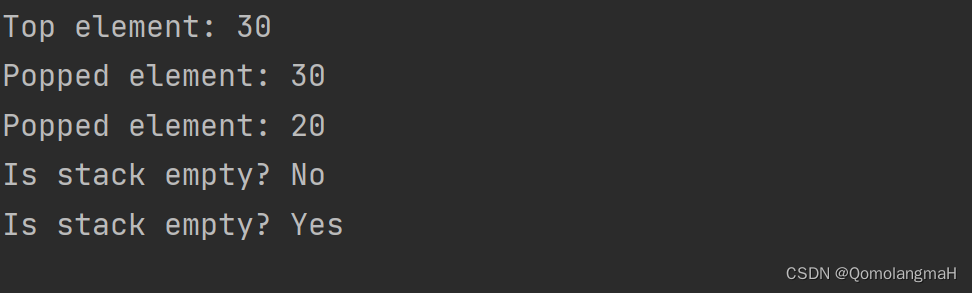
【数据结构】线性表(六)堆栈:顺序栈及其基本操作(初始化、判空、判满、入栈、出栈、存取栈顶元素、清空栈)
文章目录 一、堆栈1. 定义2. 基本操作 二、顺序栈0. 顺序表1. 头文件和常量2. 栈结构体3. 栈的初始化4. 判断栈是否为空5. 判断栈是否已满6. 入栈7. 出栈8. 查看栈顶元素9. 清空栈10. 主函数11. 代码整合 堆栈Stack 和 队列Queue是两种非常重要的数据结构,两者都是特…...

父组件可以监听到子组件的生命周期吗?
在 Vue 中,父组件是可以监听到子组件的生命周期的。Vue 提供了一些特殊的钩子函数,可以在父组件中监听子组件的生命周期事件。 以下是一些常用的方法来监听子组件的生命周期: 1:使用$emit: 在子组件的生命周期钩子函数中,使用 $emit 方法触发自定义事件,向父组件发送通…...
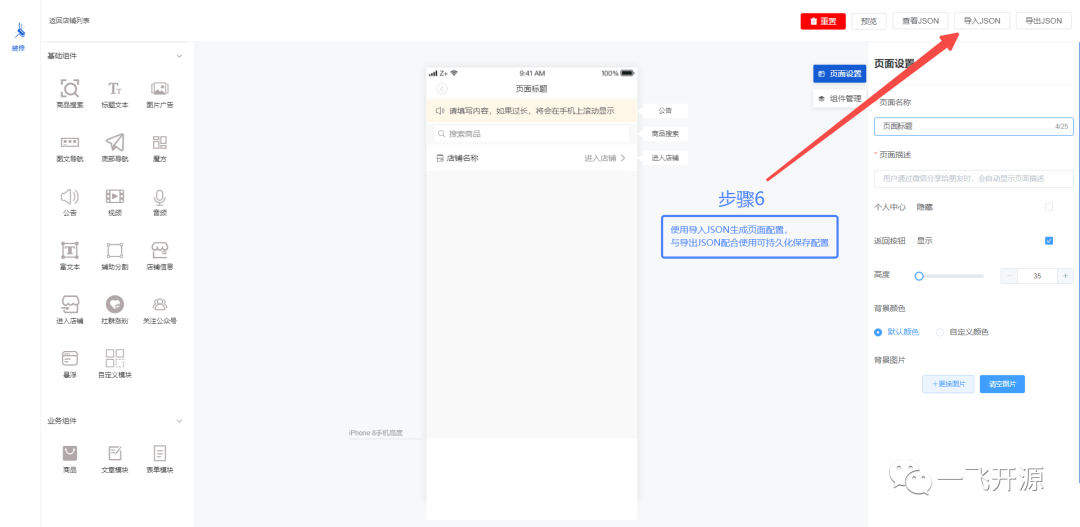
[开源]MIT开源协议,基于Vue3.x可视化拖拽编辑,页面生成工具
一、开源项目简介 AS-Editor 基于 Vue3.x 可视化拖拽编辑,页面生成工具。提升前端开发效率,可集成至移动端项目作为通过定义 JSON 直接生成 UI 界面。 二、开源协议 使用MIT开源协议 三、界面展示 四、功能概述 基于Vue可视化拖拽编辑,…...

【C++ Primer Plus学习记录】数组的替代品
目录 1.模板类vector 2.模板类array(C11) 3.比较数组、vector对象和array对象 模板类vector和array是数组的替代品。 1.模板类vector 模板类vector类似于string类,也是一种动态数组。您可以在运行阶段设置vector对象的长度,可…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
